
JDLAが主催するG検定では、ディープラーニング以外の機械学習手法に関する設問も出題されます。ここでは、主な機械学習手法の全般を体系的にまとめることで検定対策を行います。
こんにちは。wat(@watlablog)です。G検定の学習ノート!ここではディープラーニング以外の機械学習手法全般をまとめます!
本ブログで学習結果を記録し、結果としてG検定に合格しました!皆さんも是非当ブログを参考にして下さい。

G検定に必要な知識
G検定学習のシラバスと本記事でまとめる内容
G検定とは、日本ディープラーニング協会(JDLA:Japan Deep Learning Association)が主催している認定試験です。
JDLA公式ページ:https://www.jdla.org/
G検定の概要は前の記事「【G検定の学習】人工知能(AI)の定義と分類を整理!」に記載していますので、最初から読みたい!という方は是非リンクをクリックしてみて下さい。
G検定の出題範囲はJDLAから「学習のシラバス」として公開されています。
この記事ではシラバスに記載されている「機械学習の具体的な手法」をまとめています。
JDLAは日本ディープラーニング協会という名前の通り、ディープラーニング技術の普及を目的とした協会ですが、G検定にはディープラーニング以外の機械学習に関する設問が多く出題されます。
このページは「ディープラーニング以外の機械学習ってどんな種類があって、どんな特徴があるのか」という疑問を解決します。
参考書
僕の学習は「徹底攻略 ディープラーニングG検定ジェネラリスト問題集」で設問を解き、わからないことをWebやその他書籍で調べるというスタイルです。
※2022年2月はこちらの第2版が最新のようですのでリンクを更新しました。
本記事でまとめている内容は一般的な機械学習アルゴリズムの概要やその特徴です。
著作権の関係上、本に記載されているような設問はここに載せることができませんが、G検定を受験する予定のある方は、当ブログ等で学習した実力確認として上記問題集を購入してみると良いかも知れません。
それでは早速説明していきます!
既にいくつかの知識をお持ちの方は、上にある目次から必要な所へジャンプしてみて下さい!
最低限知っておきたい機械学習の基礎知識
学習の分類:教師あり学習/教師なし学習/強化学習

機械学習の手法には、教師あり学習と教師なし学習、または強化学習という方法があります。
教師あり学習
教師あり学習(Supervised learning)とは、正解のわかっているデータを用いて学習を行うことで、未知の値を予測する学習方法です。
教師あり学習で解決する主な問題には分類問題と回帰問題があります。
分類問題(下図左)は未知のデータがどのクラス(ネコかイヌか、乗り物か否か…といった属性・括りをクラスと呼ぶ)になるかを予測する問題で、回帰問題(下図右)は未知のデータの出力値がいくつになるかを予測する問題のことを意味します。
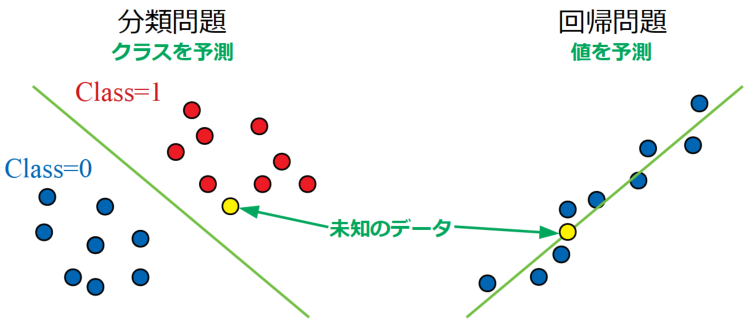
いずれも正解となる教師データを目標にフィッティングする工程を持つことが特徴です。
このページで後程紹介するほとんどの方法はこの教師あり学習に分類することができます。
教師なし学習
教師なし学習(Unsupervised learning)とは、正解の用意されていない状況でデータのみが与えられ、データの持つ本質的な構造を抽出するための学習手法です。
教師なし学習の代表的な手法には、データがどのようなクラスタ(まとまり)になっているかを抽出するクラスタリングやデータの情報を極力失わないように次元を削減する主成分分析等の手法があります。
強化学習
強化学習(Reinforcement learning)とは、エージェントと呼ばれるプレイヤー自身が現在の状態から行動を選択し、収益を最大化させるような方策を学習する手法のことです。
プレイヤーという言葉はチェスや囲碁といったゲームAIという意味合いで使われることが多くあります。ここで、方策とはエージェントがある状態の時にどういった行動をとれば良いかを示す関数です。
学習データの前処理

標準化/正規化/正則化
機械学習をするためにはデータが必要不可欠ですが、データは何でも良いわけではなく、これから使用する機械学習アルゴリズムに適した形にするための前処理(Preprocessing)が必要です。
データの前処理として重要な事項に標準化と正規化があります。
標準化(Standardization)はデータに対し「平均を0に、標準偏差を1にする」という加工を行い、正規化(Normalization)はスケーリングに代表されるように「データを一定の規則に従って加工し、扱いやすくする」加工のことを意味します。
標準化と正規化については「Python/sklearnで学習データの前処理!標準化と正規化」という記事でPythonコード付きで詳細説明をしていますので、是非参考にしてみて下さい。
その他「正則化(Regularization)」という言葉もありますが、これは過学習(学習し過ぎて汎用的に使えなくなる(汎化性能が低下するという))を防ぐために式に情報を追加することです。
標準化、正規化、正則化…この3つの言葉は明確に区別できるようにしておきましょう!
特徴量エンジニアリング:多変量データの取扱い
特徴量(変数)が少ない問題(\(x, y\)で示されるような2変数問題等)はわざわざ機械学習のアルゴリズムを使う必要は無いと考えられるため、一般に機械学習が必要な場面は多変量の場合になるはずです。
機械学習を実際に行う前には標準化や正規化の他にも、特徴量エンジニアリングがあります。
特徴量エンジニアリングとは、これから予測しようというモデルを構築するのに必要な特徴量を選択したり、データの形を変換することです。
特徴量エンジニアリングはおそらくデータの標準化や正規化と並び最も重要でかつ難しいと思われ、エンジニアの腕に大きく左右される領域であると考えられます。
例えば、国籍や性別といったカテゴリカル変数はそのままでは数値として扱えないため、one-hot-encodingと呼ばれる方法でデータを行列に変換する必要があります。
他には、特徴量が多変量の場合に多重共線性(マルチコ)があると予測精度が著しく低下してしまうといったこともあります。
これらの注意点は多変量解析の基礎である重回帰分析と同じです。
当ブログではこの辺りの詳細を「Python機械学習!scikit-learnによる重回帰分析」で説明していますので、こちらも参考にして頂ければと思います。
予測精度と汎化性能に関するテクニック
過学習を防ぐ工夫
教師あり学習を行う時、正解データ全てに対して予測結果が合っていれば良いということは一概に言えません。
あまりに学習するデータ全てにフィッティングさせ過ぎてしまうと、その名の通り過学習(オーバーフィッティング)が起こってしまい、未知のデータに対する汎化性能が落ちてしまいます。
機械学習のテクニックの1つに、データ全体を学習に使うトレーニングデータと検証に使うテストデータに分けるホールドアウト法というものがあります。
これはモデルの汎化性能を確認するために頻繁に使われる手法です。
また、正解データを複数に分割し、分割したブロックの組み合わせ数分ホールドアウト法を使ってモデルを検証・確認する交差検証(クロスバリデーション)というテクニックもあります。
クロスバリデーションは構築したモデルがどれだけ母集団に対処できるかどうかを検証するために用いられ、データをそれ以上集めるのが困難な状況等で活躍します。
具体的な機械学習法の紹介

ここからは具体的な機械学習の手法を紹介していきます。各手法にはそれぞれどんな特徴があり、どんな技術が使われているかを確認していきましょう。
線形回帰
線形回帰(Linear regression)とは、直線や平面、3次元を超えた場合は超平面で関数をデータにフィッティングさせる方法の総称です。
回帰対象のデータと関数(モデル)の誤差を定式化し、最小二乗法等の誤差最小化アルゴリズムを使って学習を進めます。
最小二乗法については「Pythonでカーブフィット!最小二乗法で直線近似する方法」の記事で式展開を紹介していますので、ご興味があれば参考にしてみて下さい。
単回帰分析
単回帰分析とは、単一の特徴量\(x\)で出力値\(y\)を予測する方法です。要は直線の式\(y=ax+b\)で近似するという最も基本的な回帰分析のことです。
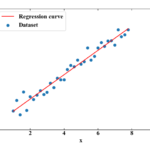
単回帰分析に関する詳細は「Python機械学習!scikit-learnによる単回帰分析」に記載しました。単回帰分析は手計算でも出来てしまうくらい簡単な内容ですが、Pythonの機械学習ライブラリscikit-learnの使い方を学ぶにはもってこいのコードも記載していますので、是非ご確認下さい。
重回帰分析
重回帰分析は特徴量が多変量になった回帰分析で、回帰式は\(y=\mathbf{w}^{\mathbf{T}}\mathbf{x}+w_{0}\)と偏回帰係数ベクトル\(\mathbf{w}\)と特徴量ベクトル\(\mathbf{x}\)、偏回帰定数\(w_{0}\)で表現します。
3次元の場合、下図のように平面でフィッティングするようになります。
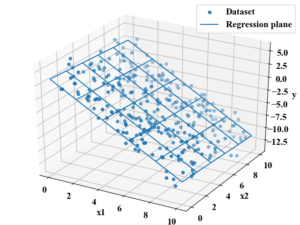
重回帰分析は多変量解析であるため、上述したように多重共線性の問題やカテゴリカル変数の取扱い方の他に、標準偏回帰係数、各特徴量の影響度分析等もキーワードになります。
詳しくは「Python機械学習!scikit-learnによる重回帰分析」という記事で説明していますので、是非ご確認下さい。
パーセプトロン
パーセプトロン(Perceptron)とは、1958年にフランク・ローゼンブラッドが論文を発表してから爆発的なニューラルネットワークのブームを巻き起こしたアルゴリズムです。
現在のニューラルネットワークの考え方はこのパーセプトロンを基本としているので、今後の学習のためにも是非理解したい所となります。
単純パーセプトロン
最も基本的なパーセプトロンを以下の図に示します。ここでは2入力ですが、複数の入力\(x\)に対して重み\(w\)をかけた後に足し合わせ、ステップ関数を使いある閾値を超えるかどうかで発火(1を出力)する構造を持ちます。
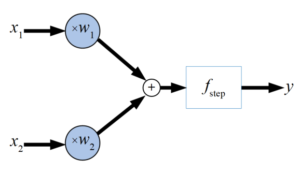
重みの数値を調整することで0と1になる条件を変えることができるため、分類問題に適用されるモデルとなります。
パーセプトロンを使うことで論理回路のような単純な分類問題を解くことができます。
当WATLABブログでは、パーセプトロンを使って以下の論理ゲートを実装した記事を公開していますので、こちらも是非ご覧頂けたらと思います。
・「PythonでパーセプトロンのANDゲートを実装する!」
・「PythonでパーセプトロンのORゲートを実装する!」
しかし、記事中でも紹介していますが、この単一のパーセプトロン、つまり単純パーセプトロンは線形分離可能な問題以外には適用できません。この問題を解決するためには次に紹介する多層パーセプトロンを使う必要があります。
多層パーセプトロン
多層パーセプトロン(MLP:Multi-Layer Perceptron)とは、先ほど紹介した単一のパーセプトロンを複数繋げたものです。
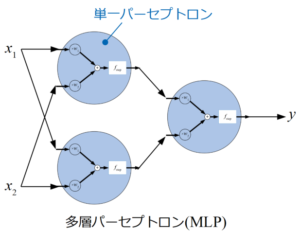
パーセプトロンを多層に繋げることで識別器としての表現力が増えるので、線形分離可能な問題以外にも適用することが可能になります。
多層パーセプトロンの詳細は「Pythonで多層パーセプトロンのXORゲートを実装する!」にて、なぜ多層にすることで複雑な問題を解けるようになるかも含めて解説していますので、こちらも参考にしてみて下さい。
サポートベクターマシン
サポートベクターマシン(SVM:Support Vector Machine)とは、教師あり学習のアルゴリズムの1つで、サポートベクトルとマージンという考え方を使って2クラス分類を行うことを基本的な目的としています。
SVMはマージンの最大化というコンセプトのもと非常に汎化性能の高い決定境界を引くことが可能です。
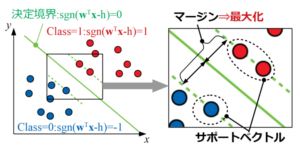
さらに、SVMはカーネル法という写像の考え方を使ってデータを高次元空間へマッピング(下図はイメージ)することで非線形分類も可能になります。
そしてカーネルトリックという手法で膨大な計算をしなくてよくなるというメリットも持ち、現在でも人気のあるアルゴリズムの1つです。
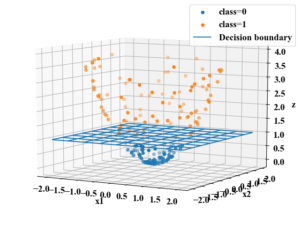
これらのキーワードの詳細は「Python機械学習初心者用!サポートベクターマシンの概要と実装」で紹介していますので、SVMの概要が不明な方は是非ご覧下さい。
また、SVMは回帰問題にも適用可能で、カーネル法やカーネルトリックのアルゴリズムを使って以下のような複雑な非線形関数もフィッティングすることが可能です。
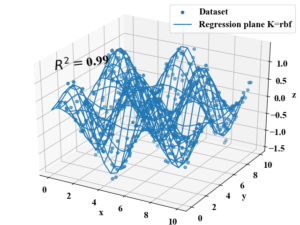
分類問題に適用するSVMをSVC(C=Classification)、回帰問題に適用するSVMをSVR(R=Regression)として呼び分けます。
SVRについては「Pythonサポートベクターマシンで回帰分析!SVRの概要と実装」に先ほどの非線形関数のフィッティングを含む詳細説明をしていますので、是非こちらも読んでみて下さい。
決定木分析
決定木(Decision tree)とは、不純度が最も減少するように条件分岐を作りデータを振り分ける教師あり機械学習手法です。
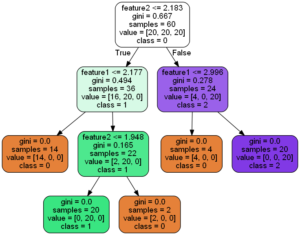
不純度とは、クラス分類をする時に、一方のクラスにどれだけ他のクラスのデータが混ざっているかの度合いを示す指標で、ジニ係数やエントロピーといった様々な指標が存在します。
決定木分析は条件分岐をして分類や回帰を行うため、複雑な問題にも容易に適用でき、かつ人間が解釈しやすいアウトプットを得ることができます。
以下の図は決定木分析でクラス分類を行った結果の例ですが、条件分岐の数を増やせば100%の正答率を得ることが可能です。
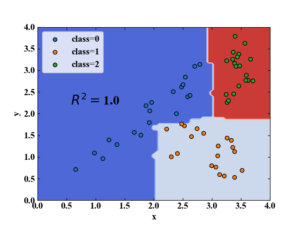
しかしながら、この性能に頼り切ってしまうと過学習に陥りやすく、木の深さや最小リーフ数等のハイパーパラメータを調整しなければ中々実問題で高い精度を得ることは困難と言われています。
決定木分析の詳細も「Python/sklearnで決定木分析!分類木の考え方とコード」で記事を公開していますので、必要に応じてご確認下さい。
ランダムフォレスト
ランダムフォレスト(Random Forest)とは、決定木を複数作成し、分類問題であれば多数決、回帰問題であれば平均をとって予測を行う手法です。
この多数決というアルゴリズムを導入することで、決定木が持つ過学習しやすいという欠点を緩和することに貢献しています(以下はイメージ図)。
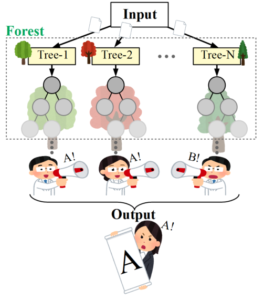
ランダムフォレストはアンサンブル学習の代表的な手法であるバギングを用いてランダムに複数の特徴量を選び、決定木の分岐ノードの条件式に使用する特徴を持ちます。
ランダムフォレスト関連の用語については「Python機械学習!ランダムフォレストの概要とsklearnコード」で概要説明とコード紹介をしていますので、詳細はこちらの記事をご確認頂ければと思います。
ロジスティック回帰
ロジスティック回帰(Logistic Regression)とは、線形回帰分析を分類問題に応用したアルゴリズムです。
ロジスティック回帰は病気の発生予測や商品の購買予測等、確率を検討する場合によく使われます。
ロジスティック回帰は、先に紹介した重回帰分析で使用した回帰式を基本としていますが、その式をさらにシグモイド関数の\(x\)に代入したものが回帰式として使われます。
シグモイド関数を利用することで事象の確率を扱えるようになります(以下はイメージ)。
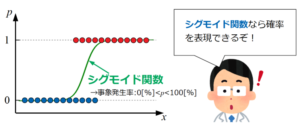
ロジスティック回帰のキーワードには、出力を0から1の値に正規化し、確率としての解釈を与える変換としてロジット変換、式中に出てくるオッズや対数オッズというワードがあります。
これらは「Python/sklearn機械学習!ロジスティック回帰で分類する」で式展開も含めた解説を行っているため、各ワードの関係が曖昧な方は参考になると思います。
k近傍法(kNN法)
k近傍法(kNN法:k-Nearest Neighbor Algorithm)とは、教師あり学習の一種で、最も近いk個のサンプルを使ってテストデータのクラスを予測する分類手法です(以下はイメージ)。
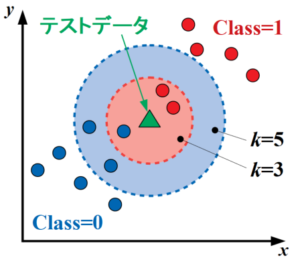
分類の場合は多数決、回帰の場合は平均を用いる点はランダムフォレストのやり方と似ています。
そしてこのkNN法は各種機械学習の中でも非常に簡単なアルゴリズムになっており、結果の理解が容易です。
しかし、テストデータから予測をするためには毎回全数のサンプルを計算しなければならない等、予測時にも計算コストがかかる欠点や、距離計算を行うので多次元データの場合に次元の呪いにはまりやすいといった欠点もあり、あまり実問題には使用されないといった実情もあります。
kNN法は「Python/sklearnのk近傍法!kNNで多クラス分類する」という記事でその他、アルゴリズムを改善したkNN法やハイパーパラメータ、Pythonコードを紹介していますので、こちらも是非ご覧ください。
クラスタリング
k-means法
k-means法とは、クラスタリングを行うアルゴリズムの1つで教師なし学習法の中の一手法でもあります。
これまで紹介してきた様々な機械学習アルゴリズムは全て教師あり学習でした。
kという名前が付いていますが、kNN法がテストデータ近傍のデータ数であるのに対し、k-means法のkはクラスタ数を意味します。
予めクラスタ数を設定し、ランダムなクラスタ中心をデータ群の中に置き、それらの点と最も近いデータを暫定クラスに設定、その後はデータの重心にクラスタ中心を移動して再度暫定クラスを…と繰り返していって丁度良いクラスタリングをするアルゴリズムです。
k-means法に関しては言葉で説明するよりも動画を見た方が一目瞭然ですので、以下に今回作成したYoutube動画を置いておきます。
この動画の詳細説明やk-means法の概要は「Python/k-means法で教師なし学習!クラスタリング概要」を参照下さい。この記事にはscikit-learn以外にもnumpyでk-means法のコードを自作したものを置いているので、もしかしたらアルゴリズム理解の参考になるかも知れません。
まとめ
本記事はG検定対策として、JDLAのシラバスに記載の「機械学習の具体的手法」と冒頭で紹介した参考書の問題から、Webやその他参考書で調査した内容をまとめた記事です。参考書「徹底攻略 ディープラーニングG検定ジェネラリスト問題集」を解きつつ本記事を参照頂ければ、より一層の理解が得られると思います。
結果としてG検定を目指している人以外にも、「機械学習って何?どんなことをやっているの?」という疑問にも答えられるような内容になったのではないかと思います。
本記事では機械学習を学習別分類として教師あり、教師なし、強化学習と整理し、具体的手法として様々なアルゴリズムを紹介しました。
もちろん、ここに記載の内容は機械学習の全てを語っているわけではなく氷山の一角ですが、これから機械学習を勉強する人のきっかけになってくれると良いと思います。
今回はG検定の学習ノートといえども、Pythonコードを扱った実践的な記事を多数紹介しました。
もしまだPythonを始めたことがなく、これからPythonプログラミングもやっていこうという方がいらっしゃいましたら、是非「Python入門!初心者がインストールから学習開始するまでの3ステップ」から独学可能なプログラマを目指していって頂けたらと思います。
G検定の合格率はそれほど低くないみたいだけど、実際にPythonプログラミングを動かしながら学んだ方が理解が深まって暗記勉強にならないと思います!是非今回紹介した記事をきっかけにプログラムコードを動かしてみて下さい!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント