
機械学習を使って学習や予測を行う際は、データの前処理は欠かすことのできないプロセスです。ここではデータの標準化と正規化の概要と必要性、Pythonとscikit-learnによるコーディング例を紹介します。
こんにちは。wat(@watlablog)です。
機械学習に使うデータは何でも良いわけではありません!ここではPython/scikit-learnによるデータの標準化と正規化を紹介します!
入力データの標準化と正規化の概要
標準化とは?
標準化(Standardization)とは、「平均を0に、標準偏差を1にするスケーリング」です。
世間では様々な意味合いで「標準化」という言葉が使われていますが、数学的な定義はこちらになります。
データセット\(x(i)\)を標準化したデータセット\(x_{std}(i)\)に変換する方法は、平均\(\bar{x}\)と標準偏差\(\sigma_{x}\)を用いて式(1)で行います。
\[x_{std}(i)=\frac{x(i)-\bar{x}}{\sigma_{x} } (1)\]
正規化とは?
正規化(Normalization)とは、「データを一定の規則に従って加工し、扱いやすくすること」です。
正規化はデータの種類によって様々な方法がありますが、特に機械学習の分野で使われる正規化には、データの値をある範囲内に収めるスケーリングが頻繁に使われます。
数あるスケーリングの中でも、データの最小値\(x_{min}\)と最大値\(x_{max}\)を使って0から1の値に変換する手法をMin-Maxスケーリングと呼びます。
Min-Maxスケーリングで正規化した値\(x_{norm}(i)\)を得るには式(2)を使います。
\[x_{norm}(i)=\frac{x(i)-x_{min}}{x_{max}-x_{min}} (2)\]
この方法は簡便であるため理解がしやすいですが、外れ値の影響を受けやすいという欠点を忘れてはいけません。
機械学習ではデータスケールが揃っていないと精度が落ちる
データの前処理はなぜ必要か?
機械学習ではトレーニングに使用するデータの質がその後の分類や予測問題の精度を決めます。
例えば人間の身長や体重の統計データをトレーニングに使う場合、あるデータはcmやg、またあるデータはmやkgを用いていたとします。
この時、データの単位を揃えないで計算をしてしまうことは誰が考えてもダメであることは明白ですが、身長や体重等異なる単位系のデータを扱う場合は「尺度」を揃えるということをしないと各パラメータの影響度を評価することはできません。
尺度というのは長さを測る時に使う言葉でもありますが、広義には「物事を評価する基準」という意味も持ちます。
例えば子どもと大人を分類する機械学習をする場合に身長をm、体重をkgで表していたとすると、身長よりも体重の方が数値自体の大きさは大きくなります。
コンピュータは僕達のような常識を持っていないので、同じ尺度にするためにスケーリングを行って評価した方がアルゴリズムがうまく働きます。
学習の効果を最大限に引き出すためにデータの前処理を検討しましょう。
機械にやさしいデータを前処理で作ってあげましょう!
scikit-learnによる標準化と正規化のコード
標準化のサンプルコード
早速Pythonのscikit-learnを使ったコードを書いていきます。まずは全コードを以下に示します。
標準化に必要なライブラリは「from sklearn.preprocessing import StandardScaler」としてimportします。
用意するデータは「Python機械学習!scikit-learnによる単回帰分析」で用意したノイズを含んだ自作のデータセットです。
標準化をしている部分は「sc = StandardScaler()」で標準化のモジュールを呼び出し、「std = sc.fit_transform(data)」でデータセットの統計的な指標を計算(fit)し、その値(平均や標準偏差)を使ってデータセットを変換(transform)しているというたった2行の部分になります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
from sklearn.preprocessing import StandardScaler import numpy as np from matplotlib import pyplot as plt # データを用意する a = 1.0 # 直線の傾き b = 0.5 # y切片 x = np.arange(1.0, 8.0, 0.2) # 横軸を作成 noise = np.random.normal(loc=0, scale=0.5, size=len(x)) # ガウシアンノイズを生成 y = a * x + b + noise # サンプル波形 data = np.c_[x, y] # x,yを結合 # 用意したデータ各列の平均と標準偏差を確認 print(np.mean(data[:, 0]), np.mean(data[:, 1])) print(np.std(data), np.std(data[:, 1])) # 標準化を行う sc = StandardScaler() std = sc.fit_transform(data) # 標準化したデータ各列の平均と標準偏差を確認 print(np.mean(std[:, 0]), np.mean(std[:, 1])) print(np.std(std[:, 0]), np.std(std[:, 1])) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットする。 ax1.scatter(x, y, label='Dataset') ax1.scatter(std[:, 0], std[:, 1], label='Standardized') plt.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
途中、print()文で元のデータの平均と標準偏差、標準化後のデータの平均と標準偏差を表示させていますが、本コードを実行すると以下のような結果を得ます。
想定通り、変換後の平均がほぼ0(完全に0になっていないのは数値誤差と考えられる)、標準偏差が1になっていることが確認できました。
|
1 2 3 4 5 |
4.4 4.733685076706672 # 元データの平均[x, y] 2.085130962042093 2.1353850689102423 # 元データの標準偏差[x, y] -5.51939446527935e-16 -3.743037625879099e-16 # 標準化後データの平均[x, y] 1.0 1.0000000000000002 # 標準化後データの標準偏差[x, y] |
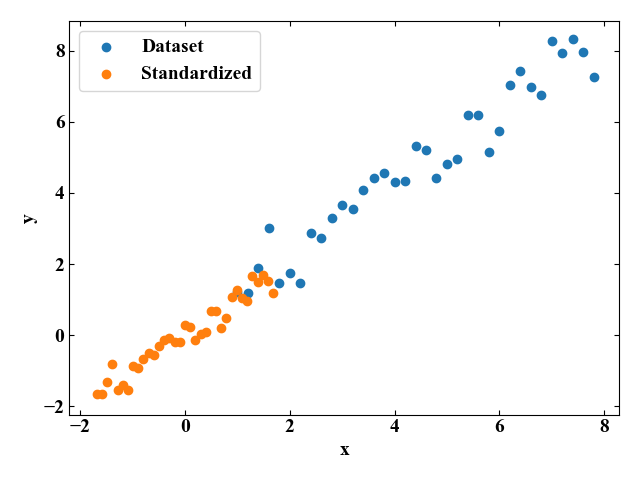
元のデータセット(Dataset)と標準化後のデータセット(Standardized)をmatplotlibを使ってグラフにプロットすると以下の図が得られます。
変換後は0付近に分布していますね。
正規化のサンプルコード
続いてMinMaxスケーリングによる正規化コードを書いていきます。
今回は「from sklearn.preprocessing import MinMaxScaler」とMinMaxスケーリングのライブラリをimportしています。
標準化の時と書き方は同じで「mms = MinMaxScaler()」でMinMaxスケーリングのモジュールを呼び出し、「norm = mms.fit_transform(data)」で実際にfitとtransformを同時に実行します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
from sklearn.preprocessing import MinMaxScaler import numpy as np from matplotlib import pyplot as plt # データを用意する a = 1.0 # 直線の傾き b = 0.5 # y切片 x = np.arange(1.0, 8.0, 0.2) # 横軸を作成 noise = np.random.normal(loc=0, scale=0.5, size=len(x)) # ガウシアンノイズを生成 y = a * x + b + noise # サンプル波形 data = np.c_[x, y] # x,yを結合 # 用意したデータ各列の最大値と最小値を確認 print(np.max(data[:, 0]), np.max(data[:, 1])) print(np.min(data[:, 0]), np.min(data[:, 1])) # 正規化を行う mms = MinMaxScaler() norm = mms.fit_transform(data) # 正規化したデータ各列の最大値と最小値を確認 print(np.max(norm[:, 0]), np.max(norm[:, 1])) print(np.min(norm[:, 0]), np.min(norm[:, 1])) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットする。 ax1.scatter(x, y, label='Dataset') ax1.scatter(norm[:, 0], norm[:, 1], label='Normalized') plt.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
上記コードを実行すると以下の結果を得ます。コンソールに表示された数値から、正規化後は最大値が1, 最小値が0のデータになっていることが確認できました。
|
1 2 3 4 5 |
7.799999999999999 8.786895227121015 # 元データの最大値[x, y] 1.0 1.274594283212542 # 元データの最小値[x, y] 1.0 1.0 # 正規化後データの最大値[x, y] 0.0 0.0 # 正規化後データの最小値[x, y] |
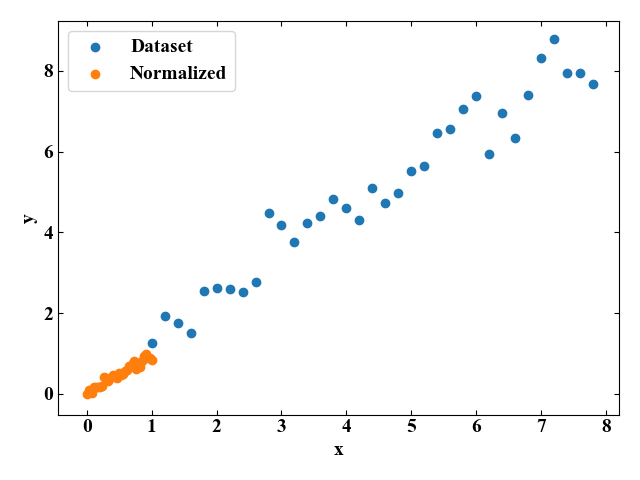
グラフに元データセットとMinMaxスケーリングによる正規化後データセットをプロットすると以下の図を得ます。
まとめ
本記事では機械学習プログラムの入力データには前処理が重要であることを説明し、標準化と正規化の例を紹介しました。
また、機械学習でよく使われるPythonのscikit-learnというライブラリを使った標準化と正規化のプログラミング例を紹介し、グラフプロットとprint文による結果の確認までを行いました。
実際には勾配降下法を使う場合、画像データを使う場合、活性化関数の種類…等によってこれらの標準化と正規化を使い分けるとのことですが、学習を進めて行くなかでそれらの問題に直面した時に再度記事にして紹介したいと思います。
「データの前処理」は地味ながら最も大事なことで、意外とかなりの時間を使って作業することと推定します!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント