
機械学習のアルゴリズムの中でも優秀な識別器であるサポートベクターマシン(SVM)はPythonのscikit-learnで簡単に実装することが出来ます。ここではサポートベクターマシンを実際に使うために必要な知識の概要とPythonによるサンプルコードを紹介します。
こんにちは。wat(@watlablog)です。サポートベクターマシン(SVM)は高度な理論に基づき構成されていますが、実装自体は簡単です!ここではSVMを使用するために必要な最低限の知識と実装コードの紹介を行います!
サポートベクターマシンの概要
サポートベクターマシン(SVM)とは?
サポートベクターマシン(SVM:Support Vector Machine)とは、教師あり学習のアルゴリズムの1つで、後述するサポートベクトルとマージンという考え方を使って2クラス分類を行うことを基本的な目的としています。
クラス(Class)とは、例えばペンや消しゴムは文房具というクラス、車や自転車は乗り物というクラス、というように、分類の種類を意味します。
2クラス分類問題は以下の図に示すように、複数の特徴量(ここでは\(x\)と\(y\)の2つ)で説明された2種類のクラス(Class=0, Class=1)を明確に分ける線を引くことと同じです。このクラスを分ける境界線のことを決定境界と呼びます。
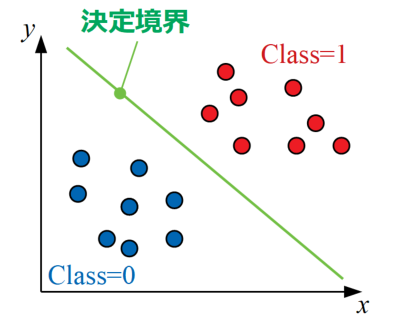
SVMは元々2クラス分類を基本としていましたが、現在では多クラスへの拡張や回帰問題への適用等にも応用されてきています。
奥が深いSVMですが、ここでは最も基本的な2クラス分類の計算について説明していきます!
ちなみに、サポートベクターマシンを使った回帰分析(SVR)は「Pythonサポートベクターマシンで回帰分析!SVRの概要と実装」で紹介していますので、ご興味がございましたら是非見てみて下さい!
パーセプトロンとの違い
SVMは分類問題に使う計算アルゴリズムということですが、当WATLABブログでは過去「Pythonで多層パーセプトロンのXORゲートを実装する!」という記事で単純パーセプトロンや多層パーセプトロンを紹介してきました。
どちらも分類に使用するアルゴリズムだけど、何が決定的に違うのだろうか?
パーセプトロンを使った学習では、重み\(w\)と閾値\(\theta\)というパラメータを調整して、うまいこと目的の分類ができる組み合わせを見つける作業が必要でした。
それは人が調整しても、誤差関数を導入して機械的にやろうとしても変わりはなく、最終的に決定された境界線が以下の図のAやBであっても良しとするアルゴリズムです。
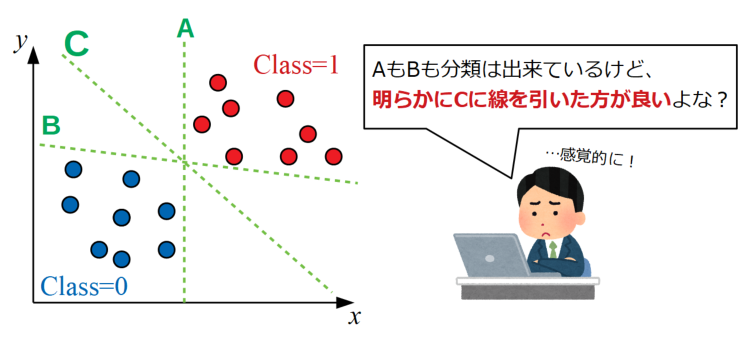
しかし、僕達人間は感覚的にCのあたりに線を引いた方が良いのではないか?と感じると思います。
機械学習の目的は未知のデータが入力された時に、そのデータが何であるかを予測する所にあるので、できるだけデータ群から離れた位置に線を引いた方が、新規データが下図のように少し外れた点に来ても安心です。上記感覚はこの目的から来るものと考えられます。
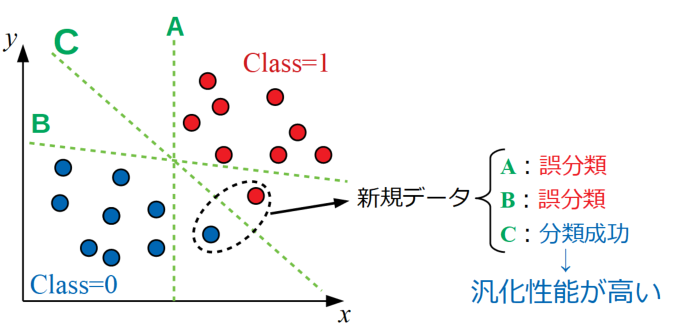
決定境界は学習したデータ群から外れたサンプルに対する余裕があるほど汎用性が高く、この性能のことを汎化性能と呼びます。
サポートベクターマシンはパーセプトロンのように逐次計算によって重みを調整するのでは無く、決定境界とデータの距離(つまりマージン)を最大にするコンセプトのもと設計されており、汎化性能の向上を狙った分類器であると言う事が出来ます。
サポートベクターマシンを理解するのに必要な要素
分類問題を式で見てみよう
データをクラスに分類する問題の基本はパーセプトロンの記事で書いた内容と同様の考え方をします。サポートベクターマシンを理解するために、まずは基本であるパーセプトロンからおさらいしましょう。
「PythonでパーセプトロンのANDゲートを実装する!」で紹介したように、単純パーセプトロンは重み\(w\)と入力\(x\), 閾値\(\theta\)を用いて式(1)で記述することが可能です(ここでは2入力の場合)。
\[
y = \begin{cases}
0 & (w_{1}x_{1}+w_{2}x_{2}\leq \theta) \\
1 & (w_{1}x_{1}+w_{2}x_{2}> \theta)
\end{cases} (1)
\]
式(1)は2入力の場合ですが、複数入力に対応させた場合は重みベクトル\(\mathbf{w}\)と入力ベクトル\(\mathbf{x}\)を導入することで、式(1)の括弧内左辺は式(2)とベクトルの内積の形で書くことが出来ます。
\[
w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n}=\mathbf{w}^{\mathbf{T}}\mathbf{x} (2)
\]
Tは転置を意味します!\(\mathbf{w}\)を転置しないと展開した時の結果が変わってしまいます。
さらに、閾値\(h\)(他の論文(下に記載の参考文献)やWebサイトには閾値は\(h\)と書いてあったので\(h\)にしました。)を左辺に持ってきて、線形識別関数\(\mathrm{sgn}\)を使うと式(3)とシンプルに記述することができます。
\[
y=\mathrm{sgn}(\mathbf{w}^{\mathbf{T}}\mathbf{x}-h) (3)
\]
この線形識別関数\(\mathrm{sgn}\)は0を超えた数は1、0未満の数は-1を返す関数であり、式(3)は重みベクトルと入力ベクトルの内積スカラー値\(\mathbf{w}^{\mathbf{T}}\mathbf{x}\)が閾値\(h\)を超えたら1、超えなかったら-1を返す分類問題を表現していることになります。
機械学習関係ではこの形の式がよく出てくるので、早めに慣れておきたいですね。
問題が線形分離可能であれば、この式(3)のパラメータ(\(\mathbf{w}\)と\(h\))を変えることで完全な決定境界を求めることが可能です。そしてここまではSVMであってもパーセプトロンであっても考え方は同じです。
サポートベクターマシンの場合はここにサポートベクトルとマージンという考え方を導入している所が特徴です。
サポートベクトルとマージンの考え方
ここでまずはサポートベクトルとマージンという言葉を説明します。図示が容易なのでサポートベクトルとマージンを以下の2Dプロットの場合で図に示します。
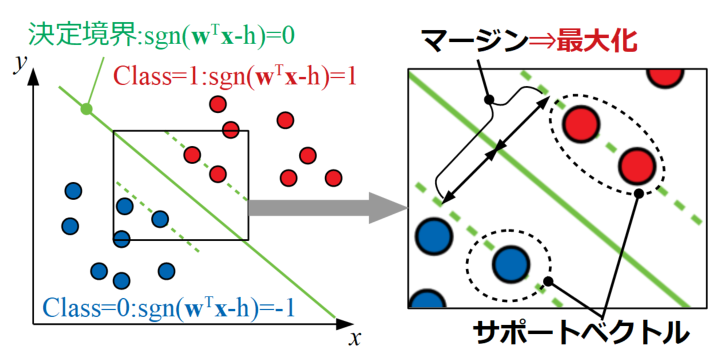
図中の青●はClass=0のデータですが、式を使った表現としては\(\mathrm{sgn}(\mathbf{w}^{\mathbf{T}}\mathbf{x}-h)\)が-1になる領域となります。同じくClass=1の赤●部分は\(\mathrm{sgn}(\mathbf{w}^{\mathbf{T}}\mathbf{x}-h)\)が1になる領域となり、真ん中の決定境界は\(\mathrm{sgn}(\mathbf{w}^{\mathbf{T}}\mathbf{x}-h)\)が0となる線です。
ここで、それぞれの領域の決定境界から最も近い点がサポートベクトルと呼ばれるもので、このサポートベクトル(最も近い訓練データ)と決定境界の距離をマージンと呼びます。
このマージンを最大化する問題を解くことで、それぞれの領域から最も遠い所に決定境界を引くことができ、それが汎化性能の向上に寄与するということになります。
マージンの表現:ヘッセの公式からの拡張
マージンを最大化するためには、まず直線(2次元の場合は平面、多次元の場合は超平面)\(\mathbf{w}^{\mathbf{T}}\mathbf{x}-h=0\)とサポートベクトルとの距離を求める必要があります。
直線と点の距離を求めるためにはヘッセの公式が有名です。この公式を今回の超平面の場合に当てはめると式(4)と書くことが可能です(公式自体の証明は外部サイト様がわかりやすくまとめていましたので、ご参考)。
\[
d=\frac{\left | w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n}-h \right |}{\sqrt{w_{1}^{2}+w_{2}^{2}+\cdots +w_{n}^{2}}} (4)
\]
式(4)はヘッセの公式の形に近づけましたが、ベクトル形式に変換し、さらに超平面の係数ベクトルをノルム(長さ)\(\left || \mathbf{w} |\right |\)を使って書くと式(5)と表現することが出来ます。
\[
d=\frac{\left | \mathbf{w}^{\mathbf{T}}\mathbf{x}-h \right |}{\left || \mathbf{w} |\right |} (5)
\]
式(5)の方がシンプルですね!
ここまで定義できたら、後は実際の訓練データのどこが超平面と近いのか、その距離を最大化するために最小化問題に変換して解くという作業になりますが、ここからはページ下に示す参考文献に丸投げしてしまいます(長いので…)。
1点、特に重要な点として、参考文献の式(23)で最適化する問題は特徴量ベクトルの内積計算ができれば良いという所が挙げられます。これは後述するカーネルトリックのキーポイントとなっており、SVMを有名にした技術でもあります。
カーネル関数により線形分離不可能な問題へ対応
ここまではデータが線形分離可能な問題に対する説明のみでしたが、SVMは一見すると線形分離不可能な問題でも線形分離をすることができる点が世間で使われている理由でもあります。
写像による変換で線形分離可能にする考え方
例えば以下の図に示す2つのクラスは特徴量\(x_{1}\)と\(x_{2}\)によって表現されています。僕達人間が見れば円の中心付近にclass=0、外側にclass=1があるという分類をすることができますが、どうやっても直線で分けることはできません。
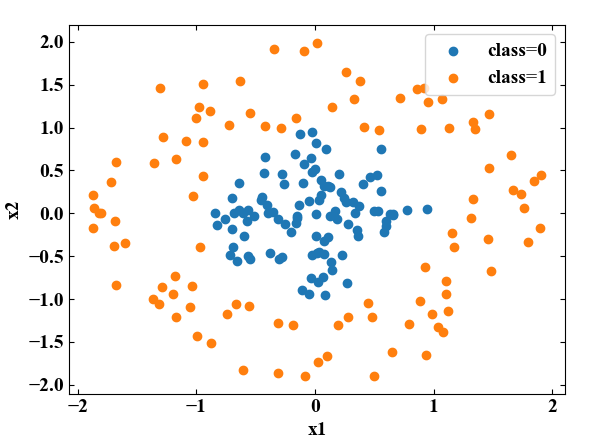
しかし、以下の図のように特徴量\(z\)を新たに追加する変換(特徴量ベクトル\(\mathbf{x}\) を写像によって\(\mathbf{\phi}\) へ変換)を施すことで平面で分離できるため、これは線形分離可能な問題に変換したことになります。

写像と聞くと難しく構えてしまいそうですが、うまく線形分離可能となるように特徴量を増やしてあげることができるということですね。
カーネル関数とは?カーネルトリックによる計算コスト低減
写像の考え方を使えば、一見すると線形分離不可能な問題へも対応できるようになることがわかりました。
しかし、前述したように、マージンの最大化を行うためには特徴量ベクトルの内積計算を行う必要があります。
写像によって新しい特徴量を増やすと、特徴量の数が大きい場合は非常に膨大な演算を必要としてしまいますが、そこで登場するのがカーネル関数です。
カーネル関数とは、非線形空間へ写像した後の特徴量ベクトルの内積を、元の特徴量ベクトルのみを使って計算することができる関数(式(6)の\(K\))のことです。
\[
K(\mathbf{x_{1}}, \mathbf{x_{2}})=\mathbf{\phi_{1}}^{\mathbf{T}}\mathbf{\phi_{2}} (6)
\]
元の特徴量ベクトルだけで内積を計算することができるので、特徴量の次元が大きいケースでも現実的な計算量で済むことが最大のメリットです。
非線形カーネル関数には代表的な物に多項式カーネル、RBFカーネル(ガウスカーネル)、シグモイドカーネル等がありますが、詳細は実際に使ってみて別記事でまとめようと思います。
ハードマージンとソフトマージン
現実の問題はノイズだらけ
SVMを使うことで、線形でも非線形でも分類問題を扱えることができるとわかりました。
しかしながら、現実の問題(リアルワールドプロブレム)は全てのケースで綺麗に分類できるとは限りません。
例えば、現実のデータには必ず誤差を含みます。外れ値として実際にはありえない値をとることもあるでしょう。データの前処理でこれらのノイズを適切に処理することが望ましいですが、完全にノイズの影響を排除することはできません。
そのため、誤分類を許容する考えを導入する必要があります。
誤分類を許容しない、つまり完全に分類させるように決定したマージンをハードマージン、誤分類を許容するように決定したマージンをソフトマージンと呼びます。
現実の問題はほとんどがソフトマージン問題と言えそうですね。
以下に誤分類を許容しない場合と許容する場合の分類結果を例として示します。
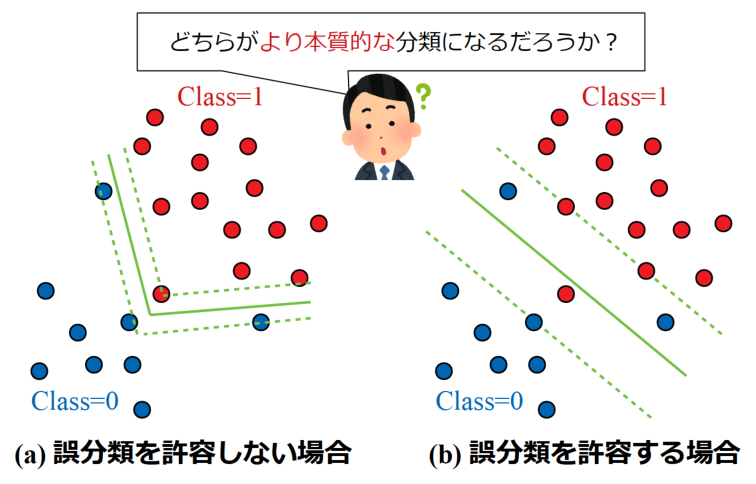
SVMはカーネル関数の導入により非線形問題も容易に扱えますが、(a)のように訓練データに特化したスペシャルな線を使った方が良いのか、(b)のように誤分類を許容してもマージンを大きくとった方が良いのかは、結局はデータによります。
しかし仮に(a)の分類の仕方がノイズの影響を受けていた場合、新しいテストデータに対する汎化性能は著しく低くなってしまいます。
訓練データに特化して学習しすぎてしまった結果を過学習と呼びますが、どのような決定境界の仕方が最も良いかの判断は、結局はエンジニアの腕の見せ所であると言えそうです。
本質を判断するというのは、まだまだエンジニアの役割として大きい要素ですね!
以下に簡単ですが、誤分類を許容するソフトマージンの考え方を少し説明します。
スラック変数\(\xi _{i}\)導入と正則化パラメータ\(C\)で誤分類を許容する
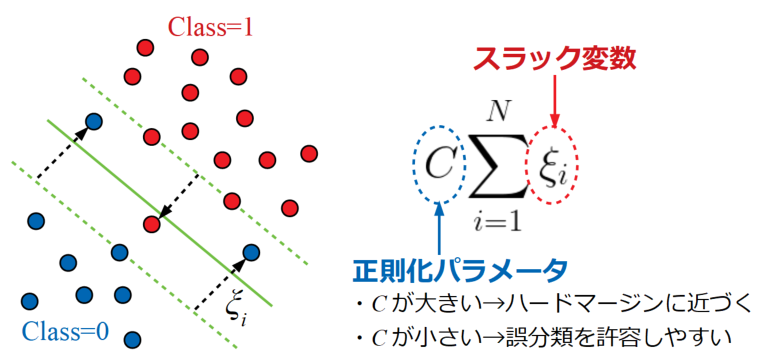
誤分類を許容するためにスラック変数\(\xi _{i}\)と呼ばれる変数を導入します。
スラック変数\(\xi _{i}\)とは、データ点が分類の反対側にどれだけ入り込んだかという距離を意味します。
下図にソフトマージン問題の例を示します。ここでは青い点●が2つ、赤い点●が1つ決定境界の反対側に入り込んでいます。
全てのスラック変数の和\(\sum_{i=1}^{N}\xi _{i}\)に対し、正則化パラメータ\(C\)をかけ、この正則化パラメータ\(C\)の値を調整することで「どれくらい誤分類を許容するか」を制御します。
この正則化パラメータ\(C\)はSVMモデルを構築する際にエンジニアが事前に調整すべきパラメータで、ハイパーパラメータと呼ばれます。
超平面はHyper planeって言うし、機械学習分野の用語はカッコいいですね。
Python/sklearnによるサポートベクターマシンの実装コード
前置きとして上記基礎知識を概要としてまとめましたが、SVMはPythonのscikit-learnを使えば簡単に実装することが可能です。
使うだけなら誰でもできてしまいますが、できるだけ何をやっているかを理解しようとすることは大事だと思います。
ここからはscikit-learnを使ったSVMの実装を紹介します。
全コード
まずは説明よりも前に、全コードと実行結果を載せます。
以下が全コードで、訓練データの生成や正解ラベリング、SVMによる学習と結果の可視化プロットまでの一連の計算を書いています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
import numpy as np import pandas as pd from sklearn import svm from matplotlib import pyplot as plt # データを用意する------------------------------------------ # 線形分離可能なデータセットを生成する n = 20 # クラス毎のデータ数 df = pd.DataFrame() # データフレーム初期化 for i in range(2): # データ作成ループ x = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなx値を計算 y = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなy値を計算 label = pd.Series(np.full(n, i)) # ラベル(クラス)を作成 temp_df = pd.DataFrame(np.c_[x, y, label]) # クラス毎のデータフレームを作成 df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合 df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化 # クラス毎のデータフレームに分離(プロット用) class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 # ---------------------------------------------------------- # 学習させる値(訓練データ)とクラス(正解ラベル)に分離 data = df[[0, 1]] # 訓練データ data_class = pd.Series(df[2]) # 正解ラベル # サポートベクターマシンによる学習 clf = svm.SVC(C=1.0, kernel='linear') # 正則化パラメータ=1, 線形カーネルを使用 clf.fit(data, data_class) # フィッティング # 決定境界可視化用 grid_line = np.arange(-10, 10, 0.05) # グリッドデータのための配列を生成 X, Y = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測 Z = Z.reshape(X.shape) # 3Dプロットするためにshapeを再変換 # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' fig = plt.figure() ax1 = plt.subplot(111) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 2) ax1.set_ylim(0, 2) # データプロットする。 ax1.contourf(X, Y, Z, cmap='coolwarm') ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') plt.legend() # グラフを表示する。 plt.show() plt.close() |
実行結果
上記コードをそのままコピペして実行すると、以下のグラフがプロットされます。
これは、class=0とclass=1に予め分類した訓練データを学習しモデルを構築、構築したモデルをグリッド軸を使ってデータが取り得る範囲を網羅的に可視化したものです。
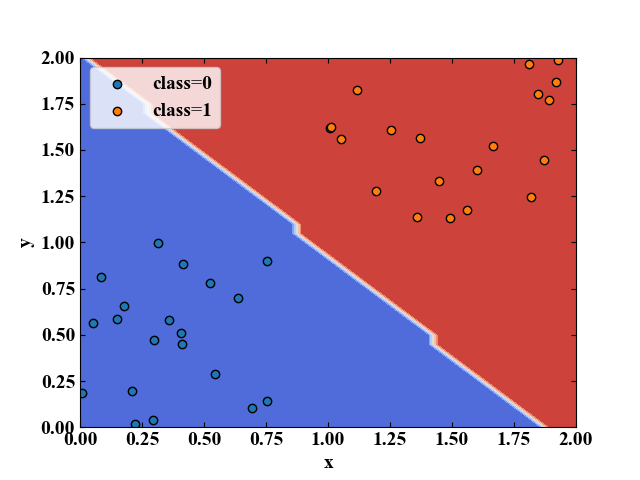
しっかり分類されていますね!
コード詳細説明
importするライブラリ
numpy, matplotlibはデータの操作やグラフ作成でいつも使うおなじみのライブラリですが、今回のサポートベクターマシンを実装するにあたり、pandasとsklearnが特に必要なライブラリとなります。
|
1 2 3 4 |
import numpy as np import pandas as pd from sklearn import svm from matplotlib import pyplot as plt |
pandasはデータの加工や生成が得意なライブラリで、機械学習用データ処理によく使われています。概要は過去に「Python/Pandasの基本操作!データフレーム行列の取扱い」で紹介していますので、是非参考にしてみて下さい。
sklearnはscikit-learnの略で、機械学習の関数が豊富にあるライブラリです。scikit-learnでできることの概要は「Python機械学習!scikit-learnインストールと例題」で紹介しているサンプルコードを実行するとよくわかると思いますので、こちらも併せて参考にして頂ければ幸いです。
サンプルデータ生成:データフォーマットの説明
今回はサンプルデータとしてランダムなデータ群を生成しています。以下の「# データを用意する」とコメントしている部分がデータ生成部になります。
実際の問題に機械学習を使う時、この部分は外部のcsvファイルや別途データセットをimportする部分です。その際はpandasのデータフレーム形式で読み込むことが多いと思われたため、データフォーマットをpandas形式にしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# データを用意する------------------------------------------ # 線形分離可能なデータセットを生成する n = 20 # クラス毎のデータ数 df = pd.DataFrame() # データフレーム初期化 for i in range(2): # データ作成ループ x = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなx値を計算 y = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなy値を計算 label = pd.Series(np.full(n, i)) # ラベル(クラス)を作成 temp_df = pd.DataFrame(np.c_[x, y, label]) # クラス毎のデータフレームを作成 df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合 df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化 # クラス毎のデータフレームに分離(プロット用) class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 # ---------------------------------------------------------- |
データは0列目に特徴量\(x\)、1列目に特徴量\(y\)、 2列目にクラス(class=0, class=1)が来るように配置しています。今回はfor文を使って書いていますが、最終的にprint(df)で以下の形式になっていればここで紹介しているSVMコードがそのまま使えます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
0 1 2 0 0.196455 0.598351 0.0 1 0.137064 0.813103 0.0 2 0.199091 0.210212 0.0 3 0.207436 0.471487 0.0 4 0.660173 0.218235 0.0 5 0.318533 0.338099 0.0 ... 35 1.433820 1.956859 1.0 36 1.648099 1.374384 1.0 37 1.518218 1.968999 1.0 38 1.566391 1.396689 1.0 39 1.764611 1.606198 1.0 |
訓練データと正解ラベルをセットしSVMを実行する
データが用意できたら、SVMの実行はものすごく簡単です。
まず用意したデータを訓練データと正解ラベルに分離し、.SVCでサポートベクターマシンを用意、.fitで計算をします。
|
1 2 3 4 5 6 7 |
# 学習させる値(訓練データ)とクラス(正解ラベル)に分離 data = df[[0, 1]] # 訓練データ data_class = pd.Series(df[2]) # 正解ラベル # サポートベクターマシンによる学習 clf = svm.SVC(C=1.0, kernel='linear') # 正則化パラメータ=1, 線形カーネルを使用 clf.fit(data, data_class) # フィッティング |
SVCはSupport Vector Classificationの略で分類問題で扱うサポートベクターマシンという意味です(本ページではやりませんが、サポートベクター回帰という回帰問題に使うSVMもあります)。
SVCについて詳しくは公式ページをご覧ください。
公式ページ:https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
ここでは概要で説明した正則化パラメータ\(C\)は1、カーネル関数\(K\)は線形カーネルという最も基本的な設定にしています。
デフォルトではlinearではなくrbf(RBFカーネル)ですが、何が何でも非線形カーネルを使っておけば良いというわけではないみたいです。線形で十分な分類は線形カーネルを使いましょう。
テストデータで予測結果を確認(グリッドで可視化)
.fitの後はテストデータを入力し、SVMで構築したモデルを使って実際の分類問題を解きます。
データは訓練データと同じように特徴量の種類毎に列で並べたフォーマットにしている必要があります。
今回のコードでは特徴量xとyの組み合わせをグリッドで与えて網羅的に分類結果を見るということをしています。そのため、.meshgridを使いグリッドデータをテストデータとしています。
|
1 2 3 4 5 |
# 決定境界可視化用 grid_line = np.arange(-10, 10, 0.05) # グリッドデータのための配列を生成 X, Y = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測 Z = Z.reshape(X.shape) # 3Dプロットするためにshapeを再変換 |
グリッドで生成した特徴量データセットを、.predictに渡せるデータ形式にするために、.ravel()を使っています。
以下に.ravel()で行っている変換例を示します。このように、.ravel()を使うことで多次元配列を1行にまとめることができます。
|
1 2 3 4 5 6 7 8 9 10 11 |
# print(X) [[-10. -9.95 -9.9 ... 9.85 9.9 9.95] [-10. -9.95 -9.9 ... 9.85 9.9 9.95] [-10. -9.95 -9.9 ... 9.85 9.9 9.95] ... [-10. -9.95 -9.9 ... 9.85 9.9 9.95] [-10. -9.95 -9.9 ... 9.85 9.9 9.95] [-10. -9.95 -9.9 ... 9.85 9.9 9.95]] # print(X.ravel()) [-10. -9.95 -9.9 ... 9.85 9.9 9.95] |
その後、「np.array([X.ravel(), Y.ravel()]).T」で訓練データと同じように列方向にデータが並ぶようにしています。
線形分類不可能なデータをRBFカーネルで分類してみる
では最後に線形分離不可能なデータセットを生成し、非線形カーネルであるRBFカーネルを設定してSVMをしてみましょう。
全コードは以下ですが、「# データを用意する」という部分と「kernel='rbf', gamma='scale'」という部分が異なるだけです。
RBFカーネルの場合は\(C\)以外にも\(\gamma\)がハイパーパラメータとなります(詳しくは別記事で)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
import numpy as np import pandas as pd from sklearn import svm from matplotlib import pyplot as plt # データを用意する------------------------------------------ # 線形分離不可能なデータセットを生成する n = 100 # クラス毎のデータ数 df = pd.DataFrame() # データフレーム初期化 theta = pd.Series(np.linspace(-np.pi, np.pi, n)) for i in range(2): # データ作成ループ x = pd.Series(np.cos(theta) * np.random.uniform(i, i + 1, n)) # ランダムなx値を計算 y = pd.Series(np.sin(theta) * np.random.uniform(i, i + 1, n)) # ランダムなy値を計算 label = pd.Series(np.full(n, i)) # ラベル(クラス)を作成 temp_df = pd.DataFrame(np.c_[x, y, label]) # クラス毎のデータフレームを作成 df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合 df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化 # クラス毎のデータフレームに分離 class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 # ---------------------------------------------------------- # 学習させる値(訓練データ)とクラス(正解ラベル)に分離 data = df[[0, 1]] # 訓練データ data_class = pd.Series(df[2]) # 正解ラベル # サポートベクターマシンによる学習 clf = svm.SVC(C=1.0, kernel='rbf', gamma='scale') # 正則化パラメータ=1, RBFカーネルを使用 clf.fit(data, data_class) # フィッティング # 決定境界可視化用 grid_line = np.arange(-10, 10, 0.05) # グリッドデータのための配列を生成 X, Y = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測 Z = Z.reshape(X.shape) # 3Dプロットするためにshapeを再変換 # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' fig = plt.figure() ax1 = plt.subplot(111) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(-3, 3) ax1.set_ylim(-3, 3) # データプロットする。 ax1.contourf(X, Y, Z, cmap='coolwarm') ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') plt.legend() # グラフを表示する。 plt.show() plt.close() |
このコードを実行すると以下の図を得ます。決定境界は見事円形にも対応できています。
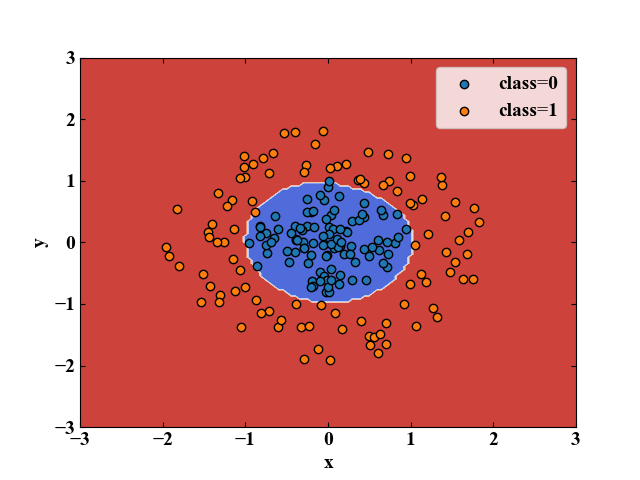
こんなに簡単なコードで複雑な分類を高速にできるとは!ちょっと感動しました!
まとめ
本記事では、教師あり学習のアルゴリズムの1つであるサポートベクターマシン(SVM)の概要を説明しました。
SVMはサポートベクトルを使ったマージン最大化というコンセプトを持ち、パーセプトロンと比べると汎化性能が高い識別器ということがわかりました。
また、非線形カーネル関数を使うことで一見線形分離不可能なデータセットも、高次元に写像することで分類可能になることもわかりました。
さらに、高次元の写像をしつつもベクトルの内積計算を元の特徴量だけで行うカーネルトリックを使うことで、複雑な問題でも計算量がそれほどかからないというメリットを理解しました。
最後に、実際にPythonのscikit-learnによるSVMコードを紹介し、線形、非線形の分類問題を解くことができることを体感しました。
サポートベクターマシンを使えばかなりの分類問題を解決することができそうですね!機械学習っぽくなってきて楽しくなってきました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!
参考文献
栗田 多喜男, サポートベクターマシン入門:
https://home.hiroshima-u.ac.jp/tkurita/lecture/svm.pdf

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント