機械学習のニューラルネットワークはパーセプトロンを基礎としています。パーセプトロンは線形分離可能な問題にしか適用できませんが、多層に連結することでその壁を超えることができます。ここではPythonを使って多層パーセプトロンのコーディングを習得します。
こんにちは。wat(@watlablog)です。
単一のパーセプトロンから発展し、ここでは多層パーセプトロンをコーディングしてみます!
単一パーセプトロンのおさらい
パーセプトロンは可変の線形識別器になる
パーセプトロンとは、以下の図に示すように\(n\)個の入力\(x_{n}\)を重み\(w_{n}\)をかけてから足し合わせ、ある閾値\(\theta\)を使ったステップ関数\(f_{step}\)を通して0か1の出力\(y\)を得るモデルです。
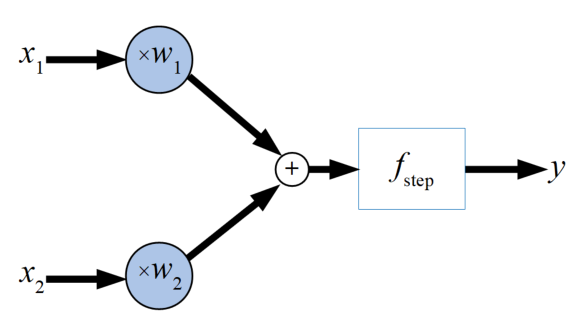
このモデルを絵ではなく式にすると以下の式(1)で書くことができます。
非常に簡単な式ではありますが、この式の重み\(w_{n}\)と閾値\(\theta\)を変えるだけで線形の識別器が作れてしまう優れものなのです。
\[
y = \begin{cases}
0 & (w_{1}x_{1}+w_{2}x_{2})\leq \theta \\
1 & (w_{1}x_{1}+w_{2}x_{2})> \theta
\end{cases} (1)
\]
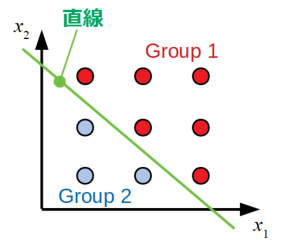
つまりパーセプトロンは、以下の図に示すように入力に対して赤丸や青丸のような2つのグループに分ける問題を出した時に直線で適切に分類することができるモデルということです。
AND/OR/NANDの論理ゲートを再現する(コード付き)
パーセプトロンには良く知られた代表的な例題として、論理演算(ブーリアン演算)があります。
多層パーセプトロンに行く前に単一パーセプトロンで構築された論理ゲート問題を解いてみましょう。
ANDゲート
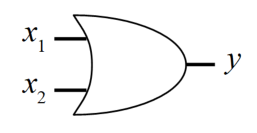
ANDゲートは以下の図で示される論理回路で、日本語で論理積を意味します。
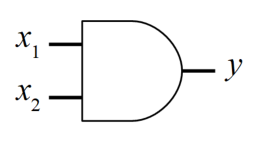
積を計算するため真理値表は下表になり、全ての入力が1にならないと1を返しません。
| \(x_{1}\) | \(x_{2}\) | \(y\) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
ここでいう1はTRUE(真)、0はFALSE(偽)と表現することもあります。
ANDゲートをパーセプトロンで表現したコードと実行例は「PythonでパーセプトロンのANDゲートを実装する!」で詳細を書いていますので、是非読んでみて下さい。
この記事の最後で通常論理演算ではありえない小数点や負値の入力を試した所、問題なく動作し下図のように境界線を見ることができました。
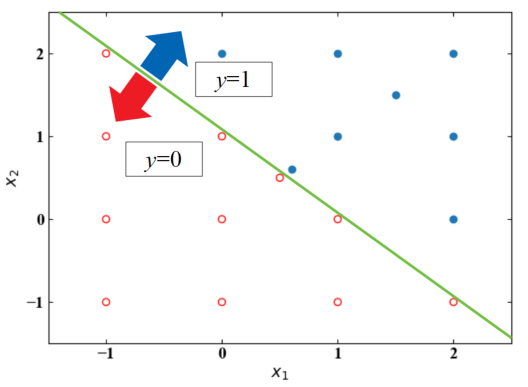
ORゲート
一方ORゲートは下図に示す論理回路です。日本語では論理和と呼ばれます。
真理値表は下表で、入力に1が1つでもあれば1を返します。
| \(x_{1}\) | \(x_{2}\) | \(y\) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
パーセプトロンでORゲートをモデル化したPythonコードは「PythonでパーセプトロンのORゲートを実装する!」という記事に書きましたので、こちらも併せて読んで頂ければと思います。
ANDゲートと似ていますが、パーセプトロンでORゲートを模して計算した値は境界線の位置が異なっている結果を得ました。
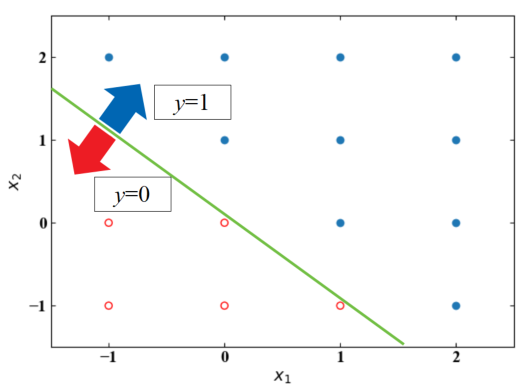
NANDゲート
上記2つの論理回路の他に、NANDゲート(NAND:Not AND)呼ばれるものもあります。これは日本語で否定論理積と呼ばれるもので、ANDゲートで得られた値を否定、つまりANDゲートで0であれば1、ANDゲートで1であれば0を返すというものです。
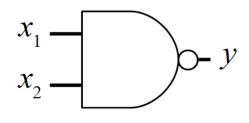
出力の手前にポッチがありますが、これがNotを意味します。
真理値表は下表です。なんともひねくれたやつという印象です。
| \(x_{1}\) | \(x_{2}\) | \(y\) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
このNANDゲートもパーセプトロンで表現することができます。
上で紹介した2つの記事と同じように、Pythonコードで書くと以下のように書けます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
import numpy as np # 2入力パーセプトロンの関数 def perceptron(x1, x2, w1, w2, theta): f = w1 * x1 + w2 * x2 if f <= theta: y = 0 else: y = 1 return y x1 = np.array([0, 0, 1, 1]) x2 = np.array([0, 1, 0, 1]) w1 = -0.8 # 重みw1を入力 w2 = -0.8 # 重みw2を入力 theta = -0.9 # 閾値θを入力 for i in range(4): X1 = x1[i] X2 = x2[i] y = perceptron(X1, X2, w1, w2, theta) print(y) |
このコードを実行すると以下の結果がコンソールに表示されます。
|
1 2 3 4 |
1 1 1 0 |
コードは過去記事のものとまったく同じで重み\(w_{1}\), \(w_{2}\)と閾値\(\theta\)が異なるだけです。他の入力値を入れて詳細なグラフを描いてみるとANDやORと同じようにある場所に境界線が位置し、0と1で分類できていることを確かめられますので、是非可視化にトライしてみて下さい。
線形分離可能な問題以外は対応できない理由
ここまででAND/OR/NANDゲートを見事表現できてきたパーセプトロンですが、お気づきのように分類に使われている境界線は全て直線です。
直線で分類可能な問題のことを線形分離可能と表現しますが、直線しか表現できないことが単一パーセプトロンが線形分離可能な問題以外は対応できない最大で唯一の理由となります。
ダメじゃん!
…と諦めないのが科学者なので、このパーセプトロンをさらに沢山繋げた多層パーセプトロンというモデルが考案されました。
多層パーセプトロンの概要
多層パーセプトロンとは?
多層パーセプトロン(MLP:Multi-Layer Perceptron)とは、本記事の最初に示した単一のパーセプトロンを複数繋げたものです。
多層パーセプトロンの例を下図に示します。
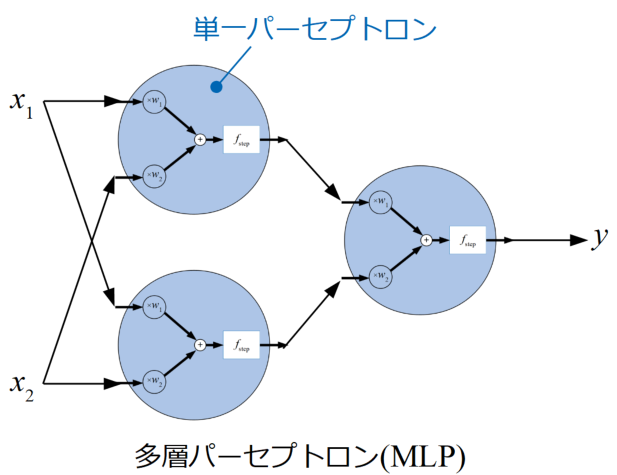
ここで示している多層パーセプトロンは2入力の場合ですが、入力が増えても入力数分の接続数が増えるだけで考え方は同じです。
先ほどまでは直線でしか分類ができない単純なパーセプトロンも、このように複数使うことで複雑な分類が可能になってきます。
なぜ多層にすることで線形以外の識別が可能になる?
線形分類不可能な問題の例:XORゲート
パーセプトロンを多層にすることで、線形分離不可能な問題に対応することができますが、これまで論理回路でパーセプトロンを学んできたので、同じく論理回路を例にした方がその仕組みを理解しやすいと思われます。
以下の図はXORゲート(XOR:Exclusive OR)と呼ばれる論理回路で、日本語では排他的論理和と呼びます。
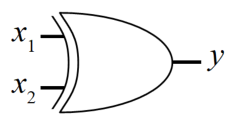
XORゲートの真理値表は下表です。一方が1で、もう一方が0の時だけ1となるゲートということがわかります。
| \(x_{1}\) | \(x_{2}\) | \(y\) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
グラフにプロットすると以下のようになります。この2種類の出力を1本の直線で分類しようとするのは無理ということは自明と言えます。
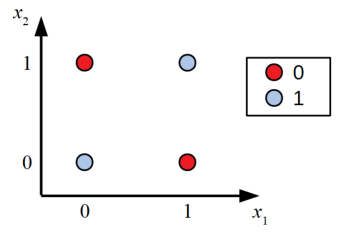
つまり、「XORゲートは単一のパーセプトロンでは表現できない」ということですね!
XORゲートを多層パーセプトロンで表現する方法
XORゲートは単一のパーセプトロンでは表現できませんが、論理回路の分野では複数の論理回路を組み合わせればXORを構築することができるということが古くから知られています。
色々なパターンがありますが、シンプルなものは以下の図に示すようにNAND、OR、ANDを組み合わせたものが有名です。
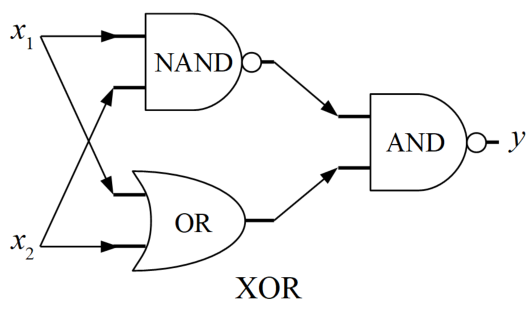
上図の\(x_{1}\)と\(x_{2}\)に値を代入し、真理値表を作っていったものが下表です。最終的な出力である\(y\)の部分では見事XORゲートで欲しかった出力になっています。
| \(x_{1}\) | \(x_{2}\) | NAND | OR | AND(\(y\)) |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
ここで、NANDやOR,ANDゲートはそれぞれ単一のパーセプトロンで表現可能でした。つまり、パーセプトロンを複数使うことで線形分離不可能な問題にも対応できるということの証明にもなっています。
それではPythonによる多層パーセプトロンによるXORゲートの実装コードを書いていきましょう。
Pythonによる多層パーセプトロンコード
全コード
以下が全コードですが、パーセプトロンで書いたNANDゲート、ANDゲート、ORゲートを予め関数で用意しておき、先ほどの複合論理回路で示したようにNANDの出力とORの出力をANDの入力に使用することでパーセプトロンを多層に繋げるということを表現しています(for文の中)。
重み\(w\)や閾値\(\theta\)は既にdef文で書かれた関数の中に決め打ちで記載してあります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
import numpy as np # パーセプトロンによるANDゲート def ANDgate(x1, x2): f = 1.0 * x1 + 1.0 * x2 if f <= 1.0: y = 0 else: y = 1 return y # パーセプトロンによるORゲート def ORgate(x1, x2): f = 0.5 * x1 + 0.5 * x2 if f <= 0.2: y = 0 else: y = 1 return y # パーセプトロンによるNANDゲート def NANDgate(x1, x2): f = -0.8 * x1 + -0.8 * x2 if f <= -0.9: y = 0 else: y = 1 return y x1 = np.array([0, 0, 1, 1]) x2 = np.array([0, 1, 0, 1]) for i in range(4): X1 = x1[i] X2 = x2[i] y1 = NANDgate(X1, X2) y2 = ORgate(X1, X2) y3 = ANDgate(y1, y2) print(y3) |
実行結果
実行結果は以下です。y3が最終的な出力ですが、XORゲートの出力となっていることがわかります。
|
1 2 3 4 |
0 1 1 0 |
入力の範囲と分解能を変えて網羅的に見てみるコード
ANDゲートやORゲートの記事の時もやりましたが、0と1以外の入力を入れてみた時にどういう振る舞いをするか見てみましょう。
「Python/matplotlib3Dプロット!面と散布図を作成」という記事で3D散布図の描き方を習得したので、グリッド軸を用意すれば簡単に入力の範囲を広げたり分解能を細かくしたりが可能であることがわかりました。
今回は3D散布図を使って網羅的に2入力に対する多層パーセプトロンの応答を見てみようと思います。
以下が全コードです。3Dプロットの方法は先に紹介した記事に記載している通りですが、まずx1, x2の軸を用意してnp.meshgridを使ってグリッド軸を作成する所が特徴です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D # パーセプトロンによるANDゲート def ANDgate(x1, x2): f = 1.0 * x1 + 1.0 * x2 if f <= 1.0: y = 0 else: y = 1 return y # パーセプトロンによるORゲート def ORgate(x1, x2): f = 0.5 * x1 + 0.5 * x2 if f <= 0.2: y = 0 else: y = 1 return y # パーセプトロンによるNANDゲート def NANDgate(x1, x2): f = -0.8 * x1 + -0.8 * x2 if f <= -0.9: y = 0 else: y = 1 return y x1 = np.arange(-2.2, 2.2, 0.1) # x1軸を作成 x2 = np.arange(-2.2, 2.2, 0.1) # x2軸を作成 X1, X2 = np.meshgrid(x1, x2) # x1軸とx2軸からグリッドデータを作成 # 多層パーセプトロンの計算をグリッドで実行 Y = np.zeros((len(X1), len(X2))) for i in range(len(X1)): for j in range(len(X2)): out1 = NANDgate(X1[i, j], X2[i, j]) out2 = ORgate(X1[i, j], X2[i, j]) Y[i, j] = ANDgate(out1, out2) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') # データプロットする。 ax1.scatter3D(X1, X2, Y) # グラフを表示する。 plt.show() plt.close() |
実行結果
以下が実行結果です。
細かく見てみると[0,1]、[1,0]以外にも1を返す入力変数の組み合わせがあることがよくわかりました。
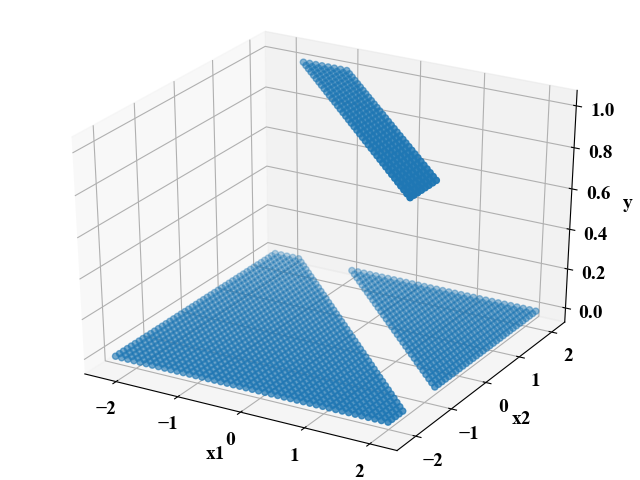
1つだけの単純パーセプトロンではある境界で0と1が分かれていただけでしたが、今回の多層具合だとある範囲を1とするような分類の方法がとれるということみたいです。
まとめ
本記事はおさらいとして、ANDゲートやORゲート、NANDゲートをパーセプトロンで表現する方法を紹介しました。
そしてたった一つだけの単純パーセプトロンでは線形分離可能な問題しか対応できないことを学びましたが、同時に複数のパーセプトロンを組み合わせることでその壁を突破できることをXORゲートの仕組みから理解しました。
最後に、Pythonによる多層パーセプトロンのコードを紹介し、0と1以外の入力に対する応答を確認しました。
結果、今回の多層パーセプトロンはある範囲で0と1を分類できる識別器として作用していることがわかりました。
多層パーセプトロンでも組み合わせ次第で色々な分類問題に対応できそうですね!しかしまだ重みや閾値は決め打ちしているだけですので、これからどんどん先に進んで行きましょう!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント