Pythonでカーブフィット!最小二乗法で直線近似する方法

実験結果等の様々な誤差を含む点列データは通常折れ線グラフでは描かず、そのまま点を散布図で示すか、適切にカーブフィットした直線、または曲線で近似する手法をよくとります。ここではPythonで代表的な最小二乗法による直線近似を行う方法を紹介します。

最小二乗法は技術者必携の道具

最小二乗法とは？折れ線グラフではダメな理由

最小二乗法とは、カーブフィットによる近似手法の1つです。

学生の時に一度は聞いたこと、やったことがある方も多いと思いますが、ここでは少しだけ復習をしていきます。てっとり早くコーディングを見たい方は下にスクロールしてみて下さい！

今ではExcelでグラフを描き、「近似曲線の追加」から自動的に直線近似や多項式近似が出来てしまいますが、今回扱う内容はそれと同じです。

まず、サンプルとして今回扱うデータを見てみましょう。

以下の画像は、ある\(x\)における応答\(y\)をプロットした実験データです。

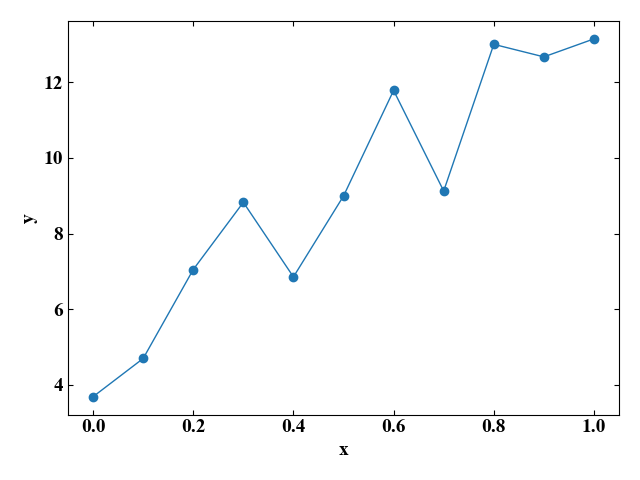
あえて折れ線グラフで描いていますが、これだと単にデータを並べただけで、その後のことは考えていません。

データを並べたその後

実験等でデータを測定した場合、そこには測定器の誤差、実験機器セットアップ起因の誤差、環境の誤差、データロガーの誤差…と様々な誤差を含んでいます。

一般的に、実験をするということは、事前に何かしらの理論式や推定した式を用意してあるはずです。

実験して得られたデータを並べた後は、「その理論式に対して得られたデータがどうか」や、「理論式は微分するとこうなるけど、実験結果はどうか」と検討し、差異がある場合はその理由を考察することで次のアクションへつなげることが出来ます。

では上で示した折れ線グラフで微分形の検討ができるかというと、なかなか難しいですね。

折れ線グラフは「とりあえず」データをプロットするだけなら良いですが、その後の検討がしにくい所がダメな部分です。

回帰直線を使えばパラメータ検討ができる

今回最小二乗法で導くのは以下のグラフの直線です。

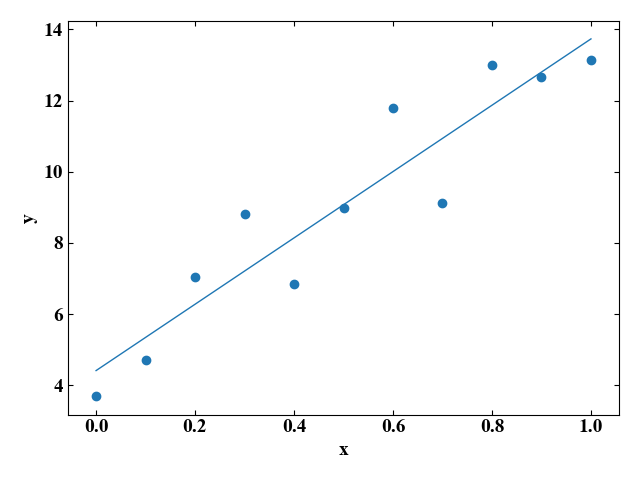
先ほどの折れ線グラフに比べ、こちらの方が\(x\)の増加に伴い\(y\)も増加していく様子が明確に伝わっていますね。

この直線を描くためには、直線の方程式\(y=ax+b\)を求める必要があります。

最小二乗法で直線近似するとは、この直線の方程式の\(a\)と\(b\)を求めることになります。

そしてこれらのパラメータがわかると、微分したりパラメータスタディをしたり、各係数がどんな物理量で構成されているのか、メカニズム検討といったアクションにもつなげることができます。

では続いて最小二乗法の式について説明していきましょう。

最小二乗法による直線近似の式を導出してみよう

データの各要素に名前を付ける

今回行う直線近似は、以下の図に示すように直線\(y=ax+b\)を求めることですが、各データポイントとの誤差を最小にするというのがキーポイントです。

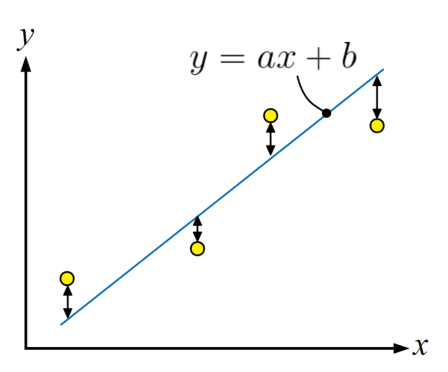
「各データポイントとの誤差を最小にする」を行うために、まずはグラフ上の各要素に名前を付けてみましょう。

各データポイントを\((x_{i}, y_{i})\)の形で座標表現し、点と直線の縦軸値との差を誤差\(\varepsilon_{i}\)と定義します。今回は4つのデータポイントがあるので、\(i\)は1~4となります。

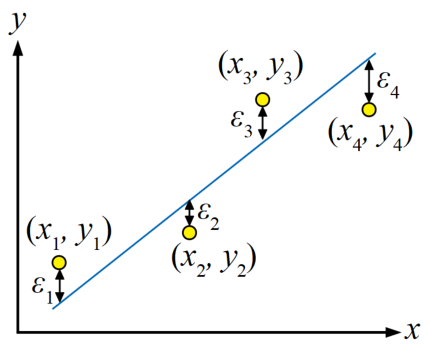
誤差を式で表現する

データの各要素に名前を付けたら、いよいよ式を書くことができます。

まずは誤差を式で表現してみましょう。

誤差\(\varepsilon\)は、\(i\)を使って一般系で書くと、式(1)となります。

$$\varepsilon_{i}=y_{i}-\left ( ax_{i}+b \right )　(1)$$

データポイントの縦軸値\(y_{i}\)と、同じ横軸値\(x_{i}\)を直線の式に代入した時の縦軸値の差、という意味です。

誤差を二乗する

最小二乗法という言葉には「二乗」という文字が入っていますが、これは誤差を二乗する操作がこの方法のキーポイントだからです。

誤差の二乗とはつまり式(2)です。

$$\varepsilon_{i}^{2}=\left \{ y_{i}-\left ( ax_{i}+b \right ) \right \}^{2}　(2)$$

この後、各データポイント毎の誤差の総和をとった数値を最小化するわけですが、二乗することで誤差が全て正の値になるようにすることができます。

最小化する対象に負の値があると、近似した直線はグラフのどん底に落っこちてしまったり、別途複雑な場合分けが必要となり面倒です。

誤差の総和を定義する

誤差を数式で表現し、二乗にする操作をしました。目標は誤差の二乗の総和を最小にすることです。まずは「誤差の二乗の総和」という言葉を式にすると式(3)となります。データ点数が\(n個\)として総和\(S\)を定義しました。

$$S=\sum_{i=1}^{n} \left \{ y_{i}-\left ( ax_{i}+b \right ) \right \}^{2}　(3)$$

式(3)のままの方が本質がわかりやすい形をしていますが、これから微分をするため、中身を展開していき式(4)を得ます。ただ展開しているだけです。

\[
\begin{align}
S&=\sum_{i=1}^{n} \left \{ y_{i}-\left ( ax_{i}+b \right ) \right \}^{2} \\
&=\sum_{i=1}^{n}(y_{i}^{2}-2(ax_{i}+b)y_{i}+(ax_{i}+b)^{2})\\
&=\sum_{i=1}^{n}(y_{i}^{2}-2ax_{i}y_{i}-2by_{i}+a^{2}x_{i}^{2}+2abx_{i}+b^{2})　(4)
\end{align}
\]

\(a\)で偏微分する

式(4)を\(a\)で微分し、式(5)を定義します。この変形は高校くらいで習う微分の公式がわかっていれば簡単ですね。

式(4)は\(a\)の他にも\(b\)という変数がありますが、ここでは\(b\)を固定して\(a\)で微分しているので、偏微分をしていることになります。偏微分なので微分記号は\(\partial\)（パーシャルまたはラウンド）を使っています。

$$\frac{\partial S}{\partial a}=\sum_{i=1}^{n}(2ax_{i}^{2}+2bx_{i}-2x_{i}y_{i})= 0　(5)$$

そして式(5)は「=0」としていますが、これは微分して0になる、すなわち「傾きが0」の部分を求めていることになります。式(4)が\(a\)と\(b\)の二次方程式になっており、二乗項が正の係数なので式(4)は下に凸の放物線です。つまりこの式(5)は放物線が最小値をとるパラメータ\(a\)の値を求めていることになります。

式(5)を式(6)と変形させます。全体を2で割っています。

$$a\sum_{i=1}^{n} x_{i}^{2}+b\sum_{i=1}^{n}
x_{i}-\sum_{i=1}^{n}x_{i}y_{i}=0　(6)$$

\(b\)で偏微分する

今度は式(4)を\(b\)で微分し、こちらも「=0」と置き、放物線が最小値となるパラメータ\(b\)を求める式(7)を立てます。

$$\frac{\partial S}{\partial b}=\sum_{i=1}^{n}( 2ax_{i}+2b-2y_{i})= 0　(7)$$

意味合いは\(a\)の時と同じです。

式(7)も以下の式変形を行って式(8)を得ます。こちらも簡単化のため両辺を2で割っています。

\[
a\sum_{i=1}^{n}x_{i}+bn-\sum_{i=1}^{n}y_{i}=0\\
\frac{a}{n}\sum_{i=1}^{n}x_{i}+b-\frac{1}{n}\sum_{i=1}^{n}y_{i}=0　(8)
\]

これで準備は完了です。続いて\(a\)と\(b\)を求めていきましょう。

連立方程式を立てて\(a\)と\(b\)を求める

いよいよ直線を決定する各パラメータを求めていきます。

\(a\)と\(b\)についてそれぞれ偏微分した式(6)と式(8)を連立させ、式(9)とします。

\[
\begin{eqnarray} \left\{ \begin{array}{l}
a\sum_{i=1}^{n} x_{i}^{2}+b\sum_{i=1}^{n}
x_{i}-\sum_{i=1}^{n}x_{i}y_{i}=0 \\
\frac{a}{n}\sum_{i=1}^{n}x_{i}+b-\frac{1}{n}\sum_{i=1}^{n}y_{i}=0 \end{array} \right. \end{eqnarray}　(9)
\]

ここで、\(b\)はすぐ式(10)と求めることができます。

$$b=\frac{1}{n}\sum_{i=1}^{n}y_{i}-\frac{a}{n}\sum_{i=1}^{n}x_{i}　(10)$$

ここで、式(10)にある\(y_{i}\)の総和を\(n\)で除したものはデータポイントの縦軸値の平均を意味するので、式(11)と書くことができます。

$$\bar{y}=\frac{1}{n}\sum_{i=1}^{n}y_{i}　(11)$$

同様に、式(10)にある\(x_{i}\)の総和を\(n\)で除したものはデータポイントの横軸値の平均を意味するので、式(12)と書くことができます。

$$\bar{x}=\frac{1}{n}\sum_{i=1}^{n}x_{i}　(12)$$

式(11)と式(12)を用いて式(10)を書き直すと式(13)を得ることができます。

$$b=\bar{y}-a\bar{x}　(13)$$

\(b\)を求めることができましたので、式(13)を連立方程式の第1式（つまり式(6)）の\(b\)に代入します(式(14))。

$$a\sum_{i=1}^{n} x_{i}^{2}+(\bar{y}-a\bar{x})\sum_{i=1}^{n}x_{i}-\sum_{i=1}^{n}x_{i}y_{i}=0　(14)$$

ここから先は式変形になります。念のため僕なりの展開を載せますが式番号を付けません。（数学はどちらかといえば得意でないので我流が入っているかも？）

$$a\sum_{i=1}^{n} x_{i}^{2}+\bar{y}\sum_{i=1}^{n}x_{i}-a\bar{x}\sum_{i=1}^{n}x_{i}-\sum_{i=1}^{n}x_{i}y_{i}=0$$

$$a\sum_{i=1}^{n} x_{i}^{2}-a\bar{x}\sum_{i=1}^{n}x_{i}=\sum_{i=1}^{n}x_{i}y_{i}-\bar{y}\sum_{i=1}^{n}x_{i}$$

$$\frac{1}{n}a\sum_{i=1}^{n} x_{i}^{2}-\frac{1}{n}a\bar{x}\sum_{i=1}^{n}x_{i}=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\frac{1}{n}\bar{y}\sum_{i=1}^{n}x_{i}$$

$$\frac{1}{n}a\sum_{i=1}^{n} x_{i}^{2}-a\bar{x}^{2}=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\bar{x}\bar{y}$$

$$a(\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}-\bar{x}^{2})=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\bar{x}\bar{y}$$

ここまで変形できれば、後は式(15)と\(a\)を求めることができます。

$$a=\frac{\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\bar{x}\bar{y}}{\frac{1}{n}\sum_{i=1}^{n}x_{i}^{2}-\bar{x}^{2}}　(15)$$

以上の式(13)と式(15)で回帰直線の方程式\(y=ax+b\)に必要なパラメータ\(a\)と\(b\)をデータポイントの情報から決定することができました。

Pythonで最小二乗法による直線近似をするコード

NumPyのpolyfitが使いやすい！

実はこの記事を書いている途中でNumPyのpolyfitという大変便利な関数があることを発見しました。

そして、polyfit関数を使えば先ほどまでの長い式は全く使わなくなります。

それでは早速コードを紹介します。

今回はcsvからデータを読み込んでいます。コード内のコメントで十分説明できてしまっているくらい簡単ですね。

csvファイルはこんな感じです。

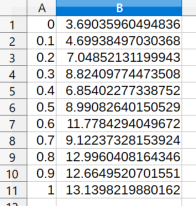
コードは例によってグラフ設定の部分が長いですが、それはご愛敬。

実行結果として、まず直線の傾き\(a\)と\(y\)切片\(b\)を表示します。

グラフは記事冒頭で紹介したものと同じですが、良い感じに線が引かれていますね。

おまけ：真面目に式を関数にしてみる

せっかく式を導出したので、あえて車輪の再発明をしてみます。

直線のパラメータは桁数の違いはありますが、polyfitで求めた場合と同じですね。

まとめ

本記事では、最小二乗法の利用価値と回帰直線を決定するパラメータを導出する方法を紹介し、Pythonによるコーディング方法を示しました。

特にNumPyのpolyfitであればものすごく簡単に回帰直線を決定することが出来ました。