ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
ニューラルネットワークは本来多層を形成して機能させるものですが、多層のメリットや原理を理解するために、一層のパーセプトロンと呼ばれるアルゴリズムで基本的なAND回路を学びます。
こんにちは。wat(@watlablog)です。
ディープラーニングを理解するために、まずはパーセプトロンを学びます。
ここでは論理回路の1つであるAND回路をパーセプトロンで実装します。
パーセプトロンについては様々なWebページで紹介がされていますが、本記事は「斎藤康毅, ゼロから作るDeep Learning, オライリー・ジャパン, (2016), pp.21-27」で学んだ内容を元に、自分なりのコーディングをした結果をまとめています。式の解釈等詳細は書籍をご参照下さい。
パーセプトロンはニューラルネットワークの起源
パーセプトロンとは？
パーセプトロン（Perceptron）とは、1958年にフランク・ローゼンブラッドが論文を発表してから爆発的なニューラルネットワークのブームを巻き起こしたアルゴリズムです。
パーセプトロンのモデルは以下の図のように複数の入力\(x\)と重み\(w\)(ここでは2入力)、1つの出力\(y\)、間にステップ関数と呼ばれる「信号を流すか流さないか」を決める関数があります。
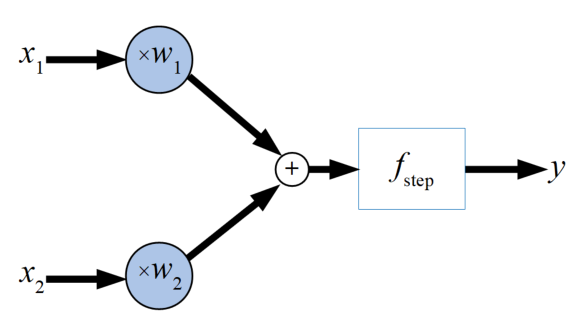
既に「ディープラーニングにおける活性化関数をPythonで作る！」で取り上げたように、このステップ関数は活性化関数です。
ステップ関数は閾値\(\theta\)で信号を流す（1）か流さない（0）かを決めます。モデル全体を式にすると以下の式になります。
\[
y = \begin{cases}
0 & (w_{1}x_{1}+w_{2}x_{2})\leq \theta \\
1 & (w_{1}x_{1}+w_{2}x_{2})> \theta
\end{cases}
\]
後の1969年にマービン・ミンスキーらによってこのパーセプトロンのアルゴリズムは線形分離可能な問題しか学習できないことが指摘されてしまいました。
しかしながらこのパーセプトロンが今日のニューラルネットワークの基礎になっているとのことで、本ページではその基礎を単純なANDゲートを使って学びます。
ANDゲートとは？
ANDゲートとは、論理回路の1つで「論理積」を意味します。図にすると以下のかまぼこのような形状のものです。このような論理回路が我々の使っているコンピュータの中に沢山入っています。
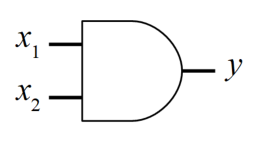
このANDゲートは\(x_{1}\)と\(x_{2}\)がそれぞれ0と1の値で入力された時に、両方とも1の時のみ出力\(y\)が1を出す回路です。以下の表がANDゲートの真理値表です。
| \(x_{1}\) | \(x_{2}\) | \(y\) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
この辺は中学校や高校でやった気がするぞ！
Pythonを始めとしたプログラミング言語では、このような論理計算は標準で演算する関数が用意されていますが、今回はこのANDゲートをあえてパーセプトロンを使って実装することでアルゴリズムの理解を深めます。
ANDゲートのコーディング
Python標準の論理演算機能
まずはPythonに標準に備わっている論理演算子andを使ってANDゲートを書いてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np x1 = np.array([0, 0, 1, 1]) x2 = np.array([0, 1, 0, 1]) for i in range(4): y = x1[i] and x2[i] #PythonのAND演算 print(y) >0 >0 >0 >1 |
入力を4つ用意し、それぞれ論理積を計算すると真理値表の通りの値が算出されますね。
パーセプトロンでコーディング
ではいよいよパーセプトロンの式でANDゲートを書いてみましょう。def文の中身がパーセプトロンの考え方でコーディングした関数です。
本文には重み\(w1\)と\(w2\), \(theta\)にそれぞれ1が入っていますが、これはANDゲートの動作をするように手動で調整した値です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np #2入力パーセプトロンの関数 def perceptron(x1, x2, w1, w2, theta): f = w1 * x1 + w2 * x2 if f <= theta: y = 0 else: y = 1 return y x1 = np.array([0, 0, 1, 1]) x2 = np.array([0, 1, 0, 1]) w1 = 1 #重みw1を入力 w2 = 1 #重みw2を入力 theta = 1 #閾値θを入力 for i in range(4): X1 = x1[i] X2 = x2[i] y = perceptron(X1, X2, w1, w2, theta) print(y) >0 >0 >0 >1 |
重みと閾値の値を別の値にすると全て0になったり異なる動作をしますが、ANDゲートの役割を持たせるパラメータは沢山（無限？）あります。
さらに入力範囲を拡張してみる
論理回路は0（False）か1（True）でしか入力しませんが、いじわるをして今回作ったパーセプトロン関数に負の値を入れたり2を入れたり、小数点を入れたりして特性を見てみましょう。
以下が結果です。わかりやすくするために、\(y=0\)と\(y=1\)でプロットの種類を分けています。
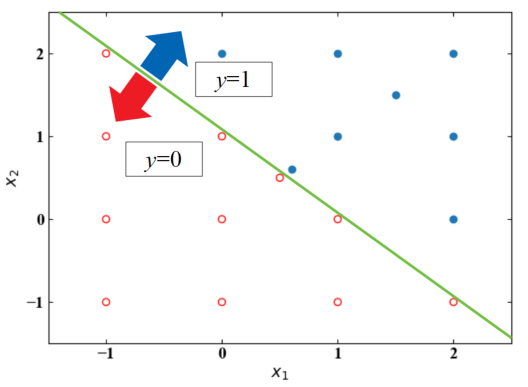
2入力のパーセプトロンで最初はANDゲートに対応させた入力に対する応答を確認し、Python標準のANDゲートと比較をしていましたが、どうやらパーセプトロンの真の意味はこのような線形分類にあるようです。
冒頭で述べたマービン・ミンスキーらの指摘に関係するね。
この線形分類を曲線で分類できるような方法…という所に1960年代以降の知恵が追加されたと予想しているけど、どうなんだろ？
学習を進めればその辺の背景もクリアになるかな？
上図を算出するPythonコードを念のため以下にメモしておきます。
\(y\)が0の時と1の時で場合分けして配列にそれぞれ座標値を格納するだけで、簡単に色分けしたプロットを描くことができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
import numpy as np from matplotlib import pyplot as plt #2入力パーセプトロンの関数 def perceptron(x1, x2, w1, w2, theta): f = w1 * x1 + w2 * x2 if f <= theta: y = 0 else: y = 1 return y x1 = np.array([0, 0, 1, 1, 0, 1, -1, -1, -1, 2, 0, 2, 1, 2, -1, 2, 0.5, 0.6, 1.5]) x2 = np.array([0, 1, 0, 1, -1, -1, 0, -1, 1, 0, 2, 1, 2, 2, 2, -1, 0.5, 0.6, 1.5]) w1 = 1 w2 = 1 theta = 1 #プロット用の配列（P0がy=0, P1がy=1の座標を入れるための配列） P0_x = [] P0_y = [] P1_x = [] P1_y = [] #プロット用にデータを分類し格納する。 for i in range(19): X1 = x1[i] X2 = x2[i] y = perceptron(X1, X2, w1, w2, theta) print(y) if y == 0: P0_x.append(x1[i]) P0_y.append(x2[i]) else: P1_x.append(x1[i]) P1_y.append(x2[i]) P0_x = np.array(P0_x) P0_y = np.array(P0_y) P1_x = np.array(P1_x) P1_y = np.array(P1_y) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('$x_{1}$') ax1.set_ylabel('$x_{2}$') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(-3, 3, 1)) ax1.set_yticks(np.arange(-3, 3, 1)) ax1.set_xlim(-1.5, 2.5) ax1.set_ylim(-1.5, 2.5) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.scatter(P0_x, P0_y, facecolors = 'none', edgecolors = 'r', label='$y=0$', lw=1) ax1.scatter(P1_x, P1_y, label='$y=1$', lw=1) fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
<広告>
人工知能のプロに最速でなるには、独学よりも効果的なオンラインゼミがあります。これを機会に是非ご検討下さい！
まとめ
本ページでは簡単な論理回路を使ってパーセプトロンモデルをPythonを使って記述してみました。
0と1だけの入力は式の重み\(w\)と閾値\(\theta\)を調整することで実際のANDゲートと同じ動作をすることがわかりました。
しかし入力値を実数に拡張すると、どうやらこのパーセプトロンモデルは値を実数全体で線形に分離する役目があることがわかりました。
ディープラーニングの学習の前にニューラルネットワークの基礎であるパーセプトロンを学習しました。
関数を通った後の出力値を見ると、今後色々な問題を分析できそうな気がしてきましたね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント