
今すぐ、何も考えず、とにかくcsvに記録したデータを周波数分析したい人向。ここではPythonとIDEのインストール、プログラム実行方法のおさらいの後に、デモcsvファイルとコピペ動作するフーリエ変換コードを紹介して目的を最速達成します。
こんにちは。wat(@watlablog)です。ここでは"Python何もワカラン"な人が爆速でフーリエ変換できるようになる方法を紹介します!
この記事の対象者
とにかくフーリエ変換したい人
この記事は、「細かい事は良い!とにかく爆速でフーリエ変換がしたいんだ!」という方を対象としています。
明日までに客先にこの実験データの周波数分析を報告しないといけないんだ!
教授から「フーリエ変換しといて!」って言われた!授業寝ていたから出来ませんなんて言えないよ…!
…という人々の救いの手になればと思い記事化しました(あわよくばPython使いを増やしたい…という裏の目的もありますが)。
フーリエ変換って何なのか、理論を知りたい人や、軸の意味、オーバーラップを使った平均化フーリエ変換、窓関数の使い方、スペクトログラム等の応用の計算を知りたい人は対象にしていません。
もうちょっとフーリエ変換の内容や色々な派生処理を細かく知りたい人はUターンする必要はありません。
是非「PythonでFFT実装!SciPyのフーリエ変換まとめ」をご覧下さい。このページよりは詳しく書いてあります。
Python全く知らない人
この記事ではPythonというプログラミング言語を使ってフーリエ変換を行います。とにかくフーリエ変換したい人にとって言語はどうでもよいと思いますが、ここでは誰が何と言おうとPythonで行います。
でも安心して下さい。このページでは当ブログでこれまで扱ったPythonのインストール方法の記事リンクから説明しますので、WindowsかMacのPCさえ持っていれば、Pythonに関して全く知識がない人も最後まで読み進める事が出来ます。
さらに、会社等でプロキシ設定に阻まれてライブラリインストール出来ない人も対象にしています。インターネットに接続できて、PyPIにアクセスできれば問題ありません。
もちろん全て無料です。
この記事の目標
csvファイルの複数信号を一度に周波数波形にする
この記事では以下のフォーマットで時間波形が記録されたデータをフーリエ変換します。おそらく色々なデータロガーでcsv出力するとこのような形式で出てくる事でしょう。

1行目はヘッダです。A列に時間[s]、B列以降は各信号の名称でも書いておきます(わかりやすくするためであって、名前は何でも良いです)。
A列はフーリエ変換する分だけの時間軸を用意しておいて下さい。時間刻みは一定(等ピッチ)である必要があります。フーリエ変換後の周波数分解能はこの時間が長いほど細かくなります(時間長の逆数[Hz])。分解能を揃えたり調整したい場合は最終時間を揃えましょう。
B列以降はA列の各時刻に対応した振幅成分(例えば電圧、加速度…といった物理的な波形)を用意します。ファイルが許す限り列方向に信号を並べておいて構いません。
検証済の動作環境
PC
僕は以下のWindows環境、Mac環境で本記事のコードを動作検証しています。Linuxやその他OSは対象としていません。
| Windows | OS | Windows10 64bit |
|---|---|---|
| CPU | 2.4[GHz] | |
| メモリ | 4[GB] |
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
Python環境
この後説明するPython環境に関するバージョン情報は以下表に示す通りです。おそらく最新バージョンでも動くと思いますが、検証したのは下の環境のみ。とにかくはやくフーリエ変換したい場合は揃えておくのが無難かと思います。
PythonはPython本体、PyCharmはプログラムを記述して実行したりデバッグしたりする統合開発環境(IDE)、Numpy・Scipy・Pandas・matplotlibはPythonにインポートして使う便利な外部ライブラリです。
| Python | Python 3.7.7 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.19.0 |
| Scipy | 1.4.1 |
| Pandas | 1.0.5 |
| matplotlib | 3.2.2 |
以上の前置きを確認したら、早速環境構築をしていきましょう!環境が既に構築されている人はコード部分までスクロールして下さい。
環境構築
Pythonのインストール
はじめにプログラミング言語であるPythonをインストールしましょう。
PythonのインストールにはAnacondaを推奨する書籍やサイトが沢山ありますが、2021年現在Anacondaは商用利用に制限がかかっているようです。それ以外にも色々面倒な管理となりそうであるため、筆者はAnacondaを使っていません(いちいちライブラリをインストールするのは面倒ですが)。
インストールの方法はWindowsとMacで以下の記事をご確認下さい。
Windows版:「Pythonのインストール方法とAnacondaを使わない3つの理由」
Mac版:「macOSにPython3をインストールする方法をまとめてみた」
そのうちもっと良い環境構築方法も試してみたいと思います(Dockerとか?)
統合開発環境(IDE)のインストール
コードを打ち込んでプログラムを実行するだけならテキストエディタを使ってコマンドプロンプトやターミナルで実行する方法でも十分ですが、デバッグやコード記述補助機能を利用するためには統合開発環境(IDE)を使うのが良いです。
こちらも以下のWindowsとMacで記事を用意していますので、参照しながらインストールしてみて下さい。
Windows版:「Pythonの統合開発環境(IDE)はPyCharmで良い?」
Mac版:「macOSにPython統合開発環境PyCharmをインストール」
外部ライブラリのpipインストール
pip概要と外部ライブラリのインストール方法
先ほど紹介したNumpyやScipyといった外部ライブラリはpipインストールするのが一般的です。
pipについての概要は「Pythonのパッケージ管理ツール pip の使い方とコマンド集」、Windows版とMac版のコマンドの違いは「独断!Pythonでpipインストールしたい外部ライブラリまとめ」をご確認下さい。
プロキシエラーになる場合
ちゃんとした会社であればもしかするとpipインストール時にプロキシエラーが発生するかも知れません。
PyPIにアクセスできるインターネット環境をお持ちであれば、「pip installでプロキシエラーになる問題を解決する方法」に記載の方法で解決可能です。
こんな事で諦めるのはもったいないです。
csvを離散フーリエ変換するPythonコード
準備するcsvファイル【ダウンロード可】
ここからはいよいよコードを使ってフーリエ変換をしてみます。
まずはサンプルのcsvファイルとして以下の「signals.csv」をダウンロードしてみて下さい。
あとはこのファイルの中身を自分のデータに書き換えて下のコードを実行するだけで目的は達成できるはずです。
ただ、書き換える時はエンコードを「SHIFT-JIS」にする事を忘れずに。もし「UTF-8」で作ってもコードの方を変更すれば大丈夫ですが。
全コード【コピペ・2次利用可】
以下にcsvをフーリエ変換するだけの全コードを示します。このコードを実行するとfft.csvというファイルが生成されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
import numpy as np from scipy import fftpack import pandas as pd import matplotlib.pyplot as plt # フーリエ変換をする関数 def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成 return spectrum, amp, phase, freq # csvから列方向に順次フーリエ変換を行い保存する関数 def csv_fft(in_file, out_file): df = pd.read_csv(in_file, encoding='SHIFT-JIS') # ファイル読み込み dt = df.T.iloc[0,1] # 時間刻み # データフレームを初期化 df_amp = pd.DataFrame() df_phase = pd.DataFrame() df_fft = pd.DataFrame() # 列方向に順次フーリエ変換(DFT)をするコード for i in range(len(df.T)-1): data = df.T.iloc[i+1] # フーリエ変換するデータ列を抽出 spectrum, amp, phase, freq = calc_fft(data.values, 1/dt) # フーリエ変換をする関数を実行 df_amp[df.columns[i+1] + '_amp'] = pd.Series(amp) # 列名と共にデータフレームに振幅計算結果を追加 df_phase[df.columns[i+1] + '_phase[deg]'] = pd.Series(phase) # 列名と共にデータフレームに位相計算結果を追加 df_fft['freq[Hz]'] = pd.Series(freq) # 周波数軸を作成 df_fft = df_fft.join(df_amp).join(df_phase) # 周波数・振幅・位相のデータフレームを結合 df_fft = df_fft.iloc[range(int(len(df)/2) + 1),:] # ナイキスト周波数でデータを切り捨て df_fft.to_csv(out_file) # フーリエ変換の結果をcsvに保存 return df, df_fft # 関数を実行してcsvファイルをフーリエ変換するだけの関数を実行 df, df_fft = csv_fft(in_file='signals.csv', out_file='fft.csv') |
Python上でグラフ表示をしたい時は以下のコードを先ほどのコードの最後にコピペすると、matplotlibによるグラフが表示されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
# ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(121) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(222) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(224) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Phase[deg]') ax3.set_xlabel('Frequency [Hz]') ax3.set_ylabel('Amplitude') # スケールの設定をする。 ax2.set_yticks(np.arange(-180, 181, 90)) ax2.set_ylim(-180, 180) #ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 size = len(df.T)-1 for i in range(size): ax1.plot(df.T.iloc[0], df.T.iloc[i+1], label=df.columns[i+1], lw=1) ax2.plot(df_fft.T.iloc[0], df_fft.T.iloc[i+size+1], label=df_fft.columns[i+size+1], lw=1) ax3.plot(df_fft.T.iloc[0], df_fft.T.iloc[i+1], label=df_fft.columns[i+1], lw=1) ax1.legend() #ax2.legend() ax3.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
実行結果例
生成されたcsvファイルの例を以下に示します。今回はB列に周波数、以降は振幅と位相のデータが最初に指定したデータ数分順番に並びます。
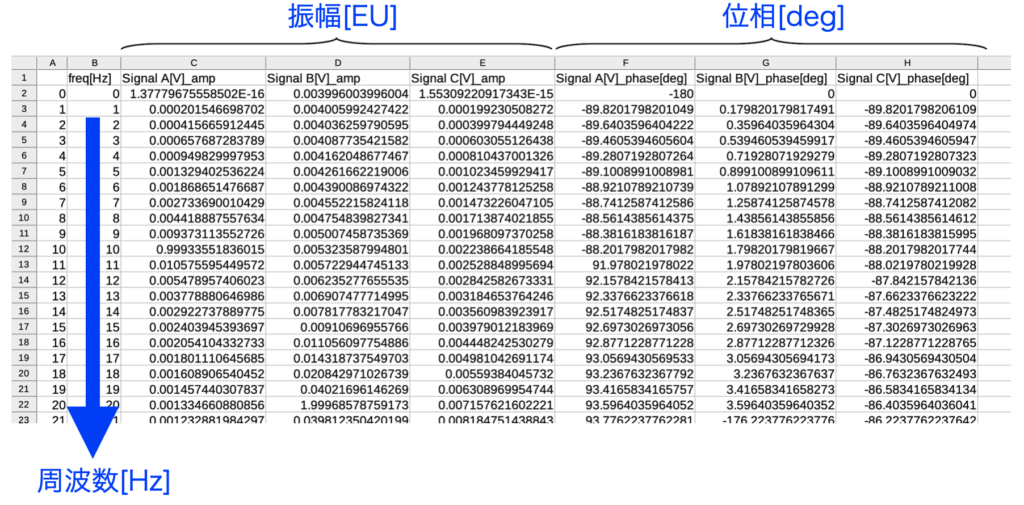
グラフの例は下図です。パッと確認したい時はPython上で見るのが一番ですね。
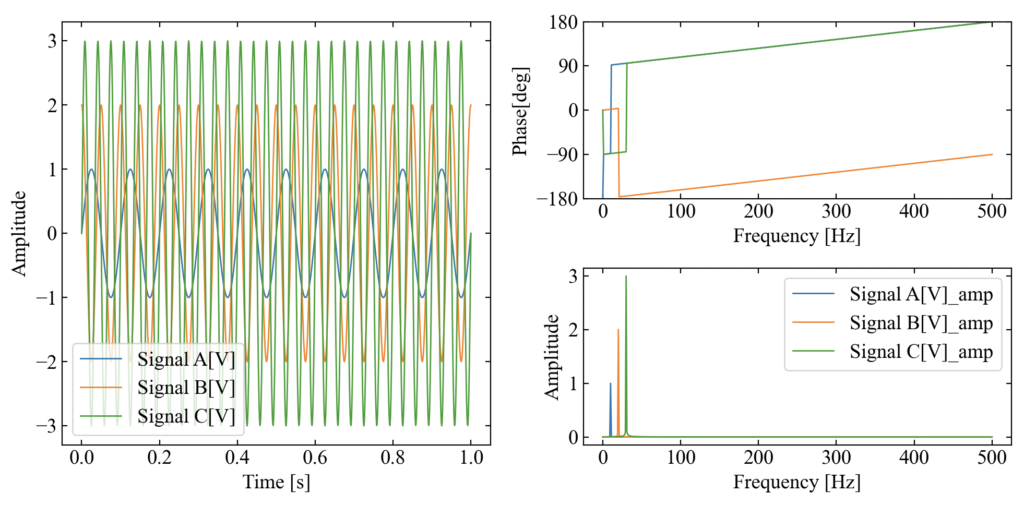
おまけ:csvを平均化フーリエ変換するPythonコード
平均化フーリエ変換のおさらい
ここからはおまけです。当ブログでは「PythonでFFT実装!SciPyのフーリエ変換まとめ」という記事で平均化フーリエ変換のコードを作ってみました。
この章では先ほどまでの1フレームフーリエ変換とは異なり、フレームサイズをプログラム的に決めて、オーバーラップや窓関数をかけながら平均化を行うフーリエ変換をcsvデータに対して行うコードを紹介します。
オーバーラップをかけながら…というのは下図のイメージです。もしこの辺の理解が曖昧であれば先ほど紹介した記事をご覧ください。
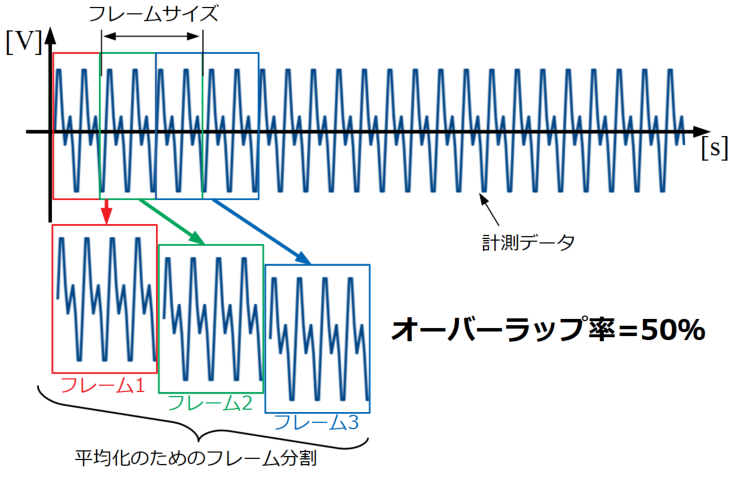
前回の記事をコピペしながら作ったので、もしかしたらバグがあるかも知れません。もし使う場合は自分で十分検証してからの方が良いと思います。
準備するcsvファイル2【ダウンロード可】
csvファイルは先に紹介したものと同じフォーマットです。平均化を必要とする波形という意味で、時間長は長くした方が良いでしょう。
以下は10[s]のホワイトノイズ×3が入ったcsvファイルです。今回のコード検証用に是非ご利用ください。
コード
fft_function.pyファイルの作成
「PythonでFFT実装!SciPyのフーリエ変換まとめ」と同様にメインの.pyとは別にfft_function.pyというPythonファイルを作成します。
このファイルにはオーバーラップや窓関数、フーリエ変換する関数をまとめてあります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import numpy as np from scipy import signal from scipy import fftpack #オーバーラップ処理 def ov(data, samplerate, Fs, overlap): # 全データ長Ts、フレーム周期Fc、オーバーラップずらし位置x_ol Ts = len(data) / samplerate Fc = Fs / samplerate x_ol = Fs * (1 - (overlap/100)) # 抽出するフレーム数(平均化に使うデータ個数) N_ave = int((Ts - (Fc * (overlap/100))) / (Fc * (1-(overlap/100)))) # フレームで時間データを抽出:切り出し位置ps array = [] for i in range(N_ave): ps = int(x_ol * i) array.append(data[ps:ps+Fs:1]) return array, N_ave #窓関数処理(ハニング窓) def hanning(data_array, Fs, N_ave): # ハニング窓 han = signal.hann(Fs) # 振幅補正係数(Amplitude Correction Factor) acf = 1 / (sum(han) / Fs) #オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han return data_array, acf #FFT処理 def fft_ave(data_array,samplerate, Fs, N_ave, acf): fft_amps = [] fft_phases = [] for i in range(N_ave): # フーリエスペクトル、振幅と位相を計算する spectrum = fftpack.fft(data_array[i]) amp = acf * np.abs(spectrum / (Fs/2)) phase = np.degrees(np.arctan2(spectrum.imag, spectrum.real)) fft_amps.append(amp) fft_phases.append(phase) # 周波数軸作成と振幅(パワー平均)と位相の平均化 fft_axis = np.linspace(0, samplerate, Fs) fft_amps = np.array(fft_amps) fft_amp_mean = np.sqrt(np.mean(fft_amps ** 2, axis=0)) fft_phase_mean = np.mean(fft_phases, axis=0) return fft_amps, fft_amp_mean, fft_phase_mean, fft_axis |
メインファイル
以下のメインコードでcsvの読み書きを行います。グラフプロットもしていますが、このコードを実行するとfft.csvに平均化したフーリエ変換の振幅と位相が記録されます。
コードは関数実行部分でフレームサイズFsとオーバーラップoverlapを指定するスタイルです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 |
import fft_function import numpy as np from scipy import fftpack import pandas as pd import matplotlib.pyplot as plt # フーリエ変換をする関数 def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成 return spectrum, amp, phase, freq # csvから列方向に順次フーリエ変換を行い保存する関数 def csv_fft(in_file, out_file, Fs, overlap): df = pd.read_csv(in_file, encoding='SHIFT-JIS') # ファイル読み込み dt = df.T.iloc[0,1] # 時間刻み # データフレームを初期化 df_amp = pd.DataFrame() df_phase = pd.DataFrame() df_fft = pd.DataFrame() # 列方向に順次フーリエ変換(DFT)をするコード for i in range(len(df.T)-1): data = df.T.iloc[i+1] # フーリエ変換するデータ列を抽出 # 平均化フーリエ変換(過去記事からほぼコピペ)----------------- # オーバーラップ抽出された時間波形配列 time_array, N_ave = fft_function.ov(np.array(data), 1/dt, Fs, overlap) # ハニング窓関数をかける time_array, acf = fft_function.hanning(time_array, Fs, N_ave) # FFTをかける fft_array, fft_amp_mean, fft_phase_mean, fft_axis = fft_function.fft_ave(time_array, 1/dt, Fs, N_ave, acf) # -------------------------------- # 列名と共に振幅と位相をデータフレームに追加 df_amp[df.columns[i+1] + '_amp'] = pd.Series(fft_amp_mean) df_phase[df.columns[i+1] + '_phase[deg]'] = pd.Series(fft_phase_mean) # 周波数軸をデータフレームに追加 df_fft['freq[Hz]'] = pd.Series(fft_axis) # データフレーム結合 df_fft = df_fft.join(df_amp).join(df_phase) # ナイキスト周波数でデータ切り捨て df_fft = df_fft.iloc[range(int(Fs/2) + 1), :] # csv保存 df_fft.to_csv(out_file) return df, df_fft # 関数を実行してcsvファイルをフーリエ変換するだけの関数を実行 # 平均化フーリエ変換のパラメータ:Fs=フレームサイズ、overlap=オーバーラップ率[%] df, df_fft = csv_fft(in_file='signals_2.csv', out_file='fft.csv', Fs=1024, overlap=0) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(121) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(222) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(224) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Phase[deg]') ax3.set_xlabel('Frequency [Hz]') ax3.set_ylabel('Amplitude') # スケールの設定をする。 ax2.set_yticks(np.arange(-180, 181, 90)) ax2.set_ylim(-180, 180) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 size = len(df.T)-1 for i in range(size): ax1.plot(df.T.iloc[0], df.T.iloc[i+1], label=df.columns[i+1], lw=1) ax2.plot(df_fft.T.iloc[0], df_fft.T.iloc[i+size+1], label=df_fft.columns[i+size+1], lw=1) ax3.plot(df_fft.T.iloc[0], df_fft.T.iloc[i+1], label=df_fft.columns[i+1], lw=1) ax1.legend() ax2.legend() ax3.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
実行結果の例
以下は実行結果の例です。signals_2.csvにはホワイトノイズ(下図)が記録されており、下図真ん中はFs=10000とほぼ1フレームで計算した場合、下図右はFs=1024、overlap=0で計算した場合です。
フレームサイズを変更する事で周波数分解能に違いが出ている事がわかりますが、これだけでは平均化の効果はあまりわかりません。
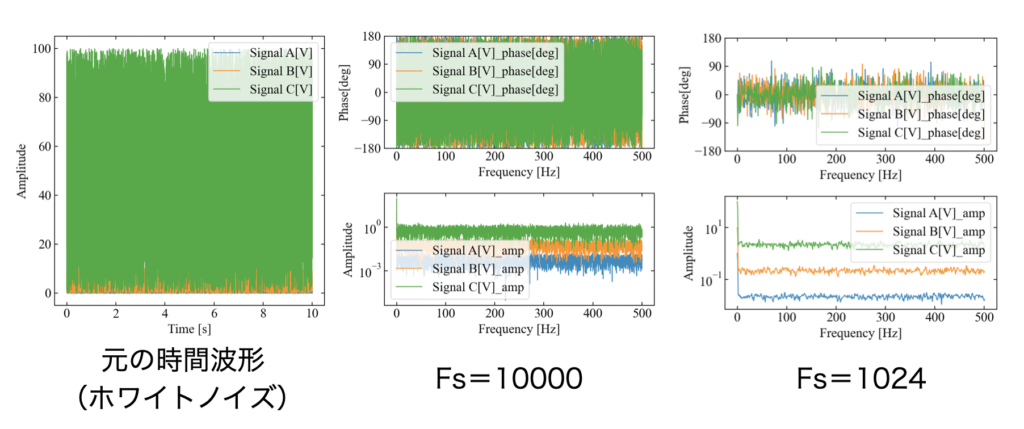
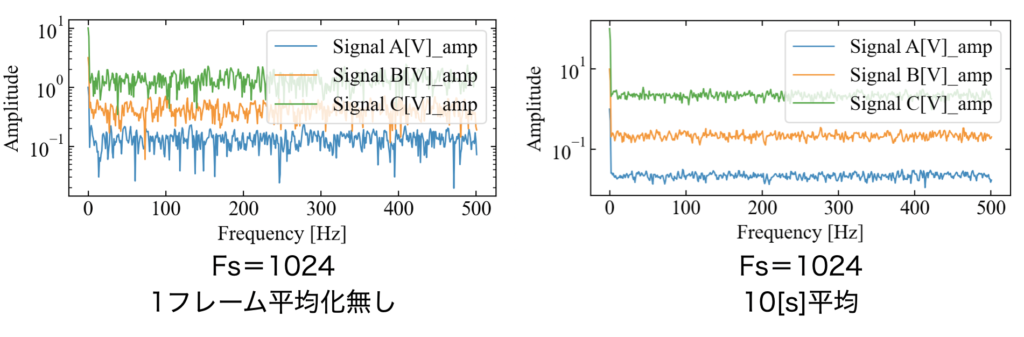
下図は本記事の始めに紹介した1フレームフーリエ変換で時間波形のフレームサイズFs=1024にして計算した場合(左)と、平均化フーリエ変換で10[s]のデータをフレームサイズFs=1024で計算した場合(右)の比較です。
つまり、フレームサイズを統一して周波数分解能を同じにして比較してみました。
右図は雑味が低減している様子が確認できると思います。
おまけは以上。
まとめ
今回は既に過去学んだ事を組み合わせて、「csvファイルをフーリエ変換する」というだけのコードを紹介してみました。
信号処理をExcelのみで実施している人からは、よく「フーリエ変換のやり方教えて!」と質問が来ていました。
この記事を用意しておく事で、ライセンスの必要な高度なソフトを立ち上げて、おまけ機能で付いているフーリエ変換を教えるという事をしなくて済みそうです。
Pythonであればプログラミングのハードルも低いので、これをきっかけに皆さんも「ちょっと何かやる」という用途に是非使ってみて下さい!
関連リンク
以下にcsvファイルの入出力に特化した関連記事をリンクします。是非信号分析業務にお役立て下さい。
csvからデジタルフィルタをかけるコード
ただPythonでcsvからデジタルフィルタをかけるだけのコード
csvから逆フーリエ変換するコード
ただPythonでcsvから逆離散フーリエ変換をするだけのコード
Pythonでフーリエ変換+csvファイル処理を組み合わせてみました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
26行目のdfは何か事前に定義が必要でしょうか。エラーになってしまいます。Pycharmでなくjupyter notebookの環境を使っているのが原因でしょうか。
# 列方向に順次フーリエ変換(DFT)をするコード
for i in range(len(df.T)-1):
ご訪問ありがとうございます。
dfでエラーとの事で、事前にdf = と書いている部分のあとにprint(df)として想定通りのデータが入っていますでしょうか?
エラーメッセージの内容がわかればより推測できそうです。
以上、よろしくお願い致します。
ありがとうございます。print(df)で実行すると、以下のメッセージが出ます。
dfが定義出来ていない、ということだと思うのですが書き方が分からずアドバイスを頂けると嬉しいです。基本的なことですみません。
—————————————————————————
NameError Traceback (most recent call last)
in
—-> 1 print(df)
NameError: name ‘df’ is not defined
NameErrorという事はdf = …という文が実行されていないのかなと思います。
df = pd.read_csv(in_file, encoding=’SHIFT-JIS’)
は実行していますか?
この文の直後にprint(df)を実行すると、csvファイルの中身が見れるはずです。
実行しているとすると、もうちょっと詳しくデバッグしたいですね。
printをこまめに挟みながら原因を探るのがはやいと思いますが、ご検討いただけますでしょうか。
ありがとうございます。41行目にdfの定義がありました。
df, df_fft = csv_fft(in_file=’signals.csv’, out_file=’fft.csv’)
数行ずつ「Restart&All Run」していたのですが、一気にコピーするか、41行目を先に記載する必要がありました。とても分かりやすい記事で次回も楽しみにしています。
ご連絡ありがとうございます。
解決したようでよかったです!
コメント失礼いたします。
フーリエ変換ができずに困っていたため大変役に立ちました,ありがとうございます!
逆フーリエ変換をしたい場合,どこをどう変えればよいでしょうか。
返信お待ちしております。
ご訪問ありがとうございます。
逆フーリエ変換の記事は以下に記載しております。
「https://watlab-blog.com/2019/10/12/fft-ifft/」
本記事のフーリエ変換をする部分で、逆フーリエ変換の関数を作成・使用する事で可能となります。
逆フーリエ変換には複素データが必要な事が注意点です。
どうやら需要がありそうですので、「ただだけシリーズ」としてこちらでも記事化してみようと思います。
以上、よろしくお願い致します。
初めまして。大変わかりやすい解説ありがとうございます。勉強になります。
こちらの記事のようなcsvを読み込ませたFFTで、
https://watlab-blog.com/2019/04/21/python-fft/
こちらのオーバーラップ、窓関数、平均化処理を実装するにはどのようにしたらよいでしょうか?
ご訪問ありがとうございます。
csvに記録した時間長を長くして、フレームに区切って平均化したいという事ですね。
今回こちらの記事ではcsvから時間波形データを1つずつ取り出してフーリエ変換しています。
対してオーバーラップ混みの記事ではサンプルの時間波形dataを使っていましたが、これが時間波形に相当します。
取り出した時間波形に対して「https://watlab-blog.com/2019/04/21/python-fft/」の関数群を適用していけば実現可能と考えます。
こちらでイメージはできましたので、後でこのページの記事に追記しておこうと思います(少し時間はかかりますが…)。
以上、よろしくお願い致します。
初心者の素人質問ですみません。
グラフ表示した際に移送角の表示は必要ないので、生データのグラフとFFT結果を
横並びで同じサイズで表示したいのですが、このプログラムではどのあたりを
修正すればそういった表示が可能でしょうか。
ご訪問ありがとうございます。
位相情報を外したい場合は、ax1(時間波形)とax3(振幅周波数波形)のみを使うことになります。
ax○を全て書き換えて、スリムなコードにしても良いのですが、てっとり早く確認した場合は以下手順で目的の表示が可能です。
■手順
①「ax2.〜」で始まる行をコメントアウト、または削除する。
②「ax3 = fig.add_subplot(122)」と、subplotの数値を122にする。
■解説
subplot()はmatplotlibのプロット配置位置を指定することができます。
111は「全グラフが1行1列で、1番目の位置」を意味し、
122は「全グラフは1行2列で、2番目(つまり右)の位置」を意味します。
以上、回答になりましたでしょうか?
詳しいmatplotlibのsubplot()の使い方はまだ記事を書いていませんが、Google検索で色々出てきますので、調べてみると良いかも知れません。
よろしくお願い致します。
コメント失礼いたします.
pythonで一次元フーリエ変換ができずに困っていた為,とても助かりました,ありがとうございます!
話は変わりますが,二次元フーリエ変換をしたい場合,どう変えればよいでしょうか?
画像を二次元フーリエ変換するのではなく,csvファイルの数値を読み込み,二次元フーリエ変換を行いたいです.横方向にフーリエ変換をした後,縦方向にフーリエ変換する事は分かるのですが,プログラムをどう組めばいいのか分からない状況です.
返信お待ちしております。
ご訪問ありがとうございます。
2DFFTは画像に限った話ではなく、2次元方向に独立な周期性を持つデータ全般に使うことができます。
そのため、以下の記事のようにnp.fft.fft2を使うのが簡単な方法と思います。
「https://watlab-blog.com/2020/03/22/2d-fft/」
ただ、データの素性や分析の目的によっても変わりそうですし、
上記方法でも手持ちのデータの分解能や小数点以下の桁数によっては前処理が必要かも知れません。
いずれにしても、まずは手持ちデータに近い形式で理想波形(横方向、縦方向それぞれで○Hzの正弦波を描いてみる等)を作り、
意図通りの変換が行われているか検証しながらコーディングした方が良さそうです。
ご返信ありがとうございます!
np.fft.fft2のコーディングで上手く作る事が出来ましたありがとうございました!
よかったです!
ご連絡ありがとうございました。
コメント失礼いたします。
上記のようなコードを作成していただきありがとうございます。
現在、csvファイルからpyhtonを用いて離散フーリエ変換を行っているのですが、テストデータとして3つのサイン波を合成させたもので上記のコードを試したのですが、うまく指定した周波数にパルスが立たなくて困っています。横軸や、サンプリング周波数など変えてみましたが、うまく立ちませんでした。
テストデータは、周波数をそれぞれ20Hz、40Hz、70Hzの波を振幅を変えて合成させたものを1msごとに縦に並べました。
ご返信お待ちしております。
ご訪問ありがとうございます。
詳細はまだわかりませんが、csvのフォーマットが間違っていないとすると、以下の結果はいかがでしょうか?
①csvをExcel等でグラフ化してみて、ちゃんとサイン波になっているかどうか。
②csvファイルのエンコードがSHIFT-JISかどうか。
もしUTF-8等であれば、
df = pd.read_csv(in_file, encoding=’SHIFT-JIS’)
の部分を変更する必要があります。
以上、少しずつ検証していけば解決すると思いますので、ご確認いただければと思います。
ご返信ありがとうございます!
少しづつ確認してみます!
はじめまして
Python初心者ですが、こちらの記事を参考にしてフーリエ変換を学んでいます。
csvを平均化フーリエ変換するPythonコードをコピペして実行してみたのですが、33行目のfft_function.ovでエラーが出でしまいます。
エラーの内容としては、AttributeError: module ‘fft_function’ has no attribute ‘ov’
です。
大変恐縮なのですが、この原因を教えていただけないでしょうか?
使用環境は、
Jupyter notebookでPythonを実行しており、
以下のバージョンです。
Python version:3.9.12 (main, Apr 4 2022, 05:22:27) [MSC v.1916 64 bit (AMD64)]
IPython version:8.2.0
Numpy version:1.21.5
scipy version:1.7.3
pandas version:1.4.2
matplotlib version:3.5.1
seaborn version:0.11.2
scikit-learn version:1.0.2
何卒宜しくお願い致します。
ご訪問ありがとうございます。
そのエラーはfft_function.pyの中にovという関数がないということを意味しています。
ここに記載のコードはfft_function.pyの中に各種関数を記述し、main.pyの中でそれらをimportしています。
まずはこのファイル構成が意図したものになっていますでしょうか?
ファイルに分けたくない場合はmain.pyの中に全て記載することも可能ですが、その場合は
fft_function.ov〜→ov〜
とfft_function.を外す必要があります。
以上、まずはご確認お願い致します。
ファイルを分けず、main.pyの中にすべて記載することで解決できました。
ありがとうございました!
ご連絡ありがとうございます。
解決したようで安心しました!
初心者*素人ですが、最初のコードの描画部分の39行目,ax2.plot()内の[]内は、i+size でなく、i+size+1 ではないでしょうか。元のままだと位相のグラフだけおかしくなり、上記のような修正で改善しました。
見当違いだったらすみません。
ご訪問ありがとうございます。
そのとおりですね、ご指摘いただきありがとうございます!
下のコードと同じく+1が抜けていました。
修正いたしました!
こんにちは。素人質問内容なのですが、ダウンロードしたsignalsのcsvのファイルはどこに保存すればよいでしょうか。単純にエクスプローラーのダウンロードに保存すると No such file or directory: ‘signals.csv’とでてプログラムを実行できません。
ご訪問ありがとうございます。そして返信が遅れてしまい大変申し訳ございません!
csvファイルをプログラムからそのまま読むようにするには、プログラムファイルと同じ場所にcsvファイルをおいてください。