2021.08.05

ただPythonでcsvからデジタルフィルタをかけるだけのコード

今すぐ、何も考えず、とにかくcsvに記録したデータに対しデジタルフィルタをかけたい人向け。ここではPythonを知らない人のための導入を説明してから、デモcsvファイルとコピペ動作するフィルタ処理コードを紹介して目的を最速で達成します。

こんにちは。wat(@watlablog)です。ただだけシリーズ、ここではPythonを知らなくてもとにかくデジタルフィルタをかける事ができるようになる方法を紹介します！

目次（項目クリックでジャンプできます）

この記事の対象者

とにかくフィルタ処理をしたい人

この記事は「理論は後で良い！今はとにかくローパスフィルタやハイパスフィルタをかけなきゃならんのだ！」という人に向けて書いています。

このノイズまみれの信号を今すぐどうにかキレイにしたいけど、プログラミングの学習時間なんてない！

ちょっとcsvデータにフィルタをかけたいだけなのに、社内の高級ソフトをいちいち使うのがダルい…！

…という人、結構いらっしゃると思います。

Pythonワカランな人

本記事ではデジタルフィルタ処理としてローパスフィルタ、ハイパスフィルタ、バンドパスフィルタ、バンドストップフィルタをPythonを使ってかけます。

しかし、Pythonの事を何も知らない人でも最後まで読み進められるように記事を構成してみました。

さらに、会社等でプロキシ設定に阻まれてライブラリインストール出来ない人も対象にしています。インターネットに接続できて、PyPIにアクセスできれば問題ありません。
もちろん全て無料です。

本記事の目標

csvファイルの複数信号を一度にフィルタ処理する

この記事は以下のフォーマットで時間波形が記録されたデータにフィルタをかけます。おそらく色々なデータロガーでcsv出力するとこのような形式になっている事でしょう。

この形式は「ただPythonでcsvから離散フーリエ変換をするだけのコード」と全く同じフォーマットであるため、フィルタをかけたりフーリエ変換したりと時間波形処理を行き来する事が出来ます。

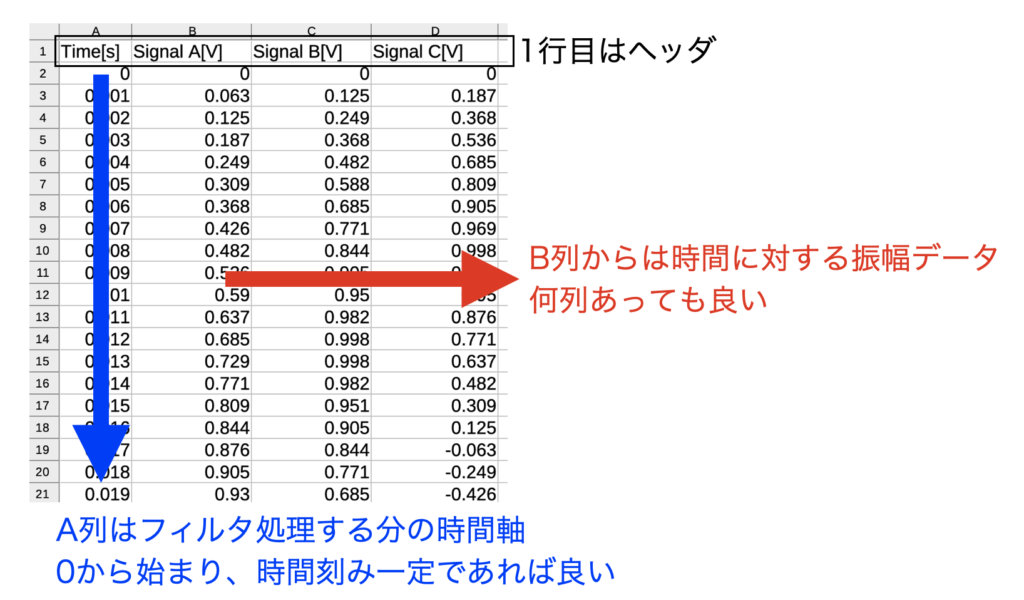
1行目はヘッダです。A列に時間[s]、B列以降は各信号の名称でも書いておきます（わかりやすくするためであって、名前は何でも良いです）。

A列はフィルタ処理する分だけの時間軸を用意しておいて下さい。時間刻みは一定（等ピッチ）である必要があります。但し、フィルタをかける時の周波数が表現できていないとプログラムエラーとなりますので、ご注意下さい。
（例：0.1[s]刻みの粗いデータに1000[Hz]のフィルタをかける…等）

B列以降はA列の各時刻に対応した振幅成分（例えば電圧、加速度…といった物理的な波形）を用意します。ファイルが許す限り列方向に信号を並べておいて構いません。

もっと詳しいフィルタ処理の記事を読みたい人は…

本記事は最速で、この記事だけでフィルタ処理をかける事を目標としていますが、その他過去WATLABブログで書いたフィルタ処理の記事を見たい方は以下のリンクにアクセスしてみて下さい。

検証済の動作環境

PC

僕は以下のWindows環境、Mac環境で本記事のコードを動作検証しています。Linuxやその他OSは対象としていません。

Windows	OS	Windows10 64bit
	CPU	2.4[GHz]
	メモリ	4[GB]

Mac	OS	macOS Catalina 10.15.7
	CPU	1.4[GHz]
	メモリ	8[GB]

Python環境

この後説明するPython環境に関するバージョン情報は以下表に示す通りです。おそらく最新バージョンでも動くと思いますが、検証したのは下の環境のみ。とにかくはやくフィルタ処理したい場合は揃えておくのが無難かと思います。

PythonはPython本体、PyCharmはプログラムを記述して実行したりデバッグしたりする統合開発環境（IDE）、Numpy・Scipy・Pandas・matplotlibはPythonにインポートして使う便利な外部ライブラリです。

Python	Python 3.7.7
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.19.0
Scipy	1.4.1
Pandas	1.0.5
matplotlib	3.2.2

以上の前置きを確認したら、早速環境構築をしていきましょう！環境が既に構築されている人はコード部分までスクロールして下さい。

環境構築

Pythonのインストール

はじめにプログラミング言語であるPythonをインストールしましょう。

PythonのインストールにはAnacondaを推奨する書籍やサイトが沢山ありますが、2021年現在Anacondaは商用利用に制限がかかっているようです。それ以外にも色々面倒な管理となりそうであるため、筆者はAnacondaを使っていません（いちいちライブラリをインストールするのは面倒ですが）。

インストールの方法はWindowsとMacで以下の記事をご確認下さい。

Windows版：「Pythonのインストール方法とAnacondaを使わない3つの理由」

Mac版：「macOSにPython3をインストールする方法をまとめてみた」

そのうちもっと良い環境構築方法も試してみたいと思います（Dockerとか？）

統合開発環境(IDE)のインストール

コードを打ち込んでプログラムを実行するだけならテキストエディタを使ってコマンドプロンプトやターミナルで実行する方法でも十分ですが、デバッグやコード記述補助機能を利用するためには統合開発環境（IDE）を使うのが良いです。

こちらも以下のWindowsとMacで記事を用意していますので、参照しながらインストールしてみて下さい。

Windows版：「Pythonの統合開発環境(IDE)はPyCharmで良い？」

Mac版：「macOSにPython統合開発環境PyCharmをインストール」

外部ライブラリのpipインストール

pip概要と外部ライブラリのインストール方法

先ほど紹介したNumpyやScipyといった外部ライブラリはpipインストールするのが一般的です。

pipについての概要は「Pythonのパッケージ管理ツール pip の使い方とコマンド集」、Windows版とMac版のコマンドの違いは「独断！Pythonでpipインストールしたい外部ライブラリまとめ」をご確認下さい。

プロキシエラーになる場合

もしかするとpipインストール時にプロキシエラーが発生するかも知れません。

PyPIにアクセスできるインターネット環境をお持ちであれば、「pip installでプロキシエラーになる問題を解決する方法」に記載の方法で解決可能です。

※もし社内プロキシ等でひっかかる人は念のためネットワーク管理者にお問い合わせした方が良いかもしれませんが。

csvをフィルタ処理するPythonコード

準備するcsvファイル【ダウンロード可】

ここからはいよいよコードを使ってフィルタ処理をしてみます。
まずはサンプルのcsvファイルとして以下の「signals.csv」をダウンロードしてみて下さい。

サンプルは10[Hz], 20[Hz], 30[Hz]のサイン波が0.001[s]の時間刻みで記録されています。

signals ダウンロード

あとはこのファイルの中身を自分のデータに書き換えて下のコードを実行するだけで目的は達成できるはずです。

ただ、書き換える時はエンコードを「SHIFT-JIS」にする事を忘れずに。もし「UTF-8」で作ってもコードの方を変更すれば大丈夫ですが。

全コード【コピペ・2次利用可】

以下にcsvをフィルタ処理するだけの全コードを示します。このコードを実行するとfilter.csvというファイルが生成されます。

import numpy as np
from scipy import signal
import pandas as pd
import matplotlib.pyplot as plt

#ローパスフィルタ
def lowpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "low")            #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# ハイパスフィルタ
def highpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "high")           #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# バンドパスフィルタ
def bandpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "band")           #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# バンドストップフィルタ
def bandstop(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "bandstop")       #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# csvから列方向に順次フィルタ処理を行い保存する関数
def csv_filter(in_file, out_file, type):
    df = pd.read_csv(in_file, encoding='SHIFT-JIS')                  # ファイル読み込み
    dt = df.T.iloc[0,1]                                              # 時間刻み

    # データフレームを初期化
    df_filter = pd.DataFrame()
    df_filter[df.columns[0]] = df.T.iloc[0]

    # ローパスの設定-----------------------------------------------------------------------------
    fp_lp = 15                                                       # 通過域端周波数[Hz]
    fs_lp = 30                                                       # 阻止域端周波数[Hz]

    # ハイパスの設定-----------------------------------------------------------------------------
    fp_hp = 25                                                       # 通過域端周波数[Hz]
    fs_hp = 10                                                       # 阻止域端周波数[Hz]

    # バンドパスの設定---------------------------------------------------------------------------
    fp_bp = np.array([15, 25])                                       # 通過域端周波数[Hz]※ベクトル
    fs_bp = np.array([5, 50])                                        # 阻止域端周波数[Hz]※ベクトル

    # バンドストップの設定---------------------------------------------------------------------------
    fp_bs = np.array([15, 25])                                       # 通過域端周波数[Hz]※ベクトル
    fs_bs = np.array([5, 50])                                        # 阻止域端周波数[Hz]※ベクトル

    gpass = 3                                                        # 通過域端最大損失[dB]
    gstop = 40                                                       # 阻止域端最小損失[dB]

    # 列方向に順次フィルタ処理をするコード
    for i in range(len(df.T)-1):
        data = df.T.iloc[i+1]                       # フィルタ処理するデータ列を抽出

        # フィルタ処理の種類を文字列で読み取って適切な関数を選択する
        if type == 'lp':
            # ローパスフィルタを実行
            print('wave=', i, ':Lowpass.')
            data = lowpass(x=data, samplerate=1 / dt,
                           fp=fp_lp, fs=fs_lp,
                           gpass=gpass, gstop=gstop)
        elif type == 'hp':
            # ハイパスフィルタを実行
            print('wave=', i, ':Highpass.')
            data = highpass(x=data, samplerate=1 / dt,
                           fp=fp_hp, fs=fs_hp,
                           gpass=gpass, gstop=gstop)
        elif type == 'bp':
            # バンドパスフィルタを実行
            print('wave=', i, ':Bandpass.')
            data = bandpass(x=data, samplerate=1/dt,
                            fp=fp_bp, fs=fs_bp,
                            gpass=gpass, gstop=gstop)
        elif type == 'bs':
            # バンドストップフィルタを実行
            print('wave=', i, ':Bandstop.')
            data = bandstop(x=data, samplerate=1/dt,
                            fp=fp_bs, fs=fs_bs,
                            gpass=gpass, gstop=gstop)
        else:
            # 文字列が当てはまらない時はパス（動作テストでフィルタかけたくない時はNoneとか書いて実行するとよい）
            pass

        data = pd.Series(data)                                       # dataをPandasシリーズデータへ変換
        df_filter[df.columns[i + 1] + '_filter'] = data              # 保存用にデータフレームへdataを追加

    df_filter.to_csv(out_file)                                       # フィルタ処理の結果をcsvに保存

    return df, df_filter

# 関数を実行してcsvファイルをフィルタ処理するだけの関数を実行
# type='lp', 'hp', 'bp', 'bs':LowPass, HighPass, BandPass, BandStop
df, df_filter = csv_filter(in_file='signals.csv', out_file='filter.csv', type='lp')

# ここからグラフ描画-------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure(figsize=(10, 7))
ax1 = fig.add_subplot(211)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')
ax2 = fig.add_subplot(212)
ax2.yaxis.set_ticks_position('both')
ax2.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Amplitude_Original')
ax2.set_xlabel('Time [s]')
ax2.set_ylabel('Amplitude_Filtered')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
size = len(df.T)-1
for i in range(size):
    ax1.plot(df.T.iloc[0], df.T.iloc[i+1], label=df.columns[i+1], lw=1)
    ax2.plot(df_filter.T.iloc[0], df_filter.T.iloc[i + 1], label=df_filter.columns[i + 1], lw=1)
ax1.legend()
ax2.legend()

# レイアウト設定
fig.tight_layout()

# グラフを表示する。
plt.show()
plt.close()
# ---------------------------------------------------

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

import numpy as np

from scipy import signal

import pandas as pd

import matplotlib.pyplot as plt

#ローパスフィルタ

def lowpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "low") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# ハイパスフィルタ

def highpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "high") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# バンドパスフィルタ

def bandpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "band") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# バンドストップフィルタ

def bandstop(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "bandstop") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# csvから列方向に順次フィルタ処理を行い保存する関数

def csv_filter(in_file, out_file, type):

df = pd.read_csv(in_file, encoding='SHIFT-JIS') # ファイル読み込み

dt = df.T.iloc[0,1] # 時間刻み

# データフレームを初期化

df_filter = pd.DataFrame()

df_filter[df.columns[0]] = df.T.iloc[0]

# ローパスの設定-----------------------------------------------------------------------------

fp_lp = 15 # 通過域端周波数[Hz]

fs_lp = 30 # 阻止域端周波数[Hz]

# ハイパスの設定-----------------------------------------------------------------------------

fp_hp = 25 # 通過域端周波数[Hz]

fs_hp = 10 # 阻止域端周波数[Hz]

# バンドパスの設定---------------------------------------------------------------------------

fp_bp = np.array([15, 25]) # 通過域端周波数[Hz]※ベクトル

fs_bp = np.array([5, 50]) # 阻止域端周波数[Hz]※ベクトル

# バンドストップの設定---------------------------------------------------------------------------

fp_bs = np.array([15, 25]) # 通過域端周波数[Hz]※ベクトル

fs_bs = np.array([5, 50]) # 阻止域端周波数[Hz]※ベクトル

gpass = 3 # 通過域端最大損失[dB]

gstop = 40 # 阻止域端最小損失[dB]

# 列方向に順次フィルタ処理をするコード

for i in range(len(df.T)-1):

data = df.T.iloc[i+1] # フィルタ処理するデータ列を抽出

# フィルタ処理の種類を文字列で読み取って適切な関数を選択する

if type == 'lp':

# ローパスフィルタを実行

print('wave=', i, ':Lowpass.')

data = lowpass(x=data, samplerate=1 / dt,

fp=fp_lp, fs=fs_lp,

gpass=gpass, gstop=gstop)

elif type == 'hp':

# ハイパスフィルタを実行

print('wave=', i, ':Highpass.')

data = highpass(x=data, samplerate=1 / dt,

fp=fp_hp, fs=fs_hp,

gpass=gpass, gstop=gstop)

elif type == 'bp':

# バンドパスフィルタを実行

print('wave=', i, ':Bandpass.')

data = bandpass(x=data, samplerate=1/dt,

fp=fp_bp, fs=fs_bp,

gpass=gpass, gstop=gstop)

elif type == 'bs':

# バンドストップフィルタを実行

print('wave=', i, ':Bandstop.')

data = bandstop(x=data, samplerate=1/dt,

fp=fp_bs, fs=fs_bs,

gpass=gpass, gstop=gstop)

else:

# 文字列が当てはまらない時はパス（動作テストでフィルタかけたくない時はNoneとか書いて実行するとよい）

pass

data = pd.Series(data) # dataをPandasシリーズデータへ変換

df_filter[df.columns[i + 1] + '_filter'] = data # 保存用にデータフレームへdataを追加

df_filter.to_csv(out_file) # フィルタ処理の結果をcsvに保存

return df, df_filter

# 関数を実行してcsvファイルをフィルタ処理するだけの関数を実行

# type='lp', 'hp', 'bp', 'bs':LowPass, HighPass, BandPass, BandStop

df, df_filter = csv_filter(in_file='signals.csv', out_file='filter.csv', type='lp')

# ここからグラフ描画-------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure(figsize=(10, 7))

ax1 = fig.add_subplot(211)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = fig.add_subplot(212)

ax2.yaxis.set_ticks_position('both')

ax2.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('Amplitude_Original')

ax2.set_xlabel('Time [s]')

ax2.set_ylabel('Amplitude_Filtered')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

size = len(df.T)-1

for i in range(size):

ax1.plot(df.T.iloc[0], df.T.iloc[i+1], label=df.columns[i+1], lw=1)

ax2.plot(df_filter.T.iloc[0], df_filter.T.iloc[i + 1], label=df_filter.columns[i + 1], lw=1)

ax1.legend()

ax2.legend()

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

# ---------------------------------------------------

実行結果

フィルタ後のcsvファイル

生成されたcsvファイルの例を以下に示します。今回はB列に時間（signal.csvのコピー）、以降は対応する振幅のデータが最初に指定したデータ数分順番に並びます。

フィルタ前後の時間波形比較

グラフの例は下図です。パッと確認したい時はPython上で見るのが一番ですね。

サンプルのプログラムはcsv_filter関数実行時にtype='lp'とローパスフィルタを指定しています。

また、関数内で通過域端周波数fp_lp=15[Hz]、阻止域端周波数fs_lp=30[Hz]を設定しているため、10[Hz]のサイン波はあまりフィルタの影響を受けませんが、20[Hz]と30[Hz]のサイン波は振幅が大きく減少している結果を得る事を出来ます。

※上段がフィルタ前、下段がフィルタ後です。

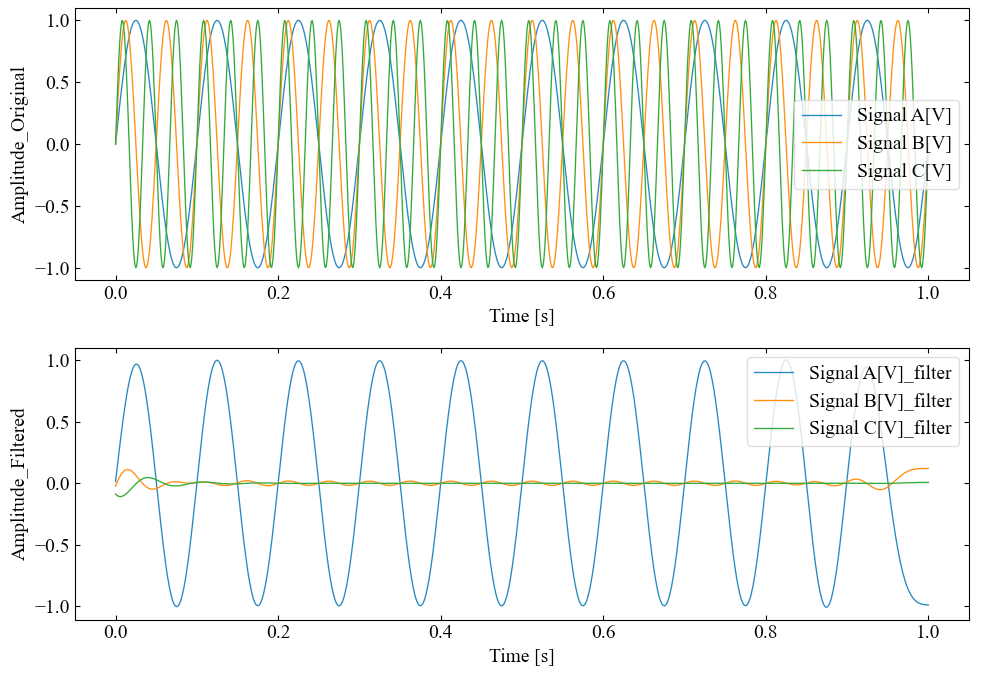
以上でcsvファイルに記録した時間波形へフィルタ処理をかける事ができました。

しかし、csvに記録されたフィルタ後の波形を周波数軸で確認するためには、出来上がったフィルタ後のcsvファイルに対し、フーリエ変換のコードを適用させる必要があります。

…ここまでやったんだから、ねぇ？

フーリエ変換とプロット確認コードも付けますかね！

csvをフィルタ処理するPythonコード(フーリエ変換機能付き)

フィルタ処理は一度設定が確定するまで、フーリエ変換で所望の結果が得られるかどうかを確認する事をよくやります。

ここではフィルタの設定をその場で確かめるためのフーリエ変換機能を追加したコードを紹介します。

…と言っても「ただPythonでcsvから離散フーリエ変換をするだけのコード」の内容と組み合わせただけで特に新しい事は何もありません！

全コード【コピペ・2次利用可】

先ほどのコードに比べ、importでfftpackをインポートしている点、「# フーリエ変換確認用------」と書いてある部分2箇所と、プロット部分を変更しています。

import numpy as np
from scipy import fftpack
from scipy import signal
import pandas as pd
import matplotlib.pyplot as plt

# フーリエ変換をする関数
def calc_fft(data, samplerate):
    spectrum = fftpack.fft(data)                                     # 信号のフーリエ変換
    amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2))       # 振幅成分
    amp = amp / (len(data) / 2)                                      # 振幅成分の正規化（辻褄合わせ）
    phase = np.arctan2(spectrum.imag, spectrum.real)                 # 位相を計算
    phase = np.degrees(phase)                                        # 位相をラジアンから度に変換
    freq = np.linspace(0, samplerate, len(data))                     # 周波数軸を作成
    return spectrum, amp, phase, freq

#ローパスフィルタ
def lowpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "low")            #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# ハイパスフィルタ
def highpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "high")           #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# バンドパスフィルタ
def bandpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "band")           #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# バンドストップフィルタ
def bandstop(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "bandstop")       #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y

# csvから列方向に順次フィルタ処理を行い保存する関数
def csv_filter(in_file, out_file, type):
    df = pd.read_csv(in_file, encoding='SHIFT-JIS')                  # ファイル読み込み
    dt = df.T.iloc[0,1]                                              # 時間刻み

    # データフレームを初期化
    df_filter = pd.DataFrame()
    df_filter[df.columns[0]] = df.T.iloc[0]

    # フーリエ変換確認用---------------------------------------------------------------------------------------
    df_amp = pd.DataFrame()
    df_phase = pd.DataFrame()
    df_fft = pd.DataFrame()
    # ------------------------------------------------------------------------------------------------------

    # ローパスの設定-----------------------------------------------------------------------------
    fp_lp = 15                                                       # 通過域端周波数[Hz]
    fs_lp = 30                                                       # 阻止域端周波数[Hz]

    # ハイパスの設定-----------------------------------------------------------------------------
    fp_hp = 25                                                       # 通過域端周波数[Hz]
    fs_hp = 10                                                       # 阻止域端周波数[Hz]

    # バンドパスの設定---------------------------------------------------------------------------
    fp_bp = np.array([15, 25])                                       # 通過域端周波数[Hz]※ベクトル
    fs_bp = np.array([5, 50])                                        # 阻止域端周波数[Hz]※ベクトル

    # バンドストップの設定---------------------------------------------------------------------------
    fp_bs = np.array([15, 25])                                       # 通過域端周波数[Hz]※ベクトル
    fs_bs = np.array([5, 50])                                        # 阻止域端周波数[Hz]※ベクトル

    gpass = 3                                                        # 通過域端最大損失[dB]
    gstop = 40                                                       # 阻止域端最小損失[dB]

    # 列方向に順次フィルタ処理をするコード
    for i in range(len(df.T)-1):
        data = df.T.iloc[i+1]                       # フィルタ処理するデータ列を抽出

        # フィルタ処理の種類を文字列で読み取って適切な関数を選択する
        if type == 'lp':
            # ローパスフィルタを実行
            print('wave=', i, ':Lowpass.')
            data = lowpass(x=data, samplerate=1 / dt,
                           fp=fp_lp, fs=fs_lp,
                           gpass=gpass, gstop=gstop)
        elif type == 'hp':
            # ハイパスフィルタを実行
            print('wave=', i, ':Highpass.')
            data = highpass(x=data, samplerate=1 / dt,
                           fp=fp_hp, fs=fs_hp,
                           gpass=gpass, gstop=gstop)
        elif type == 'bp':
            # バンドパスフィルタを実行
            print('wave=', i, ':Bandpass.')
            data = bandpass(x=data, samplerate=1/dt,
                            fp=fp_bp, fs=fs_bp,
                            gpass=gpass, gstop=gstop)
        elif type == 'bs':
            # バンドストップフィルタを実行
            print('wave=', i, ':Bandstop.')
            data = bandstop(x=data, samplerate=1/dt,
                            fp=fp_bs, fs=fs_bs,
                            gpass=gpass, gstop=gstop)
        else:
            # 文字列が当てはまらない時はパス（動作テストでフィルタかけたくない時はNoneとか書いて実行するとよい）
            pass

        data = pd.Series(data)                                       # dataをPandasシリーズデータへ変換
        df_filter[df.columns[i + 1] + '_filter'] = data              # 保存用にデータフレームへdataを追加

    # フーリエ変換確認用---------------------------------------------------------------------------------------
        spectrum, amp, phase, freq = calc_fft(data.values, 1/dt)     # フーリエ変換をする関数を実行
        df_amp[df.columns[i+1] + '_amp'] = pd.Series(amp)            # 列名と共にデータフレームに振幅計算結果を追加
        df_phase[df.columns[i+1] + '_phase[deg]'] = pd.Series(phase) # 列名と共にデータフレームに位相計算結果を追加

    df_fft['freq[Hz]'] = pd.Series(freq)                             # 周波数軸を作成
    df_fft = df_fft.join(df_amp).join(df_phase)                      # 周波数・振幅・位相のデータフレームを結合
    df_fft = df_fft.iloc[range(int(len(df)/2)),:]                    # ナイキスト周波数でデータを切り捨て
    # ------------------------------------------------------------------------------------------------------

    df_filter.to_csv(out_file)                                       # フィルタ処理の結果をcsvに保存

    return df, df_filter, df_fft

# 関数を実行してcsvファイルをフィルタ処理するだけの関数を実行
# type='lp', 'hp', 'bp', 'bs':LowPass, HighPass, BandPass, BandStop
df, df_filter, df_fft = csv_filter(in_file='signals.csv', out_file='filter.csv', type='lp')

# ここからグラフ描画-------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure(figsize=(10, 7))
ax1 = fig.add_subplot(221)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')
ax2 = fig.add_subplot(223)
ax2.yaxis.set_ticks_position('both')
ax2.xaxis.set_ticks_position('both')
ax3 = fig.add_subplot(122)
ax3.yaxis.set_ticks_position('both')
ax3.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Amplitude_Original')
ax2.set_xlabel('Time [s]')
ax2.set_ylabel('Amplitude_Filtered')
ax3.set_xlabel('Frequency [Hz]')
ax3.set_ylabel('Amplitude_Filtered')

# スケールの設定をする。
ax3.set_yscale('log')
ax3.set_xscale('log')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
size = len(df.T)-1
for i in range(size):
    ax1.plot(df.T.iloc[0], df.T.iloc[i+1], label=df.columns[i+1], lw=1)
    ax2.plot(df_filter.T.iloc[0], df_filter.T.iloc[i + 1], label=df_filter.columns[i + 1], lw=1)
    ax3.plot(df_fft.T.iloc[0], df_fft.T.iloc[i+1], label=df_fft.columns[i+1], lw=1)
ax1.legend()
ax2.legend()
ax3.legend()

# レイアウト設定
fig.tight_layout()

# グラフを表示する。
plt.show()
plt.close()
# ---------------------------------------------------

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

import numpy as np

from scipy import fftpack

from scipy import signal

import pandas as pd

import matplotlib.pyplot as plt

# フーリエ変換をする関数

def calc_fft(data, samplerate):

spectrum = fftpack.fft(data) # 信号のフーリエ変換

amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分

amp = amp / (len(data) / 2) # 振幅成分の正規化（辻褄合わせ）

phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算

phase = np.degrees(phase) # 位相をラジアンから度に変換

freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成

return spectrum, amp, phase, freq

#ローパスフィルタ

def lowpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "low") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# ハイパスフィルタ

def highpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "high") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# バンドパスフィルタ

def bandpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "band") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# バンドストップフィルタ

def bandstop(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "bandstop") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y

# csvから列方向に順次フィルタ処理を行い保存する関数

def csv_filter(in_file, out_file, type):

df = pd.read_csv(in_file, encoding='SHIFT-JIS') # ファイル読み込み

dt = df.T.iloc[0,1] # 時間刻み

# データフレームを初期化

df_filter = pd.DataFrame()

df_filter[df.columns[0]] = df.T.iloc[0]

# フーリエ変換確認用---------------------------------------------------------------------------------------

df_amp = pd.DataFrame()

df_phase = pd.DataFrame()

df_fft = pd.DataFrame()

# ------------------------------------------------------------------------------------------------------

# ローパスの設定-----------------------------------------------------------------------------

fp_lp = 15 # 通過域端周波数[Hz]

fs_lp = 30 # 阻止域端周波数[Hz]

# ハイパスの設定-----------------------------------------------------------------------------

fp_hp = 25 # 通過域端周波数[Hz]

fs_hp = 10 # 阻止域端周波数[Hz]

# バンドパスの設定---------------------------------------------------------------------------

fp_bp = np.array([15, 25]) # 通過域端周波数[Hz]※ベクトル

fs_bp = np.array([5, 50]) # 阻止域端周波数[Hz]※ベクトル

# バンドストップの設定---------------------------------------------------------------------------

fp_bs = np.array([15, 25]) # 通過域端周波数[Hz]※ベクトル

fs_bs = np.array([5, 50]) # 阻止域端周波数[Hz]※ベクトル

gpass = 3 # 通過域端最大損失[dB]

gstop = 40 # 阻止域端最小損失[dB]

# 列方向に順次フィルタ処理をするコード

for i in range(len(df.T)-1):

data = df.T.iloc[i+1] # フィルタ処理するデータ列を抽出

# フィルタ処理の種類を文字列で読み取って適切な関数を選択する

if type == 'lp':

# ローパスフィルタを実行

print('wave=', i, ':Lowpass.')

data = lowpass(x=data, samplerate=1 / dt,

fp=fp_lp, fs=fs_lp,

gpass=gpass, gstop=gstop)

elif type == 'hp':

# ハイパスフィルタを実行

print('wave=', i, ':Highpass.')

data = highpass(x=data, samplerate=1 / dt,

fp=fp_hp, fs=fs_hp,

gpass=gpass, gstop=gstop)

elif type == 'bp':

# バンドパスフィルタを実行

print('wave=', i, ':Bandpass.')

data = bandpass(x=data, samplerate=1/dt,

fp=fp_bp, fs=fs_bp,

gpass=gpass, gstop=gstop)

elif type == 'bs':

# バンドストップフィルタを実行

print('wave=', i, ':Bandstop.')

data = bandstop(x=data, samplerate=1/dt,

fp=fp_bs, fs=fs_bs,

gpass=gpass, gstop=gstop)

else:

# 文字列が当てはまらない時はパス（動作テストでフィルタかけたくない時はNoneとか書いて実行するとよい）

pass

data = pd.Series(data) # dataをPandasシリーズデータへ変換

df_filter[df.columns[i + 1] + '_filter'] = data # 保存用にデータフレームへdataを追加

# フーリエ変換確認用---------------------------------------------------------------------------------------

spectrum, amp, phase, freq = calc_fft(data.values, 1/dt) # フーリエ変換をする関数を実行

df_amp[df.columns[i+1] + '_amp'] = pd.Series(amp) # 列名と共にデータフレームに振幅計算結果を追加

df_phase[df.columns[i+1] + '_phase[deg]'] = pd.Series(phase) # 列名と共にデータフレームに位相計算結果を追加

df_fft['freq[Hz]'] = pd.Series(freq) # 周波数軸を作成

df_fft = df_fft.join(df_amp).join(df_phase) # 周波数・振幅・位相のデータフレームを結合

df_fft = df_fft.iloc[range(int(len(df)/2)),:] # ナイキスト周波数でデータを切り捨て

# ------------------------------------------------------------------------------------------------------

df_filter.to_csv(out_file) # フィルタ処理の結果をcsvに保存

return df, df_filter, df_fft

# 関数を実行してcsvファイルをフィルタ処理するだけの関数を実行

# type='lp', 'hp', 'bp', 'bs':LowPass, HighPass, BandPass, BandStop

df, df_filter, df_fft = csv_filter(in_file='signals.csv', out_file='filter.csv', type='lp')

# ここからグラフ描画-------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure(figsize=(10, 7))

ax1 = fig.add_subplot(221)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = fig.add_subplot(223)

ax2.yaxis.set_ticks_position('both')

ax2.xaxis.set_ticks_position('both')

ax3 = fig.add_subplot(122)

ax3.yaxis.set_ticks_position('both')

ax3.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('Amplitude_Original')

ax2.set_xlabel('Time [s]')

ax2.set_ylabel('Amplitude_Filtered')

ax3.set_xlabel('Frequency [Hz]')

ax3.set_ylabel('Amplitude_Filtered')

# スケールの設定をする。

ax3.set_yscale('log')

ax3.set_xscale('log')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

size = len(df.T)-1

for i in range(size):

ax1.plot(df.T.iloc[0], df.T.iloc[i+1], label=df.columns[i+1], lw=1)

ax2.plot(df_filter.T.iloc[0], df_filter.T.iloc[i + 1], label=df_filter.columns[i + 1], lw=1)

ax3.plot(df_fft.T.iloc[0], df_fft.T.iloc[i+1], label=df_fft.columns[i+1], lw=1)

ax1.legend()

ax2.legend()

ax3.legend()

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

# ---------------------------------------------------

実行結果

ローパスフィルタ後の周波数波形確認

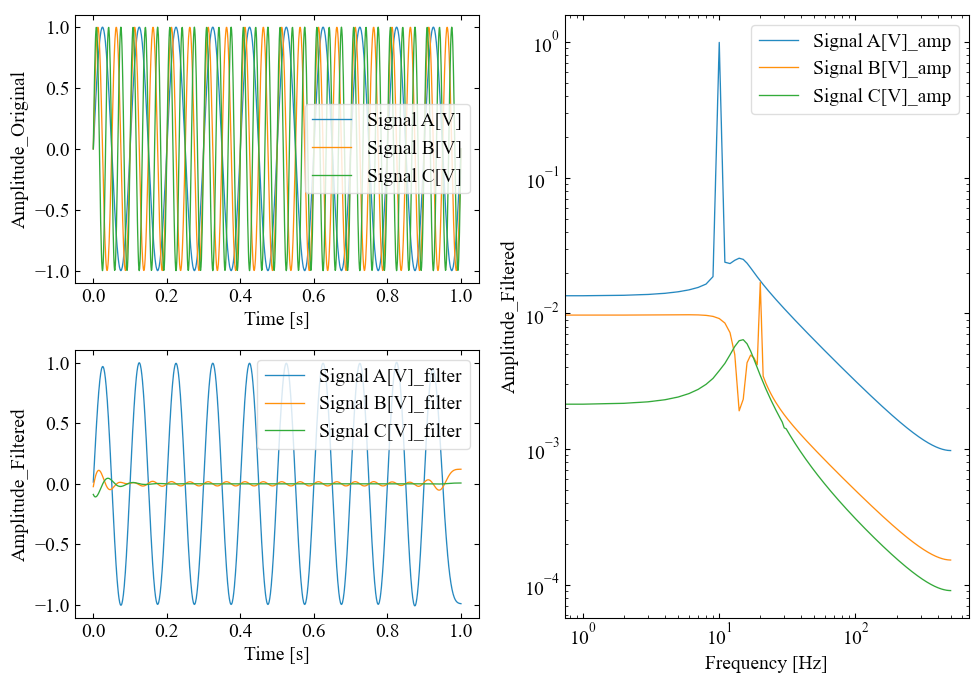
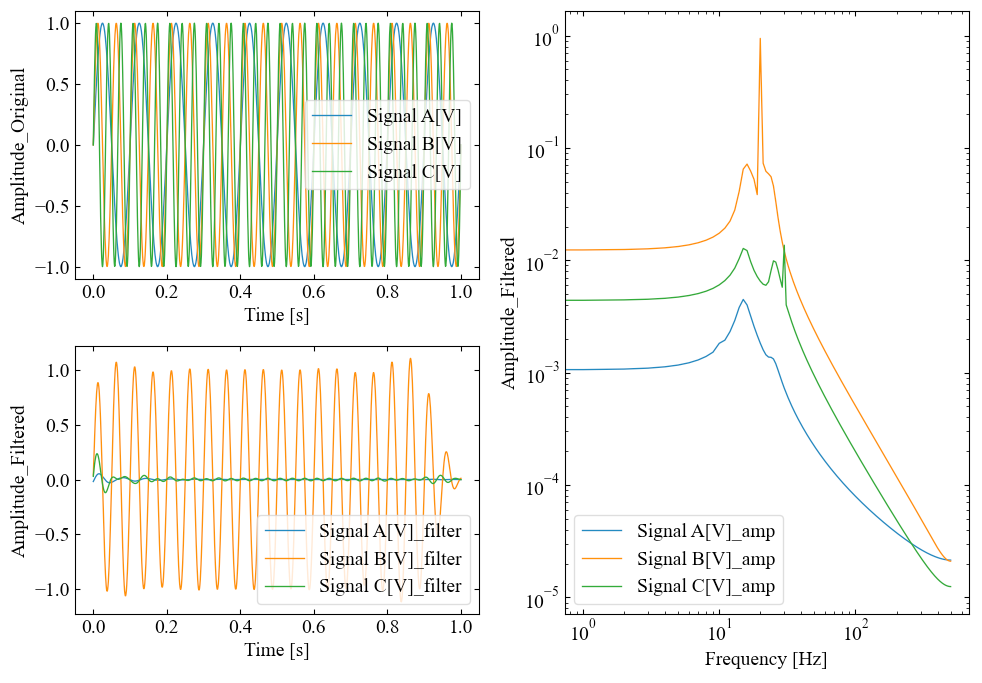
以下はtype='lp'で関数実行した結果です。

右側のブロックにフーリエ変換した波形をプロットしていますが、10[Hz]のピークはほぼ原型を留めているのに対し、その他の次数は振幅低減している事が周波数波形からも確かめられました。想定通りです。

ハイパスフィルタ後の周波数波形確認

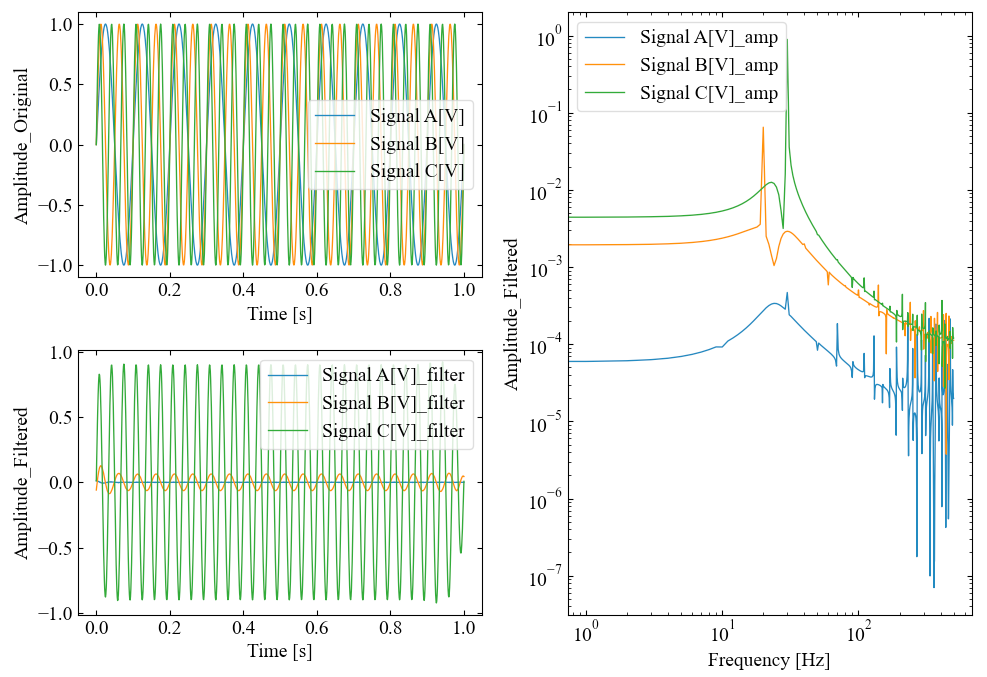
以下はtype='hp'で関数実行した結果です。

今度は高周波側である30[Hz]の次数を残し、その他の次数を低減させました。想定通りですね。

バンドパスフィルタ後の周波数波形確認

以下はtype='bp'で関数実行した結果です。

バンドパスの場合はデフォルトで20[Hz]が残るようにしてあります。想定通り。

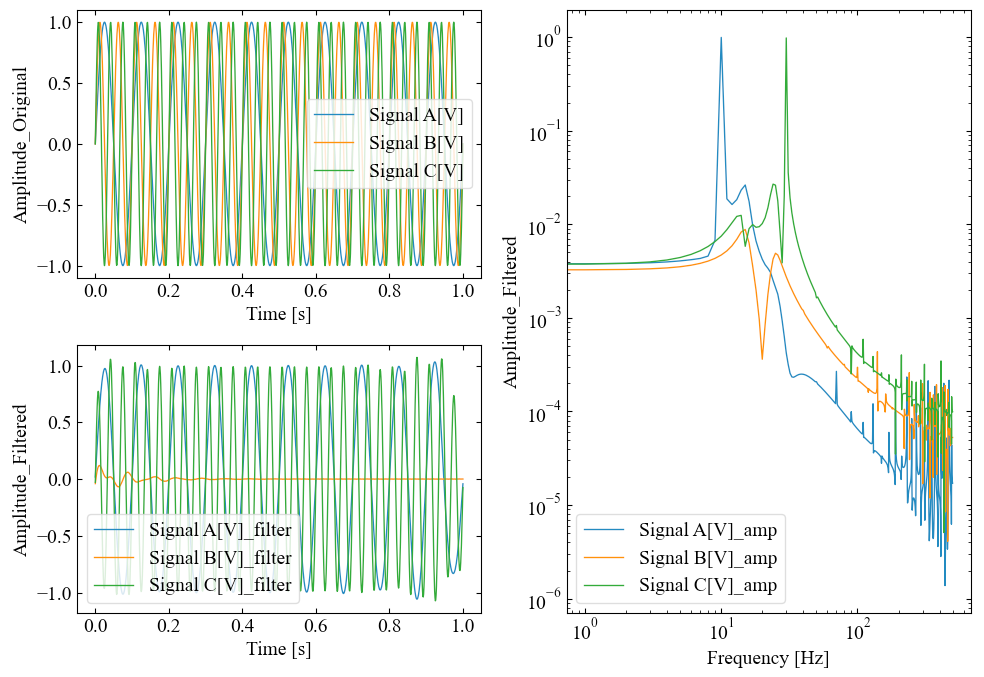
バンドストップフィルタ後の周波数波形確認

以下はtype='bs'で関数実行した結果です。

バンドストップは逆に20[Hz]のみを低減する設定にしています。これも想定通り。

以上でcsvファイルにフィルタをかけるPythonコードの紹介は終了です。関数内の周波数設定を色々と変更して遊んでみて下さい！

まとめ

本ページでは検索から初めて当ブログに辿り付いた「Pythonはよくワカランけど、とにかく最速でフィルタ処理をしたい人」を対象に目標設定、Python環境の導入から説明しました。

csvファイルもサンプルをダウンロード可能としたため、環境さえ整えばすぐにフィルタ処理を試す事ができると思います。

ただ、現在のコードは周波数設定部分がcsv_filter関数の中にあるので、もしかしたらさらなる改善として関数の外から設定するようにした方が良いかも知れません（やってみて下さい！）。

また、実用性を考えフーリエ変換コードと組み合わせたコードも紹介しました。
是非自身のデータに対して色々なフィルタをかける信号処理ライフをお楽しみ下さい！

wat

機械工学を専攻し大学院を修了後、技術系の職に就き日々実験やシミュレーションを使う仕事をしています。このブログでは初心者が科学技術プログラムを作れるようになることを目標に、学習結果を記録していきます。著書「いきなりプログラミングPython（翔泳社）」 ※資格・計算力学技術者 1級 2級 (振動) ・計算力学技術者 2級 (熱流体) ・基本情報技術者・G検定・AI実装検定 S級 A級 ※Information ・Amazonのアソシエイトとして、当メディアは適格販売により収入を得ています。・当メディアはGoogleによるユーザーに合わせた自動広告が表示されます。

hiroko より:

2021年8月17日 5:45 PM

読みやすいブログでいつも楽しみにしています。
掲載されていたサンプルデータで試してみると、上手くいきました。ありがとうございます。
気になったのですが、”dt”はプログラムで読み取られる設定ですが、以下のデータを使う時には”256″に置き替えた方がよいのでしょうか。

CSVは以下のように記載しています。
A列は0, 0.0.00390625, 0.0078125, ・・・, 511.9960938
B列以降の各列の情報
　サンプリング数　：131,072
　サンプリング周期：1/256秒

返信
1. hiroko より:
  
  2021年8月17日 6:16 PM
  
  “dt”に256を入れるとエラーになってしまいました。
  なので、そのままでよかったですね。すみません。。。色々試してみたら混乱してました。
  
  返信
  1. wat より:
    
    2021年8月18日 11:56 PM
    
    いつもご利用ありがとうございます。
    返信遅れました！
    dtはdelta t(time)の略でよく信号処理で使う「時間刻み」、あるいは「時間分解能」と呼ばれるものです。
    データの時間刻みなので0[s], 0.1[s], 0.2[s]…とデータが記録されている場合はdt=0.1[s]です。
    hirokoさんの場合ですと、dt=0.00390625[s]でしょうか。
    プログラムでは自動で読み取っていますが、print(dt)等でご確認頂けるとわかりやすいかも知れません。
    以上、よろしくお願い致します。
    
    返信
まるより:

2021年11月22日 4:40 PM

初めまして
私は最近、Pythonを使い始めたものです。
仕事でFFT処理をする機会があり検索していたところこちらのページが見つかり参考にさせていただいております。
その中で質問がありコメントさせていただきました。

とりあえずコピペして動かしたのですが、csvfileの場所が見当たりませんというエラーが出ており、おそらく構文中のどこかでファイルなパスを指定すると思うのですが

# csvから列方向に順次フィルタ処理を行い保存する関数
def csv_filter(in_file, out_file, type):
df = pd.read_csv(in_file, encoding=’SHIFT-JIS’)
というコードがあると思うのですが、
この文中のin_fileを変更すれば良いのでしょうか？とても初歩的なことだと思いますがもしよろしければご回答よろしくお願いいたします。

返信
1. wat より:
  
  2021年11月22日 11:16 PM
  
  ご訪問ありがとうございます。
  def csv_filter(in_file, …):のin_fileは間数の引数に設定してあるので変更はしない方が良いです。
  
  関数を実行してcsvファイルをフィルタ処理するだけの関数を実行
  # type=’lp’, ‘hp’, ‘bp’, ‘bs’:LowPass, HighPass, BandPass, BandStop
  df, df_filter = csv_filter(in_file=’signals.csv’, out_file=’filter.csv’, type=’lp’)
  →の「in_file=”」にここに指定のファイルパスを記入すると読み込まれるはずです。
  
  もしくはPythonプログラム実行フォルダに「signals.csv」名前でファイルを置く事でも読み込まれるはずですので、ご確認下さい。
  
  よろしくお願い致します。
  
  返信
  1. まるより:
    
    2021年11月23日 10:20 AM
    
    いつもお世話になっております。
    返信いただいた部分を修正したところ無事にフィルタリング処理ができました。大変助かりました。
    
    処理後新たな疑問が生まれたのですが、処理後のCSVファイル(filtercsv)が生成されるとありますがこちらはどこに生成されるのでしょうか？構文中にまた生成場所をしていすれば良いでしょうか？
    
    返信
まるより:

2021年11月23日 1:13 PM

すみません、調べたところしっかり
filter csvが生成できていました！
ありがとうございました！

返信
1. wat より:
  
  2021年11月23日 9:42 PM
  
  自己解決されたようで何よりです！
  わざわざご連絡ありがとうございます。
  今後も是非Pythonをお楽しみ下さい。
  
  返信
よーだより:

2022年4月8日 1:34 AM

最近pytohnを使い始めました。
筋電データにバンドパスをかけるためにこの記事を見て勉強させていただきました。
大変参考になり、ありがとうございます。
一点理解できなかった部分があるのですが、下記のコードの意味をご教示いただけないでしょうか。
「dt = df.T.iloc[0,1] # 時間刻み」
例えば0,1の数値を0,2や1,1に変更すると、処理にどのような変化が出てくるのか、教えていただけるとありがたいです。

返信
1. wat より:
  
  2022年4月8日 9:49 PM
  
  ご訪問ありがとうございます。
  dtは時間刻みを意味しており、今回のcsvを使うコードでは[0,1]に時間刻み値を入力する仕様になっています。
  0列が時間軸を書く場所になっており、最初にヘッダを削除しているので、
  時間軸が[0, 0.1, 0.2, 0.3….]と入っている時は0.1[s]が抽出されます。
  
  時間刻み情報からサンプリング周波数を計算していますので、この値を間違うとフィルタの周波数設定が意図したものになりません。
  例えば[0,2]にすると倍の時間刻みになってしいますし、[1,1]にしてしまうとそもそも時間軸ではなく、データ軸から値を取得するためフィルタリング以前の問題です。
  
  実際に値を変更してフーリエ変換後の波形をご覧頂ければ、おそらくフィルタのかかり方が大きく変わることを確認できると思います。
  
  以上、よろしくお願い致します。
  
  返信
  1. よーだより:
    
    2022年4月9日 1:34 AM
    
    初心者的なご質問にもかかわらずご丁寧にご返信くださりありがとうございます。
    理解することができました。
    サンプリング周波数自体は手入力ではなく自動抽出だったのですね。。。
    ありがとうございました！
    
    返信
    1. wat より:
      
      2022年4月9日 9:32 AM
      
      解決したようで安心しました。
      また不明点がございましたらお気軽にコメントください。
      よろしくお願いいたします。
      
      返信
よーだより:

2022年4月25日 10:09 AM

お世話になります。
先日はご質問にご回答いただきありがとうございました。

重ねての質問となり恐縮なのですが、フィルタ後のcsvファイルのA列には、データのIDが付与されているかと思うのですが、A列のIDデータを出力しない方法はございますでしょうか。

本サイトの実行結果部に記載いただいております、B,C,D, E列データを、A, B, C, D列に出力し、A列データは出力しないというようなイメージになります。

返信
1. wat より:
  
  2022年4月26日 9:54 PM
  
  A列のIDデータを出力しないようにするためには、
  　　　　df_filter.to_csv(out_file, index=False) # フィルタ処理の結果をcsvに保存
  のように、.to_csvの引数indexにFalseを指定することで実現可能です。
  是非お試しください。
  
  返信
  1. よーだより:
    
    2022年4月27日 12:13 AM
    
    ご丁寧にご教示いただきありがとうございました！
    うまくいきました！
    
    返信
shin より:

2022年5月10日 5:20 PM

いつも参考にさせていただき、大変勉強になります。
プログラム紹介のページという趣旨とは異なりますし、まだまだ勉強中の身でプログラムの中身も正しく理解できていないかもしれませんが、質問させて下さい。

今回のプログラムではサンプリングしたであろう生データ（CSVファイル）に対して、フィルタ処理を行い、その結果に対してFFTをかけているように思いますが、
これはFFTをかけたのちに必要とする周波数範囲以外に0の値を代入し、逆FFTをかけるのとは違ったものになるのでしょうか？
（例えばbpであれば15～25Hz以外の値に0を代入したのちに逆FFTをおこなう）

FFTで周波数ごとに信号を分離できているので、その値を利用するほうが、フィルタの勾配を気にする必要が無く0、100で完全分離できるより高精度なフィルタとして機能するように感じますし、それがデジタル処理しているメリットなのかなと思ったのですが、
それをやらないということは、そもそもこの考えが間違っているのでしょうか？可能でしたらご教示いただければ幸いです。

返信
1. wat より:
  
  2022年5月11日 10:48 PM
  
  ご訪問ありがとうございます。
  こちらも勉強中の身であり、信号処理に関しても独学のため間違ったことを言うかも知れませんが、個人的な解釈を以下に書こうと思います。
  （ここにコメント残しておけば誰か専門家が答えてくれるかも。。。と期待）
  
  ・時間変動しない定常信号ならFFTのフィルタでも良いと思います。
  shinさんが仰るようにFFTとIFFTによるフィルタリングも可能で、フィルタ勾配を最も急峻にできると思います。
  しかし、計測器で信号を取得しフーリエ変換するには、ある一定時間分の信号で平均化する必要があります。
  理想的な正弦波のような信号に対してはそれで良いですが、時間波形が常に変動（振幅や周波数がごく短い時間で変化する）場合には向きません。
  
  この記事で紹介しているフィルタはライブラリを使っているだけですが、時間波形に対するディジタルフィルタは「移動平均」の応用版です。
  ローパスやハイパスは移動平均時のデータ点数やデータ点に対する重み付けを行うことで周波数特性を設計でき、変動する時間波形に対しても設定した周波数特性を持たせることができるようです（この辺説明はだいぶ正確さを欠いていると思うのでご注意ください）。
  
  そのうちもう少し勉強して記事書きたいです(^^;
  
  返信
  1. shin より:
    
    2022年5月23日 12:51 PM
    
    丁寧に説明していただきありがとうございます。
    確かに平均化している以上、正しくフィルターとしては機能しなさそうですね
    まだまだ勉強中なので、全部は理解できていないですが、今後の記事も楽しみにしております。
    
    返信
CCC より:

2022年9月7日 5:50 PM

お世話になります。
非常にわかりやすい解説で、学習を楽しく進めることができています。
恐縮ですが、一点ほどご質問させていただきたく存じます。

私は0.1[s]刻みの不規則な振動を示す時系列に対して、ローパスフィルタをかけてみました。
すると”ValueError: filter critical frequencies must be greater than 0”というエラーが返されました。
通過域端周波数および阻止域端周波数を1Tほどまで変化させましたが、同様のエラーが返されてしまいます。
素人質問で恐縮ですが、お返事いただけますと幸いです。よろしくお願いいたします。

以下、使用した時系列データになります。
23.49,19.142,19.234,24.107,17.278,19.816,25.458,13.858,21.623,26.405,・・・（以下同様のオーダー）

返信
1. wat より:
  
  2022年9月7日 9:31 PM
  
  ご訪問ありがとうございます。
  0.1[s]刻みということは、10[Hz]でサンプリングされたデータということになります。
  ローパスは何[Hz]でかけましたでしょうか？
  
  ナイキスト周波数=サンプリング周波数/2なので、通常はこの範囲でフィルタリングします。
  このエラーは周波数を高く設定した時に発生するようですので、サンプリングと設定値の関係を調査するのが良いでしょう。
  
  また、このエラーは本質的にはWnが0以下になってしまったという意味ですので、
  print(Wn)
  を使ってWnが負になっていることも確認できると思います。
  正規化された周波数Wnはその他、gpass, gstopの影響も受けます。
  
  以上、ご確認お願いいたします。
  
  返信
  1. CCC より:
    
    2022年9月22日 3:00 PM
    
    ご返信ありがとうございます。
    お返事が遅くなってしまい、申し訳ございません。
    
    ローパスの通過域端周波数を0.5[Hz]に設定したところ、問題なくフィルタをかけることができました。ありがとうございます。
    重ねてとなり恐縮ですが、質問をさせていただきたく存じます。
    今回の場合では 0<=fp_lp<=ナイキスト周波数の範囲で通過域端周波数を設定することが正しいのでしょうか？
    
    初歩的な部分かもしれませんが、お返事いただけますと幸いです。
    
    返信
    1. wat より:
      
      2022年9月23日 1:14 PM
      
      問題なく動作したとのこと、こちらこそご連絡ありがとうございます。
      
      >>今回の場合では 0<=fp_lp<=ナイキスト周波数の範囲で通過域端周波数を設定することが正しいのでしょうか？その理解でご使用頂いて問題ないと思います。但し、実際は正規化周波数wnで計算をしているので、gpassやgstopの値次第で端っこの正常動作範囲が変化します。（これ以上の専門的な説明がまだできませんが…）何かおかしいと思ったらprint()で変数の中身を見ながら調べていく…というのは便利なので是非今後のご参考にしてください！
      
      返信
      1. CCC より:
        
        2022年9月26日 10:15 AM
        
        質問への丁寧なお返事、ありがとうございます。
        これからも勉強を続けていきたいと思います。
        また、今後の記事も楽しみにしております。
      2. wat より:
        
        2022年9月26日 11:07 PM
        
        ありがとうございます。
        こちらも勉強ブログなので、学習した内容は記録していく予定です。
        リクエストや質問、疑問は記事のヒントになりますのでこれからもよろしくお願い致します！

この記事の対象者

とにかくフィルタ処理をしたい人

Pythonワカランな人

本記事の目標

csvファイルの複数信号を一度にフィルタ処理する

もっと詳しいフィルタ処理の記事を読みたい人は…

ローパスフィルタ(LPF)

ハイパスフィルタ(HPF)

バンドパスフィルタ(BPF)

バンドストップフィルタ(BSF)

検証済の動作環境

PC

Python環境

環境構築

Pythonのインストール

統合開発環境(IDE)のインストール

外部ライブラリのpipインストール

pip概要と外部ライブラリのインストール方法

プロキシエラーになる場合

csvをフィルタ処理するPythonコード

準備するcsvファイル【ダウンロード可】

全コード【コピペ・2次利用可】

実行結果

フィルタ後のcsvファイル

フィルタ前後の時間波形比較

csvをフィルタ処理するPythonコード(フーリエ変換機能付き)

全コード【コピペ・2次利用可】

実行結果

ローパスフィルタ後の周波数波形確認

ハイパスフィルタ後の周波数波形確認

バンドパスフィルタ後の周波数波形確認

バンドストップフィルタ後の周波数波形確認

まとめ

関連リンク

csvからフーリエ変換するコード

csvから逆フーリエ変換するコード

SNSでもご購読できます。

コメント

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル