
WATLABブログでは時間波形の抽出、オーバーラップ処理、窓関数処理を紹介して来ました。この記事ではそれらのまとめとして、信号処理分野の代表的な計算であるFFT(高速フーリエ変換)を説明します。
こんにちは。wat(@watlablog)です。
いよいよここまで来ました。これまで時間領域の前処理技術を習得して来ましたが、今回はFFTをかけて周波数領域を分析できるようになります!
周波数分析概要とFFTコードの例
時間波形と周波数波形の関係とFFTの威力
当WATLABブログでは信号処理について僕自身が勉強しながら記事を書いています。
信号処理を行う主な目的の一つに周波数分析があります。
周波数とは1秒間に何回振動しているかを数えたものです。そのため、当然時間領域の振動と関係を持っており、図にすると以下のようになります。

上図は単一のサイン波\(y(t)=Asin(2\pi ft)\)の時間波形と周波数波形を説明しています。波の周期\(T\)と周波数(振動数)\(f\)には\(f=1/T\)の関係で変換可能であり、振幅\(A\)がわかれば何も難しい理論を要するFFT(Fast Fourier Transform)を使わずとも周波数波形をプロットすることが可能です。
ちなみに周波数波形から時間波形に変換することを逆FFT、またはIFFT(Inverse Fast Fourier Transform)と呼びますが、上図の単一サイン波のように単純なものは紙とえんぴつさえあればプロットできますね。
ではもっと波形を複雑にしてみましょう。複雑な波形でも時間波形と周波数波形の関係は下図のように成立します。
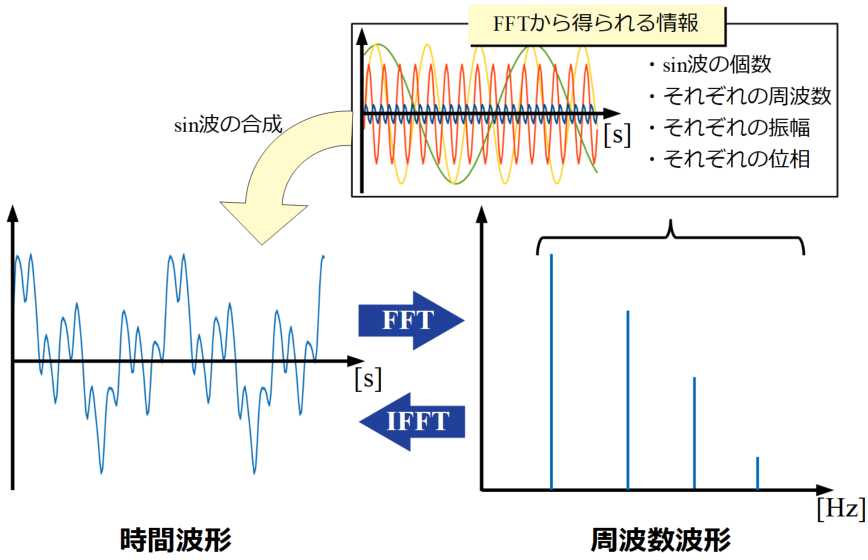
この図の時間波形は、実際にExcelで4つのサイン波を、振幅と位相を変えて足し合わせたものです。
たった4つの波形を合成させただけでも、もはや人間の目と頭では正確に周波数波形を描くことはできません!
FFTからは主要なサイン波の個数や、それぞれのサイン波の振幅と位相の情報を得ることができます。これらの情報があると、実際の時間波形がどのような振動成分で構成されているかがわかるので、あらゆる分析に使われています。
例えば、ある構造物の振動原因調査や、どんな材料でできているのかといった工学的な分野に多く使われています。医療現場におけるMRIやCTスキャンの画像処理にもフーリエ変換は活用されています。
今回は以下の図の時間波形を分析してみます。0.5秒程度のデータですが、データサンプル数は12800あります。
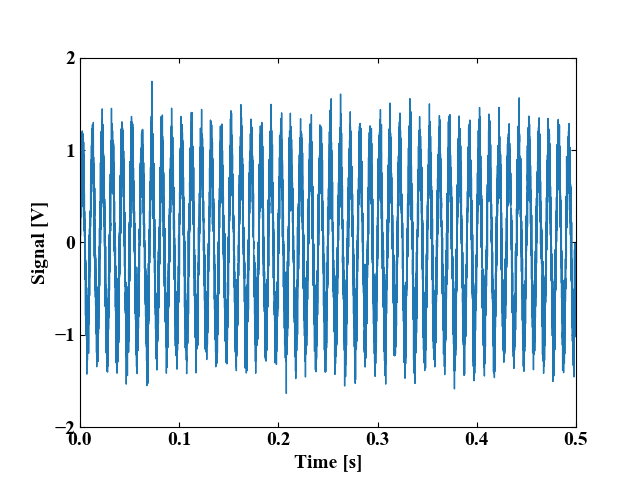
波形生成コードは以下です。
|
1 2 3 4 |
import numpy as np samplerate = 25600 x = np.arange(0, 12800)/samplerate #波形生成のための間軸の作成 data = np.sin(2.0 * np.pi * 100 * x) + 0.2 * np.random.randn(len(x)) #サイン波にランダム成分を重畳 |
簡単にFFTする方法(1フレームFFT/DFT)
平均化FFTをする前に、まずは簡単に入力した信号をそのままフーリエ変換する方法を紹介します。
以下にscipyのfftpackを使ったフーリエ変換コードの例を示します。
このコードをそのままコピぺして実行すると、上記の時間波形を周波数分析したグラフが出力されます。
def関数ではspectrumの部分がフーリエスペクトルの結果です。1行で完了してしまうほど簡単ですが、このspectrumは複素数です。
ampで振幅成分、phaseで位相を計算しています。また、freqは周波数軸を作成しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt # フーリエ変換をする関数 def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成 return spectrum, amp, phase, freq samplerate = 25600 x = np.arange(0, 12800)/samplerate #波形生成のための間軸の作成 data = np.sin(2.0 * np.pi * 100 * x) + 0.2 * np.random.randn(len(x)) #サイン波にランダム成分を重畳 # フーリエ変換する関数を実行 spectrum, amp, phase, freq = calc_fft(data, samplerate) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Amplitude') # スケールの設定をする。 ax2.set_xticks(np.arange(0, 1000, 100)) ax2.set_xlim(0, 500) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, data, label='Time waveform', lw=1, color='red') ax2.plot(freq, amp, label='Amplitude', lw=1, color='blue') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
以下の図が結果です。上に時間波形、下に周波数波形を示しています。たまにFFTした結果で振幅成分がおかしいネット記事がありますが、振幅成分も生成したsin波の振幅1を示しています。
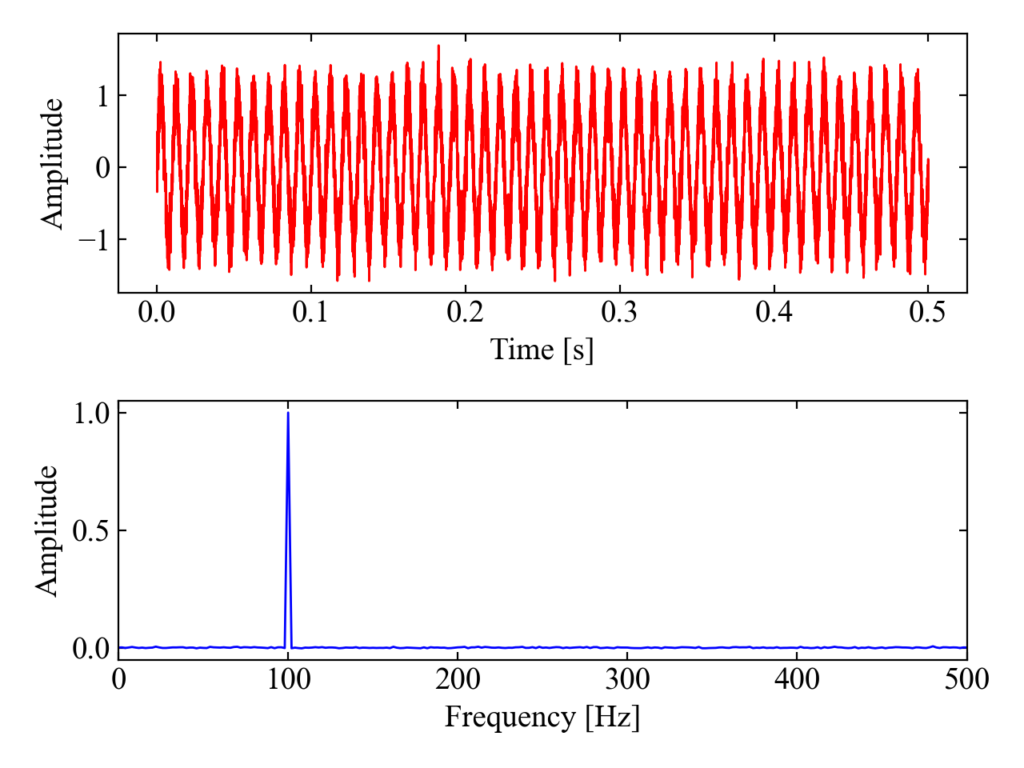
本方法では実はサンプル数はFFTの制約である2の累乗個でなくても機能します(その場合はDFTになるのかな?)
しかし信号の長さが変わると周波数分解能が変わってしまったり、ノイズに弱かったりとなかなか定量評価が難しい所があります。
次は、ある区間毎にフレームを抜き出し、平均化しながらFFTをするためのデータの前処理、そして平均化FFTのコードを紹介します。
平均化FFTのための前処理
波形分割・抽出・オーバーラップ
周波数分析をする場合、計測する対象のデータはある程度一定の振動をしている区間を想定することが多くあります。
実際の振動現象は式で記述するよりも多くのばらつきを含むので、ある程度の時間長分データを計測し、その後に平均化する必要があります。
FFTはそのアルゴリズムからデータ長が2の累乗(\(2^n\))である必要がありますので、平均化に使うデータフレームのサイズも1024や4096…といったものをよく選びます。
この際にオーバーラップという手法を用いる方法と自作したコードを前回記事で紹介しましたので、是非以下の記事を参照下さい。
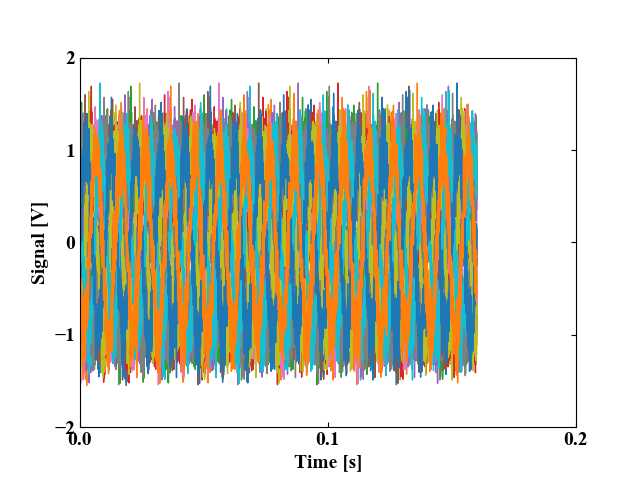
この記事では0.5秒の波形に90%のオーバーラップ率でデータを4096個ずつ抽出した22個の波形データを分析します。以下がオーバーラップ波形です。
オーバーラップ処理のコード
オーバーラップ処理のコードは以下です。可読性の良さを重視して関数化しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import numpy as np #オーバーラップ処理 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate #全データ長 Fc = Fs / samplerate #フレーム周期 x_ol = Fs * (1 - (overlap/100)) #オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap/100))) / (Fc * (1-(overlap/100)))) #抽出するフレーム数(平均化に使うデータ個数) array = [] #抽出したデータを入れる空配列の定義 #forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) #切り出し位置をループ毎に更新 array.append(data[ps:ps+Fs:1]) #切り出し位置psからフレームサイズ分抽出して配列に追加 return array, N_ave #オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする |
窓関数をかける
波形から分析用のデータを抽出したら、窓関数を使ってFFTのための前処理をします。
窓関数については以下の記事で内容とコードを紹介していますので、こちらも必要に応じて参照下さい。
ちなみに、窓関数は自作することも可能です。
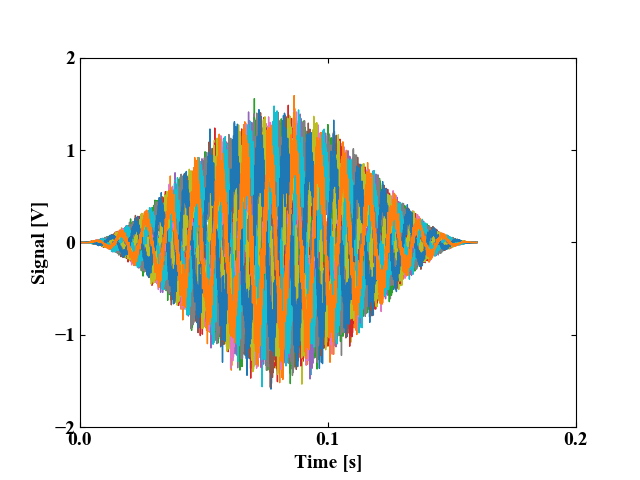
先ほどのオーバーラップ波形にハニング窓をかけた結果が以下の図です。
窓関数処理のコード
窓関数処理のコードは以下です。こちらも関数化しています。
|
1 2 3 4 5 6 7 8 9 10 |
#窓関数処理(ハニング窓) def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) #ハニング窓作成 acf = 1 / (sum(han) / Fs) #振幅補正係数(Amplitude Correction Factor) #オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han #窓関数をかける return data_array, acf |
平均化FFTのコード
ようやく平均化FFTの出番です。ここでは巷の商用ツールで計算されているようなオーバーラップ処理と窓関数を考慮した周波数平均されたFFTを目指しています。
しかし、このコーディングの最中に筆者自身が直面した壁がありましたので、以下に注意点として残して大きます。まだ真の理解を得たわけではありませんが、今後のキーワード検索のヒントになればと思います。
※理解がクリアになった時点でまた記事にまとめたいと思います。
注意点
窓関数を使った場合は補正が必要
窓関数は元の波形を歪ませてしまいます。特に振幅を小さくしてしまうので、FFTで振幅成分を出す時は補正が必要です。
補正については以下の記事に別途まとめましたので、参照下さい。
FFTで振幅を出す時に一種の正規化が必要
本ブログは筆者がネットを彷徨い、書籍をあさりながら勉強した結果をアウトプットしています。
FFT計算では主に振幅成分を評価することが多いと思いますが、正しい振幅を得るためにFFTの計算式を「サンプル数の半分で割る」という処理を色々な方が行っていました。コードにすると以下です。
|
1 |
np.abs(fftpack.fft(data_array[i])/(N/2) #Nがサンプル数 |
こちらも理論波形を使って検証してみるとやはりこの(\(N/2\))の割り算が無いと正しい振幅成分が得られないという結果を得ました。
その理屈を調べていたのですが、中々僕程度の頭にはピンときませんでした。但し、以下のページの質疑応答がおそらく核心部分と思われますので、引用させて頂きます。
質問
yf = fftpack.fft(y)/(n/2)
で、なぜn/2で割るのかがよくわかりません。回答
teratail:Pythonでフーリエ変換する方法
n/2のうちのnはデータ点数で、同じ区間でも解像度が高くなるほど積分値が大きくなってしまうことへの補正です。2は折り返し信号の分をサボったためです。fftshiftを使ったとすれば、正の周波数の負の周波数ではx=0のy軸に対して対称になっていると思います。もう少し細かく見ると、cos項(複素フーリエ係数の実数部分)は正負で同じ値なのに対して、sin項(複素フーリエ係数の虚数部分)は符号が反転していると思います。
少し脱線しましたが、本来ならば同じ周波数の振幅成分が正負に分かれて存在したはずのところを、参考にしている記事では正の部分しか扱っていません。コレ自体はよく行われることです。ただし、本来ならばデータ点数nで割っておけばいいだけのところを、負の周波数成分が無視しているために振幅が合わなくなってしまいます。この点を考慮してnではなくn/2で割っているのです。
処理の過程で、サンプル数が多くなると、積分値(離散データなのでΣ計算)が大きくなるというのはイメージが付きます。そのため「Nで割る」という一種の正規化は必要と思いますが、N/2にする意味はフーリエ変換の中身をもう少し理解する必要があります。
ネットに多く溢れているPythonのFFTコードは最後に辻褄を合わせている…ということだと考えられます。高速フーリエ変換の中身に言及する記事が書ければ、再度理解を深めるためにコードを見直したいと思います(できるかな?)。
平均化は算術平均?パワー平均?
僕も無知で間違っていましたが、信号処理分野の平均化の計算方法は奥が深いです。音圧のように、dB基準値を持ちdBで評価する物理量の場合はパワー平均(エネルギー平均、デシベル平均とも呼ぶ)を求めるのが正しい平均化との事。
参考文献:小野測器「dB(デシベル)」とは
規格にもよるそうですが、デシベルの平均は算術平均を用いず、以下の式で行います(\(L_{i}\)(デシベル値)の平均)。
FFT後の振幅値(リニア値)の算術平均後にデシベルに変換しても、デシベル平均の式で得られる結果にはなりませんので、平均化FFTを行う場合には注意が必要です。
デシベルにする前に二乗してから(パワースペクトルにしてから)算術平均をすると、先にデシベル変換してから上式でデシベル平均を行った結果と一致します(表計算ソフト等で試してみて下さい)。
FFT処理の全コード
前置きが長くなりましたが、以下に今回のFFTを実現する全コードを示します。
ファイルはメイン(main_fft.py)と関数(fft_function.py)に分けて、メインを実行する方法にしました。
まずは関数を集めたファイルです。詳細は各行にコメントを記載しましたので参考にして下さい。
今回dB変換をしていませんが、平均化はパワー平均です(但し、ここでは振幅成分を計算したかったのでルートでパワースペクトルを振幅スペクトルにしています)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
import numpy as np from scipy import signal from scipy import fftpack #オーバーラップ処理 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate #全データ長 Fc = Fs / samplerate #フレーム周期 x_ol = Fs * (1 - (overlap/100)) #オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap/100))) / (Fc * (1-(overlap/100)))) #抽出するフレーム数(平均化に使うデータ個数) array = [] #抽出したデータを入れる空配列の定義 #forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) #切り出し位置をループ毎に更新 array.append(data[ps:ps+Fs:1]) #切り出し位置psからフレームサイズ分抽出して配列に追加 return array, N_ave #オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする #窓関数処理(ハニング窓) def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) #ハニング窓作成 acf = 1 / (sum(han) / Fs) #振幅補正係数(Amplitude Correction Factor) #オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han #窓関数をかける return data_array, acf #FFT処理 def fft_ave(data_array,samplerate, Fs, N_ave, acf): fft_array = [] for i in range(N_ave): fft_array.append(acf*np.abs(fftpack.fft(data_array[i])/(Fs/2))) #FFTをして配列に追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 fft_axis = np.linspace(0, samplerate, Fs) #周波数軸を作成 fft_array = np.array(fft_array) #型をndarrayに変換 fft_mean = np.sqrt(np.mean(fft_array ** 2, axis=0)) #全てのFFT波形のパワー平均を計算してから振幅値とする return fft_array, fft_mean, fft_axis |
続いてメインの動作を記述したファイルです。後半のグラフ描画域が少し長めですが、基本的に関数を使うことによりメイン計算はシンプルになりました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 |
import fft_function import numpy as np from matplotlib import pyplot as plt samplerate = 25600 x = np.arange(0, 12800)/samplerate #波形生成のための間軸の作成 data = np.sin(2.0 * np.pi * 100 * x) + 0.2 * np.random.randn(len(x)) #サイン波にランダム成分を重畳 Fs = 4096 #フレームサイズ overlap = 90 #オーバーラップ率 #作成した関数を実行:オーバーラップ抽出された時間波形配列 time_array, N_ave = fft_function.ov(data, samplerate, Fs, overlap) #作成した関数を実行:ハニング窓関数をかける time_array, acf = fft_function.hanning(time_array, Fs, N_ave) #作成した関数を実行:FFTをかける fft_array, fft_mean, fft_axis = fft_function.fft_ave(time_array, samplerate, Fs, N_ave, acf) t = np.arange(0, Fs)/samplerate #グラフ描画のためのフレーム時間軸作成 #ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Signal [V]') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Signal [V]') #データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 2, 0.04)) ax1.set_yticks(np.arange(-5, 5, 1)) ax1.set_xlim(0, 0.16) ax1.set_ylim(-3, 3) ax2.set_xticks(np.arange(0, samplerate, 50)) ax2.set_yticks(np.arange(0, 3, 0.5)) ax2.set_xlim(0,200) ax2.set_ylim(0, 1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 for i in range(N_ave): ax1.plot(t, time_array[i], label='signal', lw=1) ax2.plot(fft_axis, fft_mean, label='signal', lw=1) fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
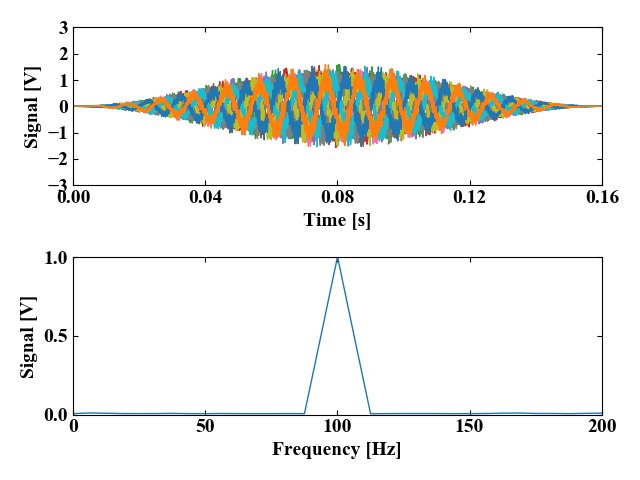
このコードを実行すると以下の結果が得られます。
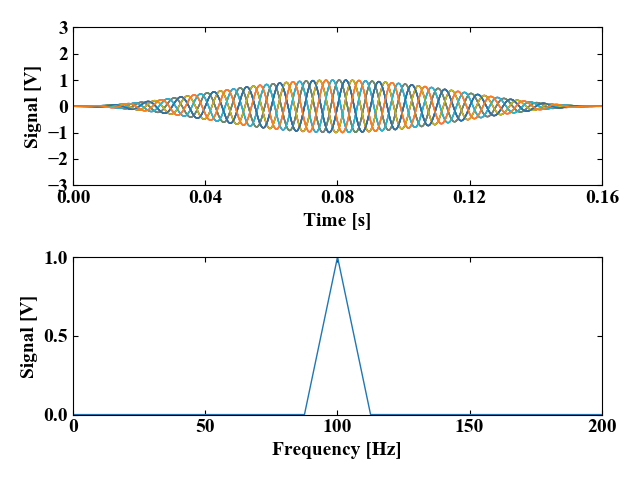
ちなみに、ノイズ成分を0(ランダム波形の係数=0)にすると以下の波形になります。
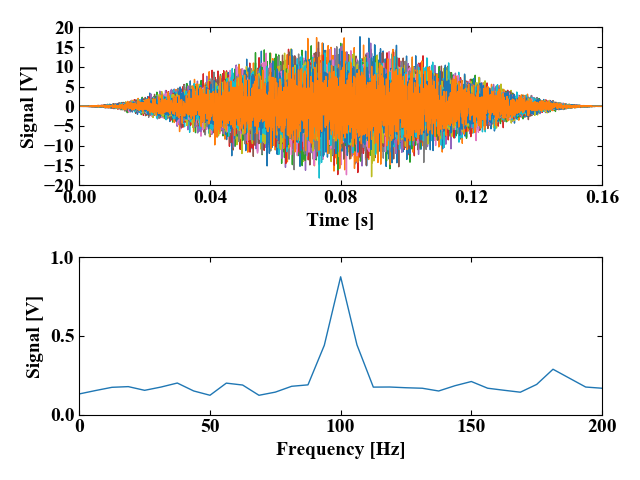
ノイズ成分を思い切り上げてしまう(ランダム波形の係数=5)と以下の波形になります。このレベルになると、主信号であるサイン波の振幅にノイズが影響を与えてしまうようです。そして基本周波数100Hz以外のレベルが増加している傾向が明確に表れて来ました。一般的には、この部分をノイズフロアと呼びます。
色々な関数のFFT結果
ここではせっかく覚えたフーリエ変換を使って色々な関数の周波数分析をしてみましょう。
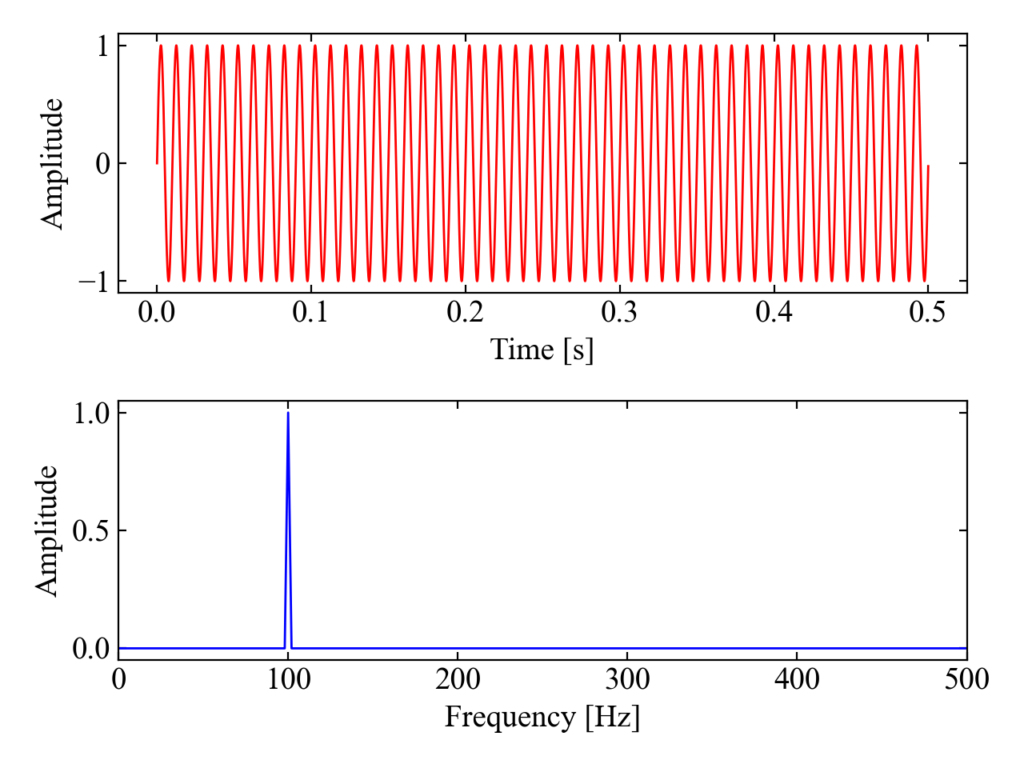
正弦波(\(\sin \theta\))
周波数分析といったらまずは正弦波、というくらいテストされている関数。上記コードのdata部分を以下のように変更する事で今回は振幅1、周波数100Hzの正弦波を作ってみます(ノイズは含ませないパターンです)。
|
1 2 |
# sin波 data = np.sin(2.0 * np.pi * 100 * x) |
100Hzに単一のピークが出てくる結果を得ました。
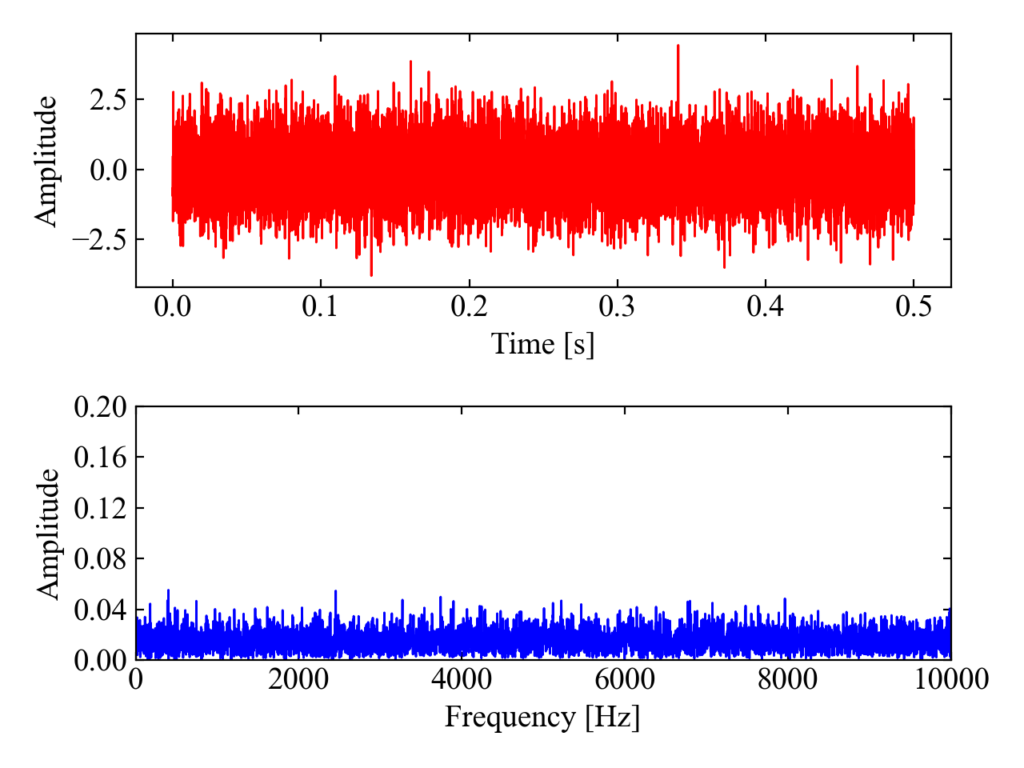
ガウシアンノイズ
ガウシアンノイズはガウス分布を持つノイズですが、ホワイトノイズとも呼ばれます。詳しくは「Pythonでガウス分布を持つノイズの作り方と調整方法」で書いていますが、dataを以下のコードに変更するだけです。
|
1 2 |
# ガウシアンノイズ data = np.random.normal(loc=0, scale=1, size=len(x)) |
以下がガウシアンノイズの周波数分析結果です。正弦波と違って全周波数で特にピークを持たないのが特徴です。
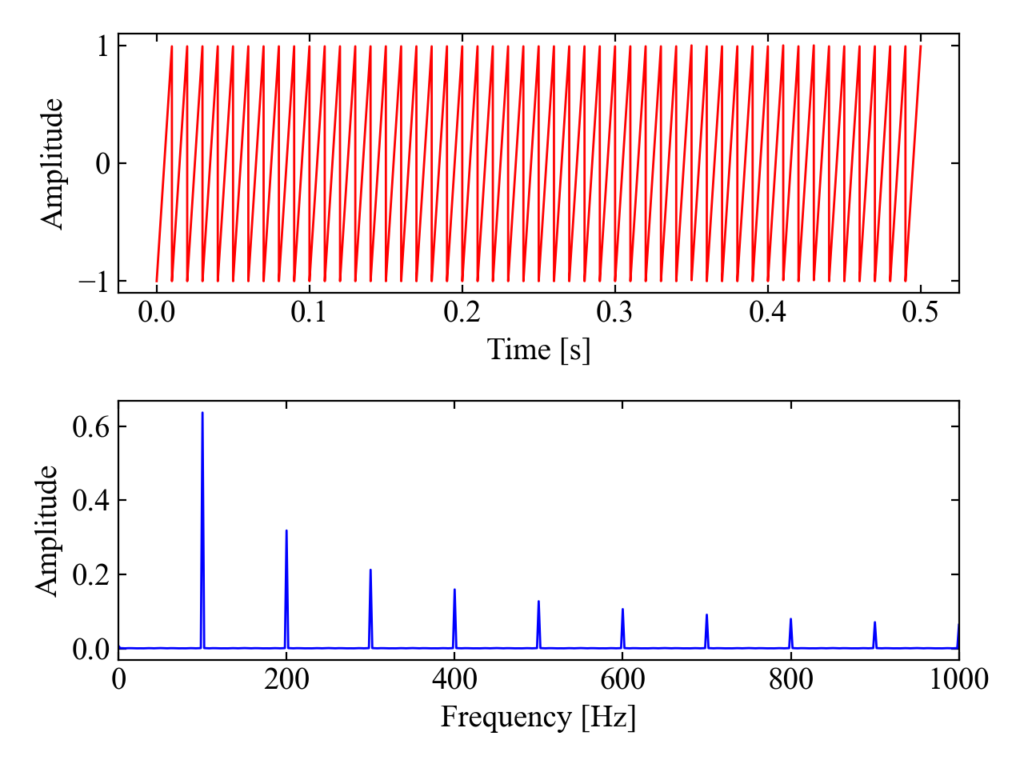
のこぎり波
のこぎり波は「Pythonでのこぎり波を生成!次数の高調波成分を見てみた」で書いていますが、以下のコードで生成可能です。振幅1、周波数100Hzとしています。
|
1 2 3 |
# のこぎり波 from scipy import signal data = signal.sawtooth(2 * np.pi * 100 * x) |
以下がのこぎり波の周波数分析結果です。100Hzの基本次数の2倍、3倍…で次数が発生しているのが特徴です。これらの基本次数以外の次数の事を高調波と呼びます。
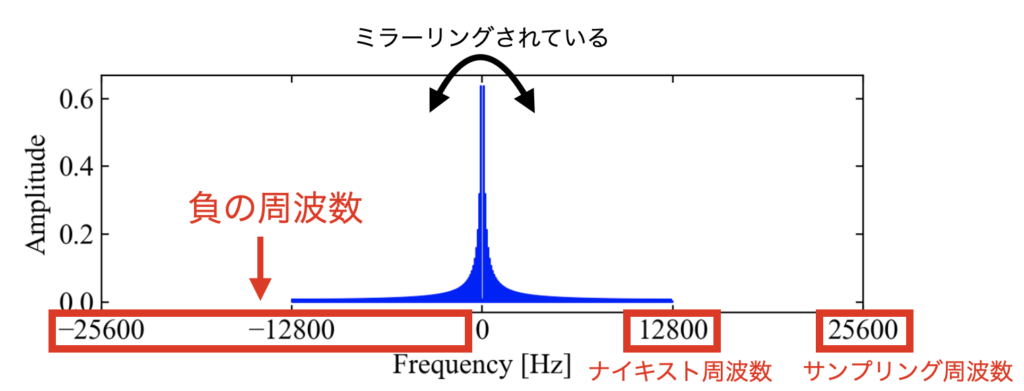
補足:ミラーリングと周波数軸について
ミラーリングとナイキスト周波数
先ほどまでは周波数分析の結果として、興味帯域しか表示させていませんでしたが、全周波数帯域を表示させると以下の図のようになります(ここではのこぎり波の結果を例に説明します)。
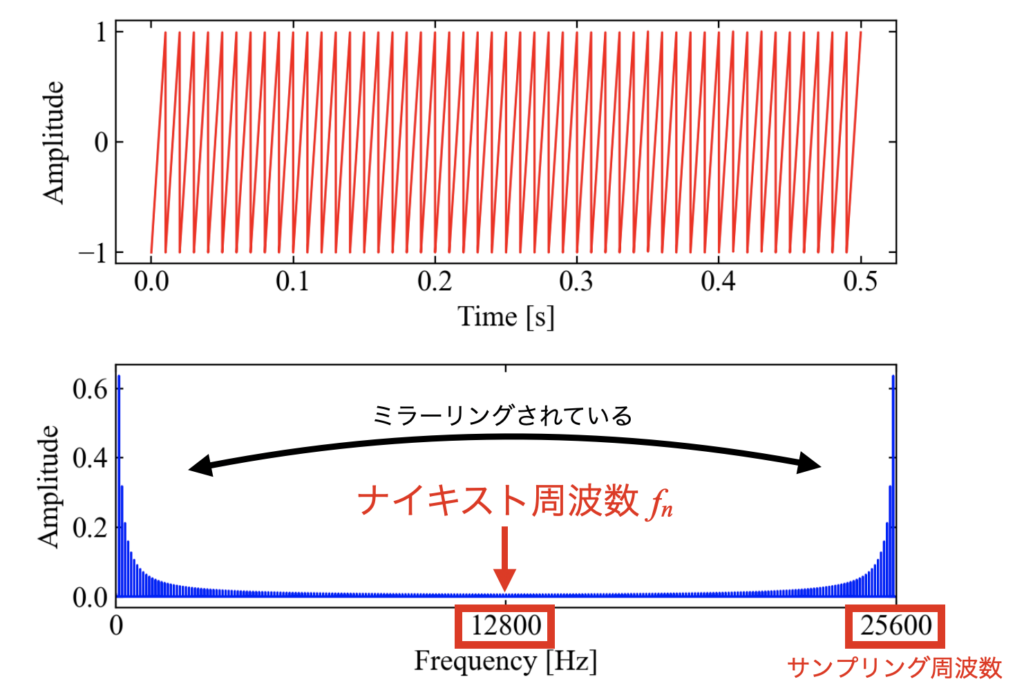
このように、全周波数帯域を表示させると、みかけ上はサンプリング周波数までデータが存在していますが、サンプリング周波数の半分であるナイキスト周波数\(f_{n}\)を境に折り返されているだけの波形となっている事に気付きます。
このピークの事をミラーリングピークと言ったり、鏡像ピーク、共役鏡像と言ったりするそうです。
そのため、「どの周波数でどれだけの振幅で振動しているか」、といった分析を行う時はこのナイキスト周波数\(f_{n}\)までを扱い、それ以上は切り捨てるという事が行われます。
負の周波数とは?
この記事では便宜上周波数軸をlinspace(0, samplerate, Fs)と正の数値のみで作成していました。
しかし、フーリエ変換は実際は複素数(二乗して負になる数)の計算を行っており、下図のようにフーリエ変換の性質から本来周波数軸は負の値も持ちます(これが本来の姿と思います)。
以下の外部リンクが参考になります(理系なのに数学苦手なので丸投げ!)。
入力データが実数である場合にのみ、FFTの結果が(共役対称のように)ミラーリングされることに注意してください。
qstack:FFTが「ミラーリング」されるのはなぜですか?
厳密に実数の入力データの場合、FFT結果の2つの共役鏡像は、複雑な正弦波の虚数部を打ち消すため、厳密に実数の正弦波(小さな数値の丸めノイズを除く)になります。実際の正弦波。
FFTの結果が共役鏡像化されていない場合、厳密な実数値ではなく、複素数値(非ゼロの虚数成分)を持つ波形を表します。
→詳細は式で。
負の周波数成分が出てくる理由は複素フーリエ級数展開を学ぶことで理解が深まるかも知れません。色々見た結果、ヨビノリたくみさんの講義「【大学数学】フーリエ解析入門④(フーリエ級数展開Ⅳ)/全5講【解析学】」がわかりやすいと思いました。
負の周波数を求めるコード:fftpack.fftfreq()
負の周波数はlinspaceでも作成する事が出来ますが、scipyのfftpackでフーリエ変換しているのであれば、fftpack.fftfreq()を使った方が効率的です。
以下のコードは本記事の一番上に紹介していた単一フレームのフーリエ変換を行う関数ですが、freqの部分をfftpack.fftfreq()を使って書き直しています。
fftfreq()はフーリエスペクトルの長さと信号の時間刻みdを引数として計算されます。
|
1 2 3 4 5 6 7 8 9 |
# フーリエ変換をする関数(負の周波数も計算するバージョン) def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = fftpack.fftfreq(len(spectrum), d=1/samplerate) # 周波数軸を作成 return spectrum, amp, phase, freq |
負の周波数が必要になる場面とは?
負の周波数なんて周波数分析で見ないんだからどうでも良いじゃないか!
…と考えがちですが、実は結構重要なんです。
確かに、単純に一番振動している周波数と振幅を分析したいだけであればよくネット記事で語られている正方向の周波数軸がナイキスト周波数分だけあれば問題無いです。
しかし、フーリエスペクトルを使って別途工学演算を行う場合に負の周波数が必要になる事が多々あります。
「FFT波形を微積分!Pythonで周波数軸微積分をしてみた」では、フーリエ変換の結果のみを使って微分積分の演算をしています。
この周波数軸演算では角振動数\(\omega\)を使うので、負の周波数と正の周波数を含む正しい周波数軸を計算で使わないと全く異なる演算結果を出してしまいます(この記事を書いた時に僕はそれがわからずハマりました…)。
もしフーリエ変換の結果を使って工学的な計算を行う場合は注意しましょう。
まとめ
このページでは、1フレームしか無い時間波形のFFTに加えて、任意長さの時間波形から平均化FFTを求める方法も学びました。
平均化するためには複数のデータフレームが必要で、元の時間波形からフレームをオーバーラップさせながら抽出することで必要な情報をできるだけ含んだ時間波形フレームを作成しました。
窓関数はハニング窓を各時間波形にそれぞれかけ、その時間波形を一つ一つFFT処理しました。このFFT処理時には窓関数による振幅を補正する係数ACFを使いました。
全てのFFTは周波数軸で平均化することにより一つの結果を算出しています。
学んだフーリエ変換を使って様々な関数を周波数分析してみると、それぞれ波形の特徴を捉える事が出来ました。
おまけとして周波数軸に関する注意点を述べました。本ページでPythonのFFTイメージを掴んで頂けたら幸いです。
参考:フーリエ変換の応用例を紹介
逆高速フーリエ変換(IFFT)
フーリエ変換した結果を逆フーリエ変換する事で再び時間波形に戻す事が可能です。
周波数領域でフィルタリングしたり何か処理をした後に時間波形に戻すといった使い道があります。
逆フーリエ変換については「PythonでFFTとIFFT!逆フーリエ変換で時間波形を作る」に詳細を書きましたので参考にして下さい。
2Dフーリエ変換
「Pythonで2Dフーリエ変換!画像フィルタリングをする方法」という記事で画像データのフーリエ変換をやってみました(2Dのフーリエ変換)。
本記事の周波数軸に関する説明を読んでからこの記事を読むと、一段と理解の助けになると思います。参考までに。
スペクトログラム分析
スペクトログラムとは時間✖️周波数✖️振幅と3次元的にフーリエ変換を並べたものです。
次数の時間変化を分析する事が出来るため、非常に幅広く使われている分析手法です。是非「Pythonで音のSTFT計算を自作!スペクトログラム表示する方法」をご覧下さい。

ヒルベルト変換
ヒルベルト変換とはFFTとIFFTを使い時間波形の包絡線を書く事が出来るものです。フーリエ変換を覚えるとこんな事も出来きます。
結構簡単なのでやってみたい方は「Pythonでヒルベルト変換!時間波形の包絡線を求める方法」をご覧下さい。
ケプストラム分析
フーリエ変換の応用として音声分野では声帯情報を分離するケプストラム分析というものがあります。
こちらもフーリエ変換を巧みに使っていますので、ご興味のある方は「Pythonでケプストラム分析!音声から声帯情報を取得してみた」をご覧下さい。
周波数応答関数(FRF)とコヒーレンス関数
フーリエ変換を2つの信号に対して行い、クロススペクトルやパワースペクトルを駆使すると入力と出力に関する周波数応答関数(FRF)を算出する事が出来ます。
これも工学的な分析でよく使われるので、コードを確認したい方は是非「Pythonで伝達関数!2つの信号の周波数応答関数を計算する方法」の記事をご覧下さい。
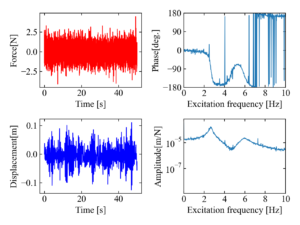
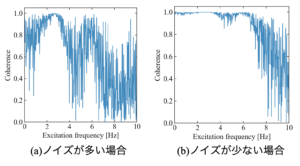
周波数応答関数は同じくフーリエ変換を応用して計算するコヒーレンス関数も併用すると、より確度の高い分析が可能です。
コヒーレンス関数については「Pythonでコヒーレンス関数!FRFのノイズ成分を評価する方法」をご覧下さい。
オーバーラップから窓関数、平均化FFTを自分で実装することができたぞ!
今回の学習で比較的自由に信号を取り扱えるようになってきた気がするので、さらに高度なことにも挑戦しよう!
X(旧Twitter)でも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
はじめまして。スピネルと申します。
現在、フーリエ解析について学んでいる大学生です。
pythonはまだ初心者でコードを参考にさせて頂いています。
そこで質問ですが、「import fft_function」の部分でモジュールエラーが起きてしまったので、
pipコマンドでインストールしようとしたところ、コマンドが見つからないと出てしまいました。
大変恐縮ですが、「fft_function」について詳しく教えて頂けたら幸いです
ご訪問ありがとうございます。
わかりにくくて申し訳ございません!
ここでは「fft_function.py」という関数だけを集めたPythonファイルを別途自分で作成し、それをメインのPythonファイルでimportするという方法をとっています。
そのためpip installは必要ありません。
初めましてゼロークです。業務で手っ取り早くpythonでFFT平均処理をするコードを探していていたので助かります。(c系しかやってこなかったので)
さて、「サンプル数の半分で割る」理由について、更新がされていなかったので、以下の参考URLを記述しておきます。
既にご存じでしたら無視して頂いて構いません。
https://www.onosokki.co.jp/HP-WK/c_support/newreport/analyzer/FFT3/fft_5.htm
https://www.onosokki.co.jp/HP-WK/c_support/newreport/analyzer/FFT1/fft_2.htm#mark6
→ 2.7 波形表現<波形の積>にジャンプしているはず
https://www.onosokki.co.jp/HP-WK/c_support/newreport/analyzer/FFT2/fft_3.htm
ゼローク様、ご訪問ありがとうございます。
また、大変貴重なコメントも誠にありがとうございました。
こちらの小野測器さんのページは初見でして、まだあまり詳細をみれていませんが、連続関数の場合でT/2で元の振幅…という部分でしょうか。
じっくり読んでいけば僕でも理解できそうな内容で勉強になります!
(実は我流でやっていただけなのでなかなか進んでいませんでした)
本当に助かります。ありがとうございます。
先に文章が長くなり申し訳ありません。
dB値の単純平均を行っていますが、0dB基準値(1Vrms、2*10^-5Paなど)を使用するものは絶対レベルとなるため、パワー平均で計算する必要があります。詳しくは下記URLをご参照ください。
https://www.onosokki.co.jp/HP-WK/c_support/newreport/decibel/dB.pdf
https://www.onosokki.co.jp/HP-WK/c_support/faq/fft_common/fft_spectrum_7.htm
https://www.onosokki.co.jp/HP-WK/c_support/faq/fft_common/fft_spectrum_6.htm
このページでは音圧レベルを測定しているため、絶対レベルとなりパワー平均で計算する必要があります。
例を挙げると、音圧が0.1Pa、0.2Pa、0.3Paの平均を取ろうと思ったとき、以下のように結果が異なります。
A) dB値の算術平均
{ 20*log10(0.1/2*10^-5) + 20*log10(0.2/2*10^-5) + 20*log10(0.3/2*10^-5) } / 3 = 79.16707509[dB]
B) 振幅スペクトルの算術平均後にdB値(パワー値)に変換
(0.1 + 0.2 + 0.3) / 3 = 0.2
20*log10(0.2/2*10^-5) = 80[dB]
C) パワースペクトルに対してdB計算
(0.1^2 + 0.2^2 + 0.3^2) / 3 = 0.046666667
10*log10(0.046666667/(2*10^-5)^2) = 80.6694679[dB]
なので、以下の手順でコードを修正する必要があるかと思います。
① オーバーラップで取得した振幅スペクトルの配列全てを二乗してパワースペクトルに変換
② 手順①に対して算術平均する(※1)
③ 手順②で取得した平均パワースペクトルをdB計算する(※2)
※1 小野測器HPのdB計算で説明している10^(dB値/10)の計算はパワースペクトルの値 / 0dB基準値^2が算出されることを意味します。手順③で0dB基準値を使用するため、前述したc)の方法のようにパワースペクトルを平均したものに0dB基準値でdB計算をすれば良いことになります。
※2 パワースペクトルの場合は、0dB基準値を2乗したもので算出するので2*10^-5なら(2*10^-5)^2を使い、20log10では無く10*log10で計算します。
振幅スペクトルをパワースペクトルとして表示変換する場合に限っては、振幅スペクトルの値を使って20*log10(振幅/0dB基準値)でも結果は同じとなります。
余談ですが、スペクトル平均の方法はその他にもあり、用途に応じて使い分けます。以下URLをご参照ください。
https://www.onosokki.co.jp/HP-WK/c_support/faq/fft_common/fft_spectrum_10.htm
こちらもコメントありがとうございます。
A、B、Cの内容、確かに。
この内容はちょっとじっくり読ませて頂いてからコードを見直してみたいと思います。
パワースペクトルの計算方法やdB計算方法はみた事あるレベルでしたが、理解には及んでいなかったようです。
ゼローク様、おそらく専門家とお見受けしました。
当ブログに大変詳細にご教示頂きありがとうございました。
(小野測器さんのページもわかりやすいですが、もしオススメの専門書があったら教えて頂けませんでしょうか…)
はじめまして
不明な点が一つあったのでご質問させていただきます。
フレームサイズのFsのデータ点数はどのように決めればよいのでしょうか
またオーバーラップ率は50%が一般的なのでしょうか
よろしくお願いいたします
ご訪問ありがとうございます。
何度もコメントして頂きすみません!当ブログのコメント欄はスパム防止で承認制のため反映まで時間がかかっていました。
フレームサイズの決め方ですが、以下の観点がすぐに思いつく所です。
①周波数分解能
フレーム周期[s](FFTするフレームの時間長)を長くすると周波数分解能が向上します。
細かい周波数ピークを分析したい時は同一時間刻みであればフレームサイズを大きくします。
②時間変化を捉えられるか
フレームサイズを大きくとって周波数分解能を高めると、フレーム内の信号の変化を捉える事が出来なくなります。
元の信号が時間で変動する場合、フレームサイズを短くする事で変化を捉えた分析が可能です。
STFT等の分析をする事で①と②のトレードオフ関係を体感する事ができるでしょう。
また、オーバーラップは情報の欠如を補うような観点で使用する事が多いです。
例えば、FFTは通常窓関数(ハン窓等)と併用して計算しますが、窓関数をかけると振幅の減衰が発生します。
ハニング窓であれば2/3減衰するので、適切に情報を補おうとすると66.7%ほどのオーバーラップをかけるのが良いとされています。
(綺麗な数にしたいという意味で75%とかもよく使います)
ただ、オーバーラップをかけすぎるとそれだけ平均化回数が増えてしまうので、高速な計算が必要な場面ではかけすぎると重くなってしまうでしょう。
以上、回答になりましたでしょうか?
よろしくお願い致します。
返信ありがとうございます。
スパム防止の件、かしこまりました。
なるほど、そのような観点でフレームサイズを決めれば良いのですね。
ハニング窓では2/3減衰とありますが、これはどのようにして求めれば良いのでしょうか。
また、watさんから信号処理に関して参考になる書籍等ございましたらご教示いただきたいです。
よろしくお願いいたします。
2/3の数字は
「https://www.onosokki.co.jp/HP-WK/eMM_back/emm179.pdf」
の小野測器さんのコラムに書いてありますが、同小野測器さんのWebページで
「https://www.onosokki.co.jp/HP-WK/c_support/faq/fft_common/fft_spectrum_12.htm」
50%程度あれば、という記述もあります。
2/3自体は情報量の問題なので、時間方向にかけるオーバーラップと厳密な関係はないのかも知れません。
こちらも小野測器さんの文献や実際の計測現場で行われている慣習で説明している事が多く、申し訳ございませんがこれ以上詳細までは説明するスキルがありません。
(実際の信号をよく見て適切なパラメータを模索する…というのがやはり必要と思います)
僕は信号処理の基礎としては、
「基本からわかる信号処理 講義ノート」
を購入しましたが、
実践の処理についてはGoogleで「小野測器 ○○」と調べる事が多いです。
結構PDFでコラムがまとまっていますので、是非参考にして下さい。
こんにちは.
Pythonを使い始めたばかりの初心者なのですが,今後FFTを用いる必要があり,こちらのサイトを参照しております.大変勉強になっています.
さて,こちらに挙げられているコードを用いてみたのですが,
メインの動作を記述したコードを実行してみると,
KeyError:ALIGNED
と表示されてしまいます.
データタイプの問題?などと考えたのですが,何度試しても同じエラーが出てしまいます.
何か考えられる原因はありますでしょうか.
ちなみに,数値データの入ったcsvデータを用いました.
ご訪問ありがとうございます。
KeyErrorは辞書型のデータを読み込めない時に発生する例外のようです。
csvはSHIFT-JISで保存されていますでしょうか?
UTF-8等、エンコードの種類によってフォーマットが変わりますので、それで読み込めない可能性もあると思いました。
ご返信ありがとうございます.
csvを確認したところ,UTF-8で保存されていました.
ご確認ありがとうございます。
するとcsv保存時にSHIFT-JISへ変更するか、もしくはコードでSHIFT-JISとなっているところをutf-8にすることで解決する可能性があります。
それでも解決しない場合は他の原因となりそうです。
こんばんは.
csvをSHIFT-JISにしたところうまく行ったみたいです!
ありがとうございます!