
減衰自由振動現象の重要な特性に減衰率があります。減衰特性は物性から求めることが難しいので、実際に系を振動させて測定することが一般的です。ここでは減衰自由振動の波形に対してヒルベルト変換を行い、対数減衰率を計算するPythonコードを紹介します。
こんにちは。wat(@watlablog)です。ここではPythonを使って振動波形から減衰率を測定してみます!
減衰自由振動のおさらい
減衰自由振動とは?
減衰自由振動とは、振動を繰り返すにつれて徐々に振幅が小さくなっていく現象を指します。下図に減衰自由振動の例を示します。
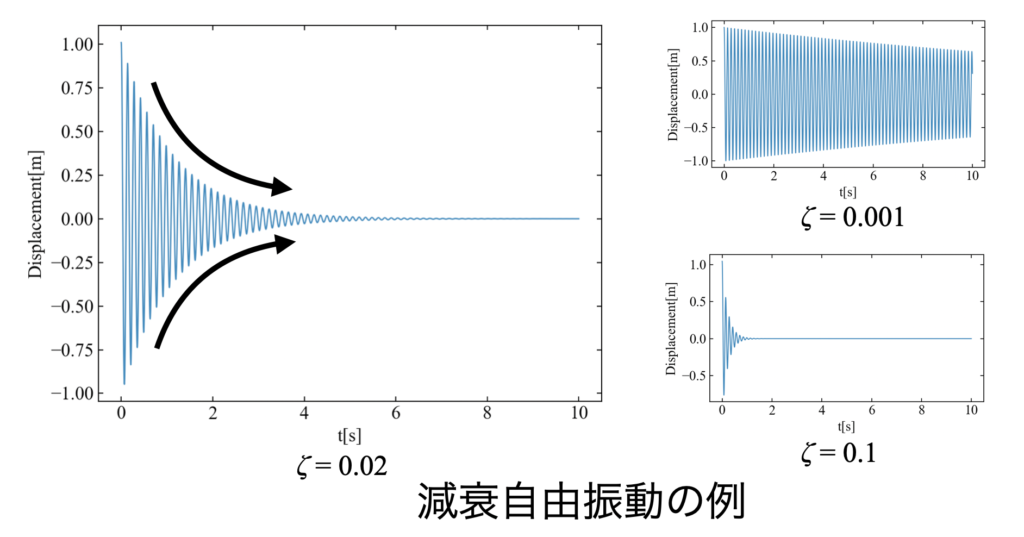
図に示すように、\(\zeta\)の数値によって振動波形の様相が変わります。\(\zeta\)は減衰率(減衰比)と呼ばれるパラメータで、大きいほど振動がはやく止まる系となります。
当ブログでは減衰自由振動のシミュレーションを「Pythonで1自由度減衰系の自由振動シミュレーション」という記事で紹介しました。運動方程式や理論値も説明していますので是非ご確認ください。
対数減衰率とは?
減衰自由振動時の各振動毎における振幅は、隣り合う山(周期\(T\)後の振幅値)が指数関数曲線に従って減少する特徴を持ちます。
そのため、振幅値の対数(デシベル変換も同義)をとることで、その減少曲線を直線にできます。
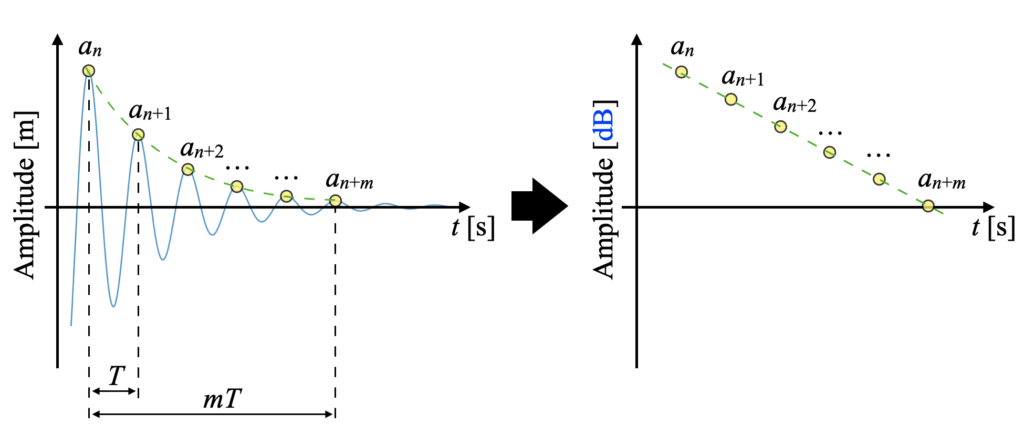
対数減衰率\(\delta\)とは、隣り合う振幅同士の比に対し自然対数をとった式(1)で示されます\(^{[1]}\)。
また1周期\(T\)の振幅比ではなく、\(m\)周期\(mT\)との振幅比を使って精度を高める式(2)の方法もあります\(^{[2]}\)。
対数減衰率と減衰比の関係
振動系は1自由度や多自由度の質点、ばね、ダンパーでモデル化することがあります。ダンパーの減衰係数と系の振動現象そのものに密接に関係する減衰比\(\zeta\)と対数減衰率\(\delta\)には式(3)の関係があります\(^{[1]}\)。
つまり対数減衰率を計測から求めることができれば、減衰比を算出でき、振動モデルのパラメータ同定が可能となります。
本記事では振動波形を計測した結果を使って自分で対数減衰率を求められるようになることを目標とします。
また、上式(1)や(2)はピーク値を手動でピックアップするかピーク検出プログラムを書く必要がありますが、今回はより連続的かつ自動的に振幅を抽出可能なヒルベルト変換を使います。
詳しくはコードを書きながら説明しますので、是非記事後半もご覧ください。
振動波形から対数減衰率と減衰比を求めるPythonコード
動作環境
この記事のコードは以下のPython環境で動作確認を行いました。
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| Scipy | 1.4.1 |
| matplotlib | 3.4.3 |
サンプルの減衰自由振動波形を作る
コピペ動作可能な全コードは最後に示しますが、まずはどのような手順でコードが書かれているのかを一つずつ説明します。
まずは自分で書いたコードを検証できるように、サンプルの減衰自由振動波形を作ってみましょう。
理論式:\(0 < \zeta < 1\)
コードを書く前に、理論式を確認します。既に当ブログでも紹介しましたが、減衰比の値により振動の様相が変化します。
\(0 < \zeta < 1\)の場合、固有角振動数\(\omega\)、減衰固有角振動数\(\omega_{d}\)を定義すると式(4)-式(9)を使って応答変位\(x\)を求めることができます\(^{[3]}\)。
理論式:\(\zeta = 1\)
同様に、式(10)の無次元化速度\(\sigma_{v0}\)を導入することで\(\zeta=1\)の場合の応答変位は式(11)で計算可能です\(^{[4]}\)。
理論式:\(\zeta > 1\)
さらに\(\zeta>1\)の場合は式(12)が応答変位の式になります\(^{[4]}\)(これはかなりややこしや)。
理論波形作成を関数にまとめたPythonコード
今回は式(9)までの内容しか検証で使いませんが、一連の式を関数damp_eq()にまとめてみました。質量\(m\)、剛性\(k\)や初期変位\(x_{0}\)、初期速度\(v_{0}\)を受け取って波形を返す仕様です。減衰係数\(c\)ではなく減衰比\(\zeta\)を与える仕様にしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt def damp_eq(m, k, zeta, x0, v0, t): ''' 減衰自由振動の理論値を計算 ''' omega = np.sqrt(k / m) sigma = omega * zeta sigma_v0 = v0 / (x0 * omega) # 減衰比の場合分け if zeta < 1: # 減衰振動 omega_d = omega * np.sqrt(1 - zeta ** 2) X = np.sqrt(x0 ** 2 + ((v0 + sigma * x0) / omega_d)) phi = np.arctan2((v0 + sigma * x0), (x0 * omega_d)) x = np.exp(-sigma * t) * X * np.cos(omega_d * t - phi) elif zeta == 1: # 臨界減衰 omega_d = omega x = x0 * np.exp(-omega * t) * ((sigma_v0 + 1) * omega * t + 1) else: # 過減衰 omega_d = omega x = x0 * np.exp(- zeta * omega * t) * (np.cosh(omega * t * np.sqrt(zeta ** 2 - 1)) + (sigma_v0 + zeta) / (np.sqrt(zeta ** 2 + 1)) * np.sinh(omega * t * np.sqrt(zeta ** 2 - 1))) return x, omega_d if __name__ == '__main__': ''' メイン処理 ''' # サンプルの減衰振動を計算(m:質量[kg], k:ばね定数[N/m], zeta:減衰率, x0:初期変位[m], v0:初速度[m/s], dt:時間刻み[s]) m = 0.5 k = 1000 zeta = 0.02 x0 = 1 v0 = 0 dt = 0.001 t = np.arange(0, 10, dt) x, omega_d = damp_eq(m, k, zeta, x0, v0, t) |
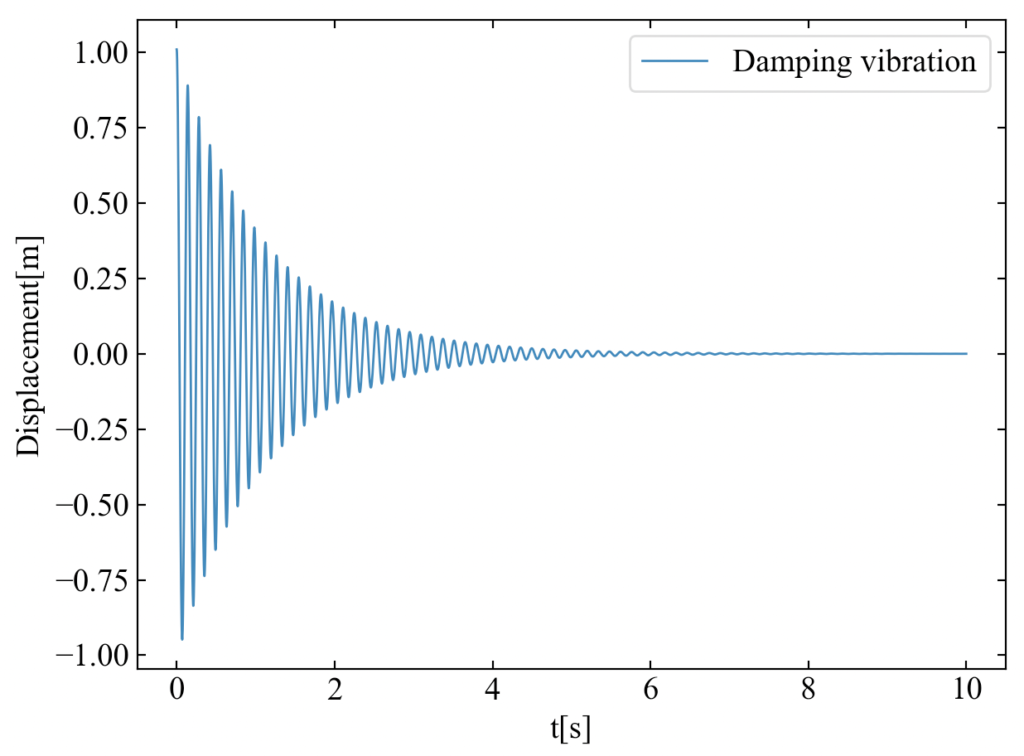
プロットを含めたコードは最後に示しますが、実行すると以下の波形を得ます。THE・減衰振動、って感じの波形にしてみました。
ヒルベルト変換で瞬時振幅を求める
次にヒルベルト変換を使って包絡線(Envelope)を求めます。包絡線を求めることで、ピーク検出アルゴリズムを使わないで自動的に減衰自由振動の振幅変化を取得できます。
ヒルベルト変換の考え方
ヒルベルト変換は波形を実部と虚部に分離して考えます。このように考えることで時間が進行していく最中の瞬時振幅、瞬時位相、瞬時周波数をそれぞれ求めることができ、時間領域の信号処理で重宝されています。
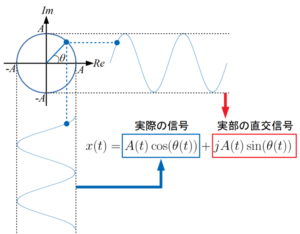
難しそうに聞こえますが、やっていることはフーリエ変換ですので、当ブログの読者であればすぐにできます。詳しく知りたい方は「Pythonでヒルベルト変換!時間波形の包絡線を求める方法」をご覧ください。
ヒルベルト変換を行うPythonコード
以下にヒルベルト変換を行うPythonコードを記載します。SciPyで1行で書けたりしますが、せっかくフルスクラッチしたので今回はこちらの方を紹介します。詳しくは参考文献\(^{[5]}\)をどうぞ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
def hilbert(yt, dt): ''' ヒルベルト変換 ''' # フーリエ変換 spectrum = fftpack.fft(yt) # 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(spectrum) / 2)) spectrum[int(len(spectrum) / 2):len(spectrum)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する spectrum *= 2 # 実部と虚部から瞬時振幅と瞬時位相を計算する zt = fftpack.ifft(spectrum) re = zt.real im = zt.imag # 瞬時振幅 instantaneous_amp = np.sqrt(re ** 2 + im ** 2) # 瞬時位相とアンラップ処理 instantaneous_phase = np.arctan2(im, re) instantaneous_phase = np.unwrap(instantaneous_phase) # 瞬時周波数(位相角の微分と時間刻み影響を考慮) instantaneous_frequency = ((1 / dt) / (2 * np.pi)) * np.gradient(instantaneous_phase) return instantaneous_amp |
このコードを実行することで包絡線(瞬時振幅)を得ます。これを元の波形と重ね描きすることでしっかりと包絡線になっていることがわかります。ただ、波形の両端部が跳ねているという点も確認できます。
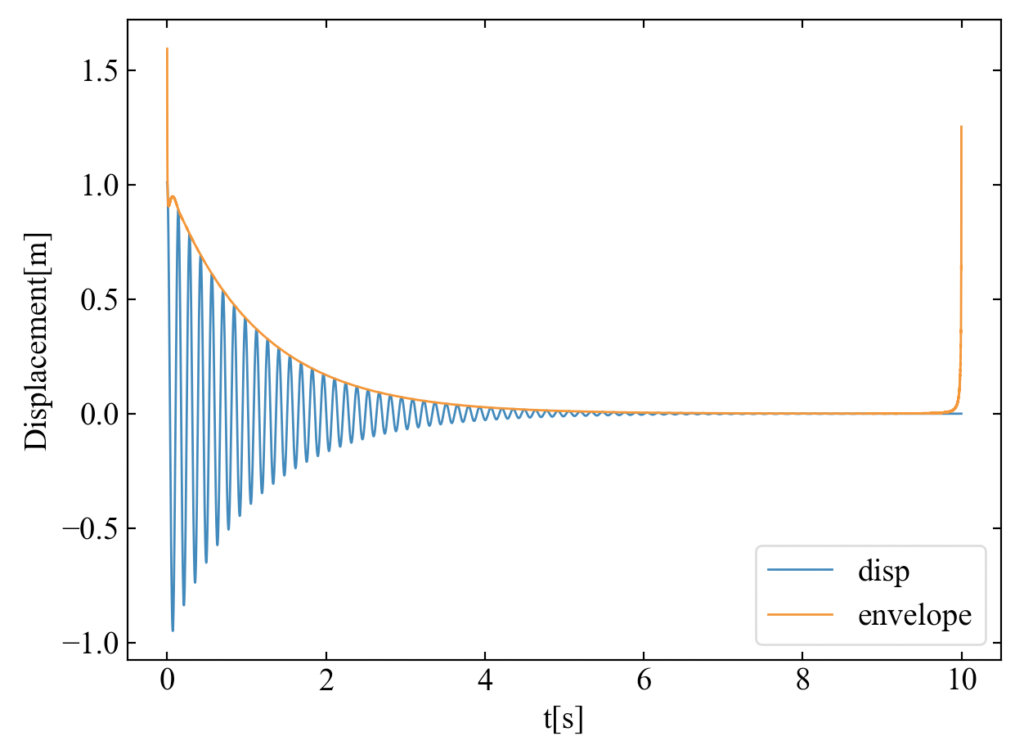
解析範囲を自動調整する
そのままカーブフィットすると精度が落ちる
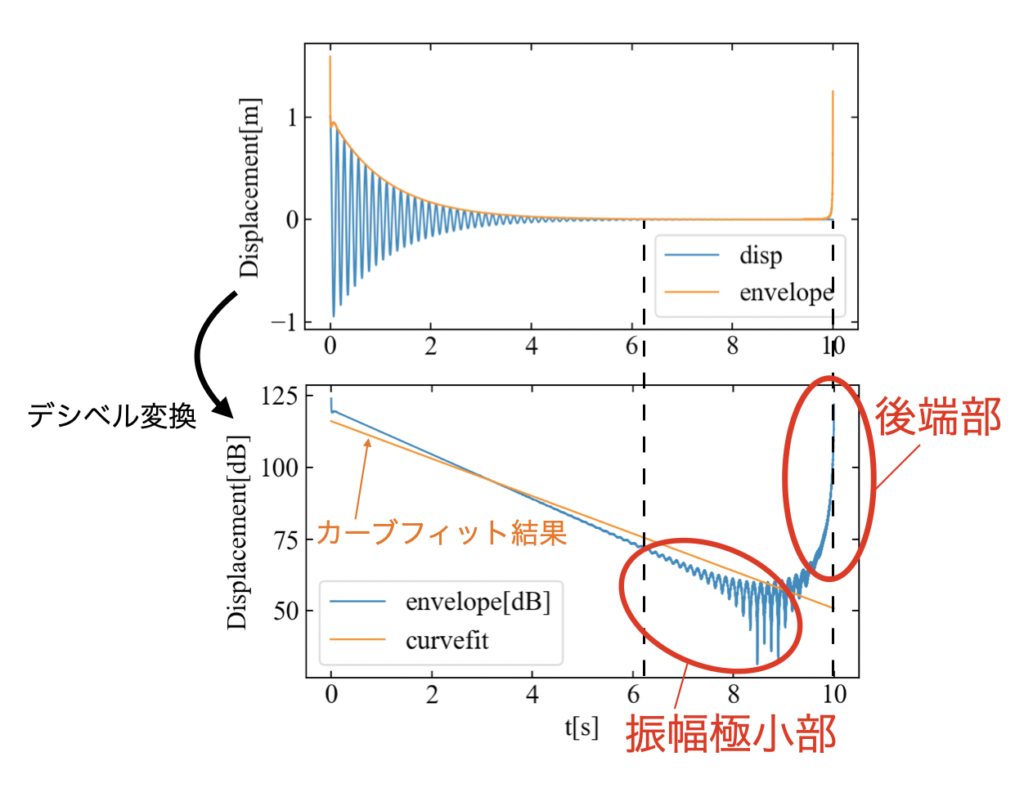
瞬時振幅が求められたので、あとは直線近似(カーブフィット)するだけと思いきや、素直にヒルベルト変換した結果を使って対数減衰率を算出しようとすると精度が悪くなっていることに気づきます。
これは図解すると一目瞭然であり、瞬時振幅の計算時にできる後端部の跳ね上がりや、ほぼ振動しなくなった振幅極小部分で対数振幅が振動することに起因します。
これは意外とやっかいで、系の固有振動数や最大振幅値、データ長にも依存します。
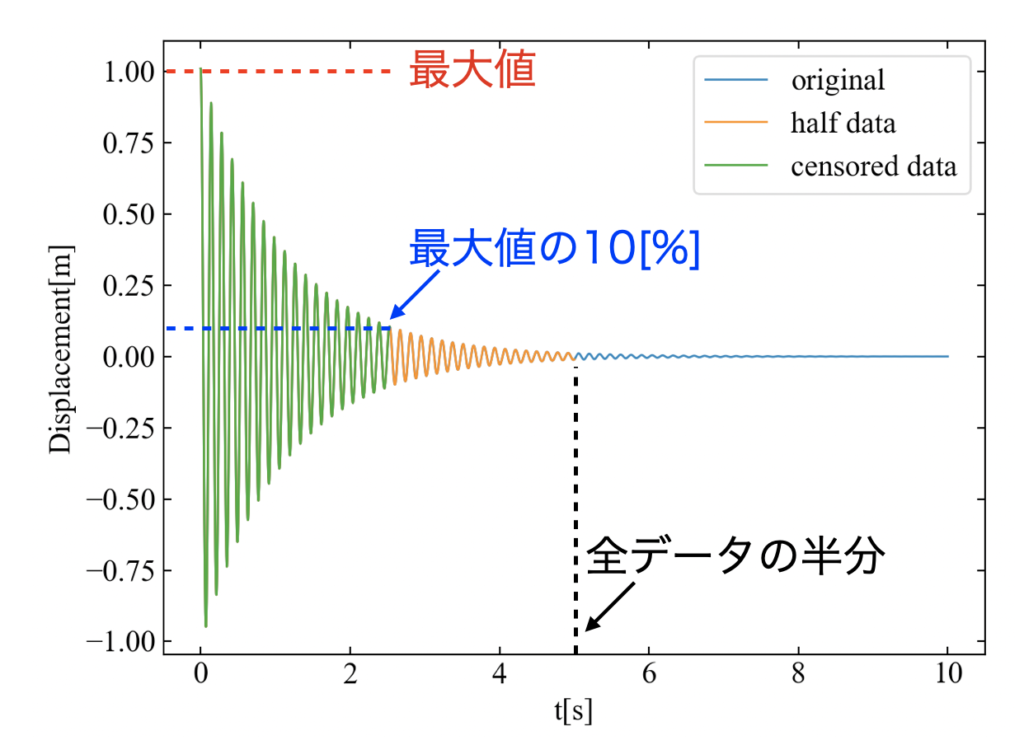
そのため元波形を使って事前に「安定して減衰振動している範囲」を自動抽出する関数を作って実行します。
今回はstable_check()という関数を作り、まずデータを半分捨てます(ここはちょっと改良の余地あり?)。次に最大振幅の10[%]以上の振幅を持つ成分のみを残すことで、対数変換後の精度悪化要因を排除します。
データの全範囲で最大振幅の10[%]に到達しない場合はデータ長の半分までが安定した振動をしていると判断されます。
解析範囲を自動調整するPythonコード
以下の関数がデータ範囲自動調整コードです。np.whereを使うことでindex探査しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def stable_check(t, y, i_amp, rate): ''' 安定して減衰振動している範囲を抽出する ''' # データの後半を切り捨て(包絡線の端部は瞬時振幅が高くなってしまうため) t_half = t[0:int(len(t) / 2)] y_half = y[0:int(len(y) / 2)] # 最大値に対するrate割合を超える振幅成分のみ抽出する peak = np.max(np.abs(y_half)) threshold = peak * rate index_max = np.max(np.where(np.abs(y_half) > threshold)) # 安定して減衰振動している範囲を抽出 t_censored = t_half[0:index_max] y_censored = y_half[0:index_max] i_amp = i_amp[0:index_max] return t_censored, i_amp |
対数減衰率と減衰比を計算する
振幅をデシベルに変換する
あとは式に沿って計算を進めるだけです。まずは応答変位(ここは加速度や速度でもOK)振幅\(x\)を式(13)でデシベル変換します。デシベル基準値\(\mathrm{dBref}\)は任意値でも問題ありません。
カーブフィットする
自動範囲調節された瞬時振幅に対してカーブフィットすると、下図になります。
計算にはこの傾き情報を使います。カーブフィットの方法は「Pythonでカーブフィット!最小二乗法で直線近似する方法」\(^{[6]}\)をご覧ください。
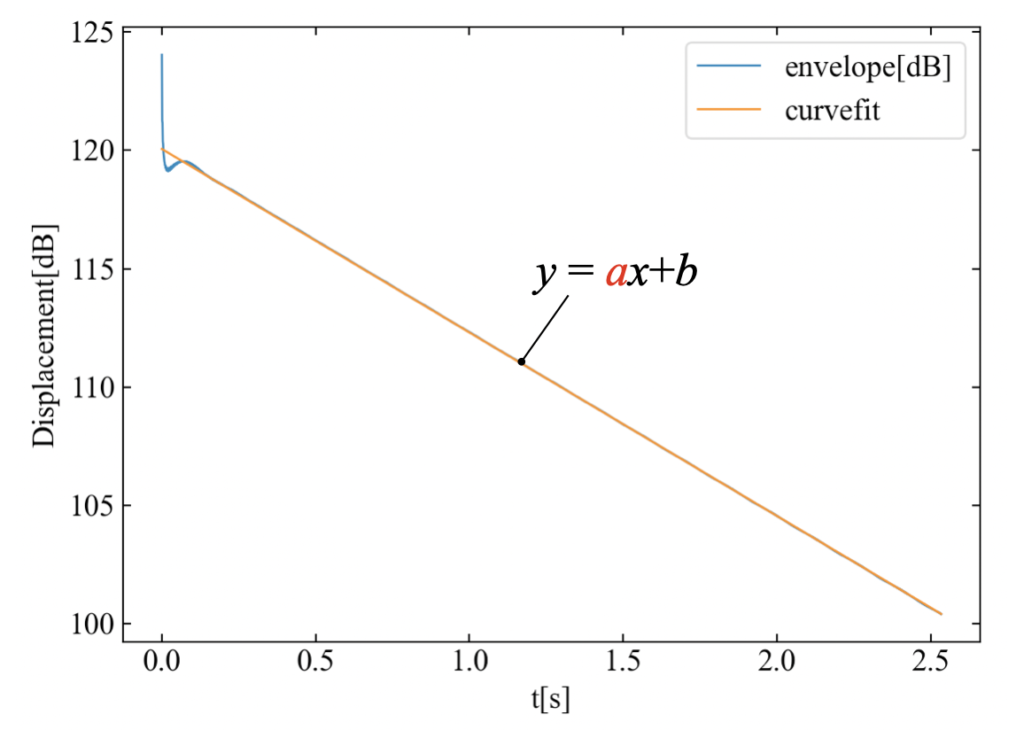
前端部も振幅が跳ねていますので、この部分を考慮して解析範囲を調整できればもう少し精度が上がりそうです。しかし実際はそれほど結果に影響していないようです。
対数減衰率と減衰比を計算する
減衰固有振動数\(f_{d}\)を式(14)、カーブフィットした結果の傾きを\(a\)とすると、式(15)で対数減衰率\(\delta\)を求めることが可能です\(^{[2]}\)。ここまで求まれば式(3)で減衰比\(\zeta\)も計算できます。
対数減衰率と減衰比を求めるPythonコード
calc_damping_factor()関数に対数減衰率と減衰比を計算する一連のコードをまとめました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def calc_damping_factor(t, y, omega_d): ''' 対数減衰率と減衰比を計算(ヒルベルト変換結果を用いて)''' # デシベル変換(dBrefは何でも良い) y_dB = 20 * np.log10(y / 1e-6) # カーブフィット coefficients = np.polyfit(t, y_dB, 1) damp_curve = coefficients[0] * t + coefficients[1] plot([t, t], [y_dB, damp_curve], ['envelope[dB]', 'curvefit'], 't[s]', 'Displacement[dB]') # 対数減衰率deltaと減衰比zetaを計算 a = -coefficients[0] fd = omega_d * (1 / (2 * np.pi)) delta = (a / fd) * (np.log(10) / 20) zeta = delta / (2 * np.pi) return zeta |
全コード(コピペ可:プロット含む)
以下に全コードを示します。このコードにはmatplotlibによるプロットを含みます。実行すると順次グラフが出てきます。一つずつ×印でウィンドウを消すと次の処理に進みます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt def damp_eq(m, k, zeta, x0, v0, t): ''' 減衰自由振動の理論値を計算 ''' omega = np.sqrt(k / m) sigma = omega * zeta sigma_v0 = v0 / (x0 * omega) # 減衰比の場合分け if zeta < 1: # 減衰振動 omega_d = omega * np.sqrt(1 - zeta ** 2) X = np.sqrt(x0 ** 2 + ((v0 + sigma * x0) / omega_d)) phi = np.arctan2((v0 + sigma * x0), (x0 * omega_d)) x = np.exp(-sigma * t) * X * np.cos(omega_d * t - phi) elif zeta == 1: # 臨界減衰 omega_d = omega x = x0 * np.exp(-omega * t) * ((sigma_v0 + 1) * omega * t + 1) else: # 過減衰 omega_d = omega x = x0 * np.exp(- zeta * omega * t) * (np.cosh(omega * t * np.sqrt(zeta ** 2 - 1)) + (sigma_v0 + zeta) / (np.sqrt(zeta ** 2 + 1)) * np.sinh(omega * t * np.sqrt(zeta ** 2 - 1))) return x, omega_d def hilbert(yt, dt): ''' ヒルベルト変換 ''' # フーリエ変換 spectrum = fftpack.fft(yt) # 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(spectrum) / 2)) spectrum[int(len(spectrum) / 2):len(spectrum)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する spectrum *= 2 # 実部と虚部から瞬時振幅と瞬時位相を計算する zt = fftpack.ifft(spectrum) re = zt.real im = zt.imag # 瞬時振幅 instantaneous_amp = np.sqrt(re ** 2 + im ** 2) # 瞬時位相とアンラップ処理 instantaneous_phase = np.arctan2(im, re) instantaneous_phase = np.unwrap(instantaneous_phase) # 瞬時周波数(位相角の微分と時間刻み影響を考慮) instantaneous_frequency = ((1 / dt) / (2 * np.pi)) * np.gradient(instantaneous_phase) return instantaneous_amp def stable_check(t, y, i_amp, rate): ''' 安定して減衰振動している範囲を抽出する ''' # データの後半を切り捨て(包絡線の端部は瞬時振幅が高くなってしまうため) t_half = t[0:int(len(t) / 2)] y_half = y[0:int(len(y) / 2)] # 最大値に対するrate割合を超える振幅成分のみ抽出する peak = np.max(np.abs(y_half)) threshold = peak * rate index_max = np.max(np.where(np.abs(y_half) > threshold)) # 安定して減衰振動している範囲を抽出 t_censored = t_half[0:index_max] y_censored = y_half[0:index_max] i_amp = i_amp[0:index_max] plot([t, t_half, t_censored], [y, y_half, y_censored], ['original', 'half data', 'censored data'], 't[s]', 'Displacement[m]') return t_censored, i_amp def calc_damping_factor(t, y, omega_d): ''' 対数減衰率と減衰比を計算(ヒルベルト変換結果を用いて)''' # デシベル変換(dBrefは何でも良い) y_dB = 20 * np.log10(y / 1e-6) # カーブフィット coefficients = np.polyfit(t, y_dB, 1) damp_curve = coefficients[0] * t + coefficients[1] plot([t, t], [y_dB, damp_curve], ['envelope[dB]', 'curvefit'], 't[s]', 'Displacement[dB]') # 対数減衰率deltaと減衰比zetaを計算 a = -coefficients[0] fd = omega_d * (1 / (2 * np.pi)) delta = (a / fd) * (np.log(10) / 20) zeta = delta / (2 * np.pi) return zeta def plot(t, x, label, xlabel, ylabel): ''' シミュレーション結果をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel(xlabel) ax1.set_ylabel(ylabel) # スケールを設定する。 #ax1.set_xlim(0, 4) # プロットを行う。 for i in range(len(x)): ax1.plot(t[i], x[i], label=label[i], lw=1) ax1.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() return if __name__ == '__main__': ''' メイン処理 ''' # サンプルの減衰振動を計算(m:質量[kg], k:ばね定数[N/m], zeta:減衰率, x0:初期変位[m], v0:初速度[m/s], dt:時間刻み[s]) m = 0.5 k = 1000 zeta = 0.02 x0 = 1 v0 = 0 dt = 0.001 t = np.arange(0, 10, dt) x, omega_d = damp_eq(m, k, zeta, x0, v0, t) plot([t], [x], ['Damping vibration'], 't[s]', 'Displacement[m]') # ヒルベルト変換から包絡線(瞬時振幅)を計算 i_amp = hilbert(x, dt) plot([t, t], [x, i_amp], ['disp', 'envelope'], 't[s]', 'Displacement[m]') # 減衰係数を計算する範囲を自動抽出(rate:データを抽出する最大振幅に対する割合) t, i_amp = stable_check(t, x, i_amp, 0.1) # 減衰係数を計算 zeta_measure = calc_damping_factor(t, i_amp, omega_d) # 理論値との精度を確認 print('Theoretical zeta =', zeta) print('Measured zeta =', zeta_measure) print('Accuracy =', zeta_measure / zeta) |
最後に理論値として与えた減衰比と測定によって求められた減衰比の比較結果がコンソールに出力されます。Accuracyは1が完全一致なので、今回の結果は0.2[%]程度のずれと読み取れます。
|
1 2 3 |
Theoretical zeta = 0.02 Measured zeta = 0.019964782847878126 Accuracy = 0.9982391423939063 |
精度検証:減衰比を振って理論値と比較する
最後に上記全コードを使って、減衰比を色々と振って理論値と比較してみましょう。手動でやるのはすごく面倒なので、上のコードのメイン部をforループで囲い、パラメータをリスト形式で与える等小変更して回してみます。
以下が検証結果です。理論波形で与えた減衰率と測定された減衰率は、\(\zeta<0.2\)あたりまでは2[%]程度のずれであるのに対し、\(\zeta>0.2\)は精度が落ちていることを確認しました。
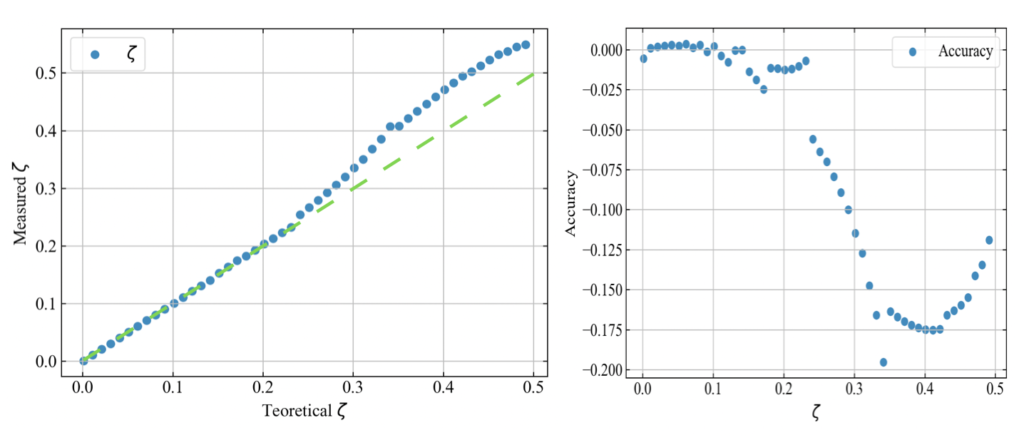
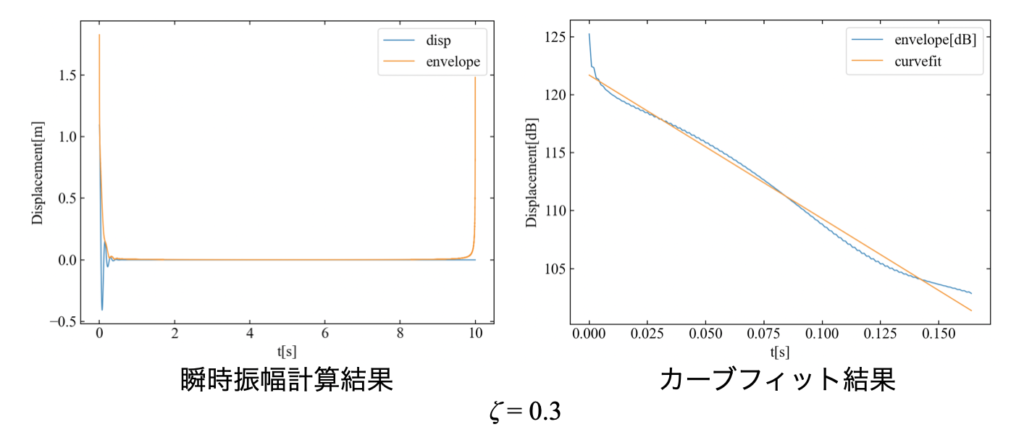
以下は精度の悪かった\(\zeta=0.3\)の場合の計算結果ですが、減衰比が高くなると安定して減衰振動する山の数がそもそも少なくなっています。
簡単な構造物でハンマリング試験を行うと金属材料で\(\zeta\)≒0.01程度、ゴム材料で\(\zeta\)≒0.1程度の印象です。実用には問題ないと思いますが、さらなる精度UPにはヒルベルト変換を用いた方法以外を考える必要がありそうです(理論式はわかっているので、時間波形に直接フィッティングさせる等)。
参考までに、精度検証に使用した全コードも記載しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt def damp_eq(m, k, zeta, x0, v0, t): ''' 減衰自由振動の理論値を計算 ''' omega = np.sqrt(k / m) sigma = omega * zeta sigma_v0 = v0 / (x0 * omega) # 減衰比の場合分け if zeta < 1: # 減衰振動 omega_d = omega * np.sqrt(1 - zeta ** 2) X = np.sqrt(x0 ** 2 + ((v0 + sigma * x0) / omega_d)) phi = np.arctan2((v0 + sigma * x0), (x0 * omega_d)) x = np.exp(-sigma * t) * X * np.cos(omega_d * t - phi) elif zeta == 1: # 臨界減衰 omega_d = omega x = x0 * np.exp(-omega * t) * ((sigma_v0 + 1) * omega * t + 1) else: # 過減衰 omega_d = omega x = x0 * np.exp(- zeta * omega * t) * (np.cosh(omega * t * np.sqrt(zeta ** 2 - 1)) + (sigma_v0 + zeta) / (np.sqrt(zeta ** 2 + 1)) * np.sinh(omega * t * np.sqrt(zeta ** 2 - 1))) return x, omega_d def hilbert(yt, dt): ''' ヒルベルト変換 ''' # フーリエ変換 spectrum = fftpack.fft(yt) # 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(spectrum) / 2)) spectrum[int(len(spectrum) / 2):len(spectrum)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する spectrum *= 2 # 実部と虚部から瞬時振幅と瞬時位相を計算する zt = fftpack.ifft(spectrum) re = zt.real im = zt.imag # 瞬時振幅 instantaneous_amp = np.sqrt(re ** 2 + im ** 2) # 瞬時位相とアンラップ処理 instantaneous_phase = np.arctan2(im, re) instantaneous_phase = np.unwrap(instantaneous_phase) # 瞬時周波数(位相角の微分と時間刻み影響を考慮) instantaneous_frequency = ((1 / dt) / (2 * np.pi)) * np.gradient(instantaneous_phase) return instantaneous_amp def stable_check(t, y, i_amp, rate): ''' 安定して減衰振動している範囲を抽出する ''' # データの後半を切り捨て(包絡線の端部は瞬時振幅が高くなってしまうため) t_half = t[0:int(len(t) / 2)] y_half = y[0:int(len(y) / 2)] # 最大値に対するrate割合を超える振幅成分のみ抽出する peak = np.max(np.abs(y_half)) threshold = peak * rate index_max = np.max(np.where(np.abs(y_half) > threshold)) # 安定して減衰振動している範囲を抽出 t_censored = t_half[0:index_max] y_censored = y_half[0:index_max] i_amp = i_amp[0:index_max] #plot([t, t_half, t_censored], [y, y_half, y_censored], ['original', 'half data', 'censored data'], 't[s]', 'Displacement[m]') return t_censored, i_amp def calc_damping_factor(t, y, omega_d): ''' 対数減衰率を計算(ヒルベルト変換結果を用いて)''' # デシベル変換(dBrefは何でも良い) y_dB = 20 * np.log10(y / 1e-6) # カーブフィット coefficients = np.polyfit(t, y_dB, 1) damp_curve = coefficients[0] * t + coefficients[1] #plot([t, t], [y_dB, damp_curve], ['envelope[dB]', 'curvefit'], 't[s]', 'Displacement[dB]') # 減衰係数zetaを計算 dX = 1 dY = -coefficients[0] fd = omega_d * (1 / (2 * np.pi)) p = dX * fd delta = (1 / p) * np.abs(dY / dX) * (np.log(10) / 20) zeta = delta / (2 * np.pi) return zeta def plot(t, x, label, xlabel, ylabel): ''' シミュレーション結果をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel(xlabel) ax1.set_ylabel(ylabel) # スケールを設定する。 #ax1.set_xlim(0, 4) # プロットを行う。 for i in range(len(x)): ax1.scatter(t[i], x[i], label=label[i], lw=1) ax1.grid() ax1.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() return if __name__ == '__main__': ''' メイン処理 ''' zetas = np.arange(0.001, 0.5, 0.01) zetas_measured = [] accuracies = [] for i in range(len(zetas)): # サンプルの減衰振動を計算(m:質量[kg], k:ばね定数[N/m], zeta:減衰率, x0:初期変位[m], v0:初速度[m/s], dt:時間刻み[s]) m = 0.5 k = 1000 zeta = zetas[i] x0 = 1 v0 = 0 dt = 0.001 t = np.arange(0, 10, dt) x, omega_d = damp_eq(m, k, zeta, x0, v0, t) # ヒルベルト変換から包絡線(瞬時振幅)を計算 i_amp = hilbert(x, dt) #plot([t, t], [x, i_amp], ['disp', 'envelope'], 't[s]', 'Displacement[m]') # 減衰係数を計算する範囲を自動抽出(rate:データを抽出する最大振幅に対する割合) t, i_amp = stable_check(t, x, i_amp, 0.1) # 減衰係数を計算 zeta_measure = calc_damping_factor(t, i_amp, omega_d) zetas_measured.append(zeta_measure) # 精度を計算 accuracy = 1 - (zeta_measure / zeta) accuracies.append(accuracy) # 理論値との精度を確認 print('Theoretical zeta =', zeta) print('Measured zeta =', zeta_measure) print('Accuracy =', accuracy) plot([zetas], [zetas_measured], ['$\zeta$'], 'Teoretical $\zeta$', 'Measured $\zeta$') plot([zetas], [accuracies], ['Accuracy'], '$\zeta$', 'Accuracy') |
まとめ
本記事では減衰自由振動の対数減衰率と減衰比をPythonで測定する方法を学びました。
式自体は比較的有名ですが、実際に測定しようと思うとデータ処理を色々やらないと精度が著しく悪化するということもわかりました。
今回は理想波形における測定を行いましたが、次回は実際の音振波形に対して適用する方法を検討します。
おそらくフィルタ処理等を色々しないと実問題には適用できないと考えられるので、この記事は第1歩といったところ。
参考文献
[1]:金子成彦, 大熊政明, 機械力学ハンドブック, 朝倉書店, 2015(初版第1刷), pp87 [2]: 小野測器, 減衰をあらわす係数の意味と求め方 [3]:Pythonで1自由度減衰系の自由振動シミュレーション [4]:Wikipedia, 減衰振動 [5]:Pythonでヒルベルト変換!時間波形の包絡線を求める方法 [6]:Pythonでカーブフィット!最小二乗法で直線近似する方法これで減衰特性を測定できるようになりました!また、ヒルベルト変換も十分使いこなせるようになった気がします!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!