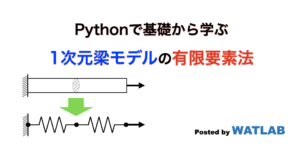
有限要素法は一般的に商用ソフトやオープンソースのライブラリを活用して「使う」ことが多いものですが、理解するためには自分でプログラミングするのが一番です。ここでは手計算でもできるレベルの問題をPythonによる有限要素法コードで解くことで、計算の流れを把握することを目指します。
続きを読むシミュレーション
WindowsのWSL2でPython3/GetFEMを使ってみた
計算力学技術者試験の勉強のため、Pythonで使える有限要素法ライブラリGetFEMを使ってみました。GetFEMは通常Linux環境が必要ですが、WindowsでもWSLを使えばLinux環境を手にいれることができます。ここではWindows機でGetFEMを使う時のメモを紹介します。
続きを読む回転機の振動シミュレーションで回転パルスを設定してみた
先日の記事で回転機のアンバランス振動シミュレーションをPythonで行いました。振れ回り振動と参考書の対応がとれたので、次はより詳細な分析を行うために回転パルス(基準信号)をシミュレーションで設定してみます。ここではPythonのodeintで基準パルスを設定しながらアンバランス振動のシミュレーションを行う方法を紹介します。
続きを読む回転機のアンバランス振動をシミュレートするPythonコード
工業製品である回転機はアンバランスを修正することで精密な回転を実現しています。しかし、アンバランスを真に0にすることは難しく、不釣り合い振動の影響をシミュレーションすることは重要です。ここではPythonのscipy.odeintを使ってアンバランス振動を解析する方法を紹介します。
続きを読むPythonで多自由度振動系の過渡応答計算をする時はSciPyを使おう
このブログではしばらく自前のルンゲ・クッタ法を使って振動解析を行ってきました。しかしPythonで常微分方程式の数値計算をする時はSciPyのodeintを使った方が良いです。ここでは巨人の肩に乗るつもりでSciPy/odeintで振動問題を解くための例題を紹介します。
続きを読む振動波形のヒルベルト変換から対数減衰率を求めるPythonコード
減衰自由振動現象の重要な特性に減衰率があります。減衰特性は物性から求めることが難しいので、実際に系を振動させて測定することが一般的です。ここでは減衰自由振動の波形に対してヒルベルト変換を行い、対数減衰率を計算するPythonコードを紹介します。
続きを読むPythonで2次元拡散方程式を数値解析して定常解析と比較する
数値流体力学の学習は各要素毎に離散化手法と解析手法を学ぶことが重要です。ここでは2次元の拡散方程式の概要や離散化手法を説明し、Pythonで実装しながら学習します。結果は定常解析の結果と比較することでラプラス方程式にも触れてみます。
続きを読むPythonで2次元移流方程式を数値計算する方法
1次元移流方程式で基礎を学んだ後は2次元移流方程式を学びます。ここでは2次元移流方程式の差分化手法の例とPythonコードによるアニメーション作成までを行います。2次元の初期場を作る方法、漸化式の更新方法、結果のプロット方法について考えてみた結果を紹介します。
続きを読む2D数値計算の境界条件を画像から作るPythonコード例
2Dの流体解析をする時、計算領域内部に置いた構造物の影響を考慮したくなります。ここでは画像の輪郭から流体解析に使用できる境界条件を作る1つの例を、Pythonの流体解析コードと画像処理コードをコラボしながら考察してみたいと思います。
続きを読むPythonで2次元ラプラス方程式を数値計算する方法
時間によって変化しない定常状態を示すラプラス方程式は様々な物理現象の基礎となっています。ここではラプラス方程式の差分化から説明します。また、学習の理解を深めるために簡単な2次元のラプラス方程式をPythonを使って数値計算する方法を紹介します。
続きを読む