振動モデルを直接法の周波数応答解析で解くPythonコード

振動シミュレーションの代表的な解法の1つに周波数応答解析があります。この解析手法は時間領域ではなく周波数領域で計算をするため、一般的に計算負荷が軽いとされ実際の設計現場で重宝されています。ここではPythonで振動モデルを周波数応答解析で解く例を紹介します。

こんにちは。wat(@watlablog)です。ここではPythonで周波数応答解析による振動シミュレーションをやってみます！

目次（項目クリックでジャンプできます）

本記事の対象者

高速に振動解析をしたい人

本記事は高速に振動解析をしたい人を対象としています。振動解析には様々な種類がありますが、それぞれ一長一短があります。ここではまずはじめに代表的な解析手法である過渡応答解析と本記事で扱う周波数応答解析の違いを説明します。

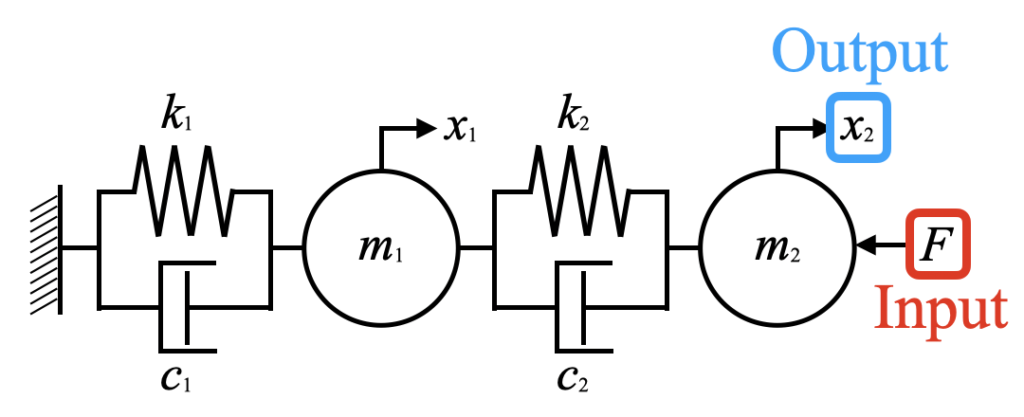
過渡応答解析と周波数応答解析の違い

当ブログでは最初に過渡応答解析(Transient Response Analysis)を扱いました。過渡応答解析は時刻暦応答解析とも呼ばれ、時間刻み毎に横軸時間で運動方程式を解析する手法です。

当ブログでは「Pythonの4次ルンゲ・クッタ法で多自由度連成振動を解く方法」や「Pythonでレイリー減衰を実装する方法！解析して効果を見てみる」という記事で主に4次のルンゲ・クッタ法を使って過渡応答解析を扱いました。

時刻暦の解析をすると、以下のようなアウトプットが得られます。

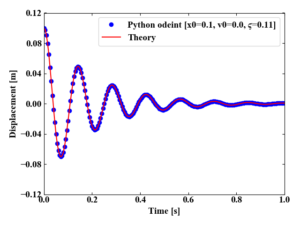
まだ過渡応答解析をやった事がない方は是非これらの記事を読んでみて下さい。

一方、周波数応答解析(Frequency Response Analysis)は、時刻暦ではなく周波数軸で運動方程式を解析する手法です。

過渡応答解析の後にフーリエ変換を行う事でも、各周波数でどのような特性になっているかといった分析をする事はできます。しかし、過渡応答解析は非線形な現象や大変形の現象を解析する目的には向いているものの、定常状態（振動が最終的に安定する状態等）を解析する事には向きません。

「Pythonの過渡応答解析で力を滑らかにかけて応答の違いを見る」という記事では、過渡応答解析で振動が安定した状態の分析を試みましたが、加振を滑らかにかけたりと工夫が色々必要でした。

そして安定するまでの時間分計算をしないとならないので、計算時間がかなりかかります。

周波数応答解析であれば、はじめから定常状態となるように運動方程式を立てるため、過渡応答解析に比べ計算時間は圧倒的に早いです。

実際の企業の設計現場ではスピードが命ですので、主に計算時間の理由で周波数応答解析がよく使われています。

周波数応答解析の解き方や実装方法を知りたい人

本ページでは周波数応答解析による運動方程式の解法を、式の導出から説明します。さらに、PythonのNumpyというライブラリを使って1からコード実装する所も紹介します。

「Pythonで多自由度系の固有値解析！固有振動数とモードを計算」でも書きましたが、会社でただブラックボックスとして計算をしているだけだと本質は理解した事になりませんが、自分で式の導出をしてからプログラムで計算を実装する事ができれば、実際に会社のソフトを使う時でも質の高い仕事ができるようになると思います。

それでは早速周波数応答解析の式から説明していきましょう！

周波数応答解析の式

直接法とモード法について

周波数応答解析には、設定したモデルをそのままフルマトリクスとして解く直接法と、固有値解析の結果を利用してモデルを縮退してさらに高速に計算しようというモード法があります。

今回は基礎を学ぶという趣旨なので、この記事では基本である直接法の説明を行います。

モード法は後で。

運動方程式を立てる

振動問題の場合、質量行列\(\mathbf{M}\)、減衰行列\(\mathbf{C}\)、剛性行列\(\mathbf{K}\)と変位ベクトル\(\mathbf{x}\)、速度ベクトル\(\mathbf{\dot{x}}\)、加速度ベクトル\(\mathbf{\ddot{x}}\)、さらに外力ベクトル\(\mathbf{f}\)を使うと、減衰強制振動の運動方程式は式(1)となります。

\[ \mathbf{M}\mathbf{\ddot{x}}+\mathbf{C}\mathbf{\dot{x}}+\mathbf{K}\mathbf{x}=\mathbf{f} \tag{1} \]

行列形式の運動方程式の立て方

ニュートンの運動方程式は1自由度の場合で立てるのは有名ですが、多自由度（質点やばねが沢山あるもの）の場合はあまり初心者向けの記事や文献を見かけませんでした（皆さん知っていて当たり前…のような感じで始まるものが多いい印象）。

当ブログは初心者向けに以下の記事で多自由度振動系の運動方程式を行列やベクトル形式で立てる方法を解説していますので、まだ自由に式を立てる事が困難な方はまずこの記事をご確認下さい。

「Pythonで計算するために多自由度振動系を行列形式にする方法」

離散の角振動数と外力を定義する

周波数応答解析は設定した周波数毎に計算を行うため、離散の周波数を考える必要があります。

周波数を角振動数\(\omega\)[rad/s]として式(2)と定義します。ここで\(n\)は整数で、この式(2)は初期角振動数\(\omega_{0}\)から\(n\omega_{0}\)までを等倍になるように角振動数の軸ができる事になります。

\[ \omega=n\omega_{0} \tag{2} \]

続いて外力ベクトルを定義します。周波数応答解析の場合、外力ベクトルは定常振動を仮定するため、明確な加振の形を最初から設定します。

振動の表現方法として、今回は指数関数\(e\)の形をとり、式(3)と定義します。この形はオイラーの定理により正弦波と余弦波で表す事ができるため、明らかに定常振動する形となります。

\(\mathbf{f}_{n}\)と外力ベクトルに\(n\)が付いているのは、各角振動数毎に外力を作るという意味程度です。

\[ \mathbf{f}=\mathbf{f}_{n} e^{i\omega t} \tag{3} \]

振動解を定義する

続いて、振動解を定義します。

1自由度の場合でやった時と同じように、変位ベクトル\(\mathbf{x}\)を1階微分、2階微分して式(1)に対応する速度ベクトルと加速度ベクトルをそれぞれ式(4)と定義します。オイラーの定理が使えるおかげで微分が楽です。

\[ \left\{\begin{matrix} \mathbf{x}&=&\mathbf{x}_{n} e^{i\omega t}\\ \mathbf{\dot{x}}&=&i\omega\mathbf{x}_{n} e^{i\omega t}\\ \mathbf{\ddot{x}}&=&-\omega^{2}\mathbf{x}_{n} e^{i\omega t} \end{matrix}\right. \tag{4} \]

周波数毎に解が出る式に変形する

後は式(1)に式(3)と式(4)を代入し、式(5)に示す通り\(n\)番目の変位ベクトル\(\mathbf{x}_{n}\)の式に変形する事で、周波数応答解析の基礎式が出来上がります。

\[ \begin{eqnarray} \mathbf{M}(\omega^{2}\mathbf{x}_{n} e^{i\omega t})+\mathbf{C}(i\omega\mathbf{x}_{n} e^{i\omega t})+\mathbf{K}(\mathbf{x}_{n} e^{i\omega t})&=&\mathbf{f}_{n} e^{i\omega t}\\ \left [ - \omega^{2}\mathbf{M}+i\omega\mathbf{C}+\mathbf{K} \right ]\mathbf{x}_{n} &=& \mathbf{f}_{n}\\ \mathbf{x}_{n} &=& \left [ - \omega^{2}\mathbf{M}+i\omega\mathbf{C}+\mathbf{K} \right ]^{-1}\mathbf{f}_{n} \tag{5} \end{eqnarray} \]

指数関数部を全部消す事ができ、さらに変位ベクトル\(\mathbf{x}_{n}\)でくくる事で、行列計算部分がひとまとめにできるため、最後に逆行列計算を行う事で解を求める事が可能な式になります。

それではここからPythonで実装する方法を検討していきましょう！

Pythonで直接法の周波数応答解析を計算するコード

動作環境

このページに記載のコードは以下のPC環境で検証しました。参考までに。

PC

Windows	OS	Windows10 64bit
	CPU	2.4[GHz]
	メモリ	4[GB]

Mac	OS	macOS Catalina 10.15.7
	CPU	1.4[GHz]
	メモリ	8[GB]

Python環境

Python環境は以下です。外部ライブラリはNumpyと結果可視化用にmatplotlibを使っています。

Python	Python 3.7.7
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.19.0
matplotlib	3.2.2

モデルを定義する

全コードを紹介する前に、コードのキーポイントとなる部分を簡単に説明します。

まず初めに、振動モデルを定義します。モデル定義と言っても式(5)の質量行列、剛性行列、減衰行列を定義するという意味になります。

質量行列と剛性行列（sympy使って簡単に作る事もできる）

基本は「Pythonで計算するために多自由度振動系を行列形式にする方法」で自力で各質点周りの力関係を洗い出していく必要がありますが、洗い出した後は数式をそのままシンボリックに計算する事が可能なPythonのsympyというライブラリで若干楽をする事もできます。

僕のようにしょっちゅう式変形で凡ミスを繰り返す人は自動で式変形をしてくれるsympyに全てを委ねて楽をしましょう（こうして計算能力がさらに退化していくと思いますが）。悪魔の記事は以下です。

「Python/SymPyで連立運動方程式の剛性行列を自動生成する」

※上記の記事で生成した剛性行列はそのまま今回の変数定義に使用可能です。

とは言え、まずは簡単な2自由度振動系で周波数応答解析のコード検証をします。

今回は以下の質量行列と剛性行列を定義します。

# シミュレーションモデル
def model():
    # 質量・減衰・剛性の集中定数を設定する
    m1 = 0.5
    m2 = 0.5
    k1 = 30000
    k2 = 20000

    # 質量マトリクスと剛性マトリクスを作成
    M = np.array([[m1, 0],
                  [0, m2]])
    K = np.array([[k1 + k2, -k2],
                  [-k2, k2]])
    return M, K

# シミュレーションモデル

def model():

# 質量・減衰・剛性の集中定数を設定する

m1 = 0.5

m2 = 0.5

k1 = 30000

k2 = 20000

# 質量マトリクスと剛性マトリクスを作成

M = np.array([[m1, 0],

[0, m2]])

K = np.array([[k1 + k2, -k2],

[-k2, k2]])

return M, K

レイリー減衰を定義する

直接法の周波数応答解析では減衰行列をレイリー減衰で設定する事が一般的かも知れません。

レイリー減衰については以下の記事で詳細を説明しています。数値計算上の仮想的な減衰ですが、固有値をベースに減衰比を周波数軸で設定する事ができるため大変重宝されます。是非こちらの記事もご確認下さい。

「Pythonでレイリー減衰を実装する方法！解析して効果を見てみる」

本記事では以下の関数でレイリー減衰を設定します。先ほど定義した質量行列と剛性行列を使って計算を行います。

# Rayleigh dampingのパラメータを決定して減衰マトリクスを生成する関数
def generate_rayleigh_damping(f1, f2, zeta1, zeta2, M, K):
    # 指定周波数を角振動数に変換
    w1 = 2 * np.pi * f1
    w2 = 2 * np.pi * f2
    
    # alphaとbetaを使って減衰行列を計算
    alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2)
    beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2)
    C = np.array(alpha * M + beta * K)
    
    return C

# Rayleigh dampingのパラメータを決定して減衰マトリクスを生成する関数

def generate_rayleigh_damping(f1, f2, zeta1, zeta2, M, K):

# 指定周波数を角振動数に変換

w1 = 2 * np.pi * f1

w2 = 2 * np.pi * f2

# alphaとbetaを使って減衰行列を計算

alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2)

beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2)

C = np.array(alpha * M + beta * K)

return C

周波数応答解析の関数

関数全体

今回作成した周波数応答解析の関数を以下に示します。この後に詳細を説明しますが、引数として、振動モデルで必要なMCK行列、解析範囲と周波数刻みを指定するfreq_l, freq_u, step、加振点の節点番号、応答点の節点番号を渡して動作させます。

# 周波数応答解析を計算する関数
def frequency_response_analysis(M, K, C, freq_l, freq_u, step, exc_node, res_node):
    steps = 2 * np.pi * np.arange(freq_l, freq_u, step)                 # 角振動数軸
    excitation = np.ones_like(steps)                                    # 加振力[N]の周波数波形
    n_dofs = len(M)                                                     # 自由度の総数
    F = np.zeros((len(steps), n_dofs))                                  # 周波数毎の外力ベクトルを初期化

    # 角振動数分解能毎に計算するループ
    X = []
    for i in range(len(steps)):
        F[i][exc_node] = excitation[i]                                  # 外力ベクトルの更新
        matrix = (-steps[i] ** 2) * M + (1j * steps[i] * C) + K         # 逆行列にする前の行列を計算しておく
        inv_matrix = np.linalg.inv(matrix)                              # 逆行列計算
        xn = np.dot(inv_matrix, F[i])[res_node]                         # 方程式を解き、複素変位ベクトルを求める
        xn = np.sqrt(xn.real ** 2 + xn.imag ** 2)                       # 振幅成分を計算する
        X.append(xn)
    return steps, X

# 周波数応答解析を計算する関数

def frequency_response_analysis(M, K, C, freq_l, freq_u, step, exc_node, res_node):

steps = 2 * np.pi * np.arange(freq_l, freq_u, step) # 角振動数軸

excitation = np.ones_like(steps) # 加振力[N]の周波数波形

n_dofs = len(M) # 自由度の総数

F = np.zeros((len(steps), n_dofs)) # 周波数毎の外力ベクトルを初期化

# 角振動数分解能毎に計算するループ

X = []

for i in range(len(steps)):

F[i][exc_node] = excitation[i] # 外力ベクトルの更新

matrix = (-steps[i] ** 2) * M + (1j * steps[i] * C) + K # 逆行列にする前の行列を計算しておく

inv_matrix = np.linalg.inv(matrix) # 逆行列計算

xn = np.dot(inv_matrix, F[i])[res_node] # 方程式を解き、複素変位ベクトルを求める

xn = np.sqrt(xn.real ** 2 + xn.imag ** 2) # 振幅成分を計算する

X.append(xn)

return steps, X

角振動数軸を作成する

この関数では指定した低域周波数freq_lと高域周波数freq_uまでステップstep毎に応答計算を行います。以下のコード部分は周波数[Hz]を角振動数[rad/s]に変換している部分ですが、方程式は角振動数で導出しているので、この変換は必須です。

steps = 2 * np.pi * np.arange(freq_l, freq_u, step)                 # 角振動数軸

1	steps = 2 * np.pi * np.arange(freq_l, freq_u, step) # 角振動数軸

加振力行列の考え方

周波数応答解析で使用する加振力は予めゼロ行列で初期化しておきます。

サイズは行数が角振動数分、列数が振動モデルの自由度分設定します。これは後ほどforループで各角振動数毎に応答を計算させる事を想定してこの行列配置にしています。

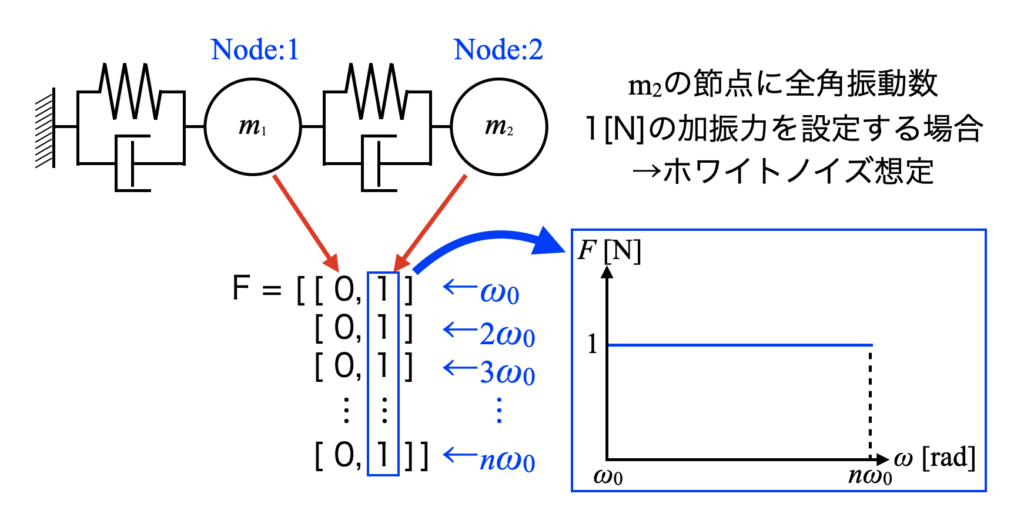
本記事のサンプルコードは2自由度振動系です。今回は拘束されていない\(m_{2}\)節点に対して全周波数1[N]の加振力を与える事とします。これはホワイトノイズ加振を想定し、振動系の固有振動数でピーク応答を得る目的です。

今回のパターンに対応する設定の図解を下図に示します。もちろん周波数毎（角振動数毎）に個別の振幅の加振力を与えても問題ありません。

やりたい事は以下ですが、実際はforループで各角振動数毎に方程式を解く所でexcitationの波形をF[i]に貼り付けています。

検証用の固有値解析関数

周波数応答解析の計算では使いませんが、コードの検証用に既に検証されている固有値解析の関数を用意しておきます。今回は2自由度振動系をホワイトノイズで加振するので、全部で2つの共振が応答のピークで確認できるはずです。

固有値解析の周波数と周波数応答解析で得られたピークを比較してコードの妥当性を確認します。

# 固有値解析を計算する関数
def eigen(M, K):
    # 質量マトリクスの逆行列を計算
    M_inv = np.linalg.inv(M)

    # 固有値と固有ベクトルを計算
    omega, v = np.linalg.eig(np.dot(M_inv, K))

    # 固有値の順番を昇順にソート
    omega_sort = np.sqrt(np.sort(omega)) #(1 / (2 * np.pi)) *

    # 固有値のソート時のインデックスを取得
    sort_index = np.argsort(omega)

    # 固有値に対応する固有ベクトルをソート
    v_sort = []
    for i in range(len(sort_index)):
        v_sort.append(v.T[sort_index[i]])
    v_sort = np.array(v_sort)
    return omega_sort, v_sort, sort_index

# 固有値解析を計算する関数

def eigen(M, K):

# 質量マトリクスの逆行列を計算

M_inv = np.linalg.inv(M)

# 固有値と固有ベクトルを計算

omega, v = np.linalg.eig(np.dot(M_inv, K))

# 固有値の順番を昇順にソート

omega_sort = np.sqrt(np.sort(omega)) #(1 / (2 * np.pi)) *

# 固有値のソート時のインデックスを取得

sort_index = np.argsort(omega)

# 固有値に対応する固有ベクトルをソート

v_sort = []

for i in range(len(sort_index)):

v_sort.append(v.T[sort_index[i]])

v_sort = np.array(v_sort)

return omega_sort, v_sort, sort_index

全コードと実行結果

以下にコピペして動作する全コードを示します。最終的には応答の変位を横軸周波数[Hz]に変換してmatplotlibにて表示させています。

import numpy as np
from matplotlib import pyplot as plt

# シミュレーションモデル
def model():
    # 質量・減衰・剛性の集中定数を設定する
    m1 = 0.5
    m2 = 0.5
    k1 = 30000
    k2 = 20000

    # 質量マトリクスと剛性マトリクスを作成
    M = np.array([[m1, 0],
                  [0, m2]])
    K = np.array([[k1 + k2, -k2],
                  [-k2, k2]])
    return M, K

# Rayleigh dampingのパラメータを決定して減衰マトリクスを生成する関数
def generate_rayleigh_damping(f1, f2, zeta1, zeta2, M, K):
    # 指定周波数を角振動数に変換
    w1 = 2 * np.pi * f1
    w2 = 2 * np.pi * f2

    # alphaとbetaを使って減衰行列を計算
    alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2)
    beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2)
    C = np.array(alpha * M + beta * K)

    return C

# 周波数応答解析を計算する関数
def frequency_response_analysis(M, K, C, freq_l, freq_u, step, exc_node, res_node):
    steps = 2 * np.pi * np.arange(freq_l, freq_u, step)                 # 角振動数軸
    excitation = np.ones_like(steps)                                    # 加振力[N]の周波数波形
    n_dofs = len(M)                                                     # 自由度の総数
    F = np.zeros((len(steps), n_dofs))                                  # 周波数毎の外力ベクトルを初期化

    # 角振動数分解能毎に計算するループ
    X = []
    for i in range(len(steps)):
        F[i][exc_node] = excitation[i]                                  # 外力ベクトルの更新
        matrix = (-steps[i] ** 2) * M + (1j * steps[i] * C) + K         # 逆行列にする前の行列を計算しておく
        inv_matrix = np.linalg.inv(matrix)                              # 逆行列計算
        xn = np.dot(inv_matrix, F[i])[res_node]                         # 方程式を解き、複素変位ベクトルを求める
        xn = np.sqrt(xn.real ** 2 + xn.imag ** 2)                       # 振幅成分を計算する
        X.append(xn)
    return steps, X

# 固有値解析を計算する関数
def eigen(M, K):
    # 質量マトリクスの逆行列を計算
    M_inv = np.linalg.inv(M)

    # 固有値と固有ベクトルを計算
    omega, v = np.linalg.eig(np.dot(M_inv, K))

    # 固有値の順番を昇順にソート
    omega_sort = np.sqrt(np.sort(omega)) #(1 / (2 * np.pi)) *

    # 固有値のソート時のインデックスを取得
    sort_index = np.argsort(omega)

    # 固有値に対応する固有ベクトルをソート
    v_sort = []
    for i in range(len(sort_index)):
        v_sort.append(v.T[sort_index[i]])
    v_sort = np.array(v_sort)
    return omega_sort, v_sort, sort_index

# モデルの質量マトリクスと剛性マトリクスを求める関数を実行
M, K = model()

# 減衰マトリクスを計算する関数を実行
C = generate_rayleigh_damping(f1=10, f2=100, zeta1=0.2, zeta2=0.1, M=M, K=K)

# 周波数応答解析を実行
freq_axis, X = frequency_response_analysis(M=M, K=K, C=C, freq_l=10, freq_u=100, step=1, exc_node=1, res_node=1)
freq_axis = freq_axis * (1 / (2 * np.pi))

# 固有値解析を実行(確認用)
omega, v, index= eigen(M, K)
print('Natural frequency[Hz]=', omega * (1 / (2 * np.pi)))

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# スケール設定
ax1.set_xscale('log')
ax1.set_yscale('log')

# 軸のラベルを設定する。
ax1.set_xlabel('Excitation frequency [Hz]')
ax1.set_ylabel('Displacement[m]')
ax1.plot(freq_axis, X, lw=1, color='red', label='Analysis Result')

# レイアウトと凡例の設定
fig.tight_layout()
plt.legend()

# グラフを表示する。
plt.show()
plt.close()

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

import numpy as np

from matplotlib import pyplot as plt

# シミュレーションモデル

def model():

# 質量・減衰・剛性の集中定数を設定する

m1 = 0.5

m2 = 0.5

k1 = 30000

k2 = 20000

# 質量マトリクスと剛性マトリクスを作成

M = np.array([[m1, 0],

[0, m2]])

K = np.array([[k1 + k2, -k2],

[-k2, k2]])

return M, K

# Rayleigh dampingのパラメータを決定して減衰マトリクスを生成する関数

def generate_rayleigh_damping(f1, f2, zeta1, zeta2, M, K):

# 指定周波数を角振動数に変換

w1 = 2 * np.pi * f1

w2 = 2 * np.pi * f2

# alphaとbetaを使って減衰行列を計算

alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2)

beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2)

C = np.array(alpha * M + beta * K)

return C

# 周波数応答解析を計算する関数

def frequency_response_analysis(M, K, C, freq_l, freq_u, step, exc_node, res_node):

steps = 2 * np.pi * np.arange(freq_l, freq_u, step) # 角振動数軸

excitation = np.ones_like(steps) # 加振力[N]の周波数波形

n_dofs = len(M) # 自由度の総数

F = np.zeros((len(steps), n_dofs)) # 周波数毎の外力ベクトルを初期化

# 角振動数分解能毎に計算するループ

X = []

for i in range(len(steps)):

F[i][exc_node] = excitation[i] # 外力ベクトルの更新

matrix = (-steps[i] ** 2) * M + (1j * steps[i] * C) + K # 逆行列にする前の行列を計算しておく

inv_matrix = np.linalg.inv(matrix) # 逆行列計算

xn = np.dot(inv_matrix, F[i])[res_node] # 方程式を解き、複素変位ベクトルを求める

xn = np.sqrt(xn.real ** 2 + xn.imag ** 2) # 振幅成分を計算する

X.append(xn)

return steps, X

# 固有値解析を計算する関数

def eigen(M, K):

# 質量マトリクスの逆行列を計算

M_inv = np.linalg.inv(M)

# 固有値と固有ベクトルを計算

omega, v = np.linalg.eig(np.dot(M_inv, K))

# 固有値の順番を昇順にソート

omega_sort = np.sqrt(np.sort(omega)) #(1 / (2 * np.pi)) *

# 固有値のソート時のインデックスを取得

sort_index = np.argsort(omega)

# 固有値に対応する固有ベクトルをソート

v_sort = []

for i in range(len(sort_index)):

v_sort.append(v.T[sort_index[i]])

v_sort = np.array(v_sort)

return omega_sort, v_sort, sort_index

# モデルの質量マトリクスと剛性マトリクスを求める関数を実行

M, K = model()

# 減衰マトリクスを計算する関数を実行

C = generate_rayleigh_damping(f1=10, f2=100, zeta1=0.2, zeta2=0.1, M=M, K=K)

# 周波数応答解析を実行

freq_axis, X = frequency_response_analysis(M=M, K=K, C=C, freq_l=10, freq_u=100, step=1, exc_node=1, res_node=1)

freq_axis = freq_axis * (1 / (2 * np.pi))

# 固有値解析を実行(確認用)

omega, v, index= eigen(M, K)

print('Natural frequency[Hz]=', omega * (1 / (2 * np.pi)))

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# スケール設定

ax1.set_xscale('log')

ax1.set_yscale('log')

# 軸のラベルを設定する。

ax1.set_xlabel('Excitation frequency [Hz]')

ax1.set_ylabel('Displacement[m]')

ax1.plot(freq_axis, X, lw=1, color='red', label='Analysis Result')

# レイアウトと凡例の設定

fig.tight_layout()

plt.legend()

# グラフを表示する。

plt.show()

plt.close()

以下が結果です。別途実行している固有値解析の結果と固有振動数が一致しました。

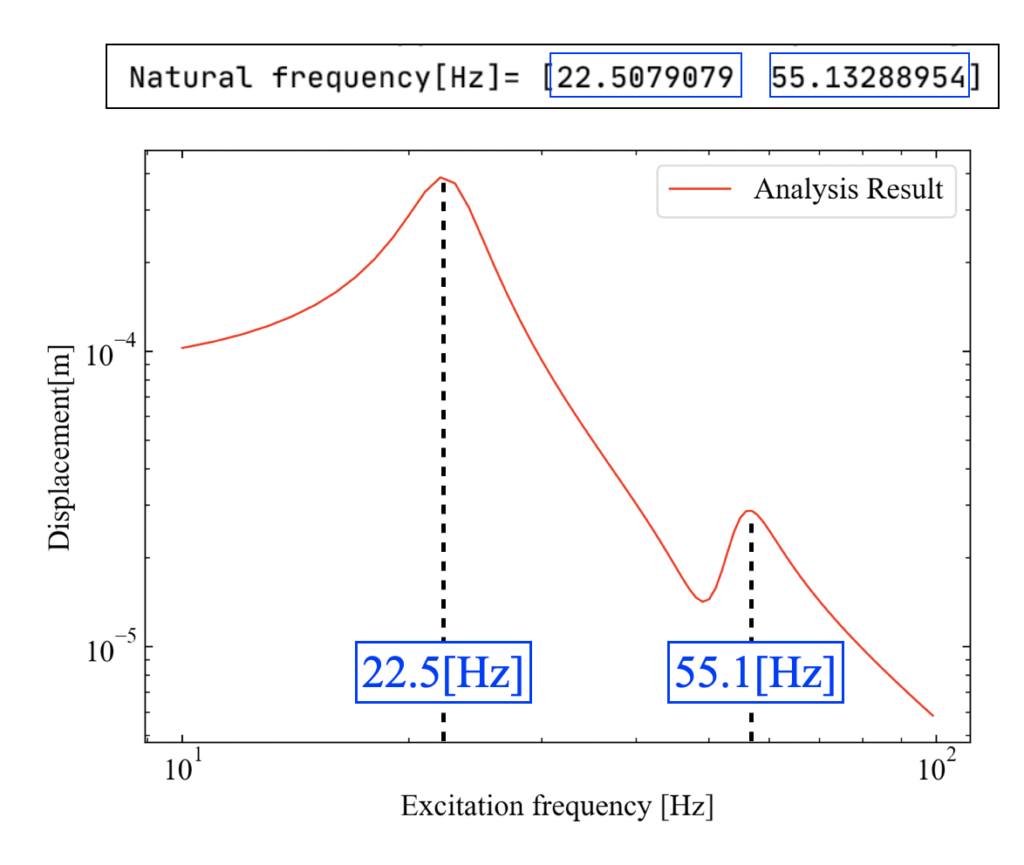
実用化のためには、加振点と応答点を複数設定できるよう(MIMO:Multi Input Multi Output)にしたり、excitation変数への加振力周波数波形の値をcsvファイルから参照するようにしたりする事が必要と思います。

まとめ

本記事では振動モデルを高速に周波数解析したい人向けに、周波数応答解析の基礎式導出方法を紹介しました。

また、Python/Numpyによる実装方法も紹介し、具体的に加振力や評価点をどのように設定すれば良いかを検討しました。

今回筆者である僕も初めて周波数応答解析のプログラムを書いてみましたが、これまでのWATLABブログでやった内容で十分理解する事ができる内容で、比較的やさしい内容だったと思います。

式ができたらそのまま行列演算を実装できるPythonの魅力も助けになっているでしょう。

周波数応答解析は今後その他解析に色々使えそうです。まずは以下の今後の展望に記載している事項を考えていますので、引き続きブログを読んで頂けたらと思います。

今後の展望（メモ）

モード法の実装

周波数応答解析は高速に計算する事が出来ますが、汎用のFEMソルバで実装されているように、モード法ができるようになる事を当面の目標とします。

線形の検討で良い場合は着目しているモードだけを表現してさらに高速に計算する事をやってみます。

信号処理技術との併用

高速な計算ができるようになったら、次は高速性を利用したソリューションを作ってみたいと思います。

まずは回転機等のように加振力が変化するモデルで周波数応答解析を多段で実施し、「Pythonで音のSTFT計算を自作！スペクトログラム表示する方法」で考案したスペクトログラムのコードで可視化する事を考えています。

周波数応答解析ができるようになりました！低自由度なモデルであれば一瞬で計算が終了します！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

本記事の対象者

高速に振動解析をしたい人

過渡応答解析と周波数応答解析の違い

周波数応答解析の解き方や実装方法を知りたい人

周波数応答解析の式

直接法とモード法について

運動方程式を立てる

行列形式の運動方程式の立て方

離散の角振動数と外力を定義する

振動解を定義する

周波数毎に解が出る式に変形する

Pythonで直接法の周波数応答解析を計算するコード

動作環境

PC

Python環境

モデルを定義する

質量行列と剛性行列（sympy使って簡単に作る事もできる）

レイリー減衰を定義する

周波数応答解析の関数

関数全体

角振動数軸を作成する

加振力行列の考え方

検証用の固有値解析関数

全コードと実行結果

まとめ

今後の展望（メモ）

モード法の実装

信号処理技術との併用

コメント

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

本記事の対象者

高速に振動解析をしたい人

過渡応答解析と周波数応答解析の違い

周波数応答解析の解き方や実装方法を知りたい人

周波数応答解析の式

直接法とモード法について

運動方程式を立てる

行列形式の運動方程式の立て方

離散の角振動数と外力を定義する

振動解を定義する

周波数毎に解が出る式に変形する

Pythonで直接法の周波数応答解析を計算するコード

動作環境

PC

Python環境

モデルを定義する

質量行列と剛性行列（sympy使って簡単に作る事もできる）

レイリー減衰を定義する

周波数応答解析の関数

関数全体

角振動数軸を作成する

加振力行列の考え方

検証用の固有値解析関数

全コードと実行結果

まとめ

今後の展望（メモ）

モード法の実装

信号処理技術との併用

SNSでもご購読できます。

コメント

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル