Pythonでレイリー減衰を実装する方法！解析して効果を見てみる

シミュレーション分野にはレイリー減衰という減衰の考え方があります。ここではPythonでレイリー減衰の曲線を書いたり、シミュレーションで使って効果を確かめたりしながら学んでいきます。

こんにちは。wat(@watlablog)です。今回はレイリー減衰って何なの？どう使うの？というのを調べてみました！

目次（項目クリックでジャンプできます）

レイリー減衰の概要

色々な減衰とレイリー減衰の特徴

「減衰」と一口に言っても様々な種類があります。

振動分野で度々出てくる、速度に比例した減衰力を発生させる粘性減衰(Viscous damping)、変位に比例する構造減衰(Structural damping)、振動モードで考えるモーダル減衰(Modal damping)…と、線形の範囲でざっと考えただけでこれだけあります。

レイリー減衰(Rayleigh damping)とは、数値解析の世界から発展した減衰の考え方であり、一般に計算を安定させる目的で使用されます。

また、レイリー減衰は固有値を基準に周波数範囲で減衰を与える事ができる特徴から、運動方程式を直接解く場合にもモーダル減衰と似たような使い方が出来る事で重宝されています。

通常の粘性減衰、構造減衰（これはヒステリシス減衰とも呼ぶ）はパラメータを設定する時に周波数軸に対する減衰度合いはなかなかイメージする事が出来ませんので、レイリー減衰はその部分に関して他の減衰と比べて異色と言えます。

但し、物理的な因果関係から成り立っている減衰では無いため、使用には注意が必要です。

レイリー減衰の構成式

レイリー減衰を説明するために、はじめに運動方程式を式(1)に示します。

\[ \mathbf{M}\mathbf{\ddot{x}}+\mathbf{C}\mathbf{\dot{x}}+\mathbf{K}\mathbf{x}=\mathbf{F} \tag{1} \]

この式の減衰マトリクス$\mathbf{C}$に対して次式の通り質量マトリクス$\mathbf{M}$と剛性マトリクス$\mathbf{K}$にそれぞれ比例定数$\alpha, \beta$をかけて加算する形にしたものがレイリー減衰(式(2))です。

\[ \mathbf{C}=\alpha \mathbf{M} + \beta \mathbf{K}\tag{2} \]

さらに、レイリー減衰では比例定数$\alpha, \beta$と減衰比$\zeta$の間に、モード毎の固有角振動数$\omega_{i}$を使って次式(3)で表します。

\[ \zeta_{i} = \frac{1}{2}(\frac{\alpha}{\omega_{i}}+\beta \omega_{i})\tag{3} \]

この式は固有角振動数が低周波数の場合は$\alpha$の方(=質量マトリクスにかかる係数)が大きくなるのに対し、高周波数の場合は$\beta$の方(=剛性マトリクスにかかる係数)が大きくなる事を意味しています。

一般にこの$\alpha, \beta$は二つの固有角振動数の範囲と対応する減衰比を決めて使用するため、以下式(4)のように二つの$\zeta$と二つの$\omega$を設定します。

\[ \begin{cases} \displaystyle　\zeta_{1} = \frac{1}{2}(\frac{\alpha}{\omega_{1}}+\beta \omega_{1})\\ \displaystyle　\zeta_{2} = \frac{1}{2}(\frac{\alpha}{\omega_{2}}+\beta \omega_{2}) \end{cases}\tag{4} \]

この2式は連立方程式として$\alpha, \beta$で解く事が可能です。
一応本ブログはPythonブログなので、PythonライブラリであるSymPyに解かせてみましょう。
コードは以下。

from sympy import*

# 変数を定義
zeta1, zeta2 = symbols('zeta1 zeta2')
omega1, omega2 = symbols('omega1 omega2')
alpha, beta = symbols('alpha beta')

# 連立方程式を定義
eq1 = Eq((1 / 2) * ((alpha / omega1) + (beta * omega1)), zeta1)
eq2 = Eq((1 / 2) * ((alpha / omega2) + (beta * omega2)), zeta2)

# 連立方程式を解いて表示
print(solve([eq1, eq2], [alpha, beta]))

from sympy import*

# 変数を定義

zeta1, zeta2 = symbols('zeta1 zeta2')

omega1, omega2 = symbols('omega1 omega2')

alpha, beta = symbols('alpha beta')

# 連立方程式を定義

eq1 = Eq((1 / 2) * ((alpha / omega1) + (beta * omega1)), zeta1)

eq2 = Eq((1 / 2) * ((alpha / omega2) + (beta * omega2)), zeta2)

# 連立方程式を解いて表示

print(solve([eq1, eq2], [alpha, beta]))

すると以下の結果を得ます。簡単に記号ベースの連立方程式を解く事が出来ました。

{beta: 2.0*(omega1*zeta1 - omega2*zeta2)/(omega1**2 - omega2**2), 
alpha: 2.0*omega1*omega2*(omega1*zeta2 - omega2*zeta1)/(omega1**2 - omega2**2)}

1 2	{beta: 2.0(omega1zeta1 - omega2zeta2)/(omega12 - omega22), alpha: 2.0omega1omega2(omega1zeta2 - omega2zeta1)/(omega12 - omega22)}

LaTeX形式で書くと式(5)。SymPyは便利ですね。

\[ \begin{cases} \displaystyle \alpha = \frac{2\omega_{1}\omega_{2}(\omega_{1}\zeta_{2}-\omega_{2}\zeta_{1})}{\omega_{1}^{2}-\omega_{2}^{2}}\\ \displaystyle \beta = \frac{2(\omega_{1}\zeta_{1}-\omega_{2}\zeta_{2})}{\omega_{1}^{2}-\omega_{2}^{2}} \end{cases}\tag{5} \]

この式を使って$\alpha, \beta$を決めれば、固有角振動数$\omega_{1}, \omega_{2}$の範囲で任意の減衰比$\zeta_{1}, \zeta_{2}$を滑らかに設定する事ができます。

ほんと？？やってみましょう！

Pythonでレイリー減衰曲線を描くコード

Advertisements

以下がPythonでレイリー減衰曲線を描画するコードです。詳細はコメントに書きましたので是非ご確認下さい。
generate_rayleigh_damping()でalphaとbetaを決定し、check_rayleigh_damping()はただグラフ表示をしているだけです。

import numpy as np
from matplotlib import pyplot as plt

# Rayleigh dampingのパラメータを決定する関数
def generate_rayleigh_damping(w1, w2, zeta1, zeta2):
    alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2)
    beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2)
    return alpha, beta

# Rayleigh dampingを描画する関数
def check_rayleigh_damping(alpha, beta, w):
    zeta = (1 / 2) * ((alpha / w) + (beta * w))
    alpha_only = (1 / 2) * alpha / w
    beta_only = (1 / 2) * beta * w

    # ここからグラフ描画-------------------------------------
    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure()

    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')

    # 軸のラベルを設定する。
    ax1.set_xlabel('$\ \omega$')
    ax1.set_ylabel('$\ \zeta$')

    # スケールの設定をする。
    ax1.set_xlim(0, 1000)

    # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
    ax1.plot(w, zeta, label='Rayleigh damping', lw=1, color='black')
    ax1.plot(w, alpha_only, label='alpha damping', lw=1, color='black', linestyle='dashed')
    ax1.plot(w, beta_only, label='beta damping', lw=1, color='black', linestyle='dashdot')
    ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=16)

    # レイアウト設定
    fig.tight_layout()

    # グラフを表示する。
    plt.show()
    plt.close()
    # ---------------------------------------------------

# 固有角振動数を周波数を指定して定義
w1 = 2 * np.pi * 10
w2 = 2 * np.pi * 1000

# 減衰比を設定
zeta1 = 0.01
zeta2 = 0.1

# alpha, betaを計算する関数を実行
alpha, beta = generate_rayleigh_damping(w1, w2, zeta1, zeta2)
print(alpha, beta)

# omegaの範囲を決めてグラフ表示する関数を実行
w = np.arange(10, 1000, 1)
check_rayleigh_damping(alpha, beta, w)

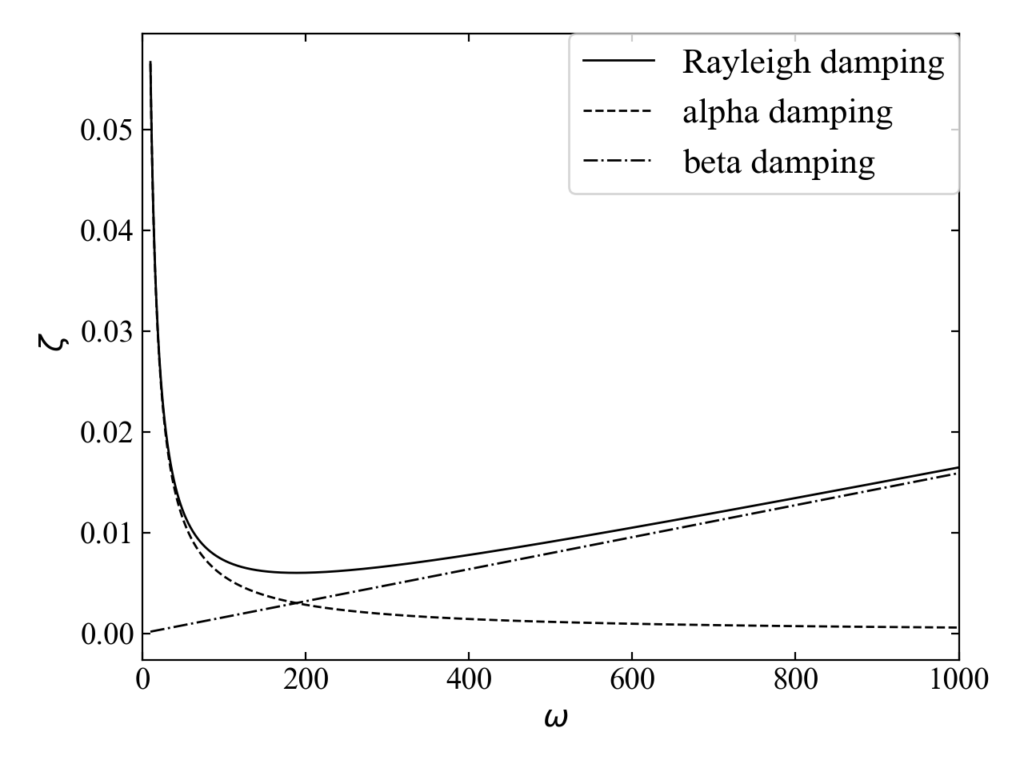
import numpy as np

from matplotlib import pyplot as plt

# Rayleigh dampingのパラメータを決定する関数

def generate_rayleigh_damping(w1, w2, zeta1, zeta2):

alpha = (2 * w1 * w2 * (zeta2 * w1 - zeta1 * w2)) / (w1 ** 2 - w2 ** 2)

beta = (2 * (zeta1 * w1 - zeta2 * w2)) / (w1 ** 2 - w2 ** 2)

return alpha, beta

# Rayleigh dampingを描画する関数

def check_rayleigh_damping(alpha, beta, w):

zeta = (1 / 2) * ((alpha / w) + (beta * w))

alpha_only = (1 / 2) * alpha / w

beta_only = (1 / 2) * beta * w

# ここからグラフ描画-------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('$\ \omega$')

ax1.set_ylabel('$\ \zeta$')

# スケールの設定をする。

ax1.set_xlim(0, 1000)

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

ax1.plot(w, zeta, label='Rayleigh damping', lw=1, color='black')

ax1.plot(w, alpha_only, label='alpha damping', lw=1, color='black', linestyle='dashed')

ax1.plot(w, beta_only, label='beta damping', lw=1, color='black', linestyle='dashdot')

ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=16)

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

# ---------------------------------------------------

# 固有角振動数を周波数を指定して定義

w1 = 2 * np.pi * 10

w2 = 2 * np.pi * 1000

# 減衰比を設定

zeta1 = 0.01

zeta2 = 0.1

# alpha, betaを計算する関数を実行

alpha, beta = generate_rayleigh_damping(w1, w2, zeta1, zeta2)

print(alpha, beta)

# omegaの範囲を決めてグラフ表示する関数を実行

w = np.arange(10, 1000, 1)

check_rayleigh_damping(alpha, beta, w)

以下が結果です。文献等でよく見る曲線を描く事ができました。

Rayleigh damping curve with alpha and beta curve

Pythonの振動解析でレイリー減衰の効果を試してみる

シミュレーションモデル

当ブログではいつも直列のばねマスモデルを使っていましたが、今回シミュレーションモデルはサンプルとして以下の7自由度振動系を使います。

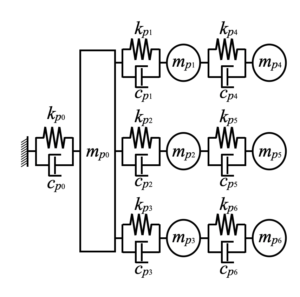
モデルは関数として定義します。剛性行列は「Python/SymPyで連立運動方程式の剛性行列を自動生成する」で自動生成した行列を使いました。この関数の中でgenerate_rayleigh_damping()関数を実行してレイリー減衰を考慮しています。

# シミュレーションモデル
def model():
    # 質量・剛性の集中定数を設定する
    m0 = 0.1
    m1 = 0.2
    m2 = 0.2
    m3 = 0.4
    m4 = 0.5
    m5 = 0.5
    m6 = 0.7
    k0 = 100
    k1 = 1000
    k2 = 4000
    k3 = 5000
    k4 = 6000
    k5 = 9000
    k6 = 10000

    M = np.array([[m0, 0, 0, 0, 0, 0, 0],
                  [0, m1, 0, 0, 0, 0, 0],
                  [0, 0, m2, 0, 0, 0, 0],
                  [0, 0, 0, m3, 0, 0, 0],
                  [0, 0, 0, 0, m4, 0, 0],
                  [0, 0, 0, 0, 0, m5, 0],
                  [0, 0, 0, 0, 0, 0, m6]])

    K = np.array([[k0 + k1 + k2 + k3, -k1, -k2, -k3, 0, 0, 0],
                  [-k1, k1 + k4, 0, 0, -k4, 0, 0],
                  [-k2, 0, k2 + k5, 0, 0, -k5, 0],
                  [-k3, 0, 0, k3 + k6, 0, 0, -k6],
                  [0, -k4, 0, 0, k4, 0, 0],
                  [0, -k5, 0, 0, 0, k5, 0],
                  [0, -k6, 0, 0, 0, 0, k6]])

    # 固有角振動数を周波数を指定して定義
    w1 = 2 * np.pi * 0.1
    w2 = 2 * np.pi * 400

    # 減衰比を設定
    zeta1 = 0.2
    zeta2 = 0.4

    # alpha, betaを計算する関数を実行
    C, alpha, beta = generate_rayleigh_damping(w1, w2, zeta1, zeta2, M, K)

    return M, C, K

# シミュレーションモデル

def model():

# 質量・剛性の集中定数を設定する

m0 = 0.1

m1 = 0.2

m2 = 0.2

m3 = 0.4

m4 = 0.5

m5 = 0.5

m6 = 0.7

k0 = 100

k1 = 1000

k2 = 4000

k3 = 5000

k4 = 6000

k5 = 9000

k6 = 10000

M = np.array([[m0, 0, 0, 0, 0, 0, 0],

[0, m1, 0, 0, 0, 0, 0],

[0, 0, m2, 0, 0, 0, 0],

[0, 0, 0, m3, 0, 0, 0],

[0, 0, 0, 0, m4, 0, 0],

[0, 0, 0, 0, 0, m5, 0],

[0, 0, 0, 0, 0, 0, m6]])

K = np.array([[k0 + k1 + k2 + k3, -k1, -k2, -k3, 0, 0, 0],

[-k1, k1 + k4, 0, 0, -k4, 0, 0],

[-k2, 0, k2 + k5, 0, 0, -k5, 0],

[-k3, 0, 0, k3 + k6, 0, 0, -k6],

[0, -k4, 0, 0, k4, 0, 0],

[0, -k5, 0, 0, 0, k5, 0],

[0, -k6, 0, 0, 0, 0, k6]])

# 固有角振動数を周波数を指定して定義

w1 = 2 * np.pi * 0.1

w2 = 2 * np.pi * 400

# 減衰比を設定

zeta1 = 0.2

zeta2 = 0.4

# alpha, betaを計算する関数を実行

C, alpha, beta = generate_rayleigh_damping(w1, w2, zeta1, zeta2, M, K)

return M, C, K

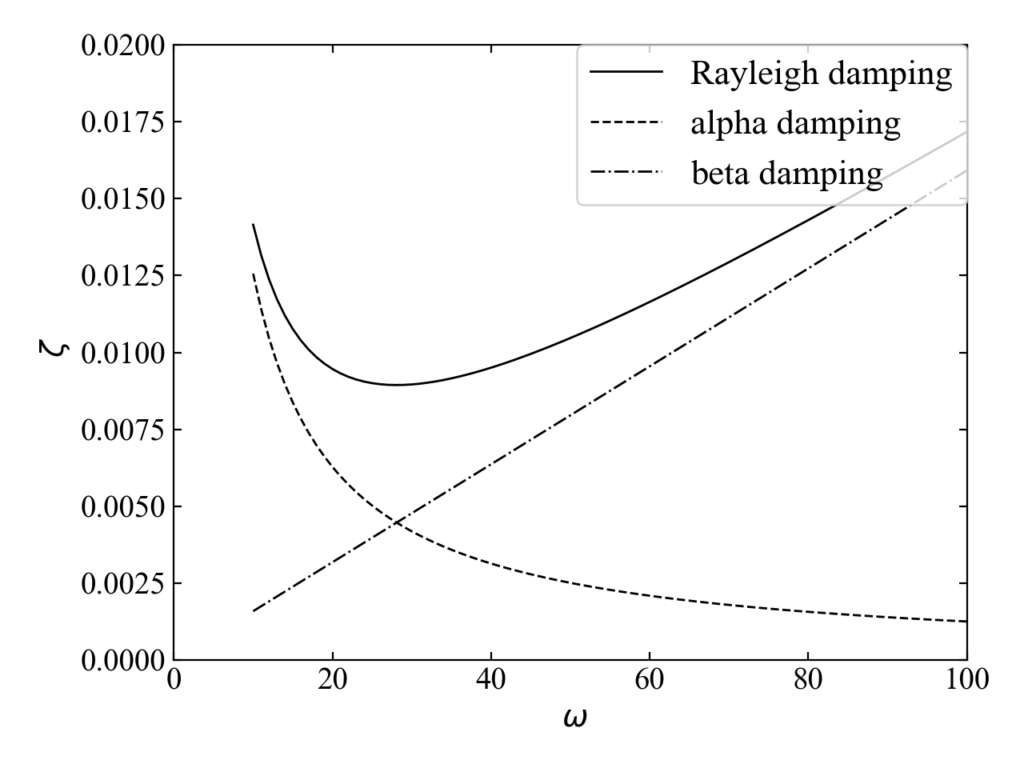
このモデルでは以下のレイリー減衰を設定しています。

シミュレーションコード

周波数応答解析

シミュレーションには周波数応答解析を使います。この方法は「振動モデルを直接法の周波数応答解析で解くPythonコード」を見て頂くと詳細がわかると思います。

以下にシミュレーションを行うコード全文を示します。コピペで動作すると思います。

固有値解析については「Pythonで多自由度系の固有値解析！固有振動数とモードを計算」を参照して下さい。

実行結果

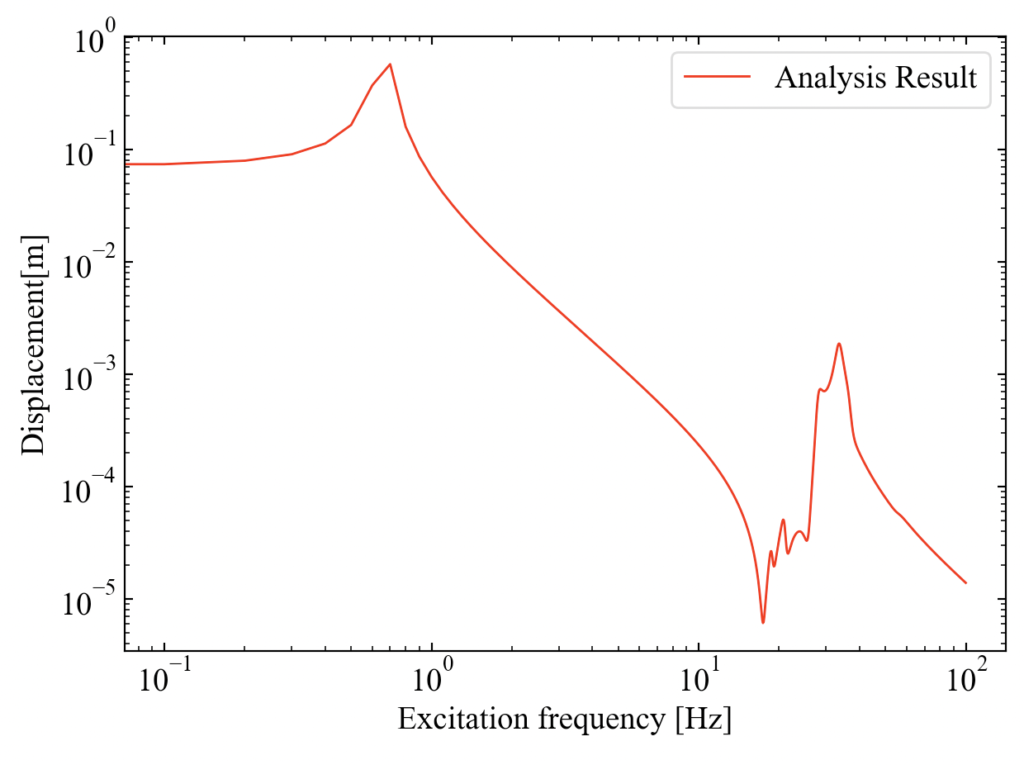
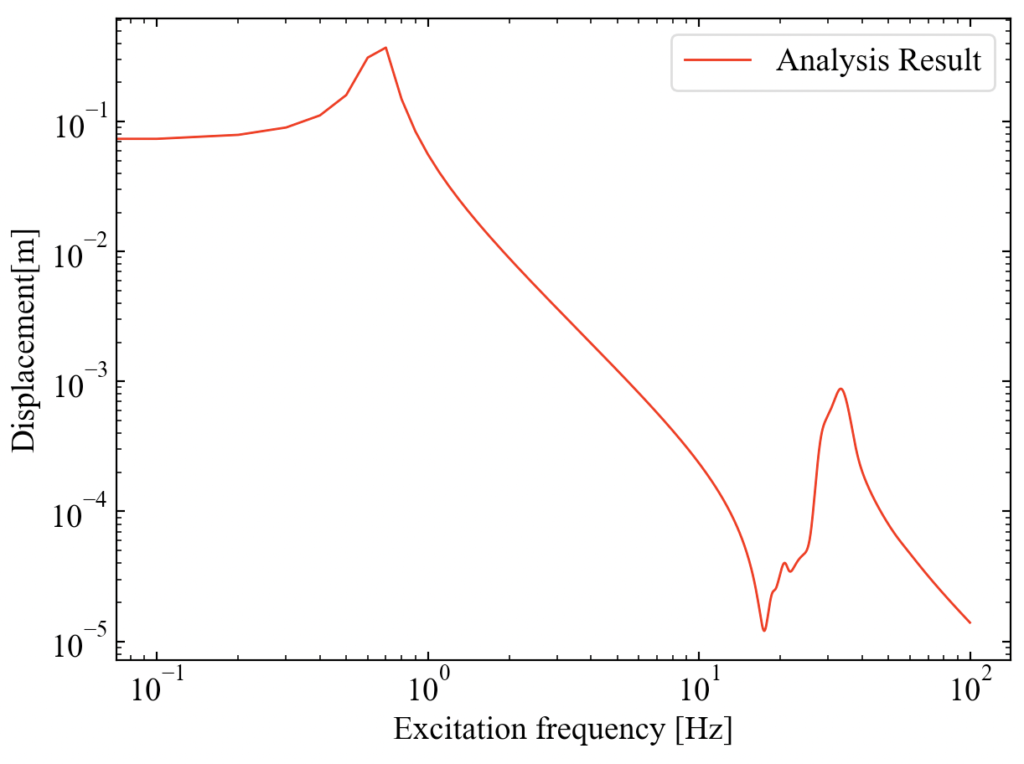
以下がコードの実行結果です。今回の事例だとピークが似通った位置に多くありますが複数ピークが確認できました。

おまけ：減衰比を変えてみる

以下のように減衰比を変更してみます。

# 減衰比を設定
    zeta1 = 0.5
    zeta2 = 0.8

# 減衰比を設定

zeta1 = 0.5

zeta2 = 0.8

ピークの丸みが増し、変更が反映されていることがわかります。周波数毎に減衰比が変わっているはずですが…どうやれば正確な検証ができるんだろう？

まとめ

レイリー減衰について、ちまたでよく聞くので筆者は存在は知っていましたが実際に中身を見てみたのは初めてでした。

式をみてみればレイリー減衰が質量と剛性に対する比例減衰である事、なんちゃって周波数軸で減衰を与えたい事、実は調整が難しそうだという事がよくわかりました。

本記事ではレイリー減衰の式の紹介、これまで覚えたシミュレーションと組み合わせて効果の確認をしてみました。

なんとなく、今後仕事で汎用ソフト等で設定をする時に前よりは適切に設定できそうだと思うようになりました。ただ、もともと減衰というのは奥（闇？）が深いので、できれば減衰パラメータに悩まされない人生をおくりたいものです。

レイリー減衰という特殊な減衰を調べてみました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

Pythonでレイリー減衰を実装する方法！解析して効果を見てみる

レイリー減衰の概要

色々な減衰とレイリー減衰の特徴

レイリー減衰の構成式

Pythonでレイリー減衰曲線を描くコード

Pythonの振動解析でレイリー減衰の効果を試してみる

シミュレーションモデル

シミュレーションコード

周波数応答解析

実行結果

おまけ：減衰比を変えてみる

まとめ

コメント

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

レイリー減衰の概要

色々な減衰とレイリー減衰の特徴

レイリー減衰の構成式

Pythonでレイリー減衰曲線を描くコード

Pythonの振動解析でレイリー減衰の効果を試してみる

シミュレーションモデル

シミュレーションコード

周波数応答解析

実行結果

おまけ：減衰比を変えてみる

まとめ

SNSでもご購読できます。

コメント

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル