
多数の質点系から成る多自由度系は各点の振動が影響し合う連成振動をします。連成振動を解く方法は色々ありますが、ここでは有名な4次のルンゲ・クッタ法をPythonで作成して解いてみます。
こんにちは。wat(@watlablog)です。ここではPythonで作成したルンゲ・クッタコードで多自由度振動問題を解く方法を紹介します!
多自由度振動系の概要
1自由度のおさらい
多自由度振動系の話に行く前に、振動問題を理解するためには1自由度振動系の理解が必要になります。1自由度振動系のモデルは以下の図で表現されます。
当WATLABブログでは「Pythonで1自由度非減衰系の自由振動シミュレーション」より振動シミュレーション系の記事を書き始めました。まずはこちらの記事で1自由度の振動について理解しておくと、この後の話にスムーズに繋がるでしょう。
他にも関連記事として、
「Pythonで1自由度減衰系の自由振動シミュレーション」
「Pythonで1自由度減衰系の強制振動シミュレーション」
に1自由度系の記事を書いていますので、是非減衰系や強制振動の項目も参考にして頂ければと思います。
1自由度振動系のニュートンの運動方程式は式(1)となります。この式は強制振動形式で書いていますが、\(F\)が0になれば自由振動となります。
$$m\ddot{x}+c\dot{x}+kx= F (1)$$
多自由度振動系の運動方程式の立て方
多自由度振動系とは、自由度が複数の振動系です。以下の図は3自由度の非減衰系ですがこれも多自由度振動系と呼びます。
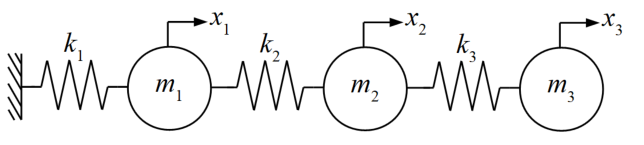
自由度が複数個に増えたと言っても、1自由度系と考え方は変わらず、このモデルの運動方程式は式(2)となります。
$$\mathbf{M}\mathbf{\ddot{x}}+\mathbf{K}\mathbf{x}=\mathbf{F} (2)$$
減衰項も加えれば式(3)となります。
$$\mathbf{M}\mathbf{\ddot{x}}+\mathbf{C}\mathbf{\dot{x}}+\mathbf{K}\mathbf{x}=\mathbf{F} (3)$$
各パラメータが太字になっていますが、これは行列形式で連立方程式を表現したに過ぎません(振動問題を検討する時、通常は自由度の数だけ運動方程式を必要とします)。
このように行列形式で運動方程式を立てた場合、各マトリクスの作り方は「Pythonで計算するために多自由度振動系を行列形式にする方法」に記載しましたので、もし不明な点があればこちらの記事を参考にしてみて下さい。
ルンゲ・クッタ法の概要
数値解析の必要性とルンゲ・クッタを選択する意味
1自由度の振動問題であれば微分方程式の一般解が存在しており、先に紹介した記事ではコードの検証として理論値との比較を行っていました。
しかし自由度が増え、多自由度になると解析的な値を求めることは困難を極め、通常は数値解析を行います。
先ほどの記事ではPythonのscipyというライブラリにあるodeintというメソッドで数値解析を行っていました。
このページでもodeintを使ってサクッと簡単に解析をしようと思いましたが、odeintの中身や引数の受け渡し等を多自由度に対応させる方法がちょっと調べただけではわかりませんでした(お恥ずかしい)。
僕にとってブラックボックスであるodeintを紐解くよりも、既に世間で頻繁に使われているルンゲ・クッタ法を多自由度振動問題に対しnumpyで書いた方が早いと思いました。
→やっとodeintを理解しました。こっちの方が高速に動作するのでお勧めです。
「Pythonで多自由度振動系の過渡応答計算をする時はSciPyを使おう」
…ということで、このページでは主にnumpyを使用して数値解析手法であるルンゲ・クッタ法コードを作成し、多自由度振動問題を数値的に解いていきます。
4次のルンゲ・クッタ法はプログラム的に大変書きやすく、精度や計算速度の関係もバランスの良い手法として知られています。まずはコードが書きやすいというのが、今回ルンゲ・クッタ法を選択した理由です。
ルンゲ・クッタ法(4次)の基本式
数値解析の世界ではオイラー法(Euler Method)がシンプルな手法として有名ですが、精度が悪いことでも有名です。そしてホイン法(Heun Method)といったオイラー法よりも精度が改善された手法もありますが、次に紹介する4次のルンゲ・クッタ法ほどではありません。
ルンゲ・クッタ法(Runge-Kutta Method)は調べれば無数の説明ページが出てくるほど有名な手法で、問題の微分方程式をテイラー展開した時に、4次の項まで一致するという特徴を持ちます。
4次のルンゲ・クッタ法は式(4)で示され、以下に続く係数\(k_{1}, k_{2}, k_{3}, k_{4}\)を使います。
\(y_{i+1}=y_{i}+\frac{1}{6}(k_{1}+2k_{2}+2k_{3}+k_{4}) (4)\)
\(k_{1}=hf(x_{i},y_{i})\)
\(k_{2}=hf(x_{i}+\frac{h}{2},y_{i}+\frac{k_{1}}{2})\)
\(k_{3}=hf(x_{i}+\frac{h}{2},y_{i}+\frac{k_{2}}{2})\)
\(k_{4}=hf(x_{i}+h,y_{i}+k_{3})\)
ここで\(h\)は刻み幅として微小な値を設定します。
詳細な説明や導出はここでは省きますが(導出はかなり大変…)、今回はこの式を使って多自由度振動系の運動方程式を数値解析していきます。
ルンゲ・クッタ法は他にも様々な改良が加えられた派生手法が存在しますが、ここでは一般に古典的ルンゲ・クッタ法と呼ばれる最もコーディングしやすい上式を使います。
4次のRunge-Kuttaで多自由度振動系を解析するコード
今回多自由度振動系の運動方程式をルンゲ・クッタ法で数値解析するにあたり、中々質量・減衰・剛性マトリクスを使った例題を探せませんでしたが、以下①②のWebページを大いに参考にさせて頂きました。
①パソコンで数値計算:ルンゲクッタ法
→複数方程式の扱い方を参考
②Qiita:[Pythonによる科学・技術計算]4次のルンゲ-クッタ法による1次元ニュートン方程式の解法
→Pythonのルンゲ・クッタ法記述スタイルを参考
ありがとうございました。
まずは1自由度振動系で確認
まずはルンゲ・クッタ法の確認として、これまでodeintでやってきたように1自由度振動系のシミュレーションを行い、理論値と比較をしてみます。
以下にコードを示しますが、運動方程式の変換は「Pythonで1自由度減衰系の自由振動シミュレーション」で説明した通りです。運動方程式とパラメータ値はdef関数の中に入れています。
式(4)の\(h\)は\(dt\)と時間刻みという意味合いで与えています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
import numpy as np import matplotlib.pyplot as plt # 運動方程式を関数として定義 def f(x, v): m = 1 # 質量[kg] c = 5 # 減衰係数[N・(s/m)] k = 1000 # 剛性[N/m] y = - (c/m) * v - (k/m) * x # 減衰自由振動モデル return y # 解析条件 t0 = 0.0 # 開始時間 t1 = 1.0 # 終了時間 dt = 0.00001 # 時間刻み # 初期条件 x0 = 0.1 # 初期変位[m] v0 = 1.0 # 初期速度[m/s] x, v = x0, v0 # 初期値に設定 t_axis = np.arange(t0, t1, dt) # 時間軸 x_sol = [] # 初期化x(変位)配列 v_sol = [] # 初期化v(速度)配列 # 4次のRunge-Kutta法による数値解析 for t in t_axis: v_sol.append(v) x_sol.append(x) k11 = f(x, v) * dt k12 = v * dt k21 = f(x + k11 / 2, v + k12 / 2) * dt k22 = (v + k12 / 2) * dt k31 = f(x + k21 / 2, v + k22 / 2) * dt k32 = (v + k22 / 2) * dt k41 = f(x + k31, v + k32) * dt k42 = (v + k32) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 # ここから理論値計算 m = 1 c = 5 k = 1000 cc = 2 * np.sqrt(m * k) zeta = c / cc omega = np.sqrt(k / m) omega_d = omega * np.sqrt(1 - np.power(zeta, 2)) sigma = omega_d * zeta X = np.sqrt(np.power(x0, 2) + np.power((v0 + sigma * x0) / omega_d, 2)) phi = np.arctan((v0 + (sigma * x0)) / (x0 * omega_d)) theory = np.exp(- sigma * t_axis) * X * np.cos(omega_d * t_axis - phi) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Displacement [m]') # データプロット ax1.plot(t_axis, x_sol, label='RK4', c='b', marker='o', linestyle='None') ax1.plot(t_axis, theory, label='Theory', c='r') fig.tight_layout() plt.legend(loc='upper right') # グラフを表示する。 plt.show() plt.close() |
変位と速度という複数方程式がありますが、先ほどの参考Webのようにそれぞれにルンゲ・クッタを適用しています。
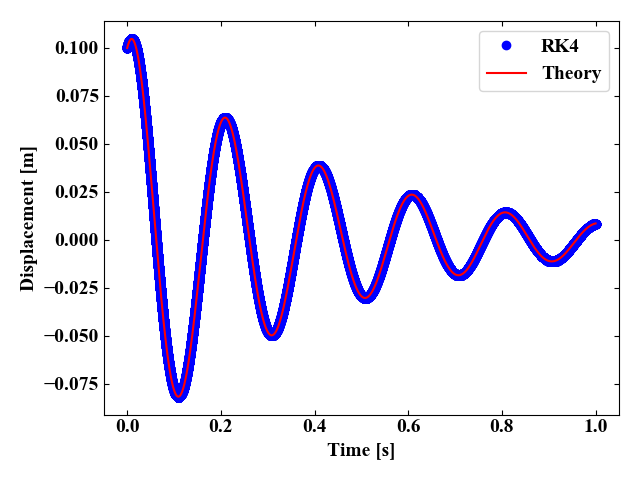
このコードを実行すると以下の結果を得ます。
定量的な誤差は出していませんが、理論値と解析値は良く一致していると言って良い結果を得ました。
多自由度振動系に拡張
2自由度の場合の結果を固有値解析・参考書の例と比較してみる
1自由度で確認がとれたので、続いて多自由度で確認してみます。ここでは2自由度のシミュレーションコードを以下に示します。
def文の中で、行列同士の演算を単に掛け算記号「*」でやってしまうと、numpyの場合要素積になってしまうので、行列演算をするようにnp.dotを使っている所がポイントです。割り算は逆行列を同じくnp.dotでかけるという方法をとっています(順番にも注意)。
2自由度の場合は検証可能な時間波形の例題が見つかりませんでしたので、数値解析で得られた時間波形をフーリエ変換して固有振動数を確認する方法を選びました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
from scipy import fftpack import numpy as np import matplotlib.pyplot as plt # 運動方程式を関数として定義 def f(x, v): # 質量・減衰・剛性の集中定数を設定する m1 = 100 m2 = 50 k1 = 5.0e4 k2 = 1.0e4 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) M_inv = np.linalg.inv(M) # 質量マトリクスの逆行列 # 非減衰自由振動モデル y = - np.dot((np.dot(K, M_inv)), x) return y # 解析条件 t0 = 0.0 # 開始時間 t1 = 5.0 # 終了時間 dt = 1e-4 # 時間刻み # 初期条件 x0 = np.array([[-1.0], [0.0]]) # 初期変位[m] v0 = np.array([[0.0], [0.0]]) # 初期速度[m/s] x, v = x0, v0 # 初期値に設定 t_axis = np.arange(t0, t1, dt) # 時間軸 x_sol = [] # 初期化x(変位)配列 v_sol = [] # 初期化v(速度)配列 # 4次のRunge-Kutta法による数値解析 iteration = 0 for t in t_axis: x_sol.append(x[1, 0]) # 2つ目の自由度の変位を結果として抽出 v_sol.append(v[1, 0]) # 2つ目の自由度の速度を結果として抽出 print('iteration=', iteration,'time=', t) k11 = f(x, v) * dt k12 = v * dt k21 = f(x + k11 / 2, v + k12 / 2) * dt k22 = (v + k12 / 2) * dt k31 = f(x + k21 / 2, v + k22 / 2) * dt k32 = (v + k22 / 2) * dt k41 = f(x + k31, v + k32) * dt k42 = (v + k32) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 iteration += 1 # 検証用の周波数分析 spec = fftpack.fft(x_sol) # 時間波形をフーリエ変換してスペクトルにする abs_spec = np.abs(spec / (len(spec)/2)) # 振幅を計算 frequency = np.linspace(0, 1/dt, len(x_sol)) # 周波数軸を作成 # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Displacement [m]') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Displacement [m]') ax2.set_xlim(0, 10) ax2.set_yscale('log') # データプロット ax1.plot(t_axis, x_sol, label='RK4') ax2.plot(frequency, abs_spec) fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
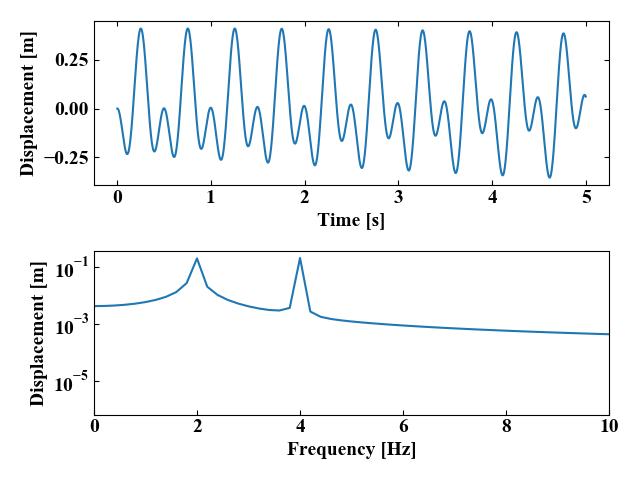
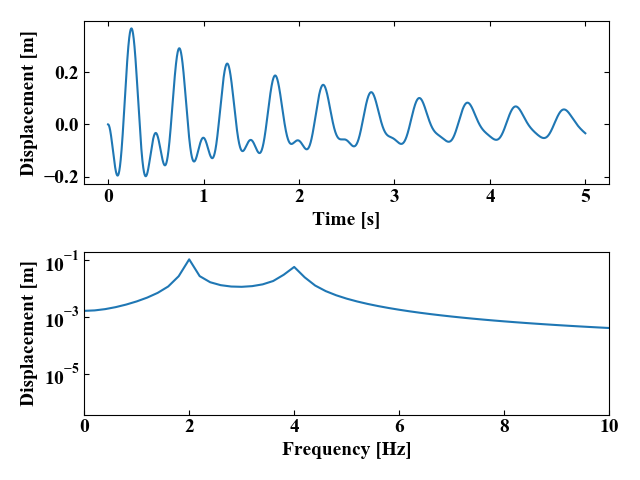
上記コードを実行すると以下の結果を得ます。
時間波形には2つの質点の振動が相互に影響している様子が現れ、周波数波形にはピークが2つ発生していました。
今回は自由振動のモデルで計算を行っているので、これらのピークは固有振動数が近似されているはずです。
このモデルの固有振動数が本当にこの2つのピークなのか、検証のために以下のコードで固有値解析を行ってみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import numpy as np from matplotlib import pyplot as plt # パラメータを設定 m1 = 100 m2 = 50 k1 = 5.0e4 k2 = 1.0e4 # 質量マトリクスと剛性マトリクスを作成 M = np.array([[m1, 0], [0, m2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソート omega_sort = np.sort(omega) # 固有値のソート時のインデックスを取得 # ⇒固有ベクトルと対応させるため sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) # 結果をコンソールに表示 print(np.sqrt(omega_sort) /(2 * np.pi)) |
ちなみに、固有値解析のコードは「Pythonで多自由度系の固有値解析!固有振動数とモードを計算」で書いたものを使用しています(最後の固有角振動数を固有振動数として周波数に変換している所が異なる程度)。
この記事には固有ベクトル(モードシェイプ)の確認方法等も記載していますので、是非今回の数値解析と併用してみて下さい。
上記固有値解析のコードを実行すると、以下の結果を得ます。
固有振動数は2つ持ち、それぞれ約2[Hz], 4[Hz]と、先ほどのグラフと対応していることがわかりました。
|
1 |
[1.98178918 4.04187436] # 固有振動数[Hz] |
そして最後はダメ押しです。今回使用した質量と剛性のパラメータは「モード解析入門」という参考書のP130、3.4数値例に記載されたものです。
参考書の結果も1.98[Hz], 4.04[Hz]となっているので、周波数は数値解析、固有値解析、参考書で矛盾はありませんでした。
初めての多自由度系の数値解析プログラムだったので正直不安でしたが、どうやら固有振動数レベルでは問題無いように見えます。
減衰マトリクスを追加してみる
続いてさらに汎用性を高めるために、減衰係数[N・(s/m)]を行列形式にした減衰マトリクスを追加してみます。多自由度振動系ルンゲ・クッタコード内def関数の中の定数とマトリクス、モデルの式\(y\)を変更しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 運動方程式を関数として定義 def f(x, v): # 質量・減衰・剛性の集中定数を設定する m1 = 100 m2 = 50 c1 = 50 c2 = 50 k1 = 5.0e4 k2 = 1.0e4 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) M_inv = np.linalg.inv(M) # 質量マトリクスの逆行列 # 減衰自由振動モデル y = - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y |
時間波形は徐々に振動が小さくなっていく様子が、そして周波数波形はピークが鈍って減衰の影響が反映されたことがわかりました。
強制振動モデルとして外力をかけてみる
最後に以下のコードで外力ベクトルを設定、モデルにも外力項を追加して強制振動モデルにしてみました。先ほどと同じくモデルの変更はdef文の中を変更するだけです。
今回は単なる外力が反映されるかどうかの確認なので、トンデモ力を4[Hz]と共振にぶちあてるような感じで与えています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 運動方程式を関数として定義 def f(x, v): # 質量・減衰・剛性の集中定数を設定する m1 = 100 m2 = 50 c1 = 50 c2 = 50 k1 = 5.0e4 k2 = 1.0e4 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) M_inv = np.linalg.inv(M) # 質量マトリクスの逆行列 # 外力ベクトル F = np.array([[0.0], [1.0e20 * np.cos(2 * np.pi * 4.0 * t)]]) # 減衰強制振動モデル y = np.dot(M_inv, F) - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y |
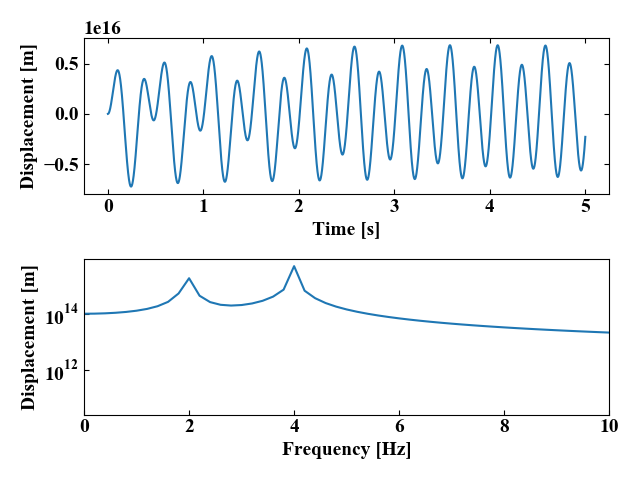
…やりすぎました。これは地球がやばい。
以下がコード実行結果ですが、プロットの縦軸がトンデモ無い値になっています。そして4[Hz]のピークが第一ピークよりも高くなっています。計算の目的からすると、外力が働いていることが確かめられたので良しとします。
自由度を増やす場合は上記コードの質量・減衰・剛性に関する正方マトリクスや、初期変位ベクトル、初期速度ベクトル、外力ベクトルをそれぞれ増やしていくだけです。
インパルス加振
インパルス加振(ハンマーで叩いたような加振力)も実装してみます。また、コードも少し整理してみましょう。
1自由度でも多自由度でも同じコードが使えるように、さらに簡単なDocstringも記載、プロットも関数として定義してメイン処理はif...の書き方にしました。
インパルス加振なので、周波数特性は周波数応答関数を計算するコードも追記しています。周波数応答関数については「Pythonで伝達関数!2つの信号の周波数応答関数を計算する方法」をご覧ください。
1自由度
まずは1自由度の場合のシミュレーションコードを示します。条件は先ほどと同じ。初期条件は全て0にして加振させています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt def model_1dof(): ''' 質量、減衰、剛性マトリクスを定義 ''' # 質量m・減衰c・剛性kの集中定数を設定する m1 = 1.0 c1 = 5.0 k1 = 1000.0 # マトリクス化 M = np.array([[m1]]) C = np.array([[c1]]) K = np.array([[k1]]) return M, C, K def f(x, v, f, M, C, K): ''' 運動方程式 ''' # 質量マトリクスの逆行列 M_inv = np.linalg.inv(M) # 外力ベクトルの初期化 F = np.zeros(len(M)) F[0] = f # 減衰強制振動モデル y = np.dot(M_inv, F) - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y def sim(M, C, K): ''' シミュレーションを4次のRunge-Kutta法で実行する ''' # 解析条件 t0 = 0.0 t1 = 3.0 dt = 1e-4 # 初期化:x0[m], v0[m/s] x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) x, v = x0, v0 t_axis = np.arange(t0, t1, dt) x_sol = [] v_sol = [] # インパルス波形を加振力に設定 force = np.zeros(len(t_axis)) force[1:2:1] = 1 # 4次のRunge-Kutta法による数値解析(外力成分を離散1D波形から抽出するバージョン) iteration = 0 for t in t_axis: # 1自由度目の変位と速度をappend x_sol.append(x[0]) v_sol.append(v[0]) # イタレーションをモニタ if iteration % 100 == 0: print('iteration=', iteration, 'time=', t, force[iteration]) # Runge-Kuttaのメイン k11 = f(x, v, force[iteration], M, C, K) * dt k12 = v * dt k21 = f(x + k11 / 2, v + k12 / 2, force[iteration], M, C, K) * dt k22 = (v + k12 / 2) * dt k31 = f(x + k21 / 2, v + k22 / 2, force[iteration], M, C, K) * dt k32 = (v + k22 / 2) * dt k41 = f(x + k31, v + k32, force[iteration], M, C, K) * dt k42 = (v + k32) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 iteration += 1 return force, x_sol, dt, t_axis def eigen(M, K): ''' 固有値解析 ''' # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return h_io, amp, phase, freq def plot(t_axis, input, output, freq, phase, amp): ''' plot ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 6)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(222) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(224) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') # スケールの設定をする。 ax3.set_xlim(0.1, 100) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax3.set_xscale('log') ax4.set_xlim(0.1, 100) ax4.set_ylim(1e-8, 1e-3) ax4.loglog() # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='1dof', lw=1, color='red') ax2.plot(t_axis, output, label='1dof', lw=1, color='red') ax3.plot(freq, phase, label='1dof', lw=1, color='red') ax4.plot(freq, amp, label='1dof', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' # 1自由度振動系の過渡応答解析 M, C, K = model_1dof() eigen_value1, eigen_vector1 = eigen(M, K) input, output, dt, t_axis = sim(M, C, K) print(eigen_value1) # FRFを関数を実行して計算 h_io, amp, phase, freq = frf(input, output, 1 / dt) # プロット plot(t_axis, input, output, freq, phase, amp) |
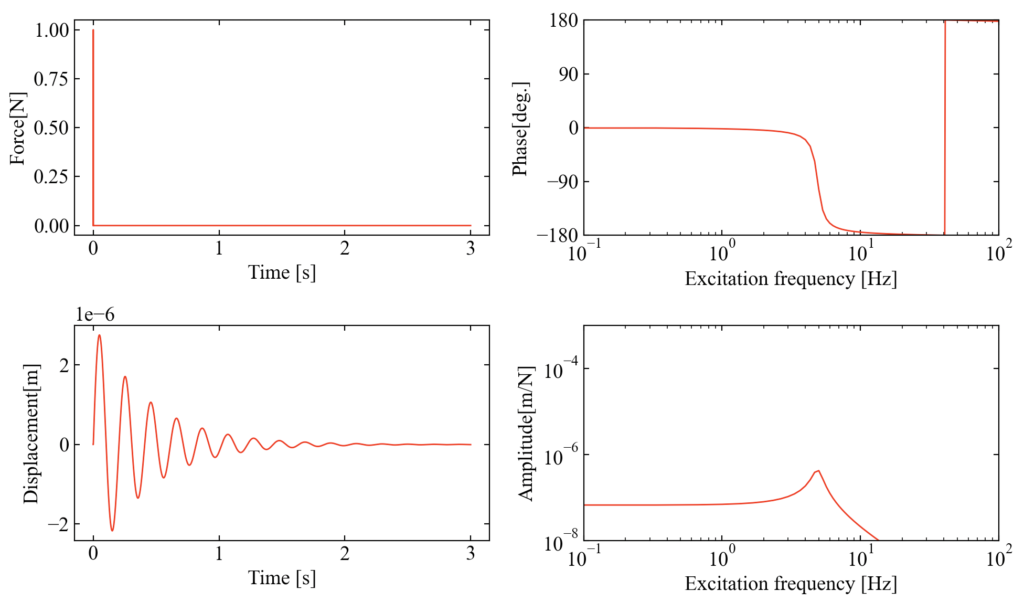
2自由度
次は2自由度モデルの場合です。def model_2dofという関数で振動系を定義することで、主要なコードは変更せずにモデルだけ変えることができました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt def model_1dof(): ''' 質量、減衰、剛性マトリクスを定義(1自由度モデル) ''' # 質量m・減衰c・剛性kの集中定数を設定する m1 = 1.0 c1 = 5.0 k1 = 1000.0 # マトリクス化 M = np.array([[m1]]) C = np.array([[c1]]) K = np.array([[k1]]) return M, C, K def model_2dof(): ''' 質量、減衰、剛性マトリクスを定義(2自由度モデル) ''' # 質量m・減衰c・剛性kの集中定数を設定する m1 = 100 m2 = 50 c1 = 50 c2 = 50 k1 = 5.0e4 k2 = 1.0e4 M = np.array([[m1, 0], [0, m2]]) C = np.array([[c1 + c2, -c2], [-c2, c2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) return M, C, K def f(x, v, f, M, C, K): ''' 運動方程式 ''' # 質量マトリクスの逆行列 M_inv = np.linalg.inv(M) # 外力ベクトルの初期化 F = np.zeros(len(M)) F[0] = f # 減衰強制振動モデル y = np.dot(M_inv, F) - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y def sim(M, C, K): ''' シミュレーションを4次のRunge-Kutta法で実行する ''' # 解析条件 t0 = 0.0 t1 = 10.0 dt = 1e-4 # 初期化:x0[m], v0[m/s] x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) x, v = x0, v0 t_axis = np.arange(t0, t1, dt) x_sol = [] v_sol = [] # インパルス波形を加振力に設定 force = np.zeros(len(t_axis)) force[1:2:1] = 1 # 4次のRunge-Kutta法による数値解析(外力成分を離散1D波形から抽出するバージョン) iteration = 0 for t in t_axis: # 1自由度目の変位と速度をappend x_sol.append(x[0]) v_sol.append(v[0]) # イタレーションをモニタ if iteration % 100 == 0: print('iteration=', iteration, 'time=', t, force[iteration]) # Runge-Kuttaのメイン k11 = f(x, v, force[iteration], M, C, K) * dt k12 = v * dt k21 = f(x + k11 / 2, v + k12 / 2, force[iteration], M, C, K) * dt k22 = (v + k12 / 2) * dt k31 = f(x + k21 / 2, v + k22 / 2, force[iteration], M, C, K) * dt k32 = (v + k22 / 2) * dt k41 = f(x + k31, v + k32, force[iteration], M, C, K) * dt k42 = (v + k32) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 iteration += 1 return force, x_sol, dt, t_axis def eigen(M, K): ''' 固有値解析 ''' # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return h_io, amp, phase, freq def plot(t_axis, input, output, freq, phase, amp): ''' plot ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 6)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(222) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(224) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') # スケールの設定をする。 ax3.set_xlim(0.1, 100) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax3.set_xscale('log') ax4.set_xlim(0.1, 100) #ax4.set_ylim(1e-8, 1e-3) ax4.loglog() # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='1dof', lw=1, color='red') ax2.plot(t_axis, output, label='1dof', lw=1, color='red') ax3.plot(freq, phase, label='1dof', lw=1, color='red') ax4.plot(freq, amp, label='1dof', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' # 1自由度振動系の過渡応答解析 M, C, K = model_2dof() eigen_value1, eigen_vector1 = eigen(M, K) input, output, dt, t_axis = sim(M, C, K) print(eigen_value1) # FRFを関数を実行して計算 h_io, amp, phase, freq = frf(input, output, 1 / dt) # プロット plot(t_axis, input, output, freq, phase, amp) |
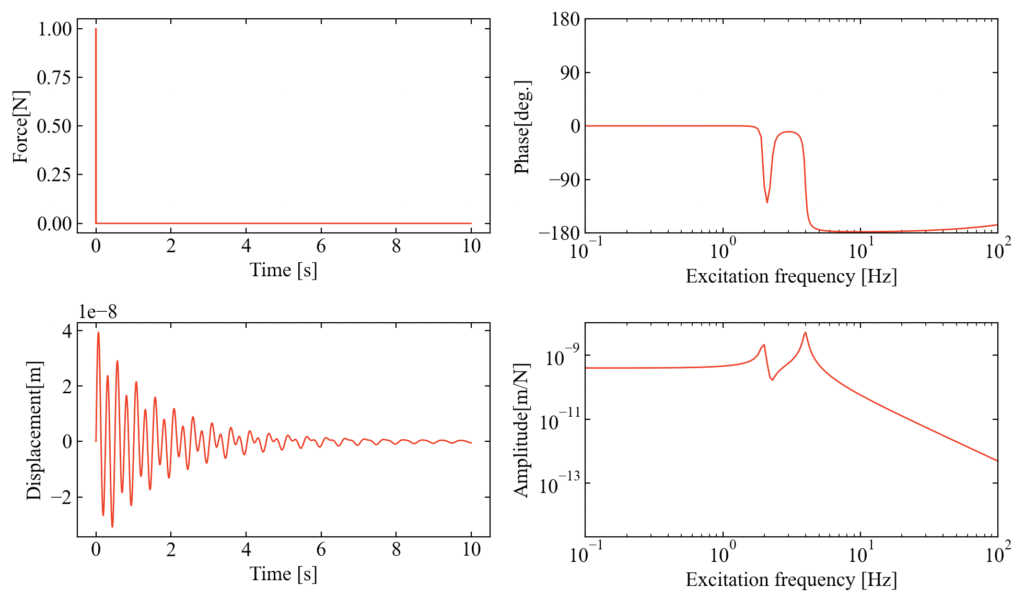
結果はこちら。
サインスイープ加振
インパルス加振と同じくらい使われる加振に、サインスイープ加振があります。
ここではサインスイープ信号をチャープ信号として作ってみましょう。コードは外力部分を置き換えるだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 |
import numpy as np from scipy import fftpack from scipy.signal import chirp import matplotlib.pyplot as plt def model_1dof(): ''' 質量、減衰、剛性マトリクスを定義(1自由度モデル) ''' # 質量m・減衰c・剛性kの集中定数を設定する m1 = 1.0 c1 = 5.0 k1 = 1000.0 # マトリクス化 M = np.array([[m1]]) C = np.array([[c1]]) K = np.array([[k1]]) return M, C, K def model_2dof(): ''' 質量、減衰、剛性マトリクスを定義(2自由度モデル) ''' # 質量m・減衰c・剛性kの集中定数を設定する m1 = 100 m2 = 50 c1 = 50 c2 = 50 k1 = 5.0e4 k2 = 1.0e4 M = np.array([[m1, 0], [0, m2]]) C = np.array([[c1 + c2, -c2], [-c2, c2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) return M, C, K def f(x, v, f, M, C, K): ''' 運動方程式 ''' # 質量マトリクスの逆行列 M_inv = np.linalg.inv(M) # 外力ベクトルの初期化 F = np.zeros(len(M)) F[0] = f # 減衰強制振動モデル y = np.dot(M_inv, F) - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y def sim(M, C, K): ''' シミュレーションを4次のRunge-Kutta法で実行する ''' # 解析条件 t0 = 0.0 t1 = 10.0 dt = 1e-4 # 初期化:x0[m], v0[m/s] x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) x, v = x0, v0 t_axis = np.arange(t0, t1, dt) x_sol = [] v_sol = [] # サインスイープ波形を加振力に設定 force = chirp(t_axis, f0=1, f1=200, t1=t_axis[-1], method='linear') # 4次のRunge-Kutta法による数値解析(外力成分を離散1D波形から抽出するバージョン) iteration = 0 for t in t_axis: # 1自由度目の変位と速度をappend x_sol.append(x[0]) v_sol.append(v[0]) # イタレーションをモニタ if iteration % 100 == 0: print('iteration=', iteration, 'time=', t, force[iteration]) # Runge-Kuttaのメイン k11 = f(x, v, force[iteration], M, C, K) * dt k12 = v * dt k21 = f(x + k11 / 2, v + k12 / 2, force[iteration], M, C, K) * dt k22 = (v + k12 / 2) * dt k31 = f(x + k21 / 2, v + k22 / 2, force[iteration], M, C, K) * dt k32 = (v + k22 / 2) * dt k41 = f(x + k31, v + k32, force[iteration], M, C, K) * dt k42 = (v + k32) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 iteration += 1 return force, x_sol, dt, t_axis def eigen(M, K): ''' 固有値解析 ''' # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return h_io, amp, phase, freq def plot(t_axis, input, output, freq, phase, amp): ''' plot ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 6)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(222) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(224) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') # スケールの設定をする。 ax3.set_xlim(0.1, 100) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax3.set_xscale('log') ax4.set_xlim(0.1, 100) #ax4.set_ylim(1e-8, 1e-3) ax4.loglog() # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='1dof', lw=1, color='red') ax2.plot(t_axis, output, label='1dof', lw=1, color='red') ax3.plot(freq, phase, label='1dof', lw=1, color='red') ax4.plot(freq, amp, label='1dof', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' # 2自由度振動系の過渡応答解析 M, C, K = model_2dof() eigen_value1, eigen_vector1 = eigen(M, K) input, output, dt, t_axis = sim(M, C, K) print(eigen_value1) # FRFを関数を実行して計算 h_io, amp, phase, freq = frf(input, output, 1 / dt) # プロット plot(t_axis, input, output, freq, phase, amp) |
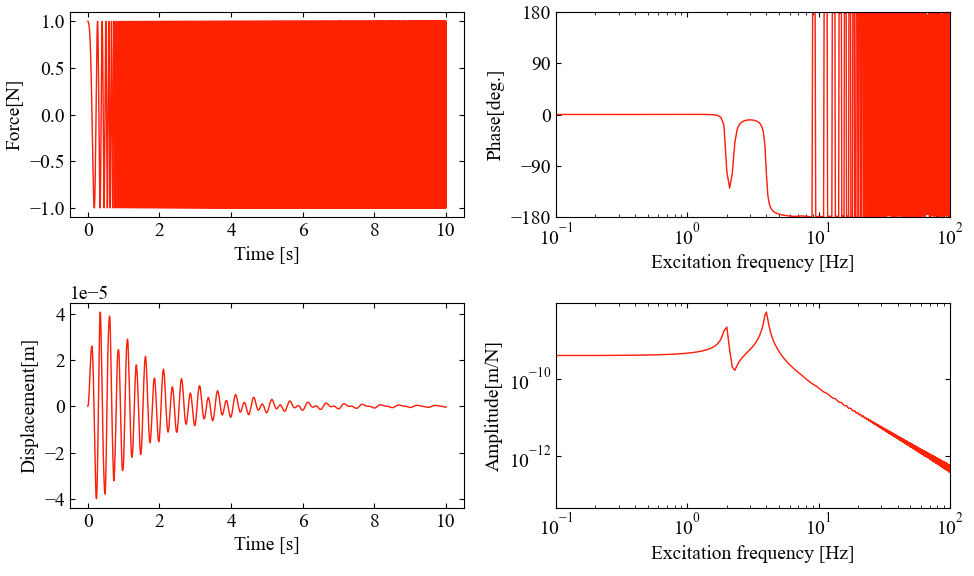
結果はこちら。加振信号は時間進展にともない次第に高周波数になっていく様子がわかります。周波数応答関数は先ほどと同じピークが得られます。
まとめ
本記事は1自由度振動系のおさらいからはじめ、多自由度振動系の問題を4次のルンゲ・クッタ法で数値計算してみました。
1自由度は理論値と、2自由度は固有振動モードと比較しながらPythonコードを作り、非減衰、減衰、強制振動問題で動作を確認しました。
ただやってみた感想ですが、普通のノートPCだと計算が遅いと感じます。
(for文で回しているから?)
もっと効率の良いコードが書ければ良いと思いますが、そもそも速度を重視するのであれば言語の選定も重要ではと感じました。
数値解析はC言語やC++、java、FORTRANが高速計算に向いているとの噂も。
しかし、Pythonによるシミュレーションは機械学習やその他多数の便利ライブラリとの合わせ技を行う場合にメリットがありそうです。
ルンゲ・クッタ法を初めてコーディングしてみました!数値計算は色々な方程式の形を見ることができるので楽しいですね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

先日、コメントさせて頂いたものです。Pythonによる物理シュミレーションの初心者である私に、ここまで丁寧に対応していただきまして、感激しております。
面白かったのは、ばね定数”k1″を大きくすると質点1の振動数も増えておりますが、質点”2”の振動数も大きくなっていることがきちんと描写できている点でした。
当たり前かもしれませんが、質点2に繋がっていないバネ1のバネ定数を変えると、質点2の振動数も変化することが描写出来ていて、改め数値計算の面白さに触れることが出来ました。
(念のため、質点1の変位と速度を抽出するために以下にさせて頂きました)
x_sol.append(x[0, 0]) # 1つ目の自由度の変位を結果として抽出
v_sol.append(v[0, 0]) # 1つ目の自由度の速度を結果として抽出
引き続き、wat様のブログで勉強させていただきたく思います。
今後とも、どうぞよろしくお願いいたします。
ご丁寧に返信誠にありがとうございます!
こちらもまだまだ初心者でして、これを機に学習することができ質問して頂いたことに感謝しています。
僕も初心者であるためおそらく同じ所で面白さを感じていると思います。
今回の解法ができるようになったので、次は制振に使われる2自由度の動吸振器理論もシミュレーションしてみたいと思いました。
今後ともよろしくお願い致します。
最初の減衰振動のコードの
k21 = f(x + dt / 2, v + k11 / 2) * dt
k22 = (v + k11 / 2) * dt
k31 = f(x + dt / 2, v + k21 / 2) * dt
k32 = (v + dt / 2) * dt
k41 = f(x + dt, v + k31) * dt
k42 = (v + k31) * dt
についてですが、ところどころ、式が違ってるような気がします。
k11, k21,k31,k41が、速度に対するオペレーター
k12,k22,k32,k42が、加速度に対するオペレーター
ですよね。その場合、正しくは
k21 = f(x + k11/ 2, v + k12 / 2) * dt
k22 = (v + k11 / 2) * dt
k31 = f(x + k21 / 2, v + k22 / 2) * dt
k32 = (v + k22/ 2) * dt
k41 = f(x + k31, v + k32) * dt
k42 = (v + k32) * dt
ではないですか。例えばk21 = f(x + dt / 2, v + k11 / 2) * dtの右辺、x+dt/2って、fがtの関数になってないのにx+dt/2って変です。f*dtした時のxの次元もおかしくなるし、そもそもxに対する多段影響が入っていない。fortran的に書くと、冗長ですが
K0 = delt*((-c/m)*u0-(k/m)*y0)
L0 = delt*u0
K1 = delt*((-c/m)*(u0+0.5d0*K0)-(k/m)*(y0+0.5d0*L0))
L1 = delt*(u0+0.5d0*K0)
K2 = delt*((-c/m)*(u0+0.5d0*K1)-(k/m)*(y0+0.5d0*L1))
L2 = delt*(u0+0.5d0*K1)
K3 = delt*((-c/m)*(u0+K2)-(k/m)*(y0+L2))
L3 = delt*(u0+0.5d0*K2)
u = u0+(1.0d0/6.0d0)*(K0+2.0d0*K1+2.0d0*K2+K3)
y = y0+(1.0d0/6.0d0)*(L0+2.0d0*L1+2.0d0*L2+L3)
って感じですかね。
ご訪問およびご指摘ありがとうございます!
確かに今見るとdt/2等おかしな表現が目立ちました…。
冒頭の式を拡張する際に勘違いをし、かつ減衰振動理論式とそれなりに合ってしまったのでそのまま進んでしまっていたようです。
まだ何かあるかも知れませんが、検証のきっかけを与えて頂きありがとうございます。
初めまして。
一つお聞きしたいことがあるのですが、2自由度系の本プログラムでは二つ目の質点の変位・速度を出していたのですが、一つ目の質点の変位・速度を知りたい場合は40行目のx_sol.append()の()内を変更すれば求められますか?
その場合どのように変えたらいいでしょうか?
お忙しい中恐縮ですが、ご教授いただければ幸いです。
ご訪問ありがとうございます。
仰る通り、その部分を変更します。
.append(x[1, 0])で2つ目の質点情報を抽出していますが、
.append(x[0, 0])とすることで1つ目の質点情報にすることができます。
ご確認お願い致します。
こんにちは。情報ありがとうございます。
ルンゲ・クッタ法の解説冒頭の式(4)の箇所で、k4=hf(xi+h,yi+h)となっていますが、yiについてはyi+k3となるので、ご訂正をお願いしたいです。
ご指摘頂きありがとうございます!
大変助かります♂️