ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
このブログではしばらく自前のルンゲ・クッタ法を使って振動解析を行ってきました。しかしPythonで常微分方程式の数値計算をする時はSciPyのodeintを使った方が良いです。ここでは巨人の肩に乗るつもりでSciPy/odeintで振動問題を解くための例題を紹介します。
こんにちは。wat(@watlablog)です。ここではようやく使い始めたSciPyのodeintで振動問題の過渡応答解析をするコード例を紹介します！
scipy.integrate.odeintを使った方が良い理由
圧倒的に高速
Pythonで書いた4次のルンゲ・クッタ法の問題点
当WATLABブログでは2020年2月に以下の記事で多自由度振動系を4次のルンゲ・クッタ法で数値計算するコードを紹介しました。この記事はTwitterへのDMやブログのコメントで「多自由度の振動を解析したい」と要望があって書いたものです。
それより前は1自由度の記事でSciPyのodeintを使っていましたが、当時はスキル不足からどうしても多自由度化のコードが書けず、odeintで多自由度の問題を解くのは保留していました。
0からスクラッチで書くルンゲ・クッタ法のコードであればブラックボックスにはならないだろうという理由だけです。
ところが自前のルンゲ・クッタ法コードはとにかく計算が遅いです。Pythonでforループを使っていることもあり、数十秒の計算を時間刻み1e-4[s]程度で解こうものなら結構待ちます。NumbaをインストールしてJITを適用しても気休め程度でした。
さらに自前の手法は方程式がいわゆるスティッフな系（硬い方程式）だとすぐに発散してしまいました。これは数値解析を専門にしている人であれば、さらにアルゴリズムを改良して解決していくと思いますが、筆者にはハードルが高すぎました。
ちなみにNumbaもPython高速化に関するライブラリです。こちらを参考にしてください。
odeintはFORTRANライブラリを使用している
SciPyのodeintは公式ドキュメントによるとFORTRANのodepackというライブラリを使用しているそうです。数値解析の分野では現役でFORTRANが使われていますが、やはり速度はFORTRANかC言語系（最近ではJuliaも？）が強いです。
Solve a system of ordinary differential equations using lsoda from the FORTRAN library odepack.
scipy.integrate.odeint:https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html
車輪の再発明で新しいバグを仕込む心配が少ない
先ほどのルンゲ・クッタ法の記事内コメント欄を確認していただければわかりますが、記事公開後、色々な人にご指摘をいただきコードを修正してきました。この辺はブログをやっていてよかった点ですが、やはり自前で用意したコードはバグが潜むリスクを多く持ちます。
0からアルゴリズムを書くのは勉強としてやってよかったと思いますが、ルンゲ・クッタ法等は既に先人達がパッケージングして誰でも使える状態にしてくれています。そちらの方がより多くのレビューを受けているのでバグの可能性は低くなるでしょう（ないとは言えませんが）。
今回は久しぶりにSciPyのodeintを使ってみたら、多自由度でも特に悩まず使えたのでその方法を紹介します。
scipy.integrate.odeintで振動解析をするPythonコード例
動作環境
この記事は以下のPython環境でコードの動作を確認しました。
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| Scipy | 1.4.1 |
| Pandas | 1.0.5 |
| matplotlib | 3.4.3 |
| pillow | 7.1.2 |
1自由度非減衰自由振動
odeintを使った振動解析コードですが、せっかくなので1自由度非減衰系の自由振動から順を追って紹介します。
1自由度非減衰系の自由振動は下図のモデルで表現されます。
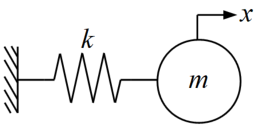
続いて運動方程式を式（1）に示します。
\[
m\ddot{x}+kx=0
\tag{1}
\]
式（1）をodeintで計算するコードを以下に示します。
メイン部分（コードの下部分）で以下の流れとなっています。
- モデルを定義する。
- 解析時間を設定する。
- 初期条件を設定する。
初期条件は1D配列にする必要があるためvarとまとめています。 - odeintを呼び出して計算する。
関数fを呼び出し、varとt、その後ろに変数をまとめてargs=()で設定します。
呼び出された関数f内部で初期条件で指定した1D配列変数を分離させ、運動方程式に組み込みます。
結果をreturnに設定しますが、returnは1D配列になるようにします。
この1D配列にするというのがodeintを使う時のキーポイントになります。 - 結果のフォーマットを揃える。
計算されたvarは列方向が変数、行方向が時間であるため、転置してから指標で抽出することで時間波形を取得できます。 - グラフに描画する。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
import numpy as np from matplotlib import pyplot as plt from scipy.integrate import odeint def f(var, t, m, k): ''' Harmonic oscillator ''' # x, vに分離 x = var[0] v = var[1] # 運動方程式 a = -(k / m) * x # 結果 output = np.array([v, a]) return output def plot(t, x): ''' Plot ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' Main ''' # モデルを定義 m = 1.0 k = 10.0 # 解析時間 dt = 1e-3 t_max = 10.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = 1.0 v0 = 0.0 var = [x0, v0] # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(m, k)) # 結果を分離 x = var.T[0] v = var.T[1] # プロット plot(t, x) |
運動方程式は「Pythonで1自由度非減衰系の自由振動シミュレーション」で説明したように変数変換を使って表現しており、今後もこのスタイルで書いていきます。
このコードを実行すると以下の結果を得ます。非減衰の自由振動なのでずっと振動する結果となります。
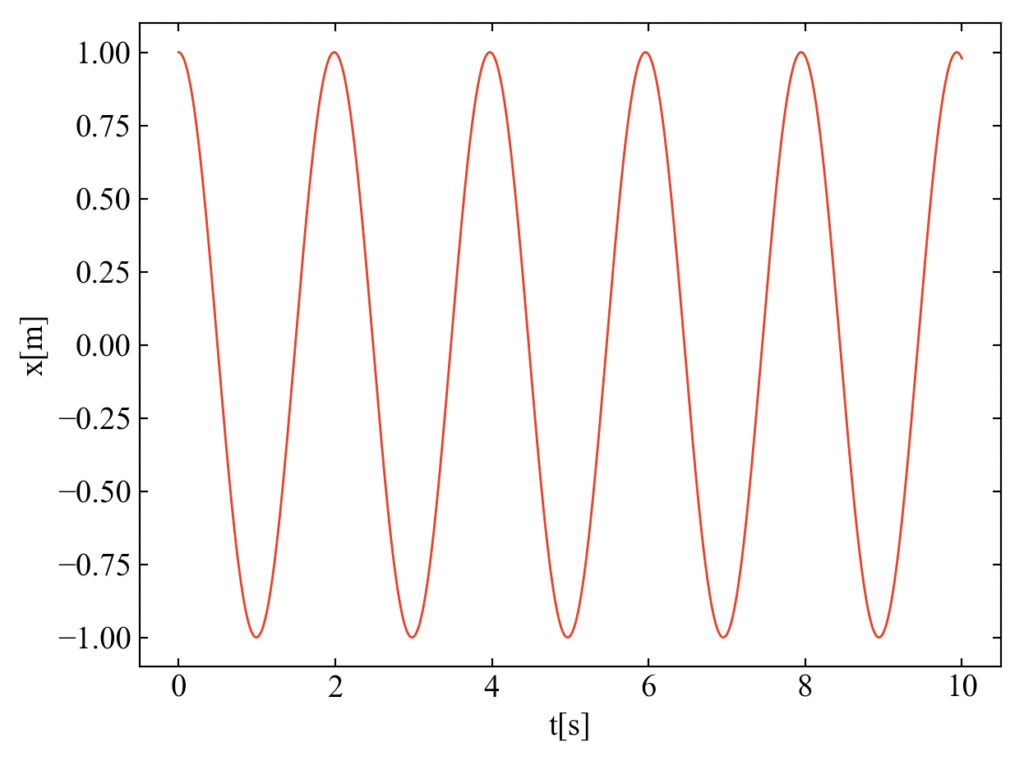
1自由度減衰自由振動
下図のようにダッシュポットを追加し、減衰をモデル化すると運動方程式は式（2）となります。
\[
m\ddot{x}+c\dot{x}+kx=0
\tag{2}
\]
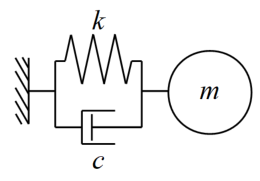
コードを以下に示します。パラメータの設定と運動方程式部分を修正しただけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
import numpy as np from matplotlib import pyplot as plt from scipy.integrate import odeint def f(var, t, m, k, c): ''' Harmonic oscillator ''' # x, vに分離 x = var[0] v = var[1] # 運動方程式 a = - (k / m) * x - (c / m) * v # 結果 output = np.array([v, a]) return output def plot(t, x): ''' Plot ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' Main ''' # モデルを定義 m = 1.0 k = 10.0 c = 1.0 # 解析時間 dt = 1e-3 t_max = 10.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = 1.0 v0 = 0.0 var = [x0, v0] # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(m, k, c)) # 結果を分離 x = var.T[0] v = var.T[1] # プロット plot(t, x) |
減衰振動が確認できました。減衰係数cの値次第で過減衰、臨界減衰、減衰振動の3パターンの振る舞いをしますが、詳細は「Pythonで1自由度減衰系の自由振動シミュレーション」の記事をご確認ください。
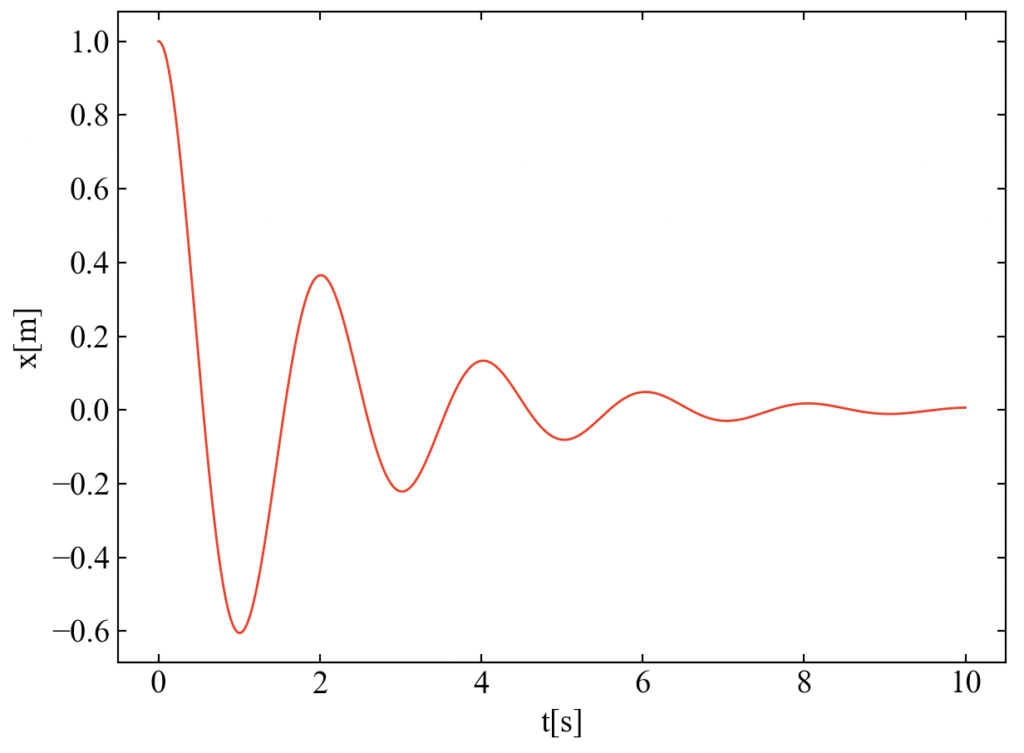
1自由度減衰強制振動（サインスイープ加振）
次は強制振動問題を扱ってみます。SciPyのodeintで強制振動を扱う時は、odeintで呼びだす関数fの中で外力を定義する必要があります。
強制振動の運動方程式は式（3）です。外力が追加されました。
\[
m\ddot{x}+c\dot{x}+kx=f
\tag{3}
\]
ここではサインスイープ信号（チャープ信号）を扱ってみましょう。サインスイープは式（4）で与えます。\(f_{0}\)と\(f_{1}\)の順番を変更することでアップスイープやダウンスイープを切り替えることが可能です。
\[
\alpha = \frac{f_{1} - f_{0}}{t_{max}}\\
f = A \sin \left \{ 2 \pi (f_{0} t + \frac{\alpha}{2}t^{2}) \right \}
\tag{4}
\]
コードを以下に示します。せっかくサインスイープで外力を与えるので、周波数応答関数を計算してみます。周波数応答関数については「Pythonで伝達関数！2つの信号の周波数応答関数を計算する方法」の記事を参照してください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint def f(var, t, m, k, c, A, alpha, f0): ''' Harmonic oscillator ''' # x, vに分離 x = var[0] v = var[1] # 外力を計算 force = A * np.sin(2 * np.pi * (f0 * t + (alpha / 2) * t ** 2)) # 運動方程式 a = - (k / m) * x - (c / m) * v + force # 結果 output = np.array([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' Plot ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 6)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールを設定する。 ax3.set_xlim(0.0, 50.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' Main ''' # モデルを定義 m = 1.0 k = 1000.0 c = 1.0 # 解析時間 dt = 1e-3 t_max = 20.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = 0.0 v0 = 0.0 var = [x0, v0] # 外力（チャープ信号）を計算 f0 = 1 f1 = 50 A = 100.0 alpha = (f1 - f0) / t_max force = A * np.sin(2 * np.pi * (f0 * t + (alpha / 2) * t ** 2)) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(m, k, c, A, alpha, f0)) # 結果を分離 x = var.T[0] v = var.T[1] # FRF(周波数応答関数)を計算 amp, freq = frf(force, x, 1 / dt) # プロット plot(t, x, force, amp, freq) |
結果はこちら。変位の波形で途中から振幅が大きくなっているのはサインスイープの周波数がちょうど共振にあたっているからです。周波数応答関数は約5Hzにピークを保ちますが、この系の固有振動数が \(f_{n}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}=5.03\)[Hz]から説明できます。
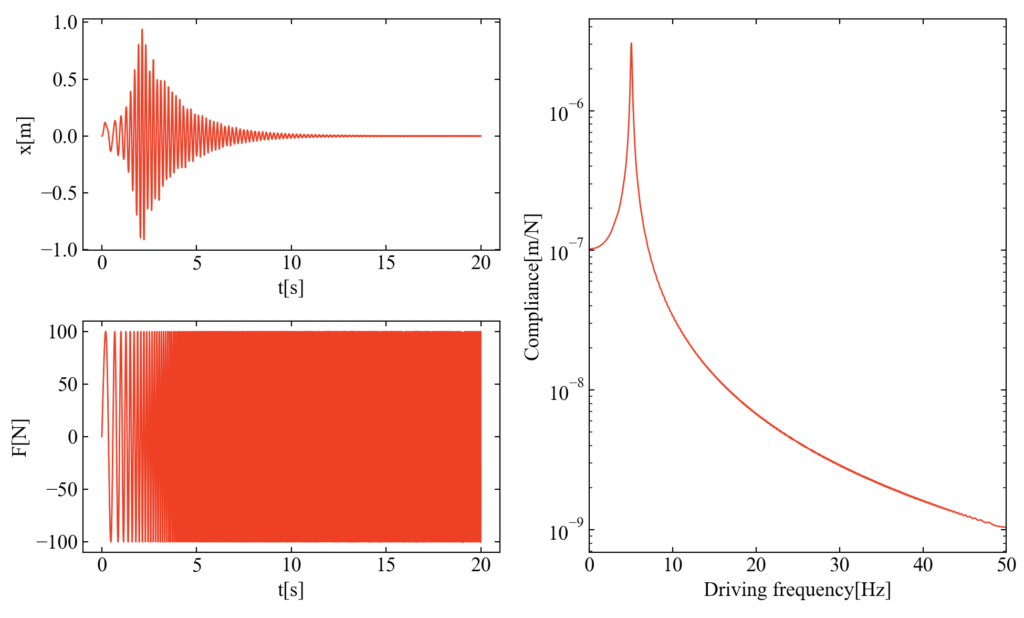
1自由度減衰強制振動（インパルス加振）
外力をインパルス加振に変更した場合のコードを以下に示します。odeintで外力を指定する時は時間の関数にする必要がありますが、プログラミングであれば時間\(t\)をif文の判定に使ってインパルス形状を作成することも可能です（一般的なやり方は他にあるかも？）。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint def f(var, t, m, k, c, A, start, end): ''' Harmonic oscillator ''' # x, vに分離 x = var[0] v = var[1] # 外力を計算 if (t >= start) & (t <= end): force = A else: force = 0.0 # 運動方程式 a = - (k / m) * x - (c / m) * v + force # 結果 output = np.array([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' Plot ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 6)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールを設定する。 ax3.set_xlim(0.0, 50.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' Main ''' # モデルを定義 m = 1.0 k = 1000.0 c = 1.0 # 解析時間 dt = 1e-3 t_max = 20.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = 0.0 v0 = 0.0 var = [x0, v0] # 外力（インパルス加振）を計算 force = np.zeros_like(t) A = 100.0 start = 0.0 end = 0.001 force = np.where((t >= start) & (t <= end), A, 0) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(m, k, c, A, start, end)) # 結果を分離 x = var.T[0] v = var.T[1] # FRF(周波数応答関数)を計算 amp, freq = frf(force, x, 1 / dt) # プロット plot(t, x, force, amp, freq) |
こちらが結果です。外力はインパルス加振になりましたが、モデルのパラメータは変更していないので固有振動数は一緒です。
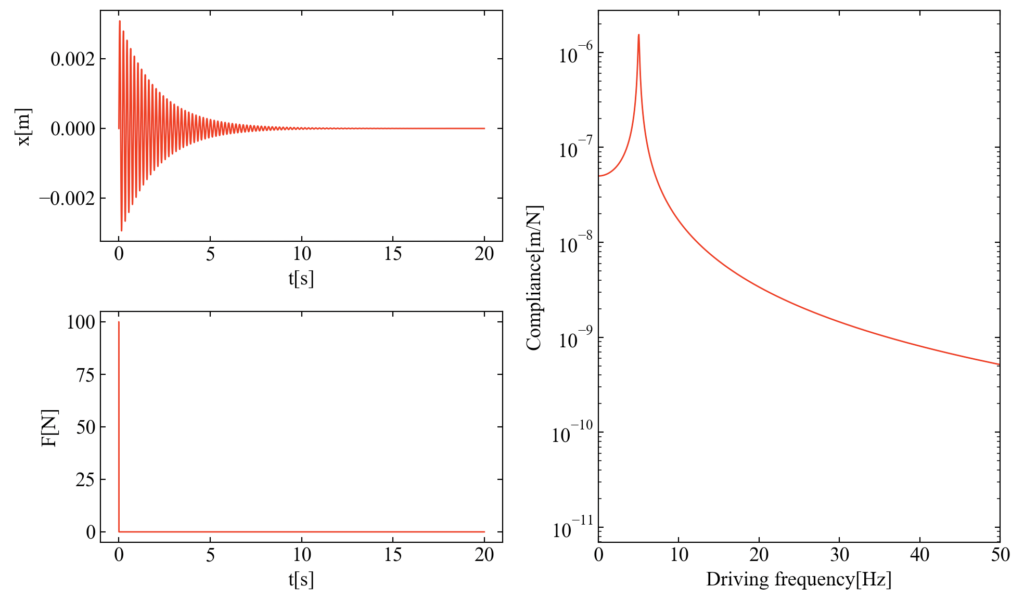
2自由度減衰強制振動（サインスイープ加振）
ここからが本題。odeintで多自由度を表現する方法を紹介します。まずは2自由度から。
今回扱うモデルは以下の2自由度振動系です。
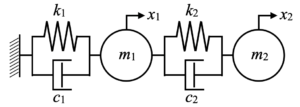
運動方程式の形は式（5）で示す通り1自由度系と同じですが、質量・剛性・減衰は行列形式、変位・速度・加速度・外力はベクトル形式になっています。
\[
\mathbf{M}\mathbf{\ddot{x}} + \mathbf{C}\mathbf{\dot{x}} + \mathbf{K}\mathbf{x}=\mathbf{F}
\tag{5}
\]
行列とベクトルの中身も書いた運動方程式は式（6）となります。この運動方程式の導出方法は「Pythonで計算するために多自由度振動系を行列形式にする方法」や「csvの値から直列ばねマスモデルを自動生成するPythonコード」をご確認ください。
\[
\begin{bmatrix}
m_{1} &0 \\
0 &m_{2}
\end{bmatrix}
\begin{bmatrix}
\ddot{x}_{1}\\
\ddot{x}_{2}
\end{bmatrix}
+
\begin{bmatrix}
c_{1}+c_{2} &-c_{2} \\
-c_{2} &c_{2}
\end{bmatrix}
\begin{bmatrix}
\dot{x}_{1}\\
\dot{x}_{2}
\end{bmatrix}
+
\begin{bmatrix}
k_{1}+k_{2} &-k_{2} \\
-k_{2} &k_{2}
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2}
\end{bmatrix}
=
\begin{bmatrix}
f_{1}\\
f_{2}
\end{bmatrix}
\tag{6}
\]
以下に例題のコードを示します。ここではxやFの値を[-1]で抽出しています（最後の質点を加振し、最後の質点の結果を表示）。
多自由度を扱う時の注意点ですが、初期値や結果を1D配列で扱うことが挙げられます（ブログ開始間もない当時の筆者はこれに気づかなかった…）。初期値varや結果outputをnp.concatnate()で結合した形でodeintに渡しています。
計算結果としてのvarはmatplotlibで表示させるために、前処理としてそれぞれの変数（変位と速度）に分離しています。
変位と速度は同じ数だけあるので、半分で分離すれば必ず分けることが可能です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint def model(): ''' Define model ''' # 質量・減衰・剛性の集中定数を設定する m1 = 100 m2 = 50 k1 = 5.0e4 k2 = 1.0e4 c1 = 5 c2 = 5 M = np.array([[m1, 0], [0, m2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) C = np.array([[c1 * c2, -c2], [-c2, c2]]) return M, K, C def f(var, t, M, K, C, A, k, f0): ''' Harmonic oscillator ''' # 質量行列の逆行列 M_inv = np.linalg.inv(M) # 外力 F = np.zeros(len(M)) F[-1] = A * np.sin(2 * np.pi * (f0 * t + (k / 2) * t ** 2)) # x, vに分離 x = var[0:int(len(var) / 2)] v = var[int(len(var) / 2)::] # 運動方程式 a = - (M_inv @ K) @ x - (M_inv @ C) @ v + (M_inv @ F) # 結果を平坦化（odeint用に1Dにする） output = np.concatenate([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールの設定をする。 ax3.set_xlim(0.0, 10.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' # モデルを定義 M, K, C = model() # 解析時間 dt = 1e-3 t_max = 100.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) var = np.concatenate([x0, v0]) # 外力（forceはFRF計算用） A = 1.0 f0 = 1.0 f1 = 100.0 k = (f1 - f0) / t_max force = A * np.sin(2 * np.pi * (f0 * t + (k / 2) * t ** 2)) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(M, K, C, A, k, f0)) # 結果を分離（odeint用の1D配列から物理量毎に分離） x = var.T[0:int(len(var.T) / 2)] v = var.T[int(len(var.T) / 2)::] amp, freq_axis = frf(force, x[-1], 1 / dt) # プロット plot(t, x[-1], force, amp, freq_axis) |
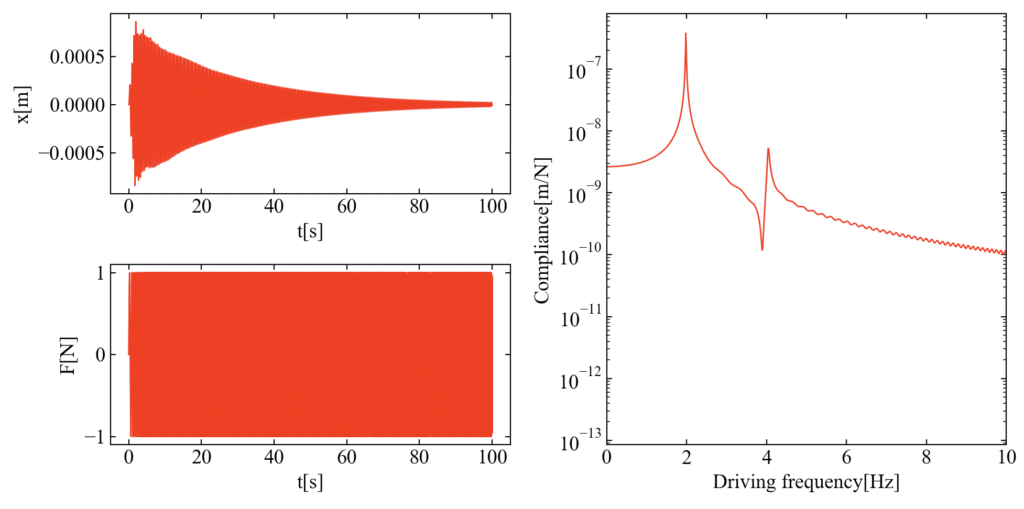
こちらが結果です。周波数応答関数の裾野がぐにゃぐにゃしているのは応答信号が減衰しきっていないためのリーケージエラーです。この応答曲線はサインスイープ加振だったとしても共振を過ぎると振幅が減衰しているので、本来は指数ウィンドウを使った上で周波数応答関数を処理するのですが、今回は面倒なので割愛（←）。
指数ウィンドウは過去にPythonで作ってみたことがあります。ご参考までに。
・Pythonで窓関数が無い場合は？指数窓を自作してみる!
N自由度減衰強制振動（片端固定）
次はN自由度振動系を表現してみましょう。まずは質点群片方の端部を固定した場合です。
N自由度になっても運動方程式自体は式（5）で表現されています。
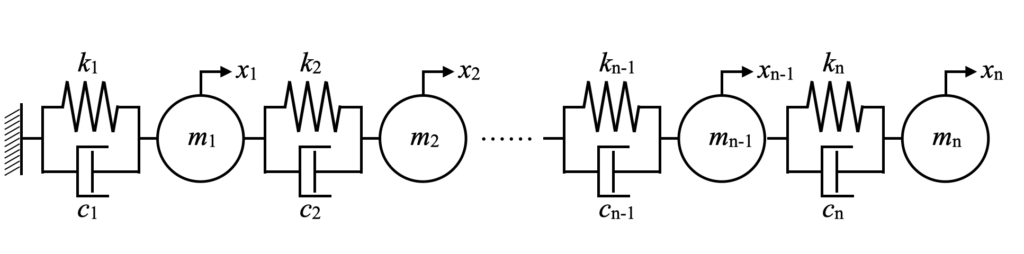
行列やベクトルの中身を可視化しながらN自由度に拡張すると、片端固定の場合の運動方程式は式（7）となります。
\[
\begin{bmatrix}
m_{1} &0 &0&\cdots&\cdots&0 \\
0 &m_{2}&0&\cdots &\cdots&0\\
0&0&\ddots&&&\vdots \\
\vdots&\vdots&&\ddots&&\vdots \\
\vdots &\vdots &&&m_{n-1}&0\\
0&0&\cdots &\cdots &0&m_{n}
\end{bmatrix}
\begin{bmatrix}
\ddot{x}_{1}\\
\ddot{x}_{2} \\
\vdots \\
\vdots \\
\ddot{x}_{n-1} \\
\ddot{x}_{n}
\end{bmatrix}
+
\begin{bmatrix}
c_{1}+c_{2} &-c_{2} &0&\cdots&\cdots&0 \\
-c_{2} &c_{2}+c_{3}&-c_{3}&0&\cdots &0\\
0&-c_{3}&\ddots&&&\vdots \\
0&0&&\ddots&&\vdots\\
\vdots &\vdots &&&c_{n-1}+c_n&-c_{n}\\
0&0&\cdots&\cdots &-c_{n} &c_{n}
\end{bmatrix}
\begin{bmatrix}
\dot{x}_{1}\\
\dot{x}_{2} \\
\vdots \\
\vdots \\
\dot{x}_{n-1} \\
\dot{x}_{n}
\end{bmatrix}
+
\begin{bmatrix}
k_{1}+k_{2} &-k_{2} &0&\cdots&\cdots&0 \\
-k_{2} &k_{2}+k_{3}&-k_{3}&0&\cdots &0\\
0&-k_{3}&\ddots&&&\vdots \\
0&0&&\ddots&&\vdots\\
\vdots &\vdots &&&k_{n-1}+k_n&-k_{n}\\
0&0&\cdots&\cdots &-k_{n} &k_{n}
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2} \\
\vdots \\
\vdots \\
x_{n-1} \\
x_{n}
\end{bmatrix}
=
\begin{bmatrix}
f_{1}\\
f_{2}\\
\vdots \\
\vdots \\
f_{n-1}\\
f_{n}\\
\end{bmatrix}
\tag{7}
\]
N自由度の場合、コードの中に長い行列を書くのが非常に煩わしいと感じます。
ここでは表計算ソフトで質量・剛性・減衰をcsvファイルとして作成するパターンで書いた以下のコードを使ってシミュレーションを行います（もちろん2自由度の時のようにコードに直接書いても問題ありません）。
csvファイルをダウンロードできるようにしておきますので、検証でお使いください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint import pandas as pd def generate_matrix(filename): ''' MCK行列を作成する(片端固定) ''' # ファイルを読む df = pd.read_csv(filename, encoding='SHIFT-JIS') # 質量と剛性のリストを取り出す m = df['m'] k = df['k'] c = df['c'] # フリーフリーの場合の剛性行列を生成する K_all = np.zeros([len(k) + 1, len(k) + 1]) for i in range(len(k)): # 単一ばね要素として剛性行列を定義する K = np.array([[k[i], -k[i]], [-k[i], k[i]]]) # iにより位置をシフトさせながらKを重畳する K_all[i:2 + i, i:2 + i] += K # print('i=',i, '\nK=\n', K_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） K_all = np.delete(K_all, 0, axis=0) K_all = np.delete(K_all, 0, axis=1) # フリーフリーの場合の減衰行列を生成する C_all = np.zeros([len(c) + 1, len(c) + 1]) for i in range(len(c)): # 単一ダッシュポット要素として減衰行列を定義する C = np.array([[c[i], -c[i]], [-c[i], c[i]]]) # iにより位置をシフトさせながらKを重畳する C_all[i:2 + i, i:2 + i] += C # print('i=',i, '\nC=\n', C_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） C_all = np.delete(C_all, 0, axis=0) C_all = np.delete(C_all, 0, axis=1) # 質量行列を生成する M_all = np.diag(m) return M_all, K_all, C_all def f(var, t, M, K, C, A, start, end): ''' Harmonic oscillator ''' # 質量行列の逆行列 M_inv = np.linalg.inv(M) # 外力 F = np.zeros(len(M)) # インパルス外力を計算 if (t >= start) & (t <= end): force = A else: force = 0.0 # 要素の最後に外力を設定 F[-1] = force # x, vに分離 x = var[0:int(len(var) / 2)] v = var[int(len(var) / 2)::] # 運動方程式 a = - (M_inv @ K) @ x - (M_inv @ C) @ v + (M_inv @ F) # 結果を平坦化（odeint用に1Dにする） output = np.concatenate([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールの設定をする。 ax3.set_xlim(0.0, 10.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' # モデルを定義 M, K, C = generate_matrix('ndof-system-cantilever.csv') # 解析時間 dt = 1e-3 t_max = 500.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) var = np.concatenate([x0, v0]) # 外力（インパルス加振）を計算 force = np.zeros_like(t) A = 1.0 start = 0.0 end = 0.001 force = np.where((t >= start) & (t <= end), A, 0) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(M, K, C, A, start, end)) # 結果を分離（odeint用の1D配列から物理量毎に分離） x = var.T[0:int(len(var.T) / 2)] v = var.T[int(len(var.T) / 2)::] amp, freq_axis = frf(force, x[-1], 1 / dt) # プロット plot(t, x[-1], force, amp, freq_axis) |
適当に自由度を設定し、例題のファイルは19自由度となっていました。コードを実行すると以下の結果が得られます。ピークがたくさんありますが、最初のピークが最も大きい結果でした。
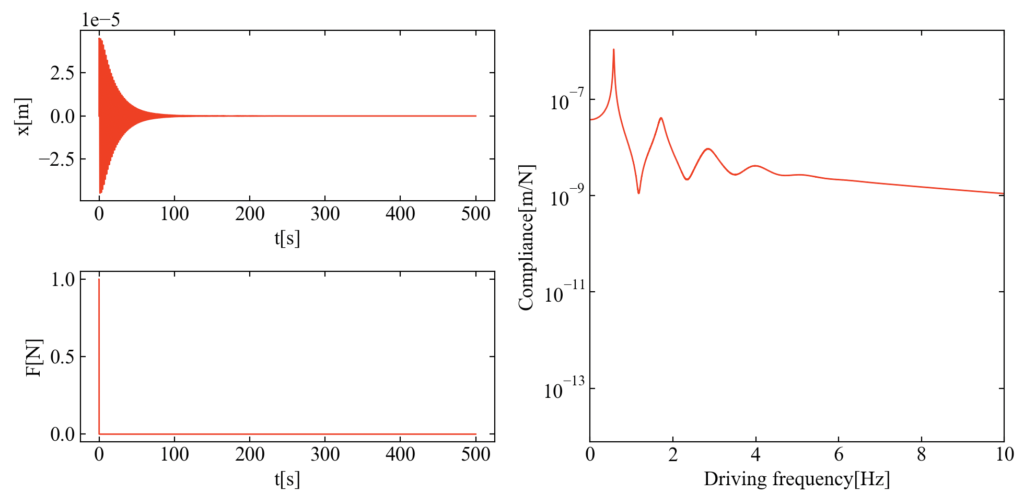
N自由度の質点挙動をアニメーションで確認する方法
これまでは任意質点1つだけの時間波形や周波数応答関数をプロットしていましたが、それとは別に全体の挙動を確認するコードも書いてみました。
plot_animation()という関数を作成し、interval（間引き数）とend_time（終了時間：シミュレーション上でアニメーションを打ち切る時間）を設定しました。
シミュレーション結果xやvは始めから全ての質点に関する全時間データが入っていますので、それをforループで呼び出してプロットしているだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint import pandas as pd from PIL import Image import os import glob def generate_matrix(filename): ''' MCK行列を作成する(片端固定) ''' # ファイルを読む df = pd.read_csv(filename, encoding='SHIFT-JIS') # 質量と剛性のリストを取り出す m = df['m'] k = df['k'] c = df['c'] # フリーフリーの場合の剛性行列を生成する K_all = np.zeros([len(k) + 1, len(k) + 1]) for i in range(len(k)): # 単一ばね要素として剛性行列を定義する K = np.array([[k[i], -k[i]], [-k[i], k[i]]]) # iにより位置をシフトさせながらKを重畳する K_all[i:2 + i, i:2 + i] += K # print('i=',i, '\nK=\n', K_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） K_all = np.delete(K_all, 0, axis=0) K_all = np.delete(K_all, 0, axis=1) # フリーフリーの場合の減衰行列を生成する C_all = np.zeros([len(c) + 1, len(c) + 1]) for i in range(len(c)): # 単一ダッシュポット要素として減衰行列を定義する C = np.array([[c[i], -c[i]], [-c[i], c[i]]]) # iにより位置をシフトさせながらKを重畳する C_all[i:2 + i, i:2 + i] += C # print('i=',i, '\nC=\n', C_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） C_all = np.delete(C_all, 0, axis=0) C_all = np.delete(C_all, 0, axis=1) # 質量行列を生成する M_all = np.diag(m) return M_all, K_all, C_all def f(var, t, M, K, C, A, start, end): ''' Harmonic oscillator ''' # 質量行列の逆行列 M_inv = np.linalg.inv(M) # 外力 F = np.zeros(len(M)) # インパルス外力を計算 if (t >= start) & (t <= end): force = A else: force = 0.0 # 要素の最後に外力を設定 F[-1] = force # x, vに分離 x = var[0:int(len(var) / 2)] v = var[int(len(var) / 2)::] # 運動方程式 a = - (M_inv @ K) @ x - (M_inv @ C) @ v + (M_inv @ F) # 結果を平坦化（odeint用に1Dにする） output = np.concatenate([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールの設定をする。 ax3.set_xlim(0.0, 10.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルのフルパスからファイル名と拡張子を抽出 imgs = [] for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) return def plot_animation(t, x, interval, end_time, dir_name): ''' プロットをアニメーションにする ''' index = 0 for i in range(len(x)): print('i=', i, 't=', np.round(t[i], 4), '[s]') if t[i] > end_time: break if i % interval == 0: # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Degree of Freedom') ax1.set_ylabel('x[m]') # スケールの設定をする。 ax1.set_xlim(0.0, len(x[i]) + 1) ax1.set_ylim(np.min(x) * 1.1, np.max(x) * 1.1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 dof = np.arange(1, len(x[i]) + 1, 1) ax1.plot(dof, x[i], label='Displacement', lw=1, color='red', marker='o') ax1.text(0.5, np.max(x) * 0.9, 't=' + str(np.round(t[i], 4)) + '[s]') # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 if os.path.exists(dir_name): pass else: os.mkdir(dir_name) # 画像保存パスを準備 path = os.path.join(*[dir_name, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() index += 1 if __name__ == '__main__': ''' メイン処理 ''' # モデルを定義 M, K, C = generate_matrix('ndof-system-cantilever.csv') # 解析時間 dt = 1e-3 t_max = 500.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) var = np.concatenate([x0, v0]) # 外力（インパルス加振）を計算 force = np.zeros_like(t) A = 1.0 start = 0.0 end = 0.001 force = np.where((t >= start) & (t <= end), A, 0) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(M, K, C, A, start, end)) # 結果を分離（odeint用の1D配列から物理量毎に分離） x = var.T[0:int(len(var.T) / 2)] v = var.T[int(len(var.T) / 2)::] amp, freq_axis = frf(force, x[-1], 1 / dt) # プロット plot(t, x[-1], force, amp, freq_axis) # プロットをアニメーションにする interval = 100 end_time = 20 dir_name = 'cantilever' plot_animation(t, x.T, interval, end_time, dir_name) # GIF動画を作成する create_gif(dir_name, 'cantilever.gif') |
このコードを実行すると、まず始めに先ほどの時間波形と周波数応答関数が表示され、それを閉じるとアニメーション作成が開始されます。指定した時間でループが終了するとcantilever.gifというGIF動画が作成されます。
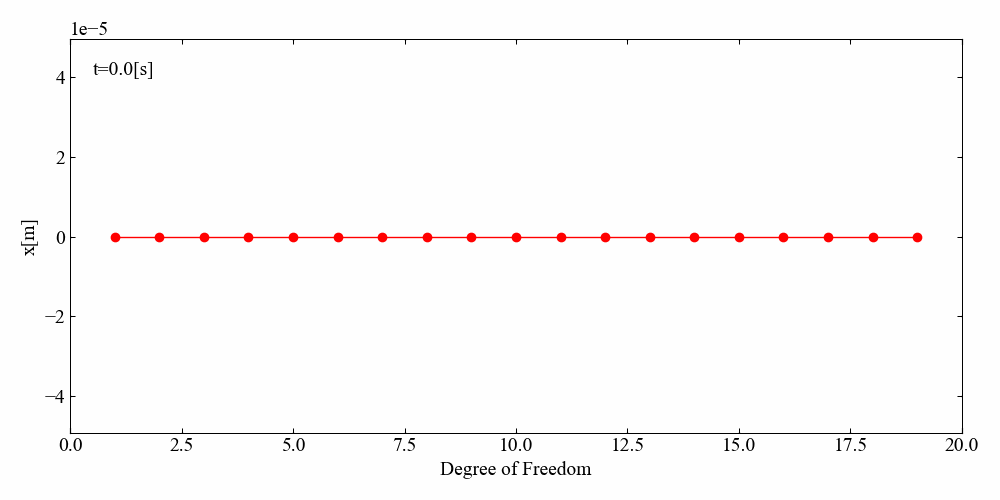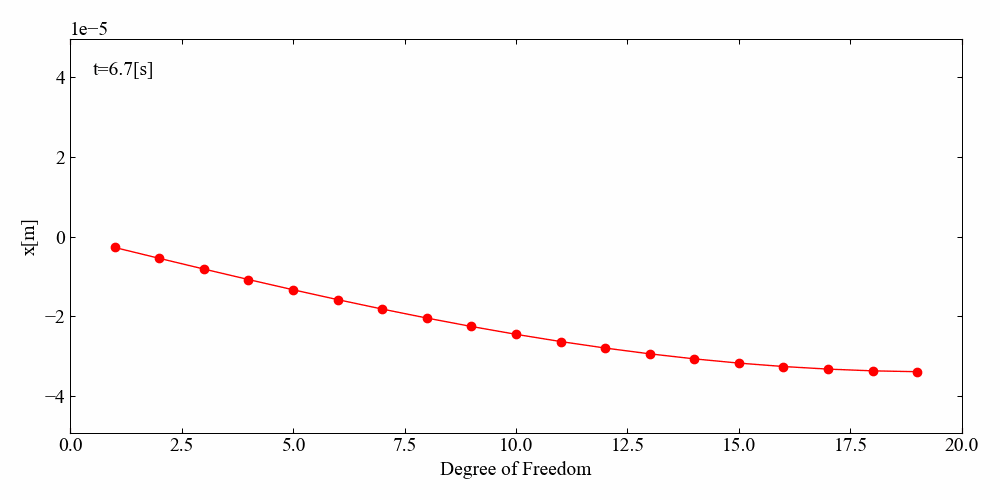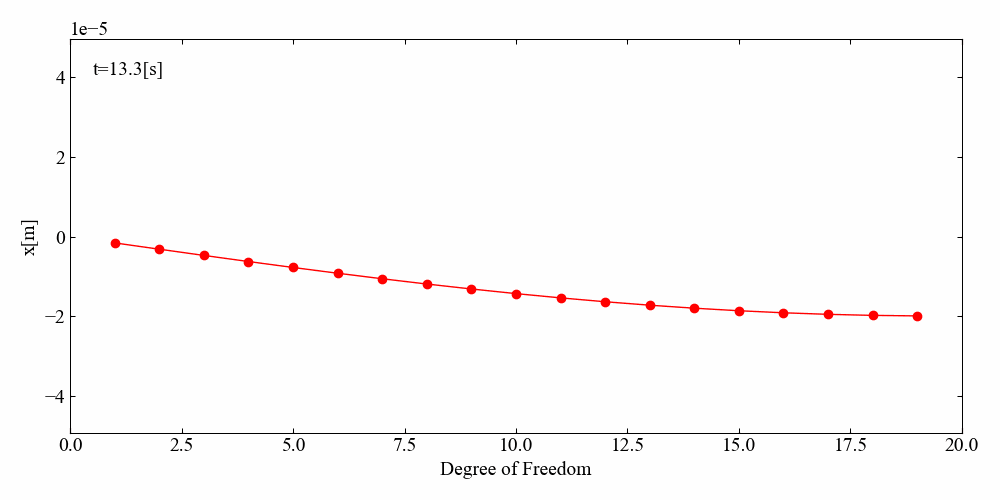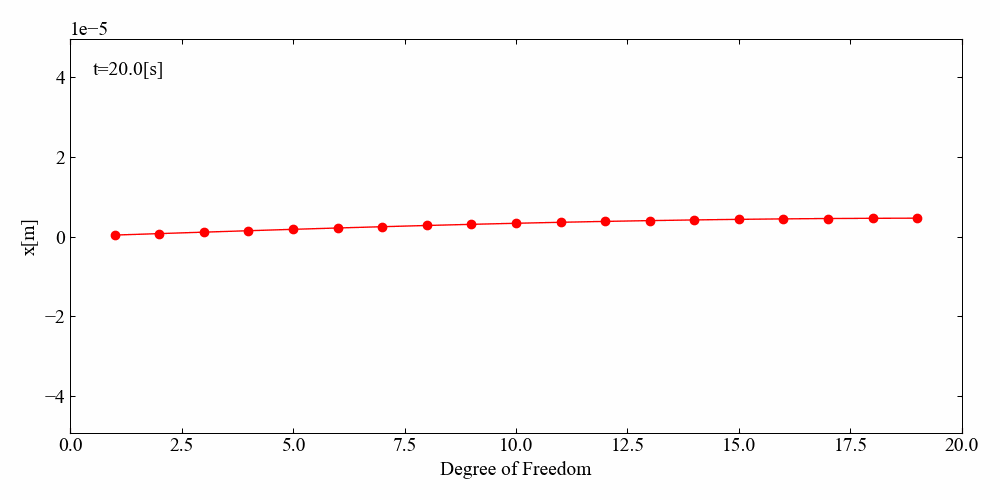
びよんびよんしています。
N自由度減衰強制振動（両端固定）
中央加振
次は先ほどのN自由度振動系において、両端固定の場合を検討します。
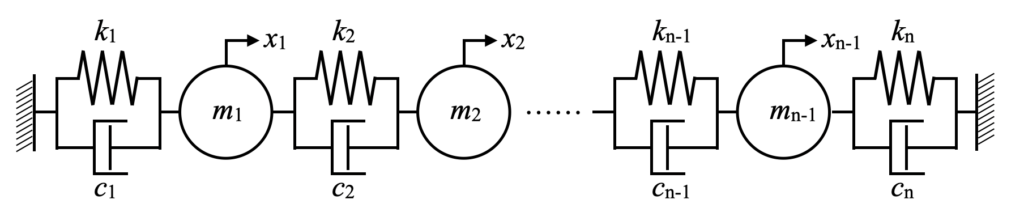
片端固定の運動方程式が書けていれば両端固定の運動方程式を導出するのは簡単です。
下図のように固定したい自由度の行と列を削除することで固定（拘束）を表現できます。
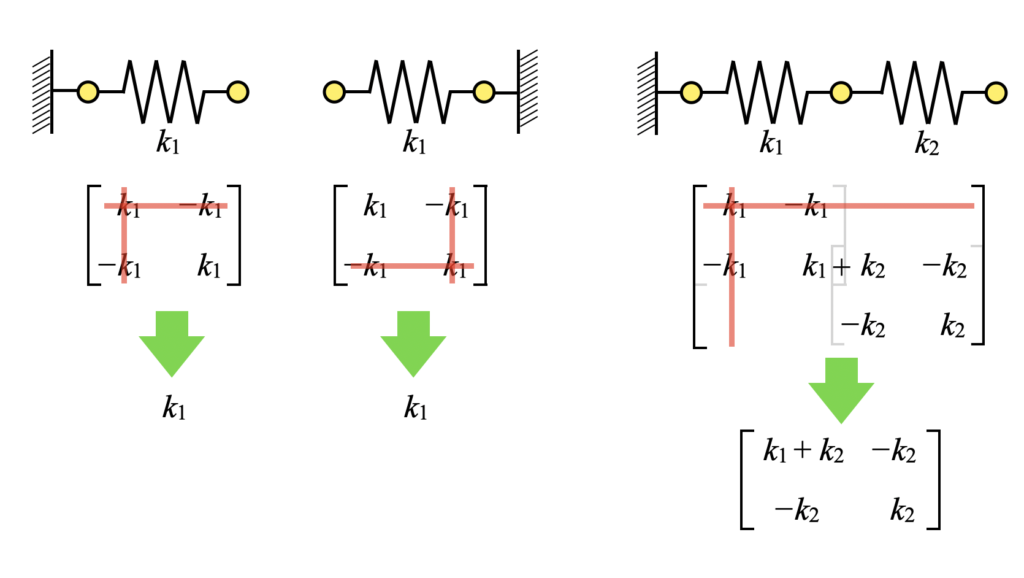
そのため両端固定N自由度振動系の運動方程式は式（7）を少し変形させて式（8）となります。
\[
\begin{bmatrix}
m_{1} &0 &0&\cdots&\cdots&0 \\
0 &m_{2}&0&\cdots &\cdots&0\\
0&0&\ddots&&&\vdots \\
\vdots&\vdots&&\ddots&&\vdots \\
\vdots &\vdots &&&\ddots&0\\
0&0&\cdots &\cdots &0&m_{n-1}
\end{bmatrix}
\begin{bmatrix}
\ddot{x}_{1}\\
\ddot{x}_{2} \\
\vdots \\
\vdots \\
\vdots \\
\ddot{x}_{n-1}
\end{bmatrix}
+
\begin{bmatrix}
c_{1}+c_{2} &-c_{2} &0&\cdots&\cdots&0 \\
-c_{2} &c_{2}+c_{3}&-c_{3}&0&\cdots &0\\
0&-c_{3}&\ddots&&&\vdots \\
0&0&&\ddots&&\vdots\\
\vdots &\vdots &&&\ddots&-c_{n-1}\\
0&0&\cdots&\cdots &-c_{n-1} &c_{n-1}+c_{n}
\end{bmatrix}
\begin{bmatrix}
\dot{x}_{1}\\
\dot{x}_{2} \\
\vdots \\
\vdots \\
\vdots \\
\dot{x}_{n-1}
\end{bmatrix}
+
\begin{bmatrix}
k_{1}+k_{2} &-k_{2} &0&\cdots&\cdots&0 \\
-k_{2} &k_{2}+k_{3}&-k_{3}&0&\cdots &0\\
0&-k_{3}&\ddots&&&\vdots \\
0&0&&\ddots&&\vdots\\
\vdots &\vdots &&&\ddots&-k_{n-1}\\
0&0&\cdots&\cdots &-k_{n-1} &k_{n-1}+k_{n}
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2} \\
\vdots \\
\vdots \\
\vdots \\
x_{n-1}
\end{bmatrix}
=
\begin{bmatrix}
f_{1} \\
f_{2} \\
\vdots \\
\vdots \\
\vdots \\
f_{n-1}\\
\end{bmatrix}
\tag{8}
\]
コード上ではgenerate_matrix()関数の中で、np.delete()をK_all, C_all, M_allに対して追加して式変形を表現しました。また両端支持の振動系なのでインパルス加振を与える位置はf()関数の中でforce_posを設定し、ちょうど中間の質点に印加するようにしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint import pandas as pd from PIL import Image import os import glob def generate_matrix(filename): ''' MCK行列を作成する(両端固定) ''' # ファイルを読む df = pd.read_csv(filename, encoding='SHIFT-JIS') # 質量と剛性のリストを取り出す m = df['m'] k = df['k'] c = df['c'] # フリーフリーの場合の剛性行列を生成する K_all = np.zeros([len(k) + 1, len(k) + 1]) for i in range(len(k)): # 単一ばね要素として剛性行列を定義する K = np.array([[k[i], -k[i]], [-k[i], k[i]]]) # iにより位置をシフトさせながらKを重畳する K_all[i:2 + i, i:2 + i] += K # print('i=',i, '\nK=\n', K_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） K_all = np.delete(K_all, 0, axis=0) K_all = np.delete(K_all, 0, axis=1) K_all = np.delete(K_all, -1, axis=0) K_all = np.delete(K_all, -1, axis=1) # フリーフリーの場合の減衰行列を生成する C_all = np.zeros([len(c) + 1, len(c) + 1]) for i in range(len(c)): # 単一ダッシュポット要素として減衰行列を定義する C = np.array([[c[i], -c[i]], [-c[i], c[i]]]) # iにより位置をシフトさせながらKを重畳する C_all[i:2 + i, i:2 + i] += C # print('i=',i, '\nC=\n', C_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） C_all = np.delete(C_all, 0, axis=0) C_all = np.delete(C_all, 0, axis=1) C_all = np.delete(C_all, -1, axis=0) C_all = np.delete(C_all, -1, axis=1) # 質量行列を生成する M_all = np.diag(m) M_all = np.delete(M_all, -1, axis=0) M_all = np.delete(M_all, -1, axis=1) return M_all, K_all, C_all def f(var, t, M, K, C, A, start, end): ''' Harmonic oscillator ''' # 質量行列の逆行列 M_inv = np.linalg.inv(M) # 外力 F = np.zeros(len(M)) # インパルス外力を計算 if (t >= start) & (t <= end): force = A else: force = 0.0 # 要素の中間に外力を設定 force_pos = int(len(M) / 2) F[force_pos] = force # x, vに分離 x = var[0:int(len(var) / 2)] v = var[int(len(var) / 2)::] # 運動方程式 a = - (M_inv @ K) @ x - (M_inv @ C) @ v + (M_inv @ F) # 結果を平坦化（odeint用に1Dにする） output = np.concatenate([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールの設定をする。 ax3.set_xlim(0.0, 10.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルのフルパスからファイル名と拡張子を抽出 imgs = [] for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) return def plot_animation(t, x, interval, end_time, dir_name): ''' プロットをアニメーションにする ''' index = 0 for i in range(len(x)): print('i=', i, 't=', np.round(t[i], 4), '[s]') if t[i] > end_time: break if i % interval == 0: # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Degree of Freedom') ax1.set_ylabel('x[m]') # スケールの設定をする。 ax1.set_xlim(0.0, len(x[i]) + 1) ax1.set_ylim(np.min(x) * 1.1, np.max(x) * 1.1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 dof = np.arange(1, len(x[i]) + 1, 1) ax1.plot(dof, x[i], label='Displacement', lw=1, color='red', marker='o') ax1.text(0.5, np.max(x) * 0.9, 't=' + str(np.round(t[i], 4)) + '[s]') # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 if os.path.exists(dir_name): pass else: os.mkdir(dir_name) # 画像保存パスを準備 path = os.path.join(*[dir_name, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() index += 1 if __name__ == '__main__': ''' メイン処理 ''' # モデルを定義 M, K, C = generate_matrix('ndof-system-cantilever.csv') # 解析時間 dt = 1e-3 t_max = 500.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) var = np.concatenate([x0, v0]) # 外力（インパルス加振）を計算 force = np.zeros_like(t) A = 1.0 start = 0.0 end = 0.001 force = np.where((t >= start) & (t <= end), A, 0) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(M, K, C, A, start, end)) # 結果を分離（odeint用の1D配列から物理量毎に分離） x = var.T[0:int(len(var.T) / 2)] v = var.T[int(len(var.T) / 2)::] amp, freq_axis = frf(force, x[-1], 1 / dt) # プロット plot(t, x[-1], force, amp, freq_axis) # プロットをアニメーションにする interval = 100 end_time = 20 dir_name = 'double-supported-beam' plot_animation(t, x.T, interval, end_time, dir_name) # GIF動画を作成する create_gif(dir_name, 'double-supported-beam.gif') |
時間波形と周波数応答関数を示します。先ほどとちょっとピークの形が変わりましたね。
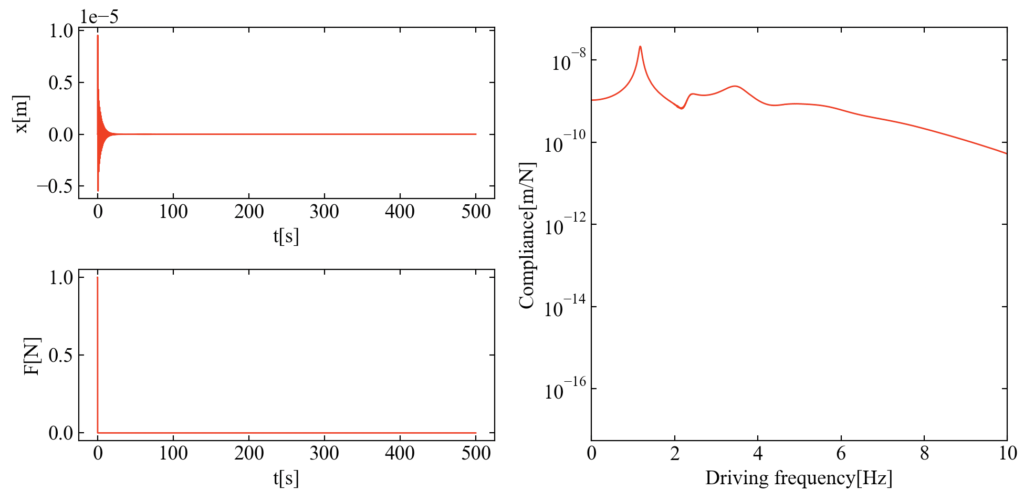
コードを実行すると動画はdouble-supported-beam.gifが作成されます。
動画で可視化してみると一目瞭然です。運動方程式を少し変えただけで両端の変位が小さくなりました。当たり前の結果ですが面白いですね。
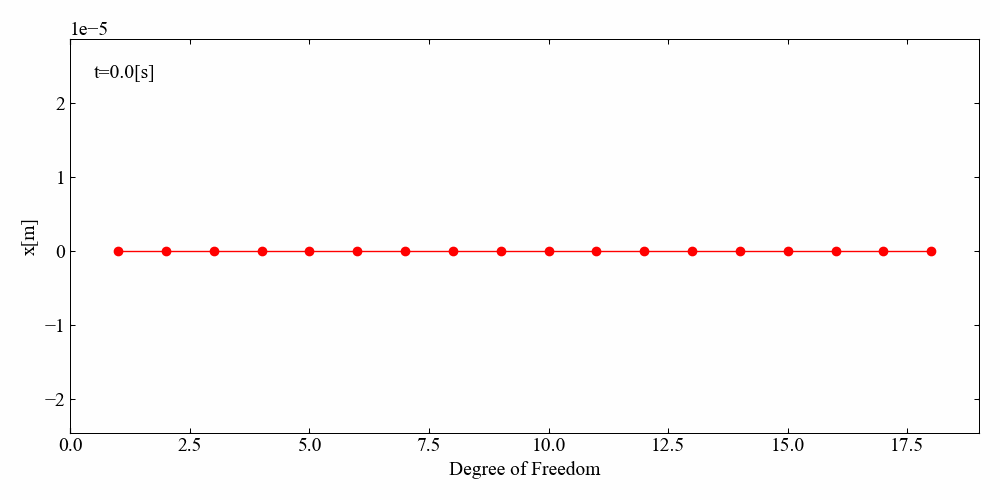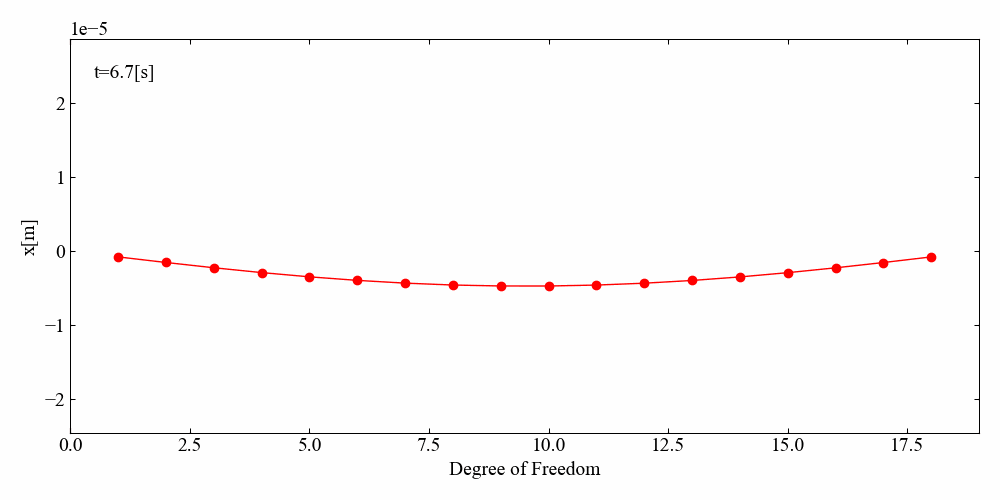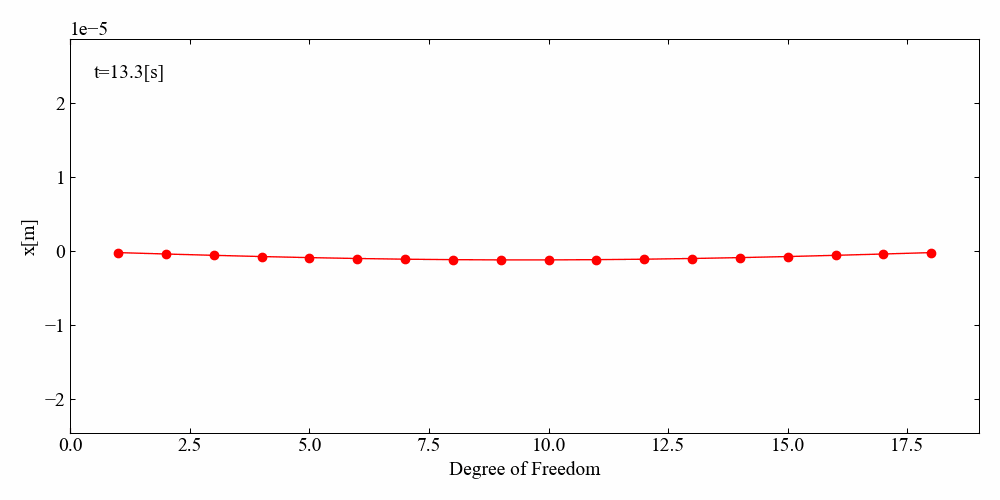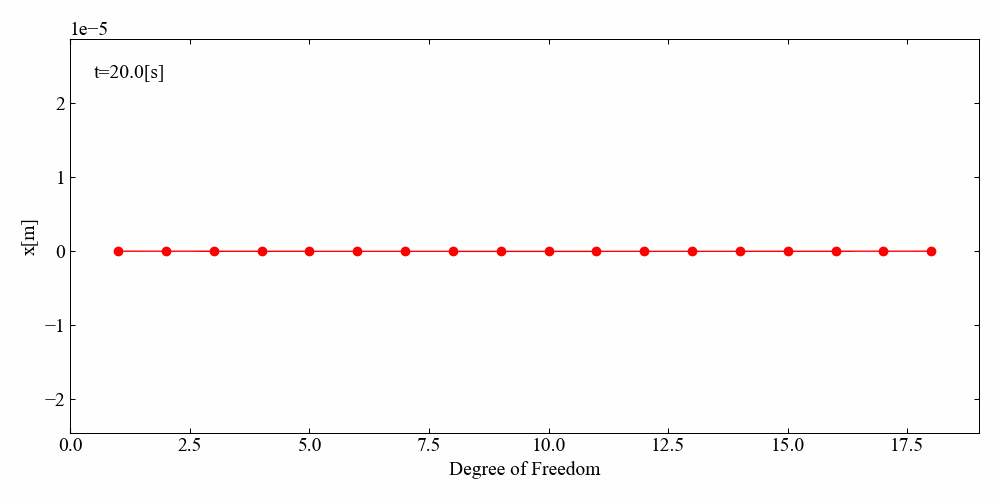
びよんびよんしています！
端部加振
f()関数内のforce_posを以下の内容に修正して、加振点を左端にしてみましょう。
|
1 2 |
# 要素の端部に外力を設定 force_pos = 0 |
動画のみ紹介しますが、左端から波が伝わっていく様子がわかりました。
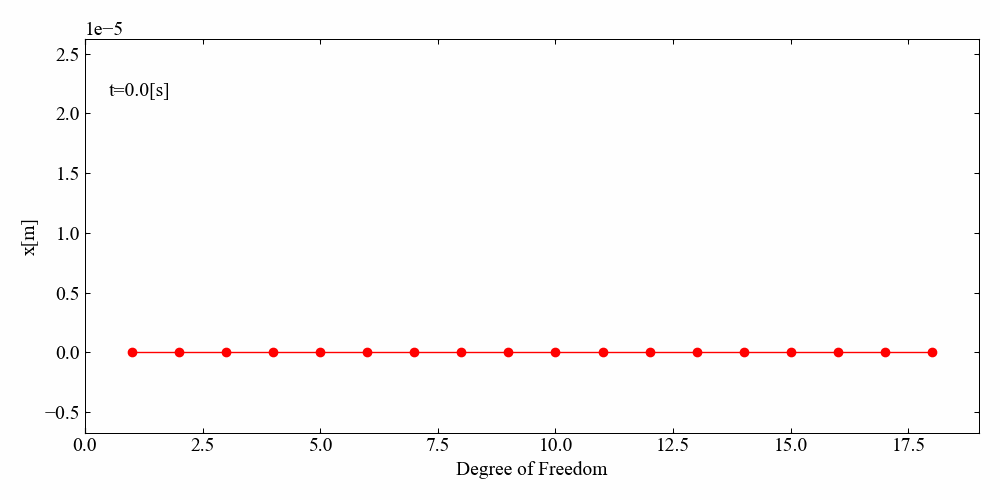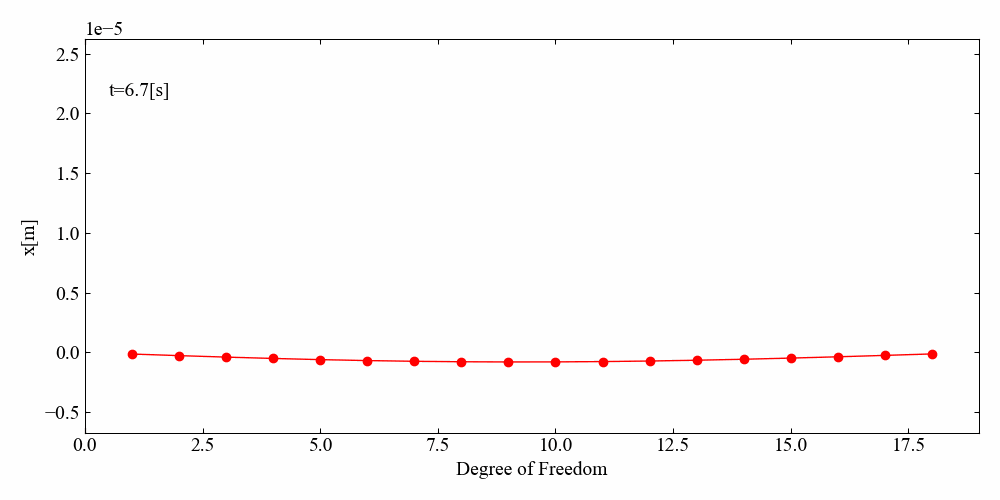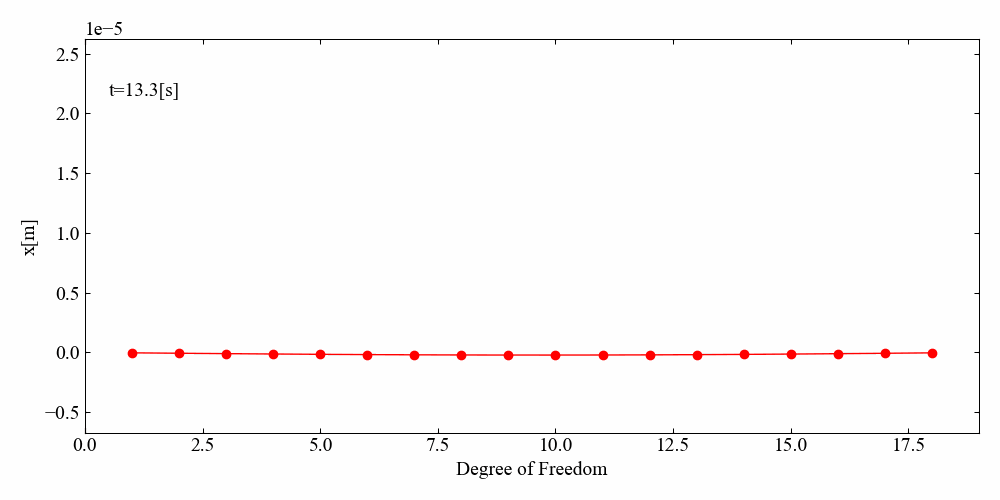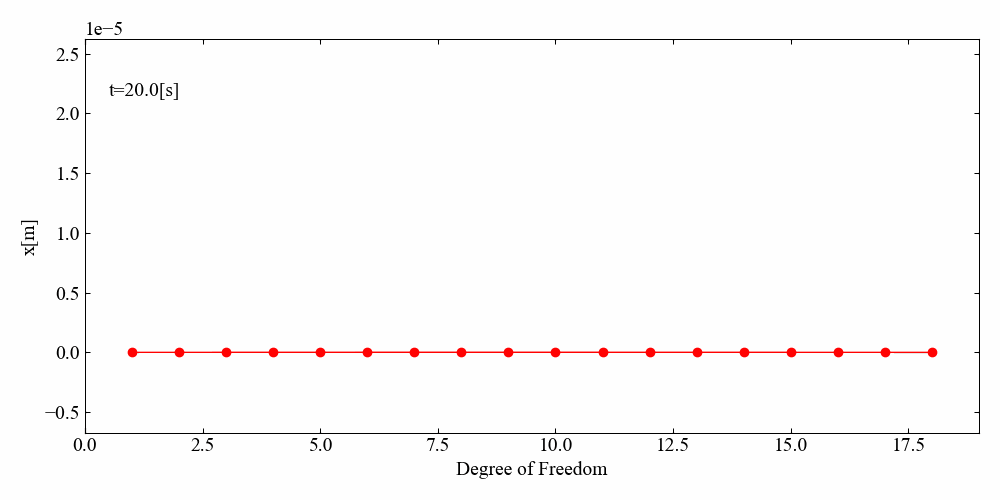
端部サインスイープ加振
せっかくなのでサインスイープ加振も試してみましょう。既に紹介したコードを組み合わせるだけですが、コピペで動作できるようにした方が便利かもしれないので全コードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint import pandas as pd from PIL import Image import os import glob def generate_matrix(filename): ''' MCK行列を作成する(両端固定) ''' # ファイルを読む df = pd.read_csv(filename, encoding='SHIFT-JIS') # 質量と剛性のリストを取り出す m = df['m'] k = df['k'] c = df['c'] # フリーフリーの場合の剛性行列を生成する K_all = np.zeros([len(k) + 1, len(k) + 1]) for i in range(len(k)): # 単一ばね要素として剛性行列を定義する K = np.array([[k[i], -k[i]], [-k[i], k[i]]]) # iにより位置をシフトさせながらKを重畳する K_all[i:2 + i, i:2 + i] += K # print('i=',i, '\nK=\n', K_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） K_all = np.delete(K_all, 0, axis=0) K_all = np.delete(K_all, 0, axis=1) K_all = np.delete(K_all, -1, axis=0) K_all = np.delete(K_all, -1, axis=1) # フリーフリーの場合の減衰行列を生成する C_all = np.zeros([len(c) + 1, len(c) + 1]) for i in range(len(c)): # 単一ダッシュポット要素として減衰行列を定義する C = np.array([[c[i], -c[i]], [-c[i], c[i]]]) # iにより位置をシフトさせながらKを重畳する C_all[i:2 + i, i:2 + i] += C # print('i=',i, '\nC=\n', C_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） C_all = np.delete(C_all, 0, axis=0) C_all = np.delete(C_all, 0, axis=1) C_all = np.delete(C_all, -1, axis=0) C_all = np.delete(C_all, -1, axis=1) # 質量行列を生成する M_all = np.diag(m) M_all = np.delete(M_all, -1, axis=0) M_all = np.delete(M_all, -1, axis=1) return M_all, K_all, C_all def f(var, t, M, K, C, A, alpha, f0): ''' Harmonic oscillator ''' # 質量行列の逆行列 M_inv = np.linalg.inv(M) # 外力 F = np.zeros(len(M)) # 外力を計算 force = A * np.sin(2 * np.pi * (f0 * t + (alpha / 2) * t ** 2)) # 要素の端部に外力を設定 force_pos = 0 F[force_pos] = force # x, vに分離 x = var[0:int(len(var) / 2)] v = var[int(len(var) / 2)::] # 運動方程式 a = - (M_inv @ K) @ x - (M_inv @ C) @ v + (M_inv @ F) # 結果を平坦化（odeint用に1Dにする） output = np.concatenate([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールの設定をする。 ax3.set_xlim(0.0, 10.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルのフルパスからファイル名と拡張子を抽出 imgs = [] for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) return def plot_animation(t, x, interval, end_time, dir_name): ''' プロットをアニメーションにする ''' index = 0 for i in range(len(x)): print('i=', i, 't=', np.round(t[i], 4), '[s]') if t[i] > end_time: break if i % interval == 0: # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Degree of Freedom') ax1.set_ylabel('x[m]') # スケールの設定をする。 ax1.set_xlim(0.0, len(x[i]) + 1) ax1.set_ylim(np.min(x) * 1.1, np.max(x) * 1.1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 dof = np.arange(1, len(x[i]) + 1, 1) ax1.plot(dof, x[i], label='Displacement', lw=1, color='red', marker='o') ax1.text(0.5, np.max(x) * 0.9, 't=' + str(np.round(t[i], 4)) + '[s]') # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 if os.path.exists(dir_name): pass else: os.mkdir(dir_name) # 画像保存パスを準備 path = os.path.join(*[dir_name, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() index += 1 if __name__ == '__main__': ''' メイン処理 ''' # モデルを定義 M, K, C = generate_matrix('ndof-system-cantilever.csv') # 解析時間 dt = 1e-3 t_max = 50.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) var = np.concatenate([x0, v0]) # 外力（チャープ信号）を計算 f0 = 1 f1 = 50 A = 100.0 alpha = (f1 - f0) / t_max force = A * np.sin(2 * np.pi * (f0 * t + (alpha / 2) * t ** 2)) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(M, K, C, A, alpha, f0)) # 結果を分離（odeint用の1D配列から物理量毎に分離） x = var.T[0:int(len(var.T) / 2)] v = var.T[int(len(var.T) / 2)::] amp, freq_axis = frf(force, x[-1], 1 / dt) # プロット plot(t, x[-1], force, amp, freq_axis) # プロットをアニメーションにする interval = 20 end_time = 5 dir_name = 'double-supported-beam' plot_animation(t, x.T, interval, end_time, dir_name) # GIF動画を作成する create_gif(dir_name, 'double-supported-beam.gif') |
縄跳びのシミュレーションのようになりました。
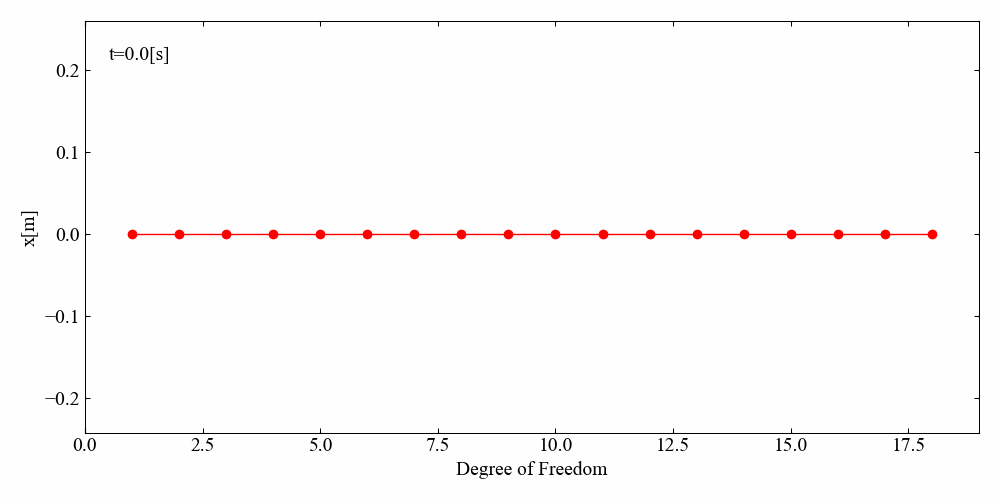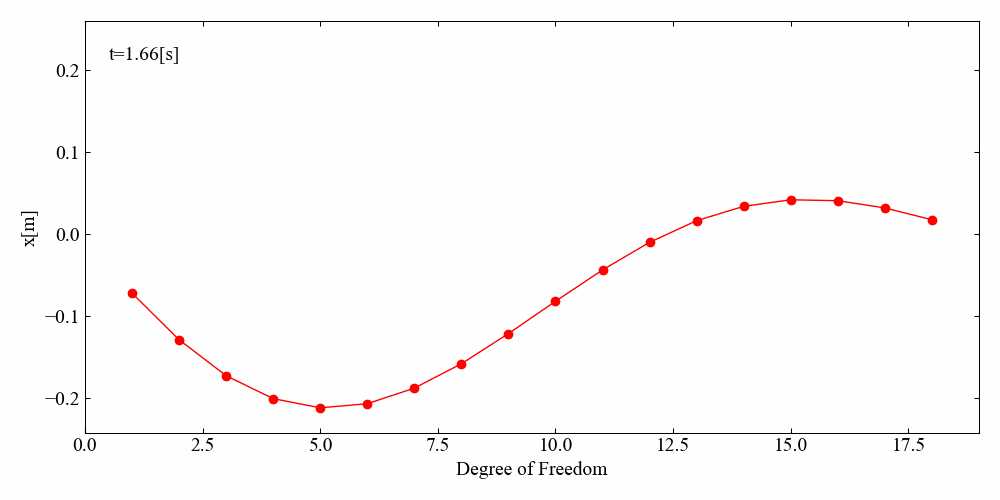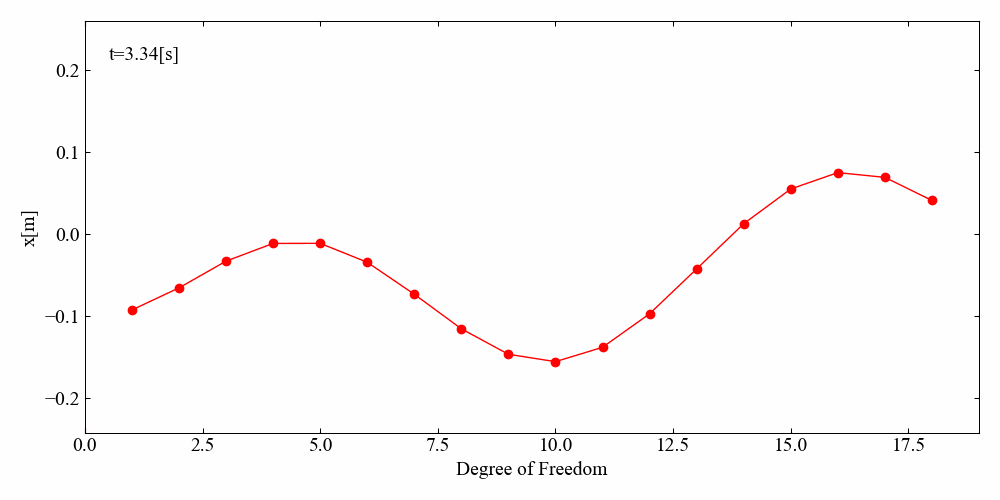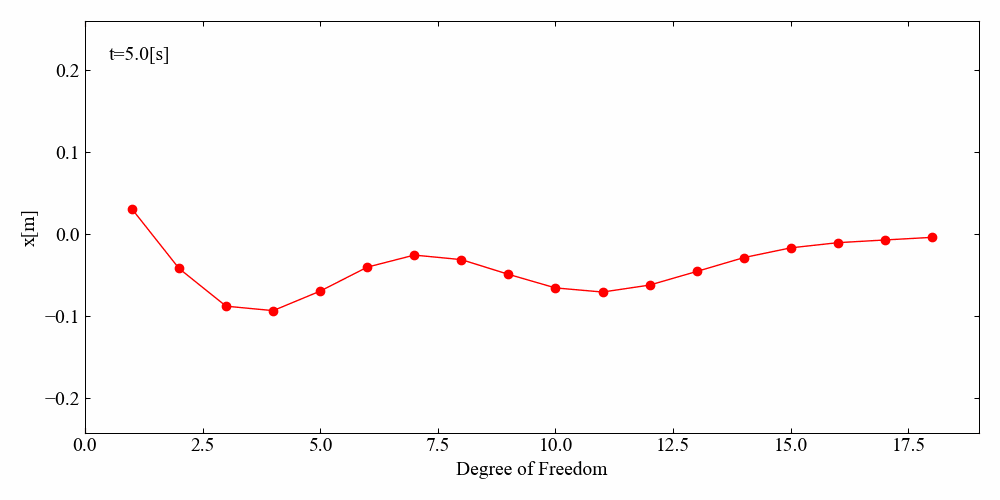
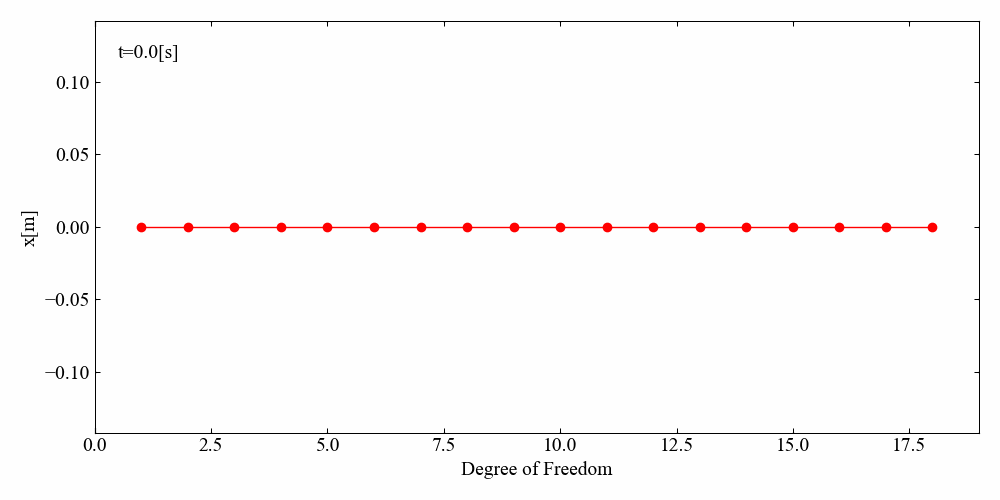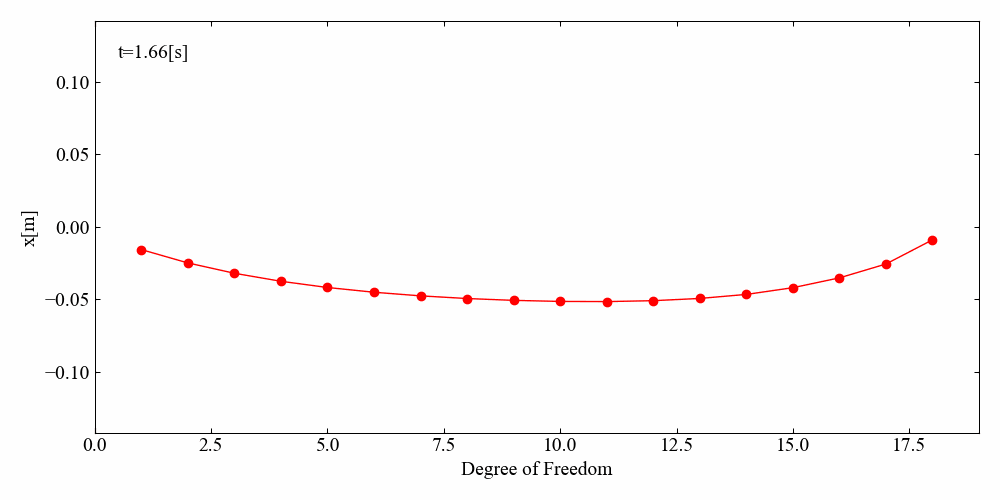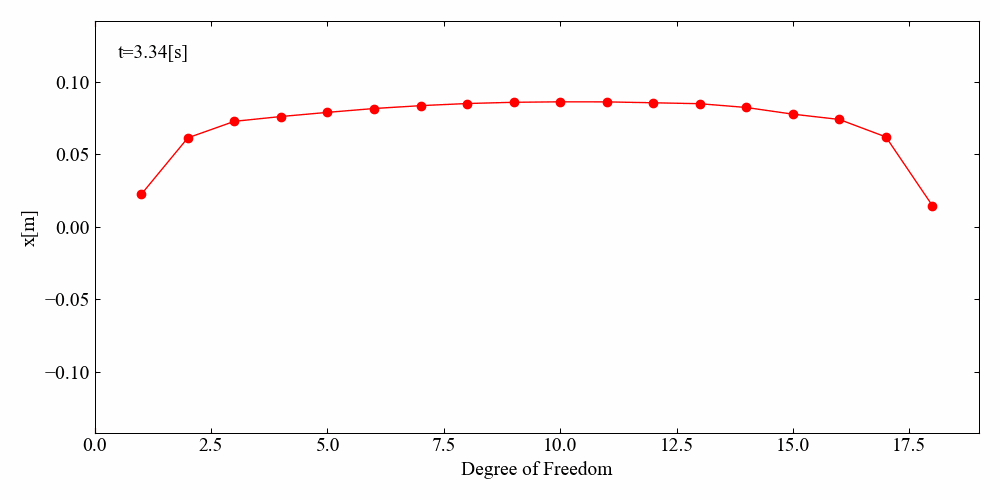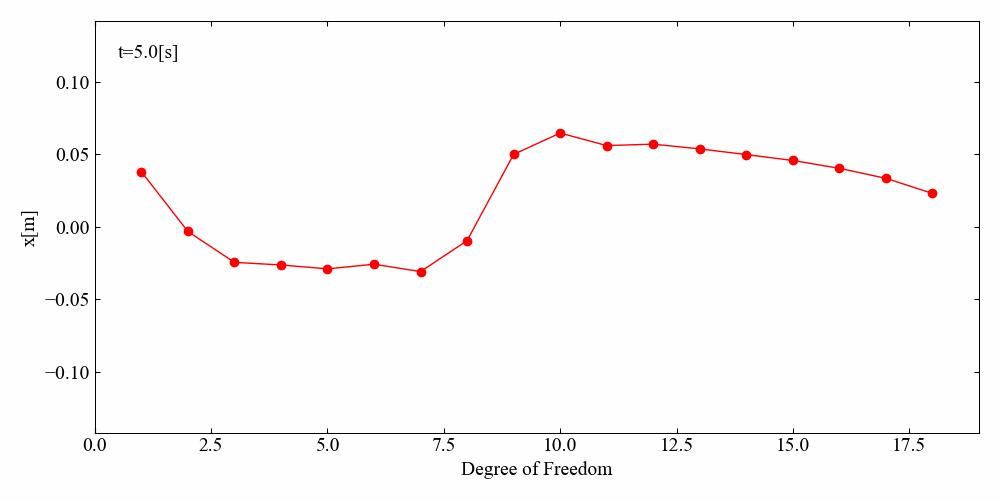
N自由度Duffing方程式の強制振動アニメーション
最後はN自由度Duffing方程式を可視化してみましょう。
Duffing方程式（式（9））は「PythonでDuffing振動子を解析してアトラクターを見る」の記事でアトラクターを確認しましたが、今回はN自由度ということで以下の式（10）と表現しました。
\[
\ddot{x} + \delta \dot{x} + \alpha x + \beta x^{3} = \gamma \cos(\omega t + \phi)
\tag{9}
\]
\[
\mathbf{M}\mathbf{\ddot{x}} + \mathbf{C}\mathbf{\dot{x}} + \mathbf{K_{\alpha}}\mathbf{x} + \mathbf{K_{\beta}}\mathbf{x}^{3} =\mathbf{F}
\tag{10}
\]
コード例を以下に示します。式（10）の3乗項にかかる係数は簡単に既存剛性行列を1000倍するだけにしました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint import pandas as pd from PIL import Image import os import glob def generate_matrix(filename): ''' MCK行列を作成する(両端固定) ''' # ファイルを読む df = pd.read_csv(filename, encoding='SHIFT-JIS') # 質量と剛性のリストを取り出す m = df['m'] k = df['k'] c = df['c'] # フリーフリーの場合の剛性行列を生成する K_all = np.zeros([len(k) + 1, len(k) + 1]) for i in range(len(k)): # 単一ばね要素として剛性行列を定義する K = np.array([[k[i], -k[i]], [-k[i], k[i]]]) # iにより位置をシフトさせながらKを重畳する K_all[i:2 + i, i:2 + i] += K # print('i=',i, '\nK=\n', K_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） K_all = np.delete(K_all, 0, axis=0) K_all = np.delete(K_all, 0, axis=1) K_all = np.delete(K_all, -1, axis=0) K_all = np.delete(K_all, -1, axis=1) # フリーフリーの場合の減衰行列を生成する C_all = np.zeros([len(c) + 1, len(c) + 1]) for i in range(len(c)): # 単一ダッシュポット要素として減衰行列を定義する C = np.array([[c[i], -c[i]], [-c[i], c[i]]]) # iにより位置をシフトさせながらKを重畳する C_all[i:2 + i, i:2 + i] += C # print('i=',i, '\nC=\n', C_all) # デバッグ用 # 拘束を反映させる（第一節点の固定） C_all = np.delete(C_all, 0, axis=0) C_all = np.delete(C_all, 0, axis=1) C_all = np.delete(C_all, -1, axis=0) C_all = np.delete(C_all, -1, axis=1) # 質量行列を生成する M_all = np.diag(m) M_all = np.delete(M_all, -1, axis=0) M_all = np.delete(M_all, -1, axis=1) return M_all, K_all, C_all def f(var, t, M, K, C, A, alpha, f0): ''' Duffing oscillator ''' # 質量行列の逆行列 M_inv = np.linalg.inv(M) # 外力 F = np.zeros(len(M)) # 外力を計算 force = A * np.sin(2 * np.pi * (f0 * t + (alpha / 2) * t ** 2)) # 要素の端部に外力を設定 force_pos = 0 F[force_pos] = force # x, vに分離 x = var[0:int(len(var) / 2)] v = var[int(len(var) / 2)::] # 運動方程式(今回は単純に3乗項の剛性行列を1000倍しただけ) a = - (M_inv @ K) @ x - (M_inv @ (1000 * K)) @ x ** 3 - (M_inv @ C) @ v + (M_inv @ F) # 結果を平坦化（odeint用に1Dにする） output = np.concatenate([v, a]) return output def frf(input, output, samplerate): ''' 周波数応答関数(FRF) ''' # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input) fft_o = fftpack.fft(output) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input) / 2) phase = np.arctan2(h_io.imag, h_io.real) phase = np.degrees(phase) freq = np.linspace(0, samplerate, len(input)) return amp, freq def plot(t, x, force, amp, freq): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('F[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールの設定をする。 ax3.set_xlim(0.0, 10.0) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, force, label='Force', lw=1, color='red') ax3.plot(freq, amp, label='FRF', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルのフルパスからファイル名と拡張子を抽出 imgs = [] for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) return def plot_animation(t, x, interval, end_time, dir_name): ''' プロットをアニメーションにする ''' index = 0 for i in range(len(x)): print('i=', i, 't=', np.round(t[i], 4), '[s]') if t[i] > end_time: break if i % interval == 0: # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Degree of Freedom') ax1.set_ylabel('x[m]') # スケールの設定をする。 ax1.set_xlim(0.0, len(x[i]) + 1) ax1.set_ylim(np.min(x) * 1.1, np.max(x) * 1.1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 dof = np.arange(1, len(x[i]) + 1, 1) ax1.plot(dof, x[i], label='Displacement', lw=1, color='red', marker='o') ax1.text(0.5, np.max(x) * 0.9, 't=' + str(np.round(t[i], 4)) + '[s]') # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 if os.path.exists(dir_name): pass else: os.mkdir(dir_name) # 画像保存パスを準備 path = os.path.join(*[dir_name, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() index += 1 if __name__ == '__main__': ''' メイン処理 ''' # モデルを定義 M, K, C = generate_matrix('ndof-system-cantilever.csv') # 解析時間 dt = 1e-3 t_max = 50.0 t = np.arange(0.0, t_max, dt) # 初期条件 x0 = np.zeros(len(M)) v0 = np.zeros(len(M)) var = np.concatenate([x0, v0]) # 外力（チャープ信号）を計算 f0 = 1 f1 = 50 A = 100.0 alpha = (f1 - f0) / t_max force = A * np.sin(2 * np.pi * (f0 * t + (alpha / 2) * t ** 2)) # 微分方程式の近似解法（過渡応答） var = odeint(f, var, t, args=(M, K, C, A, alpha, f0)) # 結果を分離（odeint用の1D配列から物理量毎に分離） x = var.T[0:int(len(var.T) / 2)] v = var.T[int(len(var.T) / 2)::] amp, freq_axis = frf(force, x[-1], 1 / dt) # プロット plot(t, x[-1], force, amp, freq_axis) # プロットをアニメーションにする interval = 20 end_time = 5 dir_name = 'double-supported-beam' plot_animation(t, x.T, interval, end_time, dir_name) # GIF動画を作成する create_gif(dir_name, 'double-supported-beam.gif') |
こちらが結果です…がちょっとカクカクした挙動になりました。非線形項の影響なのか、計算がうまくいっていないのか詳しい検証まではしていませんが、このような解析が短時間でできるのはさすがSciPyです。
まとめ
この記事はこれまでWATLABブログで取り扱った振動問題の過渡応答解析における総集編となりました。
1自由度の非減衰系から始め、減衰系→強制振動→サインスイープ加振→インパルス加振、N自由度問題への拡張→N自由度非線形…と進行することで、一通りの振動過渡応答解析のレシピが作れたと思います。自前でルンゲ・クッタを書いた経験があるとSciPyのodeintの高速性には感動します。
また記事内ではこれまでみていなかった全質点の挙動を可視化するコードを書いてみました。運動方程式の変化で挙動がどう変わるかを分析するのに動画は最適だと思います。是非参考にしてください。
このように全質点のデータを処理できるようになると、振動の実験で頻繁に使われている実稼働解析（Operating Deflection Shapes Analysis）や実稼働モーダル解析（Operating Modal Analysis）もしやすくなります。
今後そのようなコードも作ってみたいと思いました。
個人的な感想として、この記事の内容はブログ開始当初にできなくて諦めたので、今回何にも悩まず普通にできたことで成長を感じることができてよかったです。継続は力なりみたいですね。
学習のためのフルスクラッチは大きな意義があると思いますが、実際はSciPy等のライブラリで計算した方が良いと思いました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！