FFTは時系列データの周波数分析に重宝しますが、時間の変化はわかりません。スペクトログラムは周波数と時間変化の両方を分析可能な手法です。しかし計算方法は少々手順を踏みます。ここではPythonによるコーディングを1つずつ解説して行きます。
こんにちは。wat(@watlablog)です。
スペクトログラムは特に音声データ分析で絶大な効果を発揮する手法です。
ここではPythonによるスペクトログラムコードを自作したので紹介します！
ここでは周波数、時間、振幅の変化がひと目でわかるスペクトログラムを学びます。
しかし、Pythonの基本的なプログラミング手法を細かく説明しているわけではありません。もしPythonの基本文法等の学習をしたい場合はPython特化型学習サービスの「PyQ（パイキュー）」が大変オススメです！
スペクトログラムは時系列データから多彩な情報を得ることができる！
スペクトログラムとは？
スペクトログラムとは、音声をはじめとする様々な時系列データの分析に使われる可視化手法のことです。
このスペクトログラムは時間×周波数×振幅レベルという3つの要素で構成された3次元グラフです。
このページの後半ではPythonでスペクトログラムを計算するコードを載せますが、以下にそのプログラムで得られるグラフの例を先に紹介します。
スペクトログラム表示する前の入力データはこちら。
この波形はグランドピアノの「A（ラ）」の音を最低音から最高音までオクターブ毎に順番に打鍵していったものです。
wavファイルの音声をお聞きしたい方は、以下のメディアプレーヤーから再生してみて下さい。
※生のグランドピアノの音が再生されます。
そして以下が上の時系列データをスペクトログラム表示した結果です。
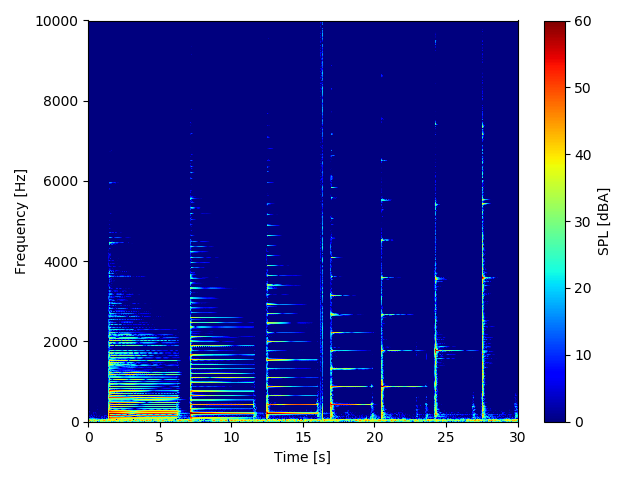
このように、スペクトログラム表示をすることで時系列データだけでは時間と振幅の関係しかわからなかったものに、周波数軸という奥行きを持たせることができます。
キレイだ！
この時系列データの処理に今回はSTFT（短時間フーリエ変換）という手法を用いました。
STFT(短時間フーリエ変換)とは？
STFT（Short-Time Fourier Transform : 短時間フーリエ変換）とは、時系列データを細かく窓（フレーム）で区切ってFFTし、その窓を順次横にずらしながらFFTを繰り返していく解析方法です。
以下は時系列データからフレームでデータを切り出し、順次FFTしていくSTFTからスペクトログラムまでの過程を示す図です。
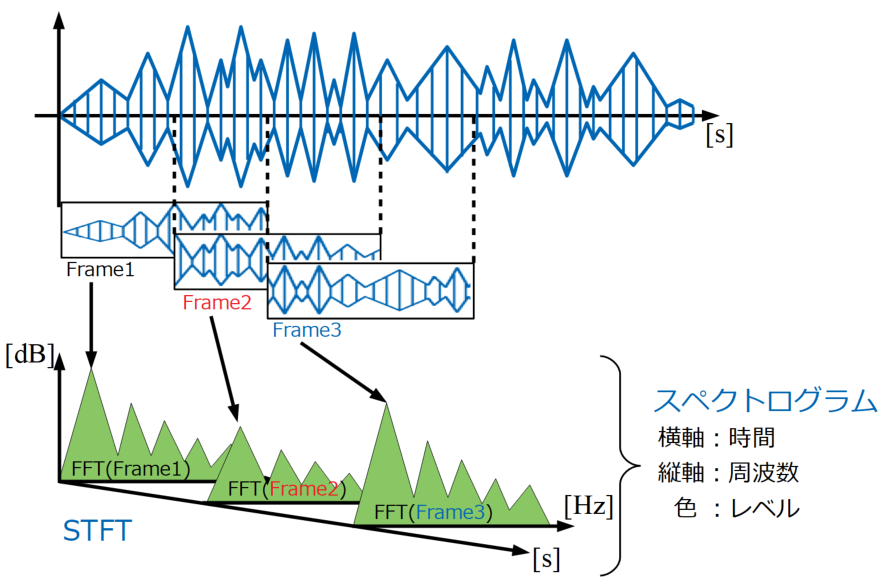
このように時系列データを抜き出す際にフレームをオーバーラップさせて計算するのが一般的です。
フレームで抜き出してきた短時間のフーリエ変換の結果は、時系列順に並べることで3次元の配列データになりますが、FFTの振幅レベルを色に変換することで横軸時間、縦軸周波数の2次元表示が可能になります。
スペクトログラムから得られる情報
スペクトログラムは世間で広く時系列データの分析に使われていますが、一般的にどんな情報を読み取っているのかを紹介します。
通常のFFTが周波数と振幅レベル（＋位相）という情報を持っているのに対し、スペクトログラムは時間の情報がプラスされています。
そのためスペクトログラムで主に分析する観点は「時間変化」になります。
以下は振幅レベルと周波数の時間変化の例です。
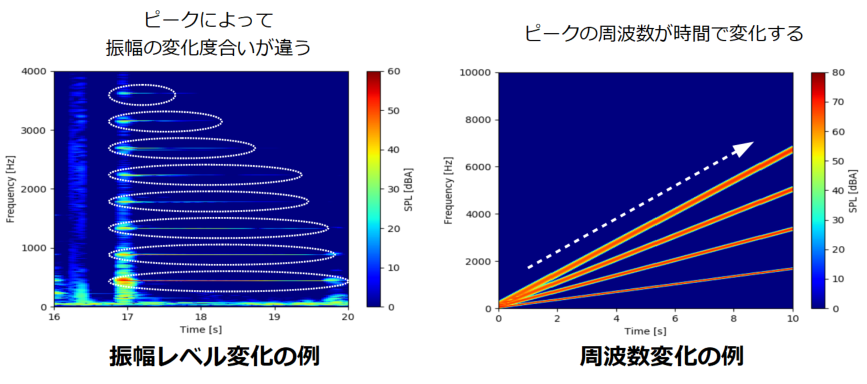
左の図は各ピーク（振幅レベルが卓越している部分）の振幅レベルが小さくなっていく（色が青くなっていく）時間がそれぞれ異なることを示しています。
右の図は時間が経つにつれピークが周波数方向に変化していくことを示しています。
このようにスペクトログラムではFFTで得られる情報に加えて、時間変化の情報を得ることができます。
Pythonでスペクトログラムを計算する方法
それではいよいよPythonによるSTFT計算とスペクトログラム表示までのプログラムを紹介します。
…とは言っても、実はWATLABブログでこれまで習得してきた内容の集大成となっていますので、それぞれ関連の記事を紹介していきます！
例により、ここに記載のプログラムは僕個人が学習して作った自作品です。間違いがある可能性もありますので使用には注意して下さい。
importするパッケージ
今回のSTFTとスペクトログラム表示のために、Pythonの外部ライブラリパッケージを宣言します。
インストールをしていない場合はpipで簡単にインストール可能なので、「Pythonのパッケージ管理ツール pipの使い方とコマンド集」の記事を確認して下さい。
|
1 2 3 4 |
import numpy as np from scipy import signal from scipy import fftpack import soundfile as sf |
配列処理のためのNumPyと科学技術計算のためのSciPy、wavファイルを使うためのPySoundFileを用意します。
時間波形データの用意(wavファイル読み込み)
まずは分析する時系列データを準備します。
具体的な方法は「PythonのPySoundFileでwavファイル波形表示」の記事で紹介した通りですが、コードを以下に示します。
|
1 2 3 |
def wavload(path): data, samplerate = sf.read(path) return data, samplerate |
オーバーラップ切り出し処理
時間波形を切り出す時にはオーバーラップ処理をできるようにしておきます。
オーバーラップ切り出し処理については「PythonでFFTをする前にオーバーラップ処理をしよう！」の記事に詳細を書いていますので参照下さい。
但し、上記記事とは戻り値に「最終時刻：final_time」を設定している部分に違いがあります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) /\ (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数（平均化に使うデータ個数） array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 final_time = (ps + Fs)/samplerate #切り出したデータの最終時刻 return array, N_ave, final_time # オーバーラップ抽出されたデータ配列とデータ個数、最終時間を戻り値にする |
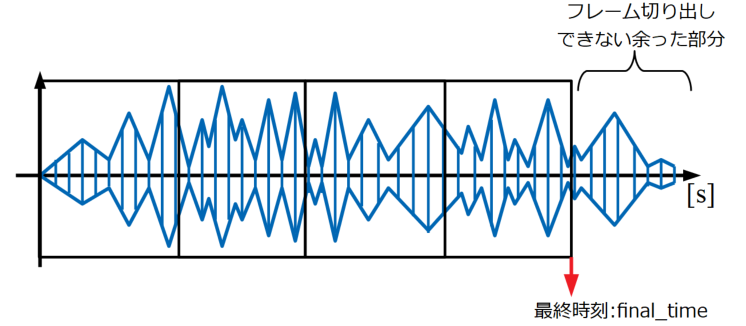
最終時刻とは、以下の図に示すように、フレームをオーバーラップして切り出してきた時の最終フレームの終端における時刻です。
この時刻はスペクトログラムの時間軸を作成する時に使います。
フレームサイズを決めてデータを切り出していくと、データ長とフレームサイズ、オーバーラップ率によってはフレーム切り出しできない余った部分がでます。
スペクトログラム表示の正確な時間軸を作るためには、この余った部分を除外する必要があるのでこのような計算をしています。
STFT計算
上記までで時間波形切り出しの関数は準備できたので、続いて周波数分析としてFFTを行うための関数を用意します。
窓関数と振幅補正係数
FFTをかけるために窓関数としてハニング窓の関数を用意します。詳細は「PythonでFFT！SciPyで窓関数をかける」をご確認下さい。
そして窓関数を使って振幅レベルを適正に評価するためには、振幅補正係数acf（Amplitude Correction Factor）が必要です。acfの詳しい内容は「窓関数使用時の補正！FFTの時に忘れがちな計算とは？」に書きました。
|
1 2 3 4 5 6 7 8 9 |
def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf |
デシベル(dB)変換
スペクトログラム表示をする場合は色成分をログスケールやdBスケールで表示させないと、音のような広い周波数帯域のデータを包括的に分析するには不向きになります（ピークの振幅レベルが10倍、100倍といった度合いで変化するのが普通なので）。
dBについての詳細は「Pythonで音圧のデシベル(dB)変換と逆変換式！」に記載しました。
|
1 2 3 |
def db(x, dBref): y = 20 * np.log10(x / dBref) # 変換式 return y # dB値を返す |
聴感補正（A特性補正）
聴感補正は音のデータを分析する時に通常使用します。人間の耳の特性に近づけた分析をすることで、実際の活用に役立てます。
聴感補正に関しては、「Pythonで聴感補正(A特性)の曲線を作る！」で式と実装を解説しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def aweightings(f): if f[0] == 0: f[0] = 1 else: pass ra = (np.power(12194, 2) * np.power(f, 4)) / \ ((np.power(f, 2) + np.power(20.6, 2)) * \ np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * \ (np.power(f, 2) + np.power(737.9, 2))) * \ (np.power(f, 2) + np.power(12194, 2))) a = 20 * np.log10(ra) + 2.00 return a |
FFT処理
FFTの関数は「PythonでFFT！SciPyのFFTまとめ」に記載した内容とほぼ同じですが、今回は聴感補正を考慮するので、最初からdB形式で計算するため、以下の順番で演算します。
①振幅補正係数acfをかける。
②dB変換する（聴感補正がdB値なので、dB同士のデータにする）。
③聴感補正曲線を足す。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
def fft_ave(data_array, samplerate, Fs, N_ave, acf): fft_array = [] fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 a_scale = aweightings(fft_axis) # 聴感補正曲線を計算 # FFTをして配列にdBで追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 for i in range(N_ave): fft_array.append(db\ (acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))\ , 2e-5)) fft_array = np.array(fft_array) + a_scale # 型をndarrayに変換しA特性をかける fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis |
ndarray形式であればforループを使わなくても配列演算ができるので、効率的ですね。
メイン実行文とグラフ表示
以上までのdef文で作成したコードを「function.py」というファイルで用意し、以下に示すメインコード（main_spectrogram.py）を実行することで冒頭に紹介したスペクトログラムを得ることができます（import文で関数をまとめたファイルを宣言する必要はあります）。
関数の使い方は「Pythonの関数 def文の使い方！引数や別ファイル式も解説」で説明しています。
wavファイルが無くても、自分で波形を作成（samplerate, x, dataを決めるだけ）して使っても動作しますので、是非お試し下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import function import numpy as np from matplotlib import pyplot as plt path = 'ff_A.wav' #ファイルパスを指定 data, samplerate = function.wavload(path) #wavファイルを読み込む x = np.arange(0, len(data)) / samplerate #波形生成のための時間軸の作成 # Fsとoverlapでスペクトログラムの分解能を調整する。 Fs = 4096 # フレームサイズ overlap = 90 # オーバーラップ率 # オーバーラップ抽出された時間波形配列 time_array, N_ave, final_time = function.ov(data, samplerate, Fs, overlap) # ハニング窓関数をかける time_array, acf = function.hanning(time_array, Fs, N_ave) # FFTをかける fft_array, fft_mean, fft_axis = function.fft_ave(time_array, samplerate, Fs, N_ave, acf) # スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置 fft_array = fft_array.T # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure() ax1 = fig.add_subplot(111) # データをプロットする。 im = ax1.imshow(fft_array, \ vmin = 0, vmax = 60, extent = [0, final_time, 0, samplerate], \ aspect = 'auto',\ cmap = 'jet') # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('SPL [dBA]') # 軸設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Frequency [Hz]') # スケールの設定をする。 ax1.set_xticks(np.arange(0, 50, 5)) ax1.set_yticks(np.arange(0, 20000, 2000)) ax1.set_xlim(0, 30) ax1.set_ylim(0, 10000) # グラフを表示する。 plt.show() plt.close() |
追記：wavファイルが無いけどすぐ試したい方は自分で時間波形を作ろう！
メインのコードを変更
スペクトログラムはwavファイルでなくても描くことができます。上記のコードはモノラルのwavファイルを使うことが前提の内容でしたが、wavファイルって一回録音して、ファイル移動して…ってひと手間が面倒ですよね。
手っ取り早くお手元の環境でSTFT解析を行い、スペクトログラム表示を試したい方のために、以下にwavファイルが無くても動作するメインの.pyファイルを示します。
コードの冒頭でscipyをimportし、chirp信号という時間で周波数が変化する信号を生成しています。
チャープ信号については「Pythonでチャープ信号！周波数スイープ正弦波の作り方」に詳しく書いてありますので、是非併せてご覧下さい！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import function import numpy as np from matplotlib import pyplot as plt from scipy.signal import chirp # チャープ信号を作成 t = np.linspace(0, 5, 128000) data = chirp(t, f0=1, f1=2000, t1=5, method='linear') samplerate = 25600 x = np.arange(0, len(data)) / samplerate #波形生成のための時間軸の作成 # Fsとoverlapでスペクトログラムの分解能を調整する。 Fs = 4096 # フレームサイズ overlap = 75 # オーバーラップ率 # オーバーラップ抽出された時間波形配列 time_array, N_ave, final_time = function.ov(data, samplerate, Fs, overlap) # ハニング窓関数をかける time_array, acf = function.hanning(time_array, Fs, N_ave) # FFTをかける fft_array, fft_mean, fft_axis = function.fft_ave(time_array, samplerate, Fs, N_ave, acf) # スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置 fft_array = fft_array.T # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure() ax1 = fig.add_subplot(111) # データをプロットする。 im = ax1.imshow(fft_array, \ vmin = -10, vmax = 60, extent = [0, final_time, 0, samplerate], \ aspect = 'auto',\ cmap = 'jet') # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('SPL [dBA]') # 軸設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Frequency [Hz]') # スケールの設定をする。 ax1.set_xticks(np.arange(0, 120, 1)) ax1.set_yticks(np.arange(0, 20000, 500)) ax1.set_xlim(0, 5) ax1.set_ylim(0, 2000) # グラフを表示する。 plt.show() plt.close() |
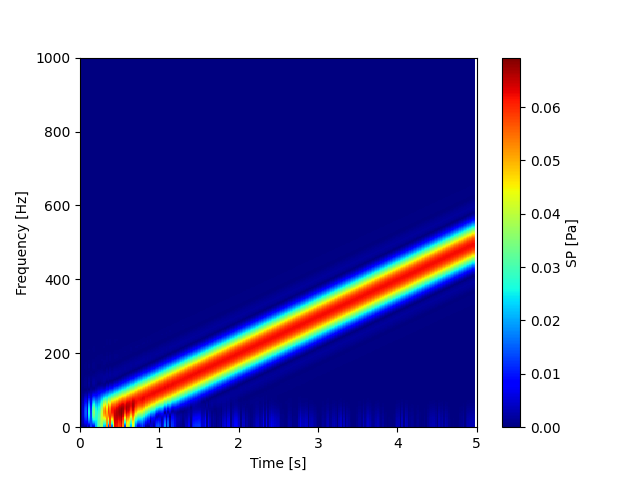
実行すると、以下のグラフが表示されると思います。5[s]間で0[Hz]から2000[Hz]まで周波数が増加している様子がはっきりと確認できますね！
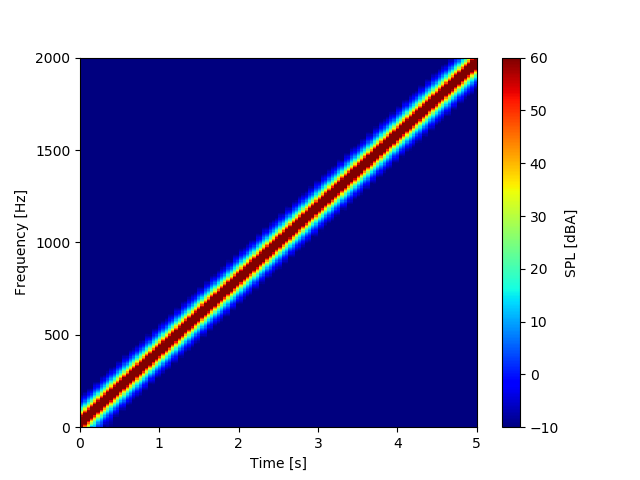
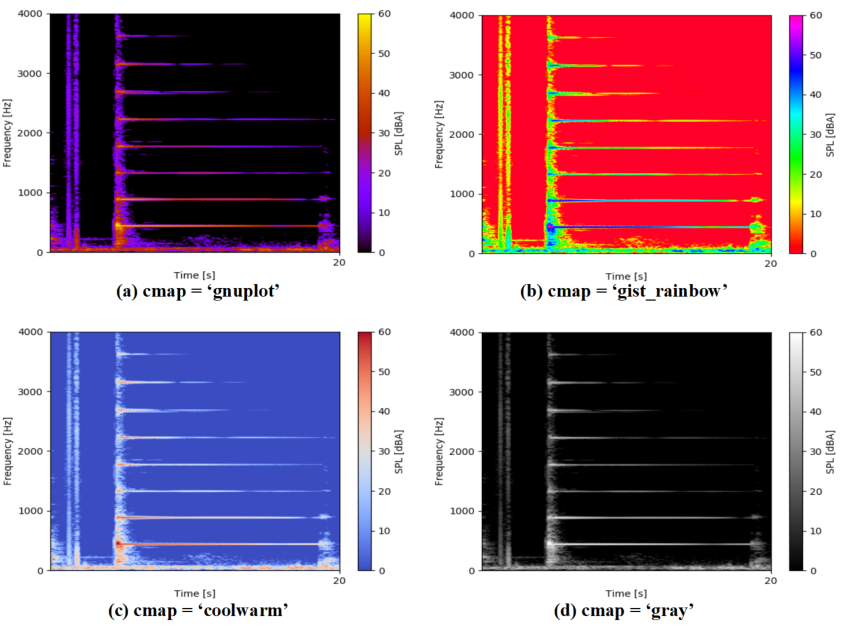
補足：カラーマップの種類について
スペクトログラムは色を使ってデータを表現します。
この色のパターンは非常に多くの種類があり、imshow関数内で引数としているcmapの指定で変更することが可能です。
以下の図はcmap違いのスペクトログラムです。「参考外部サイト様：color exsample code」に良いリストがありますので、お好みの設定を見つけて下さい。
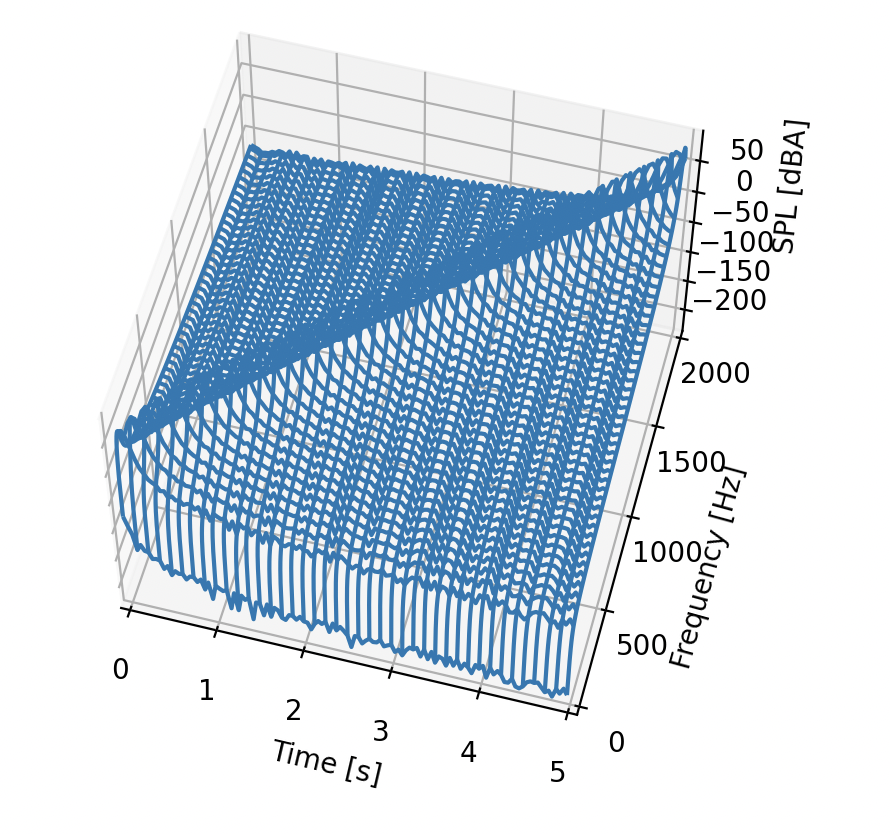
おまけ：3Dグラフで表示する方法
こちらはおまけです。スペクトログラムといえばカラーマップを使って描画するのが一般的ですが、3Dグラフの方が見やすい場合もあるかも知れません。以下のコードはnp.meshgrid()でデータを整形してplot_wireframe()で3Dのワイヤーフレームプロットをするコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
import function import numpy as np from matplotlib import pyplot as plt from scipy.signal import chirp # チャープ信号を作成 t = np.linspace(0, 5, 128000) data = chirp(t, f0=1, f1=2000, t1=5, method='linear') samplerate = 25600 x = np.arange(0, len(data)) / samplerate #波形生成のための時間軸の作成 # Fsとoverlapでスペクトログラムの分解能を調整する。 Fs = 4096 # フレームサイズ overlap = 75 # オーバーラップ率 # オーバーラップ抽出された時間波形配列 time_array, N_ave, final_time = function.ov(data, samplerate, Fs, overlap) # ハニング窓関数をかける time_array, acf = function.hanning(time_array, Fs, N_ave) # FFTをかける fft_array, fft_mean, fft_axis = function.fft_ave(time_array, samplerate, Fs, N_ave, acf) # スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置 fft_array = fft_array.T # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure() ax1 = fig.add_subplot(111, projection='3d') # 軸設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Frequency [Hz]') ax1.set_zlabel('SPL [dBA]') # スケールの設定をする。 ax1.set_xticks(np.arange(0, 120, 1)) ax1.set_yticks(np.arange(0, 20000, 500)) time_max = 5 ax1.set_xlim(0, time_max) freq_max = 2000 ax1.set_ylim(0, freq_max) # meshgrid用にデータをつくる（3Dのwireframeは範囲外のデータも可視化されるので、不要なデータを削除する） time_axis = np.linspace(0, final_time, len(fft_array[0])) time_axis = time_axis[0:int(time_max / time_axis[1])] fft_axis = fft_axis[0:int(freq_max / fft_axis[1])] fft_array = np.delete(fft_array, np.s_[int(time_max / time_axis[1]):len(fft_array):], axis=1) fft_array = np.delete(fft_array, np.s_[int(freq_max / fft_axis[1]):len(fft_array):], axis=0) X, Y = np.meshgrid(time_axis, fft_axis) Z = fft_array.reshape(len(X), -1) ax1.plot_wireframe(X, Y, Z) # グラフを表示する。 plt.show() plt.close() |
結果はこちら。実行結果はマウスでぐるぐる回すことが可能です（下のは画像ですが）。
matplotlibによる3Dプロットについては、以下の記事も参考にしてください。
・Python/matplotlib3Dプロット!面と散布図を作成
おまけ：dB表示やA補正をしないシンプルなスペクトログラム作成コード
これまでのSTFT、及びスペクトログラム表示のコードはdB変換やA補正を標準で行なっていました。振動現象や音響現象は周波数によって振幅レベルの差が大きいので、通常は対数表示やdB変換をするのですが、それらを使わないシンプルな分析も需要があるようです。
以下のコードはfft_ave関数の引数に「no_db_a」を追加し、no_db_a=Trueの時はdB変換やA補正をしないようにする修正を行なったものです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 |
import numpy as np from scipy import signal from scipy import fftpack from matplotlib import pyplot as plt # オーバーラップをかける関数 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数（平均化に使うデータ個数） array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 final_time = (ps + Fs)/samplerate # 切り出したデータの最終時刻 return array, N_ave, final_time # オーバーラップ抽出されたデータ配列とデータ個数、最終時間を戻り値にする # ハニング窓をかける関数（振幅補正係数計算付き） def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf # dB(デシベル）演算する関数 def db(x, dBref): y = 20 * np.log10(x / dBref) # 変換式 return y # dB値を返す # 聴感補正(A補正)する関数 def aweightings(f): if f[0] == 0: f[0] = 1 ra = (np.power(12194, 2) * np.power(f, 4))/\ ((np.power(f, 2) + np.power(20.6, 2)) * np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * (np.power(f, 2) + np.power(737.9, 2))) * (np.power(f, 2) + np.power(12194, 2))) a = 20 * np.log10(ra) + 2.00 return a # 平均化FFTする関数 def fft_ave(data_array, samplerate, Fs, N_ave, acf, no_db_a): fft_array = [] fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 a_scale = aweightings(fft_axis) # 聴感補正曲線を計算 # FFTをして配列にdBで追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 for i in range(N_ave): # dB表示しない場合とする場合で分ける if no_db_a == True: fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))) else: fft_array.append(db (acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2)) , 2e-5)) # 型をndarrayに変換しA特性をかける(A特性はdB表示しない場合はかけない） if no_db_a == True: fft_array = np.array(fft_array) else: fft_array = np.array(fft_array) + a_scale fft_mean = np.mean(np.sqrt(fft_array ** 2), axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis # Fsとoverlapでスペクトログラムの分解能を調整する。 Fs = 4096 # フレームサイズ overlap = 90 # オーバーラップ率 # 波形を作る samplerate = 44100 t_max = 5 x = np.arange(0, t_max, 1/samplerate) data = signal.chirp(x, f0=1, f1=500, t1=5, method='linear') # オーバーラップ抽出された時間波形配列 time_array, N_ave, final_time = ov(data, samplerate, Fs, overlap) # ハニング窓関数をかける time_array, acf = hanning(time_array, Fs, N_ave) # FFTをかける fft_array, fft_mean, fft_axis = fft_ave(time_array, samplerate, Fs, N_ave, acf, no_db_a=True) # スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置 fft_array = fft_array.T # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure() ax1 = fig.add_subplot(111) # データをプロットする。 im = ax1.imshow(fft_array, vmin=0, vmax=np.max(fft_array), extent=[0, final_time, 0, samplerate], aspect='auto', cmap='jet') # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('SP [Pa]') # 軸設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Frequency [Hz]') # スケールの設定をする。 ax1.set_xticks(np.arange(0, 50, 1)) ax1.set_yticks(np.arange(0, 20000, 200)) ax1.set_xlim(0, 5) ax1.set_ylim(0, 1000) # グラフを表示する。 plt.show() plt.close() |
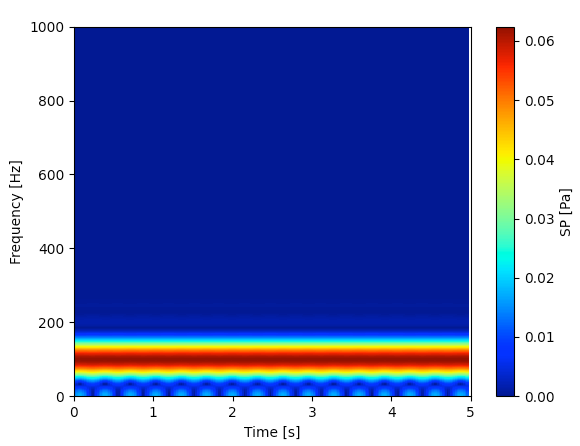
例えば、振幅1で生成した波形は以下のように色レベルでも1を確認する事ができます。「A補正なしのリニア表示」とでも呼ぶのかな？
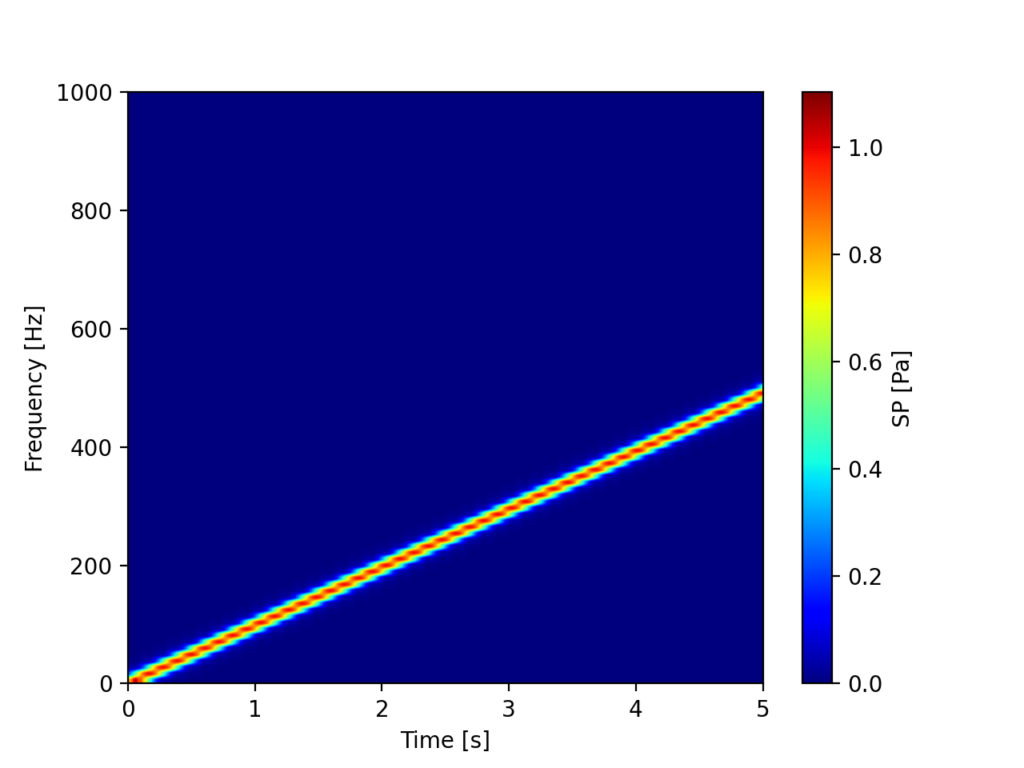
おまけ：録音してスペクトログラムを作るコード
録音したデータに対してスペクトログラムを作る需要も結構あるようです。
以下のコードはPyAudioを使って録音したデータに対してSTFT計算を行い、スペクトログラム表示するコードです。
録音については「PythonのPyAudioで音声録音をする簡単な方法」に詳細を記載していますので、是非ご覧下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 |
import numpy as np from scipy import signal from scipy import fftpack from matplotlib import pyplot as plt import pyaudio def record(index, samplerate, fs, time): pa = pyaudio.PyAudio() data = [] dt = 1 / samplerate # ストリームの開始 stream = pa.open(format=pyaudio.paInt16, channels=1, rate=samplerate, input=True, input_device_index=index, frames_per_buffer=fs) # フレームサイズ毎に音声を録音していくループ for i in range(int(((time / dt) / fs))): frame = stream.read(fs) data.append(frame) # ストリームの終了 stream.stop_stream() stream.close() pa.terminate() # データをまとめる処理 data = b"".join(data) # データをNumpy配列に変換 data = np.frombuffer(data, dtype="int16") / float((np.power(2, 16) / 2) - 1) return data, i # オーバーラップをかける関数 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数（平均化に使うデータ個数） array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 final_time = (ps + Fs)/samplerate # 切り出したデータの最終時刻 return array, N_ave, final_time # オーバーラップ抽出されたデータ配列とデータ個数、最終時間を戻り値にする # ハニング窓をかける関数（振幅補正係数計算付き） def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf # dB(デシベル）演算する関数 def db(x, dBref): y = 20 * np.log10(x / dBref) # 変換式 return y # dB値を返す # 聴感補正(A補正)する関数 def aweightings(f): if f[0] == 0: f[0] = 1 ra = (np.power(12194, 2) * np.power(f, 4))/\ ((np.power(f, 2) + np.power(20.6, 2)) * np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * (np.power(f, 2) + np.power(737.9, 2))) * (np.power(f, 2) + np.power(12194, 2))) a = 20 * np.log10(ra) + 2.00 return a # 平均化FFTする関数 def fft_ave(data_array, samplerate, Fs, N_ave, acf, no_db_a): fft_array = [] fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 a_scale = aweightings(fft_axis) # 聴感補正曲線を計算 # FFTをして配列にdBで追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 for i in range(N_ave): # dB表示しない場合とする場合で分ける if no_db_a == True: fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))) else: fft_array.append(db (acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2)) , 2e-5)) # 型をndarrayに変換しA特性をかける(A特性はdB表示しない場合はかけない） if no_db_a == True: fft_array = np.array(fft_array) else: fft_array = np.array(fft_array) + a_scale fft_mean = np.mean(np.sqrt(fft_array ** 2), axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis # Fsとoverlapでスペクトログラムの分解能を調整する。 Fs = 4096 # フレームサイズ overlap = 90 # オーバーラップ率 # 録音して波形を作る（indexはPCによる） index = 0 samplerate = 44100 t_max = 5 data, i = record(index, samplerate, Fs, t_max) x = np.arange(0, Fs * (i+1) * (1 / samplerate), 1 / samplerate) # オーバーラップ抽出された時間波形配列 time_array, N_ave, final_time = ov(data, samplerate, Fs, overlap) # ハニング窓関数をかける time_array, acf = hanning(time_array, Fs, N_ave) # FFTをかける fft_array, fft_mean, fft_axis = fft_ave(time_array, samplerate, Fs, N_ave, acf, no_db_a=True) # スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置 fft_array = fft_array.T # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure() ax1 = fig.add_subplot(111) # データをプロットする。 im = ax1.imshow(fft_array, vmin=0, vmax=np.max(fft_array), extent=[0, final_time, 0, samplerate], aspect='auto', cmap='jet') # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('SP [Pa]') # 軸設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Frequency [Hz]') # スケールの設定をする。 ax1.set_xticks(np.arange(0, 50, 1)) ax1.set_yticks(np.arange(0, 20000, 500)) ax1.set_xlim(0, 5) ax1.set_ylim(0, 2000) # グラフを表示する。 plt.show() plt.close() |
下図は口笛を吹いてみた結果です。
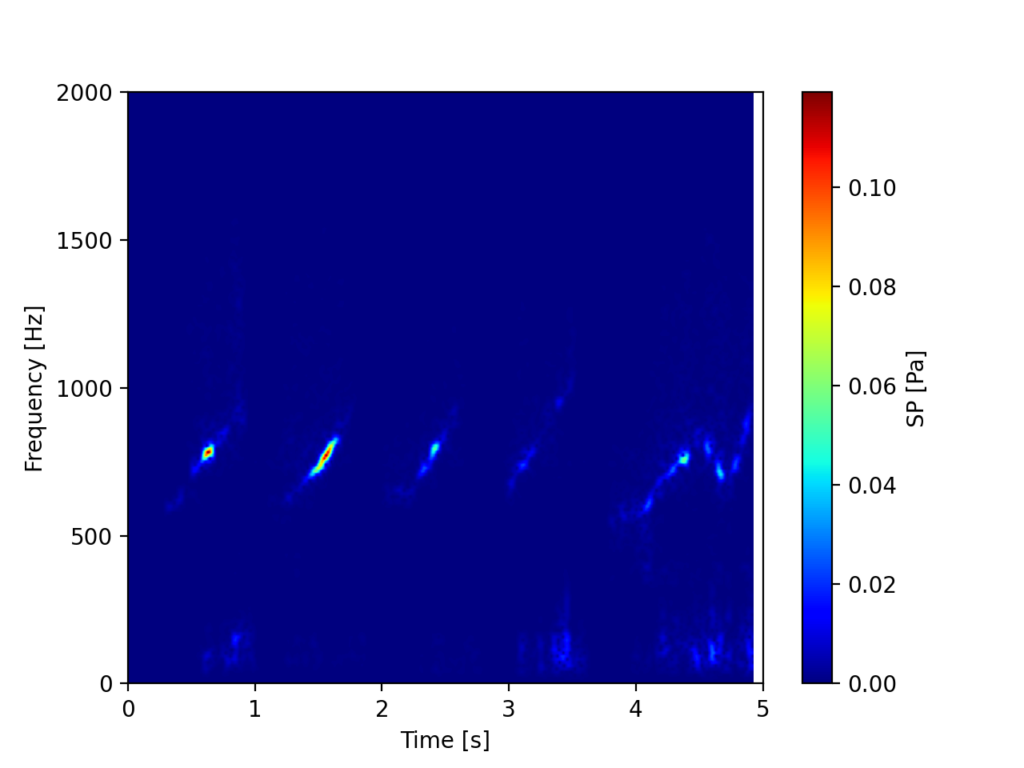
Scipyのsignal.spectrogram()を使ってみた
流石Python。外部ライブラリであるScipyにもスペクトログラムを計算するメソッドがあるようです。
使い方はまずは公式ドキュメントをご覧下さい。
公式ドキュメント：scipy.signal.spectrogram
コードがかなり短くなる(全コード)
scipy.signal.spectrogramを使うとスペクトログラムをたったこれだけのコードで書く事が出来ます。上で自作したコードと比べると雲泥の差ですね。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import numpy as np import scipy.signal as signal import matplotlib.pylab as plt # サンプル波形を生成 fs=44100 # サンプリングレート[Hz] time = 5 # 波形長[s] x = np.arange(0, time, 1/fs) data = signal.chirp(x, f0=1, f1=500, t1=5, method='linear') # スペクトログラムを計算（f:周波数軸, t:セグメント時間, Sxx:スペクトログラム） f, t, Sxx = signal.spectrogram(data, fs, nfft=44100, nperseg=1024, mode='magnitude', window='hann') # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure() ax1 = fig.add_subplot(111) # データをプロットする。 im = ax1.pcolormesh(t, f, Sxx, cmap="jet") cbar = fig.colorbar(im) cbar.set_label('SP [Pa]') # 軸設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Frequency [Hz]') # スケールの設定をする。 ax1.set_xticks(np.arange(0, 50, 1)) ax1.set_yticks(np.arange(0, 20000, 200)) ax1.set_xlim(0, 5) ax1.set_ylim(0, 1000) # グラフを表示する。 plt.show() plt.close() |
以下が結果。ここではnfftとnpersegで分解能の調整をしています。
振幅成分がおかしい
先ほどのスペクトログラムはmode='magnitude'で計算しており、振幅成分を出しているようなのですが、理想波形の振幅が1なのに対してスペクトログラムの振幅が0.06とかなり小さくなっていました（先に紹介した自作スペクトログラムコードではちゃんと1になっていたのに）。
フーリエ変換は一定フレーム内で計算するため、時間変動の影響で振幅が1にならない可能性もあります。しかし、以下のように100[Hz]一定振幅にしてみても傾向は変わらず。
「窓関数使用時の補正！FFTの時に忘れがちな計算とは？」でやったように、窓関数にhannを指定し、Amplitude Correlation Factorを導入したり、「PythonでFFT実装!SciPyのフーリエ変換まとめ」で検証したように（N/2）で割ってみたり、あえてmode='complex'にして、ReとImから振幅成分を計算したり（これはmode='magnitude'と同じになりましたが）…と色々やってみましたが、全て失敗。
まだまだsignal.spectrogramの仕様が理解できていないようです…。
ライブラリを思い通り使えると便利なのですが、謎が残りました。
僕はしばらく自作コードを使っていきます。
もしsignal.spectrogramで正しい振幅成分を計算する方法をご存知の方はこの記事の下か、Twitter(@watlablog)までご連絡頂けると助かります！
まとめ
少し長くなってしまいましたが、本記事では音声データのスペクトログラムを計算する一連の方法を書きました。
しかし新しいことはほとんど無く、これまでWATLABブログで扱ってきた内容（wavファイルの取り扱い、波形切り出し、窓関数の取り扱い、dB変換、聴感補正、多段のFFT）が多くありました。
カラーマップを変更することでスペクトログラムの見え方を大きく変えることができました。
今回は音声データの強力な分析手法であるSTFTやスペクトログラム表示を習得しました！これで色々なデータから様々な情報を得ることができるようになるね！
X（旧Twitter）でも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
質問させてください！
「PythonでFFTをする前にオーバーラップ処理をしよう！」でも記述してあったのですが、
FFTをした後に平均化処理をする理由がよく理解できません。お教えしていただけたら幸い
です。よろしくお願いします。
watです。記事を読んで頂きありがとうございます。
平均化ですが、ここに書いてある内容は主に実験データを想定しています。
理想波形であれば1フレームのFFTも複数フレームを平均化したFFTも変わりません。
しかし、実験データは時間によって主要次数の振幅が安定していないことも多々あります。
平均化処理は、不安定なデータを綺麗にするために行います。
おそらく大抵の商用FFTアナライザー（100万円くらいするやつ）にはこのような機能が付いていると思います。
回答が的を射てなかったらすみません…。その場合はまた質問して下さい！
なるほど！！
理解することができました！ありがとうございます！
ご連絡ありがとうございます！
また何かわからないことがありましたらコメントよろしくお願いします！
突然失礼します。ここにあるコードでfftを行ったのですが、 data_array[i]= data_array[i] * han # 窓関数をかける
ValueError: operands could not be broadcast together with shapes (4096,2) (4096,) というエラーが出て困っています。このエラーの解決方法について助言をいただけたら幸いです。
コメントありがとうございます。
過去に似たような質問を頂いたことがあるのですが、ステレオ録音して作成したwavファイルをご使用していますでしょうか？
ここに記載のコードはモノラルのwavにのみ対応していますので、まずはそこをご確認下さい。
dataを定義した直後に、print(data.ndim)とすることでdataの次元を調査することも可能です。その次元が2とかですとステレオのwavである可能性が高いです。
また、もしwavファイルが原因で発生しているエラーでしたら、記事内の「追記：wavファイルが無いけどすぐ試したい方は自分で時間波形を作ろう！」の項目に記載してあるコードをお試し下さい。
このコードはwavファイルを使わないでSTFT計算をするバージョンです。
もしこのコードがエラーなく実行できれば、他は問題ないということになります。
もし僕のこの回答が検討はずれである場合は再度コメント頂ければと思います！よろしくお願いします！
本当にありがとうございます！
ご指摘の通り、ステレオ録音で作成したwavファイルだったので、
data, samplerate = function.wavload(path) #wavファイルを読み込む
と
x = np.arange(0, len(data)) / samplerate #波形生成のための時間軸の作成
の間に
♯ステレオ2chの場合、LchとRchに分割
data_l = data[:, 0]
data_r = data[:, 1]
♯ 入力をモノラル化
data = (0.5 * data_l) + (0.5 * data_r)
を入れて、ファイルをモノラルに変えたら無事動きました。
ご連絡ありがとうございます。
解決したようでよかったです！また何かご不明点ありましたらコメント下さい！
質問失礼します。
スペクトログラムに表示されているSPLのデータの値はどこに格納されているのでしょうか？
データを一覧でみたいのですが。。。
fft_array？
ご訪問ありがとうございます。
スペクトログラムで表示されているデータはご推察の通り、fft_arrayに入っています。
def fft_ave()の結果のfft_arrayをfft_array.Tと転置させてax1.imshow(fft_array,…)とmatplotlibでプロットしています。
ご回答ありがとうございます！
実際にfft_arrayをprintすると以下のようなります。
[[-139.39209144 -127.47142483 -122.92904072 … -117.88843985
-121.33788775 -125.57795728]
[ -35.09114161 -35.37201986 -36.05485323 … -41.30974036
-37.42815004 -37.43793617]
[ -17.06772899 -17.50646536 -18.35489237 … -15.32351833
-15.61655708 -15.99538017]
…
[ 1.85881599 -2.20633606 -10.41866818 … 9.30049942
3.95455108 -3.43244636]
[ 6.967212 6.52847562 5.68004861 … 8.71142265
8.41838391 8.03956081]
[ 8.08926983 7.80839159 7.12555822 … 1.87067109
5.75226141 5.74247527]]
これはどのように読めばいいのでしょうか？
[]は右にしたがってX軸方向、二つ目の[]は上にy軸方向など。値の間隔はあるのかどうか。
また、カラーバーは０〜６０dbまでなのになぜマイナスの値が表示されるのでしょうか？（スペクトログラム上でマウスをドラッグした場合にもマイナスの値が見受けられました。）
至らぬ点が多いですが、よろしくお願いいたします。
スペクトログラムは2次元のデータなので確かにわかりにくいですよね。
fft_array.Tと転置する前のfft_arrayの方で説明すると、これはFFTをかけていった結果をどんどん蓄積させているデータという意味を持ちます。
>>これはどのように読めばいいのでしょうか？
そのため、fft_array[i]と1行だけ抽出すると、それはスペクトグラムを縦方向（任意時間）でスライスした時のFFT波形を示します。
[[0番目のFFT波形],[1番目のFFT波形],…,[i番目のFFT波形]]です。
FFT波形はデータが周波数順になっています。
fft_arrayには周波数軸や時間軸の情報が無いので、fft_axisysamplerateから自分で計算する必要があります。
>>カラーバーは０〜６０dbまでなのになぜマイナスの値が表示されるのでしょうか？
これは実際にマイナスの値があるという意味で間違いありません。
カラーバーは見やすいように手動で調整しているだけです。指定しなければオートレンジになると思います。
以上、よろしくお願い致します。
ご回答ありがとうございます！
おかげさまで理解することができました。ありがとうございます！
ご連絡ありがとうございます。
理解して頂けてよかったです。
今後ともよろしくお願いします！
質問失礼します！
オーバーラップする意味とかは分かったのですが、スペクトログラムで表示する際はオーバーラップによって重複したフレーム部分はどう処理しているのかが分かりません。
教えて下さると助かります。
ご訪問ありがとうございます。
オーバーラップ率を大きくすると、平均化して1枚の周波数波形を出す時には平均化する枚数が増えます。
スペクトログラムを計算する時は、オーバーラップによって得られた各周波数波形は平均化せず、単純に時間軸方向に並べられます。
まずここが、通常の平均化FFTとスペクトログラムの違いです。
そのため、スペクトログラムでオーバーラップによって重複した部分は単純に周波数波形が増える事になり、これは時間分解能が上がる事を意味します。
オーバーラップ率0％でスペクトログラムを計算して時間分解能（dt)が0.1[s]である場合、
オーバーラップ率50%でスペクトログラムを算出するとdt=0.05[s]と半分になります。
（時間に対する変化を捉えやすくなります）
是非実際に数値を変更してスペクトログラムを眺めてみて下さい。
よろしくお願い致します。
時間分解能を上げる方法としてが最もな理由ですが、もう一つ理由が（確か）合って、窓関数をかけたことでのデータ圧縮を補完するためにオーバーラップで窓関数のゲインが高いところがなるべくくっつくようにするためでもあります。
小野測器でハニング窓を使用している場合のオーバーラップ率を66.7%(2/3)以上と推奨しているのは、ハニング窓のスペクトル振幅の窓関数補正値が2/3であるからだったと思います。
検索してもこの記述が無く、断言出来ないところが辛いところですが、ハニング窓を66.7%で書いていけば、私の言っていることが何となく伝わるかなと思います。
ゼローク様、こちらにもコメントありがとうございます。
オーバーラップの記事で絵を描いておきながらこちらではその説明を省いてしまいました。
ただハニング窓の補正値と紐つけた説明は非常にわかりやすかったです。
実務では伝統のようにそのルールに則っていましたが、今頭の中がクリアになったと思います。
ありがとうございました。
質問失礼いたします。
上記のメイン実行文の通りにpythonに入力したのですが、スペクトログラムの画像が表示されません…。表示されないというか、グラフは出てくるけど色がついてないという状態です。エラーの箇所を見てみると、「NameError: name ‘fft_array’ is not defined」と出たり、「NameError: name ‘im’ is not defined」と表示されています。この場合は何処を直したらよいでしょうか？初心者的な質問ですみません…。
ご訪問ありがとうございます。
コピペしたコードの中に「fft_array = 〜」というコードは入っていますか？
「〜is not defined」というエラーは変数を定義する前に使用した時に出ますので、文字が間違っているか、コピペ忘れ等が考えられます。
エラーの発生している行より上をみて、変なスペースや文字間違えが無いかを確認してみて下さい。
もし解決しない場合はより詳しい情報（Python環境（PyCharm使用、Python3.7で実行…エラー行は○○、fft_array=の付近のコードをここにコピペ…）等）を記載して頂ければ、何かしら力になれると思います！
よろしくお願いします。
返信ありがとうございます。
python3.9.1で実行しております。
エラーが起こっている箇所は、行数は分からないのですが、
# データをプロットする。
>>> im = ax1.imshow(fft_array, \
… vmin = 0, vmax = 60,
… extent = [0, final_time, 0, samplerate], \
… aspect = ‘auto’,\
… cmap = ‘jet’)
Traceback (most recent call last):
File “”, line 1, in
NameError: name ‘fft_array’ is not defined
>>> # FFTをかける
>>> fft_array, fft_mean, fft_axis = function.fft_ave(time_array, samplerate, Fs, N_ave, acf)
Traceback (most recent call last):
File “”, line 1, in
AttributeError: module ‘function’ has no attribute ‘fft_ave’
>>>
>>> # スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置
>>> fft_array = fft_array.T
Traceback (most recent call last):
File “”, line 1, in
NameError: name ‘fft_array’ is not defined
という箇所です。
うーん、なんでしょう？これは初めてのお問い合わせですね。
Pythonのバージョンは僕は3.7.7を使っています。
物によっては新しいPythonバージョンにライブラリが対応していないという事はよくあるそうですが…今は不明です。
確認ですが、
①function.pyとmain.pyと二つのファイルを同じフォルダ作っている。
②function.pyには以下の関数が順番に書いてある。
def wavload(path):
def ov(data, samplerate, Fs, overlap):
def hanning(data_array, Fs, N_ave):
def db(x, dBref):
def aweightings(f):
def fft_ave(data_array, samplerate, Fs, N_ave, acf):
という所は大丈夫でしょうか？
エラーの発生している場所がわからない場合はprint文を1行ずつ挟んで実行して確認するという手もあります。
できればバージョンを揃えるのが良いと思いますが、まずは上記方法等でデバッグをしてみて下さい。
音声ファイルを入れたフォルダを読み込ませて一気にスペクトログラム表示するにはどうすればよいか教えて頂きたいです。
ご訪問ありがとうございます。
ちょうどその目的に合致しそうな記事があります。
「Pythonでフォルダ内全wavをスペクトログラムに変換してみた」
という記事をご確認ください。
よろしくお願いします。
質問失礼します。
最近、Pythonの勉強を始めたものです。wat様のブログには大変お世話になっております。
質問なのですが、「wavファイルが無いけどすぐ試したい方は自分で時間波形を作ろう！」の所で、ModuleNotFoundError: No module named ‘function’が出てしまいまうのですが、なぜでしょうか。初心者的な質問ですみません。
Pythonのバージョンは3.8.3です。
解決しました！
とても勉強になりました。ありがとうございます。
ご訪問ありがとうございます。
また、自己解決されたようでよかったです。
またよろしくお願いします！
質問失礼致します。
fft_arrayを用いて”何秒に何Hz”の音が鳴っているか数値で得ることは可能でしょうか？
fft_array.Tをcsvファイルに書き込み、”何dBが何秒”に鳴ったかを出すことはできたのですが、何Hzかがどうしてもわからず教えて頂きたいです。
よろしくお願い致します。
ご訪問ありがとうございます。
fft_arrayは3次元のデータであり、dB値と時間、周波数の情報を持ちます。
そのため、csvから任意時間におけるdB値を取得できている段階であれば周波数成分を求める事が可能です。
時間を読んだ軸とは異なる軸が周波数を意味していますので、
0番目、1番目…i番目と並んでいるiに周波数分解能（1/フーリエ変換時のフレーム周期）を乗じた値が周波数です。
まずはこの考え方でデータを再度ご確認頂ければと思います。
以下の記事はスペクトログラムからピーク値を抽出するコードを紹介しています。
もしかしたら参考になるかもしれません。
https://watlab-blog.com/2020/09/29/findpeaks-spectrogram/
以上、よろしくお願い致します。
ご回答ありがとうございます！！
質問失礼します。
分かりやすい説明で、初心者の私でも無事スペクトログラム表示できました。
さて、周波数軸(縦軸)を対数表示でグラフ作成したいのですが、なかなかうまくいきません。どのようなコードを書けばよいか教えて頂けませんでしょうか。よろしくお願いいたします。
ご訪問ありがとうございます。
対数表示はmatplotlibの.set_yscaleで行います。
但し0から始まるスケールはバグってしまうので、以下のように記述すると良いと思います。
ax1.set_ylim(0.01, 10000)
ax1.set_yscale(‘log’)
以上、ご確認よろしくお願い致します。
ありがとうございます。
無事できました！
ご報告ありがとうございます。
よかったです。
いつも参考にさせて頂いております。
0.1秒未満の短い音のスペクトログラムを得たいのですが、上記のコードで実行したところ、直線が数本描写されるだけで正しいスペクトログラムが得られません。(グラフのスケールは変えました)
要領を得ない質問ではありますがアドバイス等頂けないでしょうか。
ご訪問ありがとうございます。
時間分解能によりますが、短い音の場合はそのような結果になり得ます。
フーリエ変換はフレームと呼ばれる範囲で時間を切り取って計算するため、データによってフレームサイズやオーバーラップを調整した方が良いでしょう。
例えば、フレームサイズを小さくしてオーバーラップ率を上げると時間分解能が上がり、縦線の数が増えると思います。
その場合は逆に周波数分解能が下がり横線の数が減るので、ちょうど良い条件はデータ毎に探す必要があります。
お返事遅れて申し訳ありません。
ありがとうございます。そのように調整する場合今回のコードのどのような箇所を変更しながら調節したら良いのでしょうか。
お恥ずかしながらプログラミング初心者なので教えていただきたいです。
よろしくお願いいたします。
フレームサイズFsとオーバーラップ率overlapはメイン実行文で設定しています。
本記事では以下の数値がデフォルト値です。
Fs = 4096
overlap = 90
ここで、Fsを512, 124, 64…と小さくする場合やoverlapを98と大きな値にすると時間方向に細かくなりますが周波数方向が粗くなります。
逆に動かすと時間方向は粗くなりますが周波数方向が細かくなります。
データ点数によっては計算できない場合もありますが、是非色々いじってみてください。
ありがとうございます。
良いスペクトログラムが得られるようにいじってみようと思います。