ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
FFTのプログラムを書いていて、窓関数の必要性に気付いて使ってみると振幅レベルが理論値と異なるということに気付くと思います。今回はそんな理論との差を埋める「窓関数を使う場合の補正」について説明します。
こんにちは。wat(@watlablog)です。
はやくFFTしたい！と思って進めてみると意外と知らないことが沢山ありました。
今回は窓関数を使ったFFT時に必要となる「補正」を調べました！
窓関数補正の考え方
窓関数の利点と問題点を整理
WATLABブログでは以下の記事で窓関数について触れています。まずはそちらを参照頂けると、本記事の主旨が理解しやすくなると思います。
上記記事でも少し触れていますが、離散的なデータを扱う離散フーリエ変換はデータが周期的であることを仮定しています。
ハニング窓（ハン窓とも言う）等をかけることで、データフレーム内の両端がなめらかに0に向かい、FFTのノイズを軽減させたり不都合の解消をすることができるのが窓関数の利点です。
何も窓関数をかけない、つまりレクタンギュラウィンドウの場合と比べ、ハニング窓は両端のデータほど小さくなってしまうので、元の波形と比べ信号が小さくなってしまうというのが問題です。
窓関数で波形はどれくらい変わる？
ここでは最も代表的な窓関数であるハニング窓を使って検証していきたいと思います。
\(y(t)=Asin(2\pi ft)\)(\(f\)=100[Hz], \(A\)=1)の理想信号を使って時間波形とFFT波形をプロットしていきます。
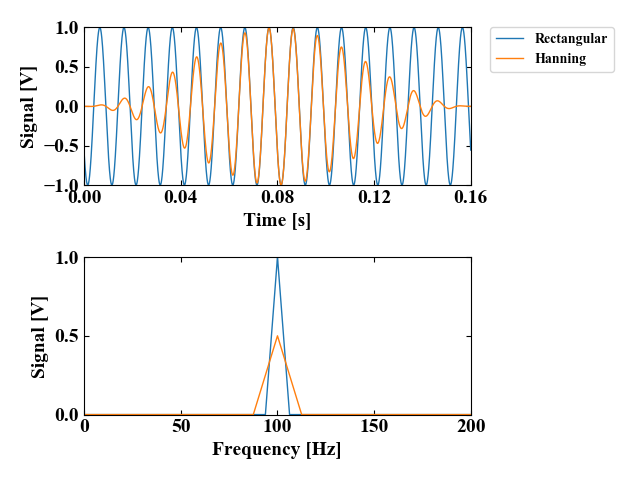
上の時間波形について、ハニング窓をかけた場合はデータフレームの両端が綺麗に0になっていき、中心部分はそのままという波形変化です。
下のFFT波形を見てみると、振幅が0.5になっている変化とともに、100Hzのピークの裾野が拡がっていることがわかります。
ちなみにピークの裾野の拡がりは窓関数の使用によって、周波数分解能が低下したことを意味するそうです。
元の信号では10Hzで1の振幅が、窓関数処理により、9Hzと11Hzに広がっていることがわかります。これは、周波数分解能が低下したことを意味します。
ソフトウェアクレイドル：窓関数の補正
振幅の低下は元の信号の半分になっており、これは窓関数の種類によっても変わってしまう要素なので、信号分析をする上で誤解の要因になりそうですね。
補正の考え方
補正を考えるために、一度ハニング窓の波形を見てみましょう。
ハニング窓はSciPyのsignal関数を使って作ります。フレームサイズ\(Fs\)は4096を設定しました。
|
1 2 |
from scipy import signal #SciPyパッケージからsignal関数インポート han = signal.hann(Fs) #ハニング窓の作成 |
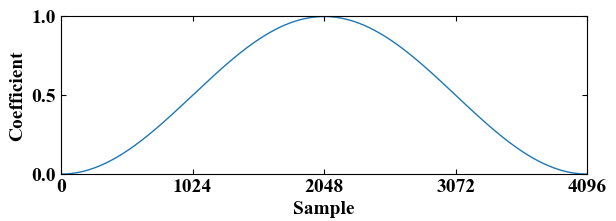
窓関数は基本的に縦軸の係数が0から1の範囲です。ハニング窓の場合は中心部から両端に向かって滑らかに0になっていきます。窓関数をかけない場合は係数が常に1であり、これはレクタンギュラ窓（矩形窓）をかけたことと同じ意味です。
補正はこの振幅が減ってしまった分を戻してあげることを考えれば良いので、窓関数の面積がレクタンギュラを1とした時と比べて何割になっているかを計算します。
理論式を積分すれば厳密な値が得られますが今回は離散データを対象にしているので、先ほど作成したハニング窓の波形を全て足して面積を求めフレームサイズで割った値を計算します。この計算でハニング窓がどれくらい矩形に比べて振幅が小さくなっているかが計算されましたので、後は逆数をとればFFT時の補正に使う係数として完成します。
|
1 2 3 4 |
acf = 1/(sum(han)/Fs) print(acf) >>2.0004884004883956 |
計算結果としておよそ2という値が得られました。
ここで、この振幅補正に使う値はAmplitude Correction Factorと呼ばれるそうです。以下のソフトメーカのページを参考にしました。
Window correction factors are used to try and compensate for the effects of applying a window to data. There are both amplitude and energy correction factors.
Siemens PLM software:Window Correction Factors
窓関数補正を考慮したFFT
補正有無のFFT結果の比較
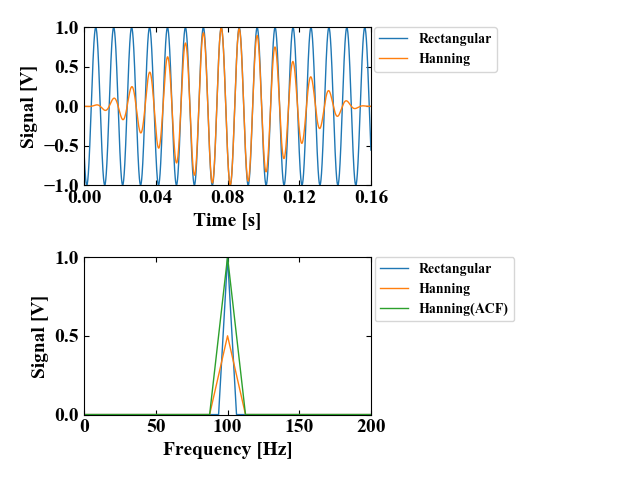
補正の効果を確かめるために、FFTをかけます。FFTに使うdataは100Hzのsin波で、4096ポイント分あります。以下のコード最終行でacfをかけ、補正を考慮したFFTを行います。
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np #NumPyインポート from scipy import signal #ハニング窓を使用するためにSciPyのsignalをインポート from scipy import fftpack ##FFTを使用するためにSciPyのfftpackをインポート Fs = 4096 #フレームサイズ han = signal.hann(Fs) #ハニング窓を作成 acf = 1/(sum(han)/Fs) #Amplitude Correction Factorを計算 fft_data_acf = acf*np.abs(fftpack.fft(data)/(Fs/2)) #dataは時間波形, FFT,正規化,振幅補正を実施 |
下の図が結果です。振幅補正を考慮したFFT波形（Hanning(ACF))はレクタンギュラ窓と振幅が一致しました。裾野の拡がりは窓関数によって周波数分解能が低下したことが原因とのことなので、フレームサイズを大きくすることで改善できそうです。後程検討して記事にしたいと思います。
まとめ
窓関数を使った場合は振幅や分解能に影響を与えることを学びました。
振幅は振幅補正を考慮することで改善可能です。今回はハニング窓で検証を行いましたが、基本的にはどんな窓関数を使っても考え方は同じなので、特殊な窓を使っても補正係数を自作することはできそうです。
窓関数って思ったより奥が深い。他にも信号がフレームの中で位相ずれした場合とかも後々調査したいですね。
こういう細かい話をしっかり理解しながら信号処理できればプロっぽいよね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント