人間は耳で音を聴く時、周波数によって聞こえ方が異なります。音は「聴感補正」をかけて人間の耳の聞こえ方に合わせた評価をすることが多々あります。ここでは一般にA特性と呼ばれる聴感補正曲線をPythonで作ります。
こんにちは。wat(@watlablog)です。
音の評価をする時は人間の耳に合わせたデータにすることが多々あります。この記事ではPythonで聴感補正（A特性）を実装する所までを解説します！
聴感補正の意味と式を理解しよう
聴感補正（A特性）とは？
聴感補正とはA特性補正とも呼ばれ、人間の耳における音の聞こえ方を模擬するために行う補正のことを意味します。
「Pythonで音圧のデシベル(dB)変換式と逆変換式」ではデシベルの話とともに、人間の耳の可聴音圧が20[μPa]～200[Pa]程度であると述べました。
音圧のレベルと同じく、音の周波数においても可聴周波数というものがあり、一般に人間は20[Hz]～20[kHz]の範囲でしか音を聴けないとされています。
年をとってくると、最大可聴周波数が20[kHz]からどんどん下がってきて耳が遠くなると言われるのは有名な話ですね。
僕(32)は13[kHz]くらいが限界かな。
聴くことのできる周波数がある範囲を持つといっても、実際はスパっと綺麗に聴こえなくなるわけではなく、最小可聴周波数や最大可聴周波数に近づくにつれ徐々に聴こえなくなってきます。
以下のグラフは聴感補正カーブです。記事の後半でPythonで算出するカーブとなります。
細かいことを言うと、人間は音の大きさによってさらに複雑な聴こえ方をするのですが、一般に国際規格で定められたA特性カーブというのはこの曲線を使います。
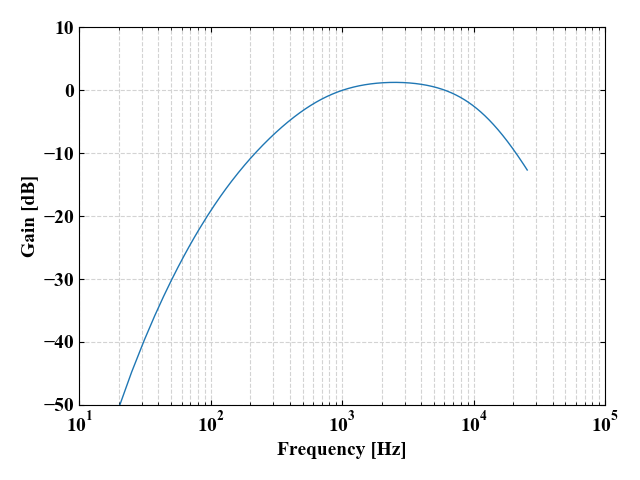
この波形は1[kHz]～6[kHz]で最も聴こえやすく、1[kHz]より下の低周波帯域は減衰が非常に大きく、20[Hz]以下ではゲインが-50[dB]を下回ります。
6[kHz]付近より上の高周波帯域でも減衰がかかったカーブとなっています。
補正式
上の聴感補正カーブの式を以下に示します。
$$R_{A}(f)= \frac{12194^{2}\cdot f^{4}}{(f^{2}+20.6^{2})\sqrt{(f^{2}+107.7^{2})(f^{2}+737.9^{2})}(f^{2}+12194^{2})}$$
$$A(f)= 20log_{10}(R_{A}(f))+2.00$$
各周波数\(f\)による\(R_{A}(f)\)をまず求め、次に最終的なA特性カーブ\(A(f)\)を求めるという流れです。この式は英語版のwikiにも載っています。
Pythonで聴感補正曲線を作ろう
補正式のPythonコード
以下がPythonで自作したA特性カーブの関数です。引数には周波数\(f\)を持ってきているので、上の式そのままの形で書くことができますね。
この引数\(f\)は単一の値でもNumPy配列でも入れることができるため、FFTをかけた後の周波数軸をそのまま入れても機能します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import numpy as np #聴感補正（A特性カーブ） def aweightings(f): if f[0] == 0: f[0] = 1e-6 else: pass ra = (np.power(12194, 2) * np.power(f, 4)) / \ ((np.power(f, 2) + np.power(20.6, 2)) * \ np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * \ (np.power(f, 2) + np.power(737.9, 2))) * \ (np.power(f, 2) + np.power(12194, 2))) a = 20 * np.log10(ra) + 2.00 return a |
FFTをかけた時の周波数軸は、大抵最初が0[Hz]で始まっています。A特性カーブの式で0[Hz]を代入すると分母が0になってしまい、0割のエラーが発生するので、if文でエラー回避させています。
\(R_{A}\)の式は長いので、バックスラッシュで行を分割していますが、1行で書いても動きます（あまり1行が長いとエラーになるかも？）。
動作確認
上記コードはA特性カーブを作る部分までの関数ですが、以下にそのまま実行してグラフ描画までができるコードを載せておきます。
お手持ちの環境で実行させてみて下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
import numpy as np from matplotlib import pyplot as plt #聴感補正（A特性カーブ） def aweightings(f): if f[0] == 0: f[0] = 1e-6 else: pass ra = (np.power(12194, 2) * np.power(f, 4)) / \ ((np.power(f, 2) + np.power(20.6, 2)) * \ np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * \ (np.power(f, 2) + np.power(737.9, 2))) * \ (np.power(f, 2) + np.power(12194, 2))) a = 20 * np.log10(ra) + 2.00 return a #ここからメイン f = np.linspace(0, 25600, 4096) # 周波数軸を作成 a = aweightings(f) # 周波数毎の聴感補正カーブを計算 # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Frequency [Hz]') ax1.set_ylabel('Gain [dB]') # スケールの設定をする。 ax1.set_xticks(np.arange(0, samplerate, 1000)) ax1.set_yticks(np.arange(-200, 200, 10)) ax1.set_xlim(10, 100000) ax1.set_ylim(-50, 10) ax1.set_xscale('log') plt.grid(which='major',color='lightgray',linestyle='--') plt.grid(which='minor',color='lightgray',linestyle='--') # データをプロットする。 ax1.plot(fft_axis, a, label='signal', lw=1) #重ならないための関数。 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
まとめ
人間の耳には可聴周波数というものがあり、ある範囲でしか音を聴くことができません。そしてその聴こえ方は聴感補正カーブで表現することができます。
聴感補正カーブはA特性カーブとも呼ばれ、式になっているので、このページではPythonを使って実装する所までを扱いました。
式になっていればどんな関数でも実装できるね！音の分析にはA特性をかけるのが一般的だから、この関数は多用しそうだ！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント