
数値流体力学の学習は各要素毎に離散化手法と解析手法を学ぶことが重要です。ここでは2次元の拡散方程式の概要や離散化手法を説明し、Pythonで実装しながら学習します。結果は定常解析の結果と比較することでラプラス方程式にも触れてみます。
こんにちは。wat(@watlablog)です。ここでは2次元の拡散方程式をPythonでコーディングする方法を紹介します!
おさらいと目標
1次元拡散方程式の数値計算
このブログでは「Pythonで拡散方程式を数値計算してアニメーションを作成する」の記事で1次元の拡散方程式を扱いました。
式(1)に1次元の拡散方程式を再掲します。
この式は時間項を含み、拡散係数\(\alpha\)によって決まる速度でスカラー物理量\(q\)が拡がっていくという意味を持ちます。この式を数値的に解くには先の記事に紹介した通り、境界条件の設定や安定条件を満たす必要があります。
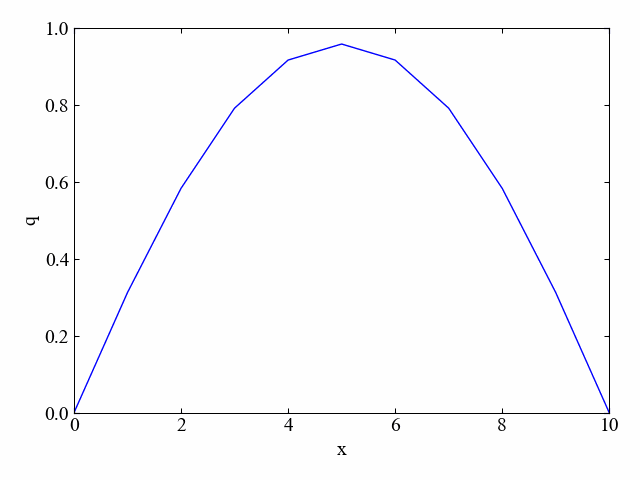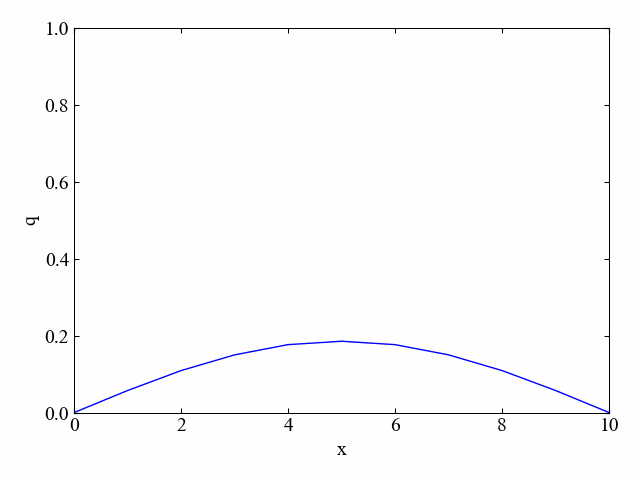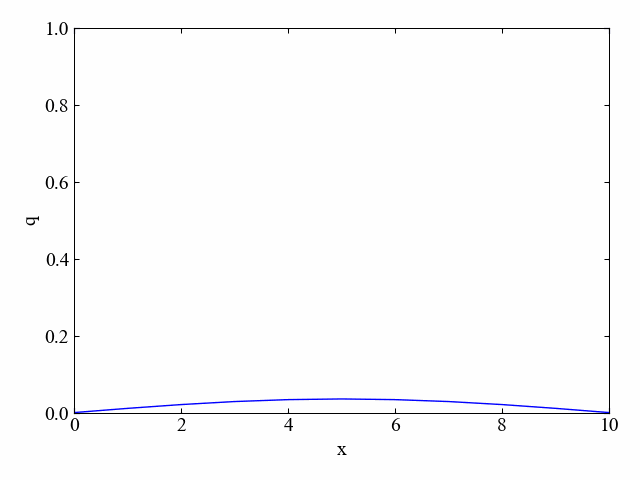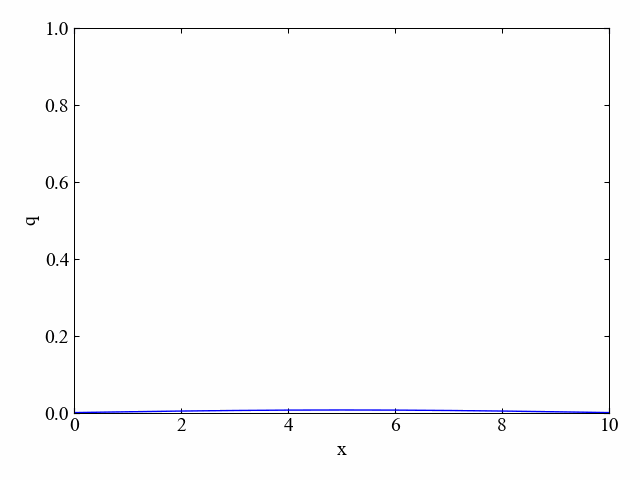
下図に結果例を示します。このように拡散方程式には次第に均一になろうとする特徴を持ちます。
拡散方程式の離散式を2次元に拡張してPythonで数値計算する
この記事では先ほどの1次元拡散方程式を2次元の問題に拡張し、Pythonによって数値計算する方法を習得することを目標とします。
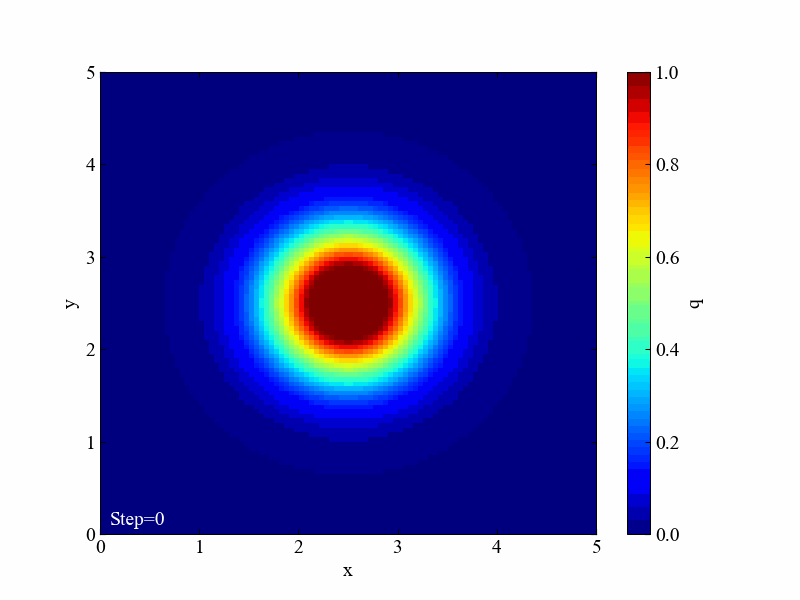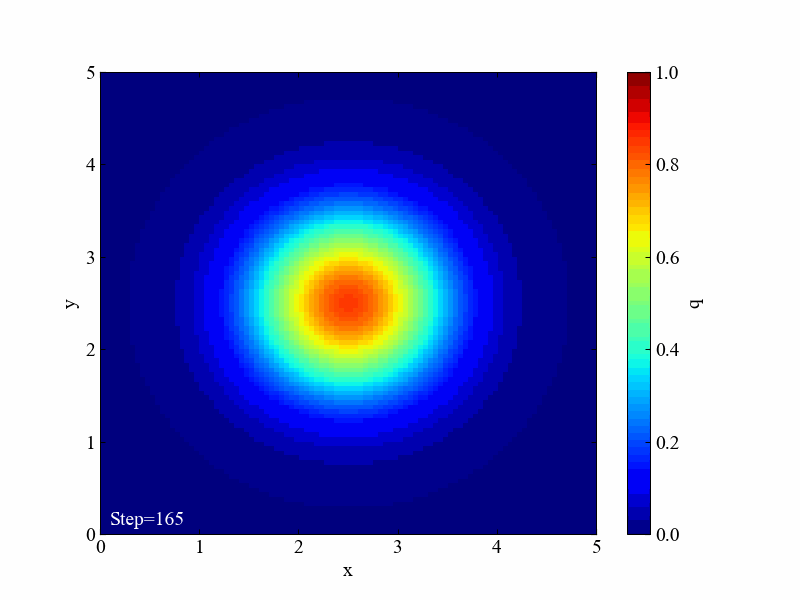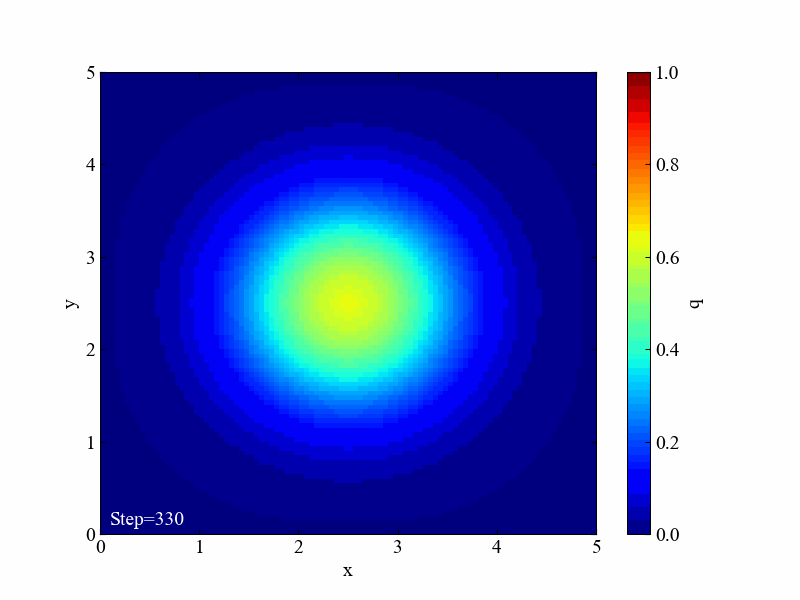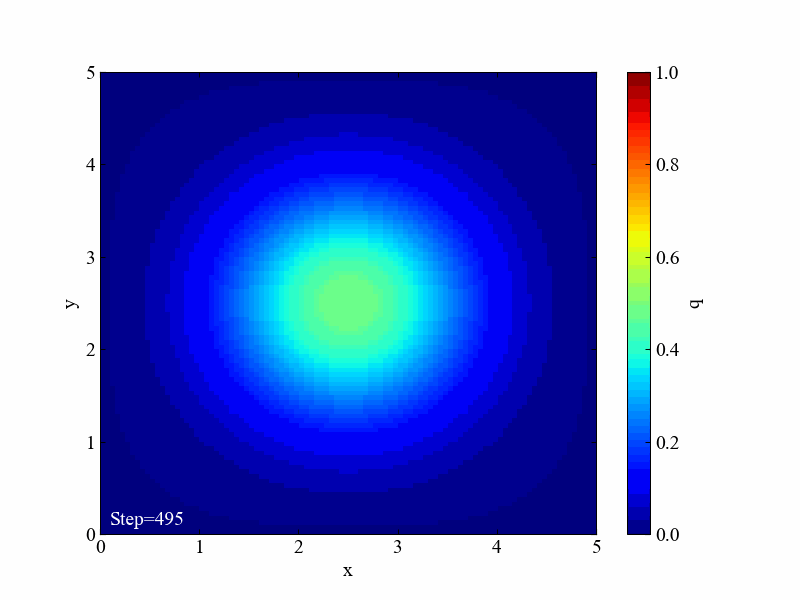
具体的には、本記事は2次元拡散方程式の数値計算結果から以下の動画をPythonで作ります。カラーマップ表示させることで、2次元においても均一になろうとする特性を確認できます。
Pythonで2次元拡散方程式の数値計算を実装するコード例
移流方程式の時と同様に、記事の最後にコピペ動作する全コードを紹介します。しかしその前に主要な要素を説明します。
ただしほとんどは「Pythonで2次元移流方程式を数値計算する方法」の記事で紹介したコードを流用するため、この記事は変化点のみを説明します。
動作環境
このページでは以下の環境で動作確認を行ったコードを掲載しています。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
| pillow | 7.1.2 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
計算格子/初期場
計算格子、初期場は先ほどの記事を流用します(格子サイズは変更します)。
計算格子は横軸を\(j\)、縦軸を\(k\)とします。
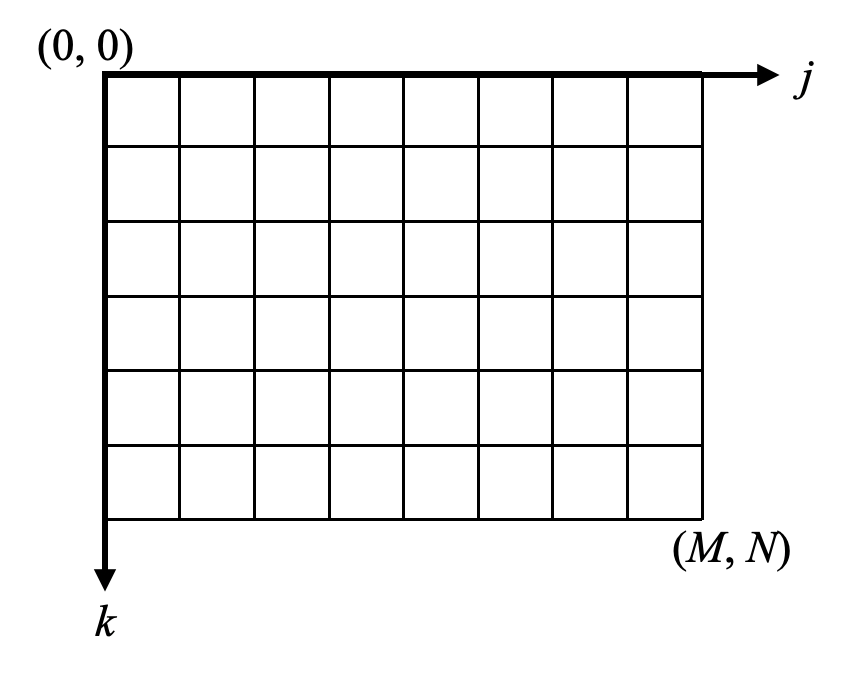
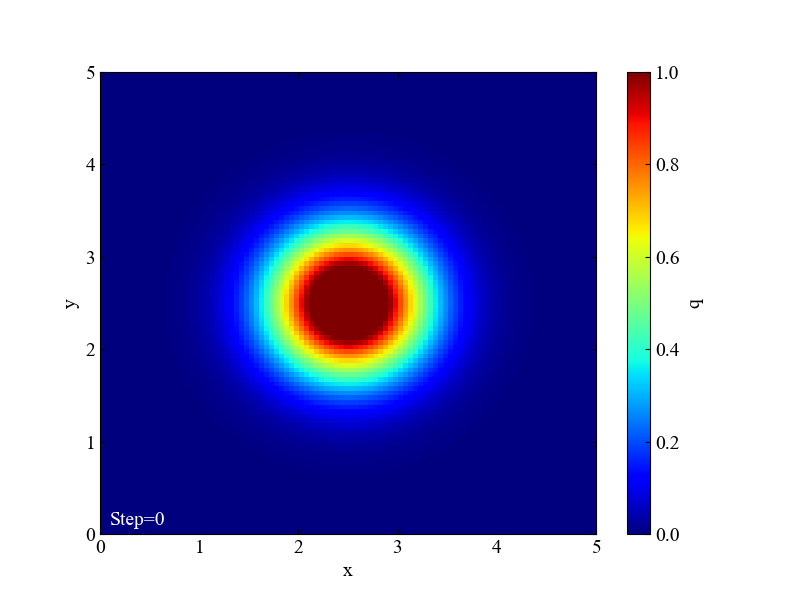
計算格子は5×5をそれぞれ0.05で分割した正方形とし、2次元のガウス関数を中心に配置しました。ガウス関数はこのような検証に使うのが便利な関数ですが、式も先ほどの記事に記載していますので是非ご確認ください。
境界条件
境界条件は4辺を0にするディリクレ条件とします。
|
1 2 3 4 5 |
# 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, :] = 0 z[-1, :] = 0 |
ソルバー(基礎方程式と離散化)
ここからが本題です。
式(2)に拡散方程式の基礎方程式を示します。ナブラ\(\nabla\)はおなじみの空間微分の作用素です。二乗しているのでラプラス作用素(ラプラシアン)とも呼びます。
ラプラシアンの入った偏微分方程式がどのような作用をするかは「Pythonで2次元ラプラス方程式を数値計算する方法」の記事をご参照ください。
式(2)は一般化されていますが、今回対象とする2次元空間\(\mathbb{R}^{2}\)について考えると式(3)となります。ここでは任意の物理量\(q\)が時間で拡散していくことを表現しており、拡散係数は熱伝導方程式をイメージして\(k\)を使っています。
コンピュータで数値計算するために式(3)を解くことができないため、式(4)と離散化します\(^{[1]}\)。この離散化方法については、空間差分はラプラス方程式を紹介した記事と同じ2次精度中心差分を使っています。
今回は以下のsol_2d_diffusion関数をソルバーとして書いてみました。forループを多用しているところは改善の余地ありですが、面倒なのでここではわかりやすさを優先します。
rとsは式(3)の中で安定性に関わる部分をまとめただけです。
2次元画像の配列を模擬した初期場を使いつつ、計算部分は式のj,kの順番とそろえるという観点から行列の転置を多用しています。。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
def sol_2d_diffusion(x, y, q, dt, dx, dy, a, step, dir, result_interval): ''' 2次元拡散方程式を計算する ''' # 漸化式を反復計算 q = q.T for i in range(step): q0 = q.copy() for j in range(1, len(q) - 1): for k in range(1, len(q.T) - 1): r = a * (dt / dx ** 2) s = a * (dt / dy ** 2) q[j, k] = q0[j, k] + r * (q0[j+1, k] - 2 * q0[j, k] + q0[j-1, k]) + \ s * (q0[j, k+1] - 2 * q0[j, k] + q0[j, k-1]) # 境界条件を設定 q = q.T q = boundary_condition(q) q = q.T # 指定した間隔で画像保存 if i % result_interval == 0: print('Iteration=', i) q = q.T plot(x, y, q, i, dir, 1) q = q.T return |
全コード(コピペ動作用)
以下にコピペ動作する全コードを紹介します。
2次元移流方程式の時とほぼ同じであるため、詳細説明はいらないと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 |
import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場(x方向をj, y方向をkとする行列を作成→2D画像のデータ構造を模擬) x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(y), len(x))) # 2D Gaussian(sigma:分散共分散行列, mu:平均ベクトル) sigma11 = 0.3 sigma22 = 0.3 sigma12 = 0 sigma21 = 0 mu_x = 2.5 mu_y = 2.5 sigma = np.array([[sigma11, sigma12], [sigma21, sigma22]]) mu = np.array([mu_x, mu_y]) det_sigma = np.linalg.det(sigma) inv_sigma = np.linalg.inv(sigma) # 式のj,kの順番と同じにするため転置させて計算する z = z.T for j in range(len(z)): for k in range(len(z.T)): X = np.array([x[j], y[k]]) z[j, k] = (1 / np.sqrt(2 * np.pi * det_sigma)) * np.exp((-1 / 2) * (X - mu).T @ inv_sigma @ (X - mu)) z = z.T return x, y, z def boundary_condition(z): ''' 分布に境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, :] = 0 z[-1, :] = 0 return z def sol_2d_diffusion(x, y, q, dt, dx, dy, a, step, dir, result_interval): ''' 2次元拡散方程式を計算する ''' # 漸化式を反復計算 q = q.T for i in range(step): q0 = q.copy() for j in range(1, len(q) - 1): for k in range(1, len(q.T) - 1): r = a * (dt / dx ** 2) s = a * (dt / dy ** 2) q[j, k] = q0[j, k] + r * (q0[j+1, k] - 2 * q0[j, k] + q0[j-1, k]) + \ s * (q0[j, k+1] - 2 * q0[j, k] + q0[j, k-1]) # 境界条件を設定 q = q.T q = boundary_condition(q) q = q.T # 指定した間隔で画像保存 if i % result_interval == 0: print('Iteration=', i) q = q.T plot(x, y, q, i, dir, 1) q = q.T return def plot(x, y, z, i, dir, save_flag): ''' 関数をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意して上下左右に目盛線を付ける。 x_size = 8 y_size = int(0.8 * x_size * (np.max(y) / np.max(x))) fig = plt.figure(figsize=(x_size, y_size)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 im = ax1.imshow(z, vmin=0, vmax=1, extent=[np.min(x), np.max(x), np.min(y), np.max(y)], aspect='auto', cmap='jet') ax1.text(0.1, 0.1, 'Step='+str(i), color="white") # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('q') # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) if save_flag == 1: # 画像を保存する plt.savefig(path) else: # グラフを表示する。 plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) imgs = [] # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=50, loop=0) return if __name__ == '__main__': ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する ''' # 画像保存フォルダと動画ファイル名 dir = 'img_2d_diffusion' filename = '2d-diffusion.gif' # 時間項の条件 dt = 0.0005 # 空間項の条件 dx = 0.05 dy = 0.05 x_max = 5 y_max = 5 # 初期場を用意する x, y, q = initial_field(x_max, y_max, dx, dy) #plot(x, y, q, 0, dir, 0) # 境界条件を設定する q = boundary_condition(q) plot(x, y, q, 0, dir, 0) # 拡散係数a a = 1 # 安定性の確認 nu_x = a * dt / dx ** 2 nu_y = a * dt / dy ** 2 print('nu_x, nu_y=', nu_x, nu_y) # 計算を実行 sol_2d_diffusion(x, y, q, dt, dx, dy, a, 500, dir, 5) # GIF動画を作成 create_gif(dir, filename) |
下図が実行後に生成されるGIF動画です。

ラプラス方程式の数値計算結果と比較する
実は(?)拡散方程式の時間項を省略すると最終的な定常状態・熱平衡状態を示すラプラス方程式になります。
ここでは「Pythonで2次元ラプラス方程式を数値計算する方法」の記事で紹介したラプラス方程式と同じ条件で比較することで結果を定性的に比較してみましょう。
先の記事では初期場を完全に0にして1辺だけが1になるようなディリクレ境界条件を付与していました。以下にその条件で書き換えた2次元拡散方程式の数値計算コードを示します。
まずはinitial_field関数からガウス関数の配置部分を排除します。
|
1 2 3 4 5 6 7 8 9 |
def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場(x方向をj, y方向をkとする行列を作成→2D画像のデータ構造を模擬) x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(y), len(x))) return x, y, z |
次にboundary_condition関数の上辺を1にします。
|
1 2 3 4 5 6 7 8 9 10 |
def boundary_condition(z): ''' 分布に境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, :] = 1 z[-1, :] = 0 return z |
時間で解く拡散方程式は定常状態になるまで時間がかかるので、ステップ数と画像の間引き数を変更して実行します。先ほどのコード実行時に作成されたimg_2d_diffusionフォルダを空にしておくことを忘れずに。
|
1 2 |
# 計算を実行 sol_2d_diffusion(x, y, q, dt, dx, dy, a, 1000, dir, 10) |
こちらが実行後に得られる動画です。1000ステップも計算しています。
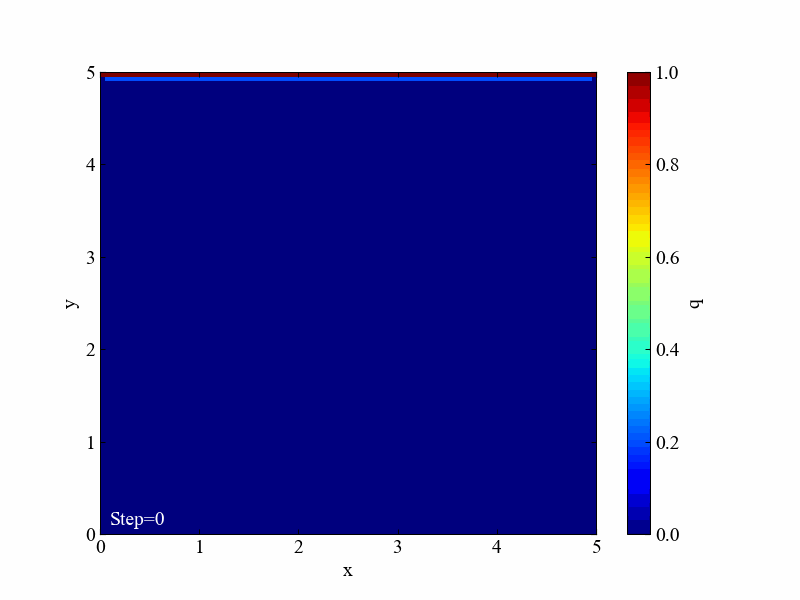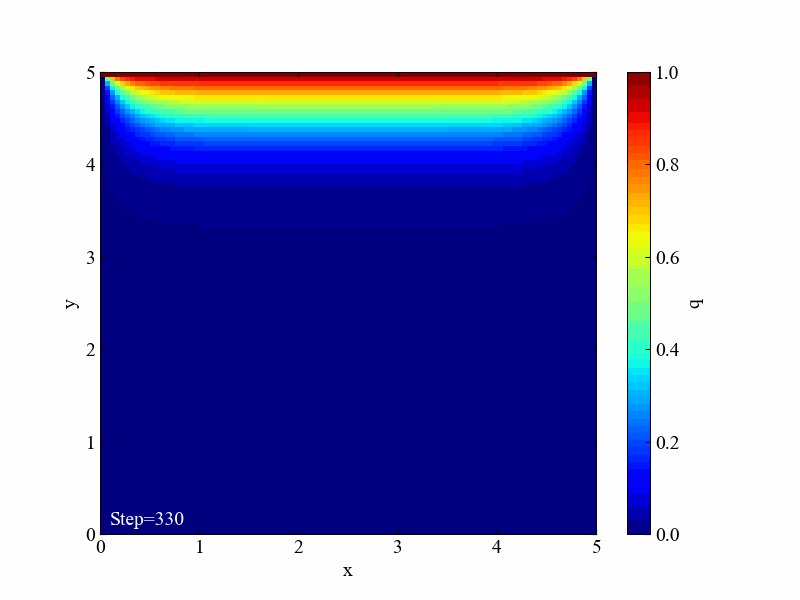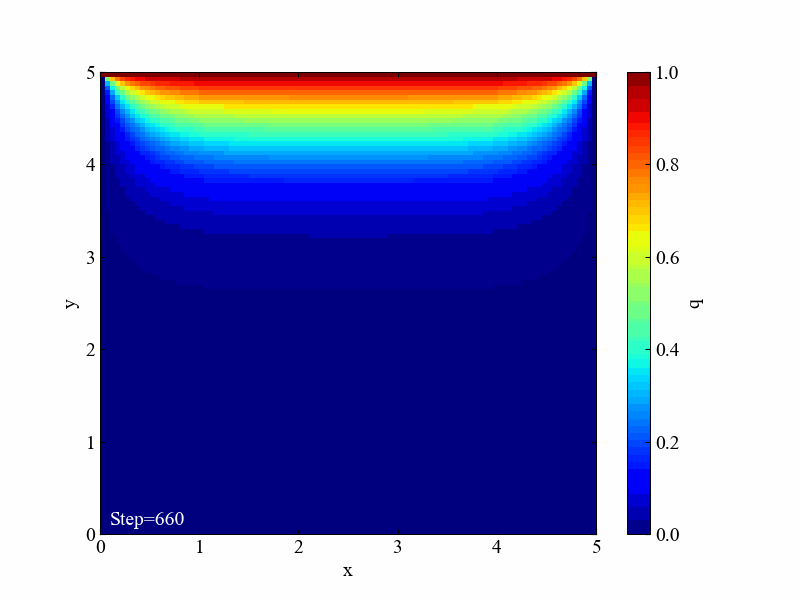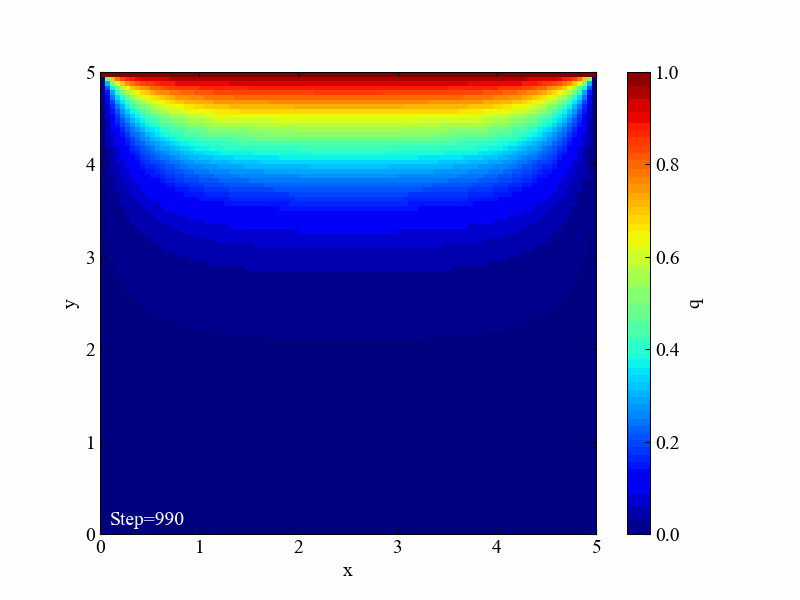
こちらがラプラス方程式の計算結果です。同条件と言いつつ格子最大サイズが1でしたね。ちなみにラプラス方程式は時間項を含まないので境界条件のみから計算結果が求まります。今回はSOR法という反復法で解いた結果を例にしました。
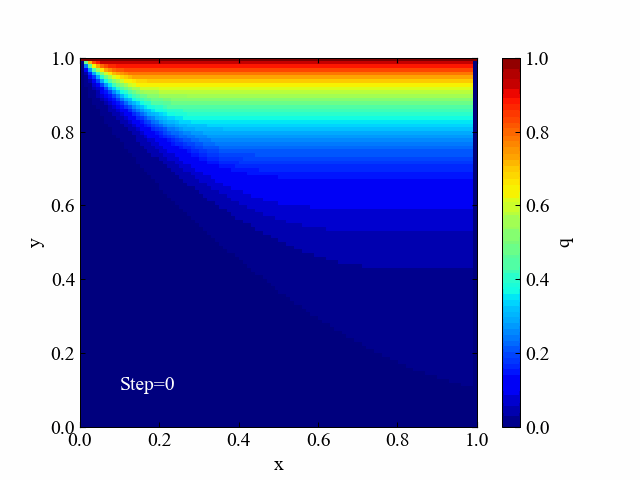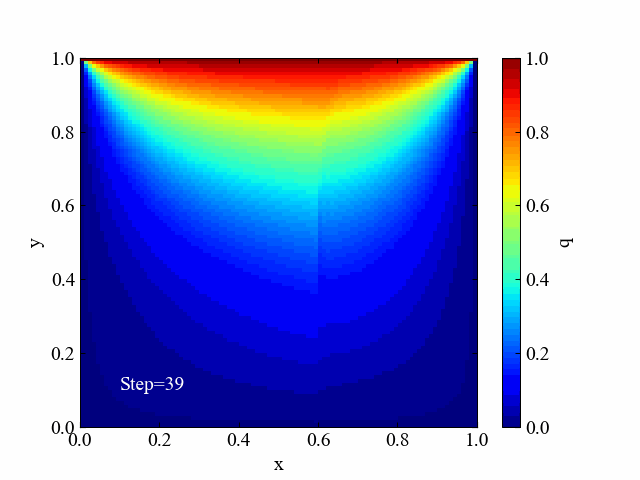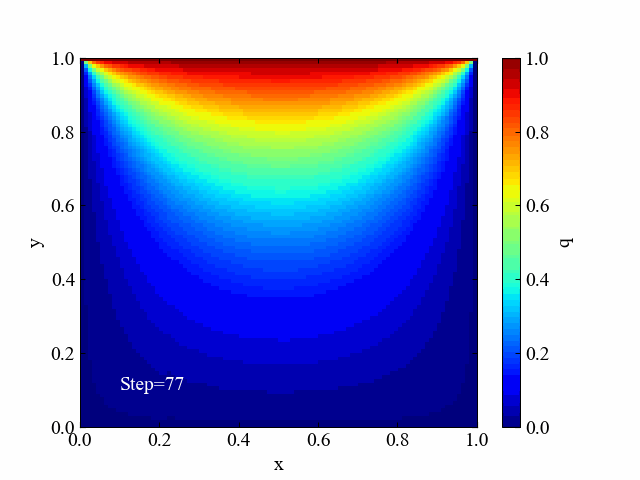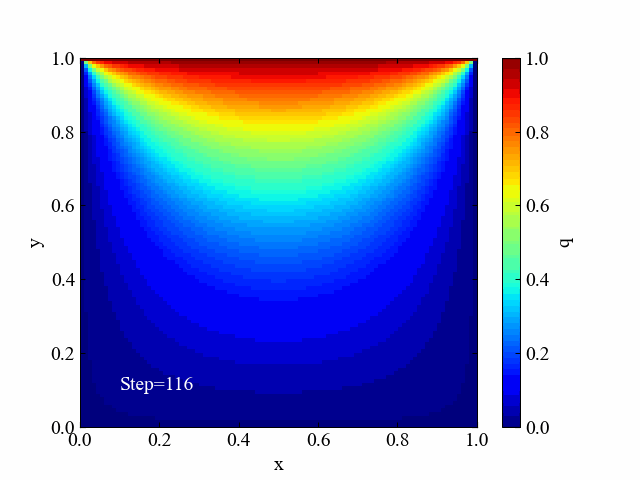
2つの結果を比較すると、拡散方程式の結果はまだまだ収束まで時間がかかりそうだとわかります。
2次元拡散方程式の数値計算が発散する例
最近は発散させる動画を示してオチとしているので、最後の2次元拡散方程式の発散例を示します。
最初に示した全コードに対して時間分解能dtを少々上げます。
|
1 2 |
# 時間項の条件 dt = 0.001 |
こちらが結果です。見事に発散しました。
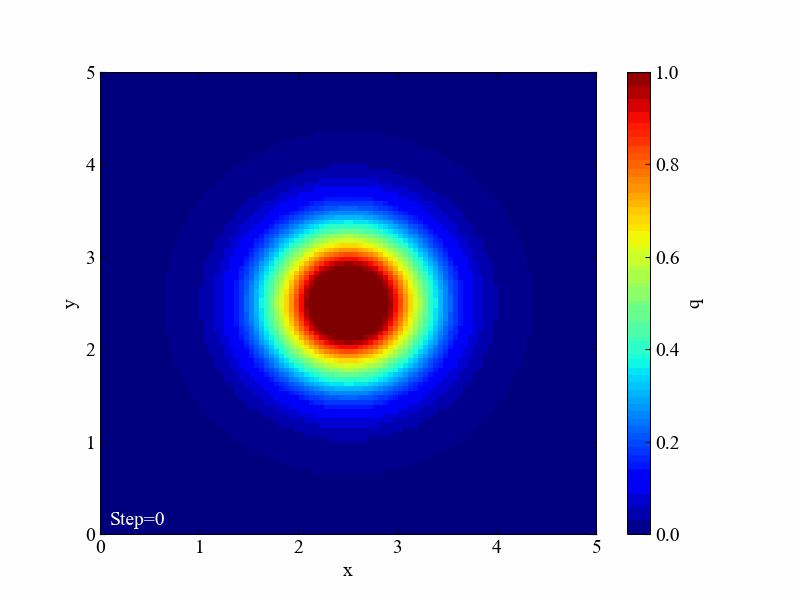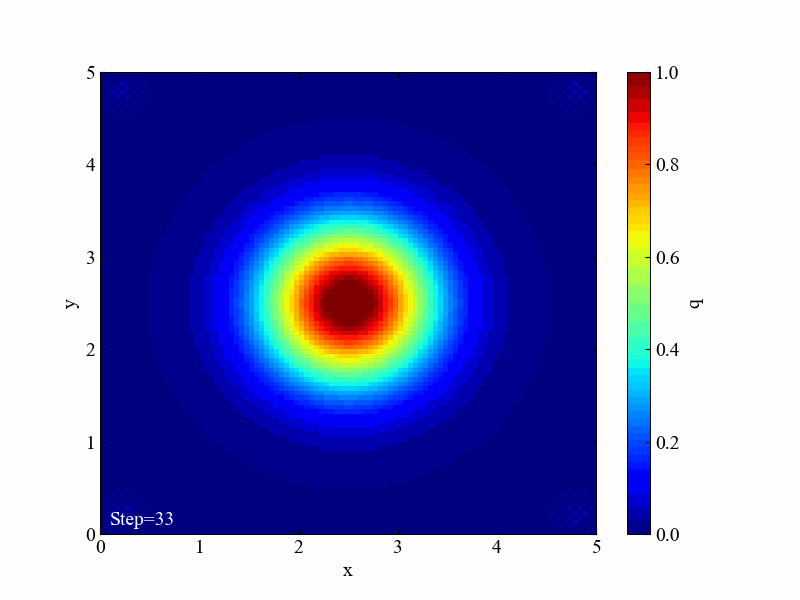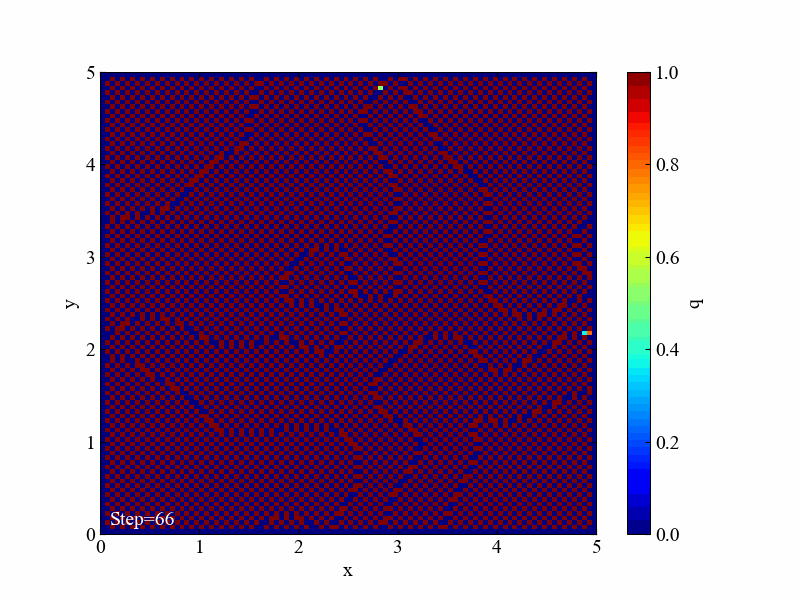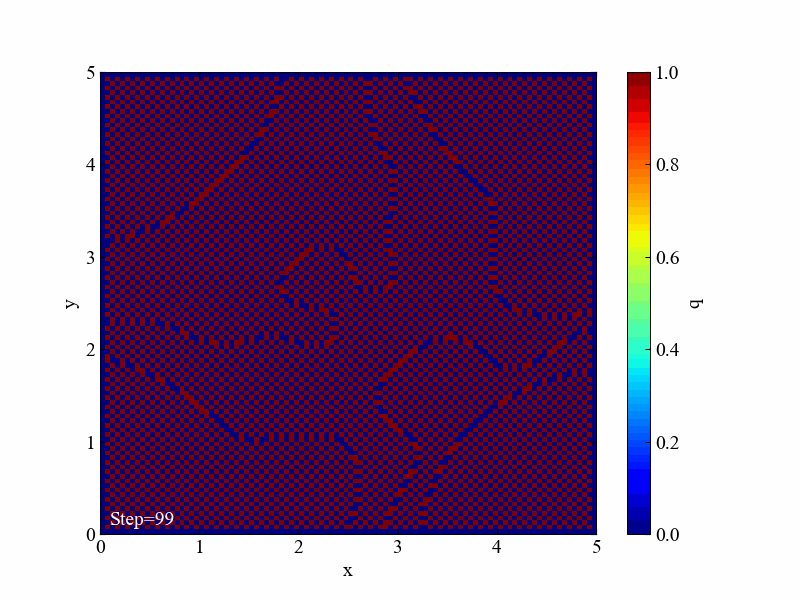
まとめ
この記事では2次元拡散方程式を学ぶためのおさらいとして、過去に紹介した1次元拡散方程式や2次元移流方程式、2次元ラプラス方程式の記事を参照しました。
各記事で行った離散化手法や2次元空間の計算方法を踏襲しただけなので、今回の記事で特に新しいことはありませんでした。
拡散方程式の結果はラプラス方程式の結果に近づくということも確認できました。
移流、拡散、定常状態…と個別の要素についてシミュレーションをしてきたので、次回は複合パターンを検討してみようと思います。
2次元移流に続き2次元拡散も数値計算できるようになりました!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!