
時間によって変化しない定常状態を示すラプラス方程式は様々な物理現象の基礎となっています。ここではラプラス方程式の差分化から説明します。また、学習の理解を深めるために簡単な2次元のラプラス方程式をPythonを使って数値計算する方法を紹介します。
こんにちは。wat(@watlablog)です。ここでは2次元のラプラス方程式を離散化して数値計算する方法を紹介します!
ラプラス方程式の概要
基礎方程式
ラプラス方程式(Laplace's Equation)とは、式(1)に表す楕円型偏微分方程式です。
ここで\(\phi\)は任意の物理量、\(\nabla ^{2}\)はラプラス作用素(Laplace operator)またはラプラシアン(Laplacian)と呼ばれ\(^{[1]}\)、空間2階微分を意味します。2次元空間\(\mathrm{R}^{2}\)であれば式(1)のラプラス方程式は式(2)と書くことができます。
この方程式は時間項が含まれていなく「定常状態または熱平衡状態」を表現しており、例えば境界に温度や電圧といったスカラー量が与えられた時、十分に時間が経過した後のスカラー分布を意味しています。
ラプラス方程式は電磁気学、流体力学、天文学といった様々な分野で多用されています。
今回筆者は計算力学技術者試験(熱流体)の学習でラプラス方程式を学んでいます。数値流体力学の分野ではナビエ・ストークス方程式の圧力項を解く時にこの方程式を扱います(実際にはラプラス方程式の右辺が0でないポアソン方程式を解きますが)。
ここではポアソン方程式を学ぶ前に、より簡単なラプラス方程式の数値解析方法を確認します。
離散化
テイラー展開を使って2次精度中心差分式を作る
この記事では式(2)の2次元ラプラス方程式を例に数値計算を行います。
数値計算は既に以下の記事で扱ったように、離散化が必要です。
・Pythonで1次元移流方程式を離散化して数値流体力学に入門する
・Pythonで拡散方程式を数値計算してアニメーションを作成する
式(2)は空間項のみで構成されており、先の拡散方程式と同様に2次精度中心差分で離散化しましょう。
このような2変数の方程式でもやり方は同様です。まずは式(2)の中で\(x\)から考えます。
中心差分は前進方向と後退方向を求めれば良さそうです。
2変数で表す任意の物理量を\(q(x, y)\)として、\(x\)方向に\(\Delta x\)だけずらした位置の前進方向の物理量\(q(x+\Delta x, y)\)はテイラー展開すると式(3)と求めることができます。
同様に、後退方向の物理量\(q(x-\Delta x, y)\)は式(4)となります。式(3)と比べ奇数階微分項の符号が反転しています。
式(3)と式(4)を加算すると、式(5)を得ます。ここで\(O((\Delta x)^{2})\)としたのは、2次以降の項を打ち切ったことを意味します。
式(5)の2階微分項を左辺、それ以外を右辺に移項し誤差項を省略して体裁を整えると、式(6)を得ます。この式が\(x\)方向の2次精度中心差分方程式です。
\(y\)方向も同様に計算すると式(7)を得ます。
ここまでの考え方で得た式(6)と式(7)を式(2)に代入すると、求めたい2次元ラプラス方程式の離散化形式を式(8)と得ることができます。
格子で考える
式(8)でも良いのですが、数値流体力学の一般的な格子点の座標表記に変換します。格子のイメージは下図です。\(i\)はプログラミングでよく使うので\(j, k\)としてみました。
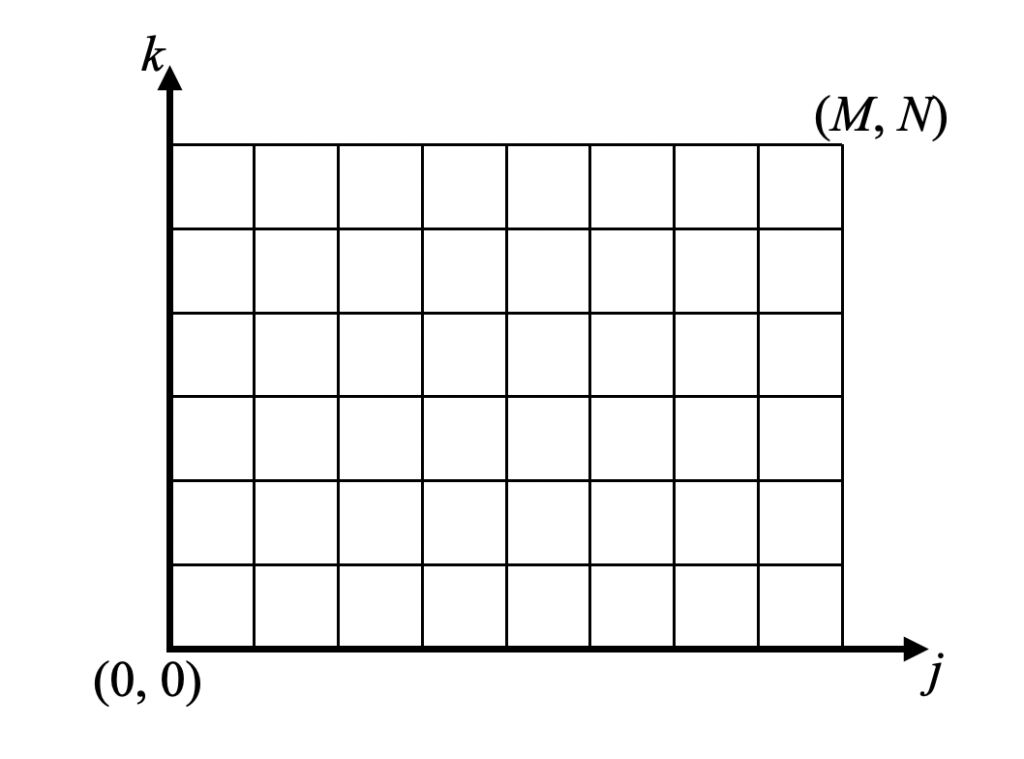
式(9)に格子点座標\(j, k\)で表現したラプラス方程式の2次精度中心差分方程式を示します。
漸化式
これまでの数値計算と同様に、漸化式を作って反復計算によりラプラス方程式の解を求めます。式(9)の\(q_{j, k}\)を左辺、それ以外を右辺にまとめることで式(10)の漸化式を得ます(演算自体は簡単ですが、結構面倒な計算かも)。
ここで、式(10)は全て同時間ステップの値のみを使います。このようにラプラス方程式の漸化式は同一時刻における格子点の情報のみを使って反復計算を行うことで、分布を収束させる式となりました。
反復法による解法
式(10)の漸化式は同一時刻の情報のみを使って値を収束させていく形式となりましたが、式(10)は格子点の数(\((M-1) \times (N-1)\))分の連立方程式ができあがります。
多元連立方程式を反復法で解く方法として、当ブログで扱ったヤコビ法、ガウス・ザイデル法、SOR法が使えます。このページではその比較もしてみましょう。
それぞれの手法は以下の記事にまとめています。
・Pythonで連立方程式をヤコビ法(反復法)で解く方法
・Pythonで連立方程式をガウス・ザイデル法(反復法)で解く方法
・連立方程式をSOR法で解くPythonコードと緩和係数のパラスタ
ここではそれぞれの手法における2次元ラプラス方程式の漸化式を示します。
ヤコビ法
式(11)に2次元ラプラス方程式をヤコビ法で解く場合の漸化式を示します。
添字\(n\)はステップ数を意味しています(時間ステップではありません)が、次のステップ\(n+1\)を更新するのに現在のステップ\(n\)のみを考慮するのが特徴です。また、 ヤコビ法は並列計算ができる手法でもあります。
ガウス・ザイデル法
式(12)に2次元ラプラス方程式をガウス・ザイデル法で解く場合の漸化式を示します。
ヤコビ法の右辺が全て\(n\)ステップ目の情報を使って漸化式を更新しているのに対し、ガウス・ザイデル法は既に求まった値(ここでは後退差分部分)を最新の値である\(n+1\)ステップ目の値を使って効率よく計算をしている特徴があります。
ガウス・ザイデル法はヤコビ法より少ない回数で収束に向かいますが、並列計算ができないというデメリットを持ちます。
SOR法
式(13)に示すSOR法(Successive Over-Relaxation Method)は緩和係数\(\omega\)を使ってガウス・ザイデル法よりもさらに少ない回数で収束させようという手法です。基本的にはガウス・ザイデル法と同じ考え方のため、並列計算はできません。
SOR法の記事では、ヤコビ法の反復行列のスペクトル半径を行列から求めて最適な緩和係数\(\omega_{opt}\)を算出していましたが、格子サイズ\((m, n)\)がわかっている場合は式(14)でも求められるようです\(^{[2]}\)。
初期場と境界条件
ラプラス方程式は任意の計算領域(ドメイン)の中を反復計算します。そのため計算領域の端である境界には境界条件(Boundary condition)が必要です。また、計算開始時には初期場(Initial field)として初期化(Initialization)も必要です。
今回は1辺が1の正方行列を100×100格子で用意し、上辺に境界条件1、それ以外の3辺に0を与えました。そして境界以外の格子の値を0で初期化した条件を例にラプラス方程式を数値的に解いていきます。
以下はmatplotlibによるプロットの例です。ちなみに配列の表現はNumPyのスライス記法です。
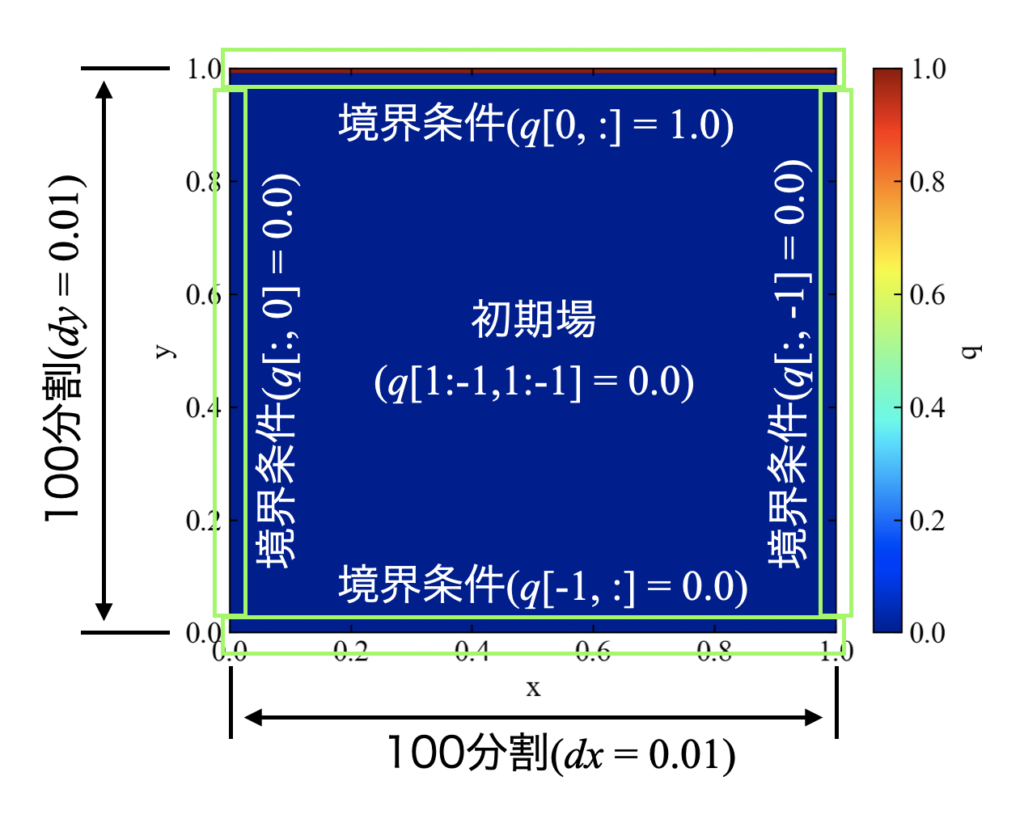
Pythonで2次元ラプラス方程式を解くコード
動作環境
このページでは以下の環境で動作確認を行ったコードを掲載しています。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
ヤコビ法のコード
それではいよいよ2次元ラプラス方程式を数値計算で解くPythonコードを書いてみましょう。まずはヤコビ法の場合の全コードを以下に示します。
コードの構成としては、通常のシミュレーションソフトウェアをイメージして「初期場の設定」「境界条件の設定」「ソルバー」「ポスト処理(結果の可視化)」という要素に分けて関数化しています。
コメント部分を順番に追って確認すればどのように計算しているかがわかると思います。今回は学習目的であり、式をそのまま書けるわかりやすさからダブルforループを書いていますのでプログラム実行速度は遅いです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 |
import numpy as np from matplotlib import pyplot as plt import time def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場 x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(x), len(y))) return x, y, z def boundary_condition(z): ''' 分布に境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, :] = 1 z[-1, :] = 0 return z def sol_2d_laplace(dx, dy, z, tolerance): ''' 2次元ラプラス方程式を解く ''' # 初期化 z0 = z.copy() residual = 1e20 # 反復計算=>残差がトレランスより小さくなったら終了 t0 = time.time() i = 0 print('----------Start iteration----------') while residual > tolerance: # 未知数を計算 for j in range(1, len(z) - 1): for k in range(1, len(z.T) - 1): z[j, k] = ((dy ** 2) * (z0[j+1, k] + z0[j-1, k]) + (dx ** 2) * (z0[j, k+1] + z0[j, k-1])) \ /(2 * (dx ** 2 + dy ** 2)) # 境界条件を設定 z = boundary_condition(z) residual = np.sum(np.sqrt((z - z0) ** 2)) / np.sum(np.sqrt(z ** 2)) if i % 100 == 0: print('Iteration=', i) print('Residual=', residual) i += 1 z0 = z.copy() t1 = time.time() print('----------End iteration----------') print('Iteration=', i) print('Residual=', residual) print('Elapsed time[s] =', float(t1 - t0)) return z def plot(x, y, z): ''' 関数をプロットする ''' X, Y = np.meshgrid(x, y) # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意して上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 im = ax1.imshow(z, vmin=np.min(z), vmax=np.max(z), extent=[np.min(x), np.max(x), np.min(y), np.max(y)], aspect='auto', cmap='jet') # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('q') # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': # 計算領域(範囲と分解能)を設定 x_max = 1 y_max = 1 dx = 0.01 dy = 0.01 # 初期場を設定 x, y, z = initial_field(x_max, y_max, dx, dy) # 境界条件を設定 z = boundary_condition(z) # ラプラス方程式を解く z = sol_2d_laplace(dx, dy, z, 1e-4) # ポスト処理 plot(x, y, z) |
下図が結果です。よく見るラプラス方程式の結果がコンター図で確認できました。
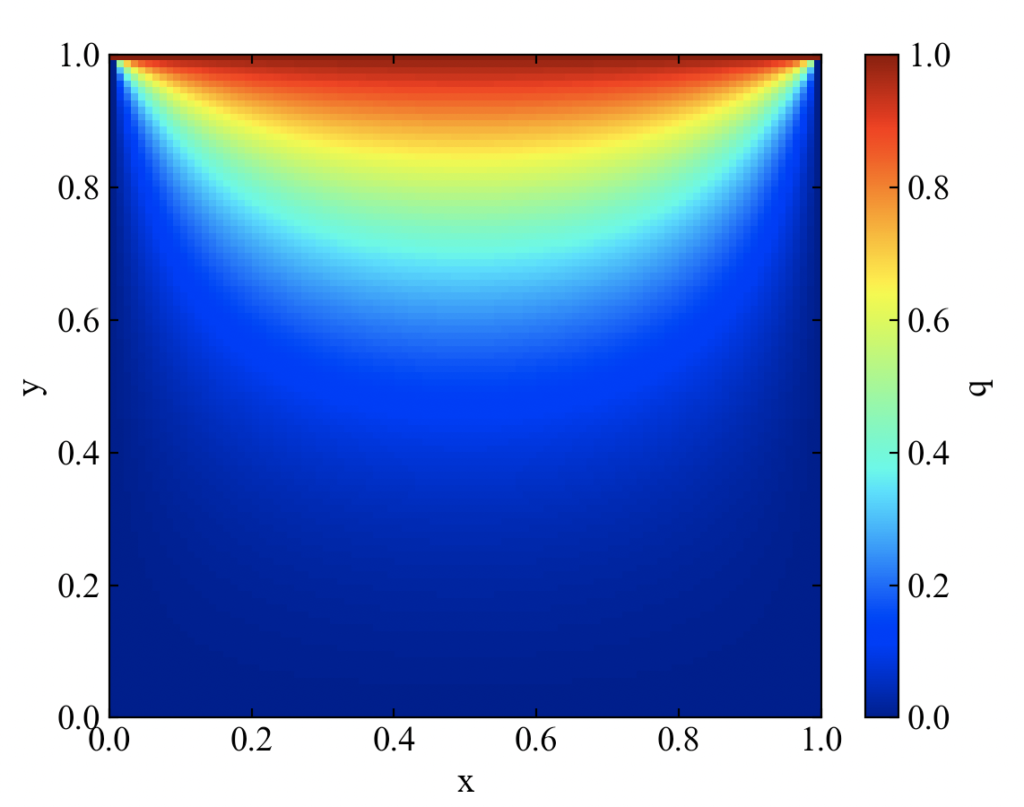
プログラムは実行中に反復回数であるIterationをカウントしています。このプログラムではなんと2704回の反復回数を約34秒もかけて実行していました。反復回数はヤコビ法のアルゴリズム起因ですが、かかっている実行時間は単純にコーディングしたPythonのforループの遅さが目立っている結果と思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
----------Start iteration---------- Iteration= 0 Residual= 0.19678714859437751 Iteration= 100 Residual= 0.004222928855605138 Iteration= 200 Residual= 0.0021158807445434617 Iteration= 300 . . . ----------End iteration---------- Iteration= 2704 Residual= 9.993980124076538e-05 Elapsed time[s] = 33.706843852996826 |
ガウス・ザイデル法のコード
続いて式(12)のガウス・ザイデル法のコードを以下に示します。ソルバー部分のみを書いています。古い分布を保持していますが計算のためではなく、収束計算のためです。その他は全て先ほどのコードと同様です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
def sol_2d_laplace(dx, dy, z, tolerance): ''' 2次元ラプラス方程式を解く ''' # 初期化 z0 = z.copy() residual = 1e20 # 反復計算=>残差がトレランスより小さくなったら終了 t0 = time.time() i = 0 print('----------Start iteration----------') while residual > tolerance: # 未知数を計算 for j in range(1, len(z) - 1): for k in range(1, len(z.T) - 1): z[j, k] = ((dy ** 2) * (z[j+1, k] + z[j-1, k]) + (dx ** 2) * (z[j, k+1] + z[j, k-1])) \ /(2 * (dx ** 2 + dy ** 2)) # 境界条件を設定 z = boundary_condition(z) residual = np.sum(np.sqrt((z - z0) ** 2)) / np.sum(np.sqrt(z ** 2)) if i % 100 == 0: print('Iteration=', i) print('Residual=', residual) i += 1 z0 = z.copy() t1 = time.time() print('----------End iteration----------') print('Iteration=', i) print('Residual=', residual) print('Elapsed time =', float(t1 - t0)) return z |
結果は以下です。1930回の反復回数で約25秒でした。約1.4倍の速度UPができたようです(それでも遅いけど)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
----------Start iteration---------- Iteration= 0 Residual= 0.3277310924369749 Iteration= 100 Residual= 0.004106685272206501 Iteration= 200 Residual= 0.002016243694152434 . . . ----------End iteration---------- Iteration= 1930 Residual= 9.995246091880695e-05 Elapsed time = 25.157893896102905 |
SOR法のコード
最後は式(13)のSOR法で数値計算してみます。
先ほどと同様にソルバー部分のみのコードを示します。式(14)の最適な緩和係数を使って解くとどれだけはやくなるのでしょうか。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
def sol_2d_laplace(dx, dy, z, tolerance): ''' 2次元ラプラス方程式を解く ''' # 初期化 z0 = z.copy() residual = 1e20 # 最適な緩和係数を推定 m = len(z) n = len(z.T) rho = (np.cos(np.pi / m) + np.cos(np.pi / n)) / 2 omega_opt = 2 / (1 + np.sqrt(1 - rho ** 2)) # 反復計算=>残差がトレランスより小さくなったら終了 t0 = time.time() i = 0 print('----------Start iteration----------') while residual > tolerance: # 未知数を計算 for j in range(1, len(z) - 1): for k in range(1, len(z.T) - 1): z[j, k] = (1 - omega_opt) * z[j, k] + omega_opt * \ ((dy ** 2) * (z[j+1, k] + z[j-1, k]) + (dx ** 2) * (z[j, k+1] + z[j, k-1])) \ / (2 * (dx ** 2 + dy ** 2)) # 境界条件を設定 z = boundary_condition(z) residual = np.sum(np.sqrt((z - z0) ** 2)) / np.sum(np.sqrt(z ** 2)) if i % 100 == 0: print('Iteration=', i) print('Residual=', residual) i += 1 z0 = z.copy() t1 = time.time() print('----------End iteration----------') print('Iteration=', i) print('Residual=', residual) print('Elapsed time =', float(t1 - t0)) return z |
目を疑うほどの結果を得ました!SOR法はヤコビ法と比べ反復回数で23倍、計算速度で18倍ほどの速度向上効果を得ました。
Pythonでforループを使っていますが体感時間的にもストレスを感じません。もっと大きい行列でもノートPCによる計算ができそうです。
|
1 2 3 4 5 6 7 8 9 |
----------Start iteration---------- Iteration= 0 Residual= 0.9289314115967969 Iteration= 100 Residual= 0.0002457984664039389 ----------End iteration---------- Iteration= 117 Residual= 9.727472048558602e-05 Elapsed time = 1.8675272464752197 |
ヤコビ法で2704回、ガウス・ザイデル法で1930回かかる計算がSOR法で117回とは…!おそるべしアルゴリズムの効果!
おまけ:収束仮定をアニメーションで確認してみる
ヤコビ法の収束過程動画
せっかくなので、当ブログ恒例の動画作成による可視化を行ってみましょう。
(コードは最後)
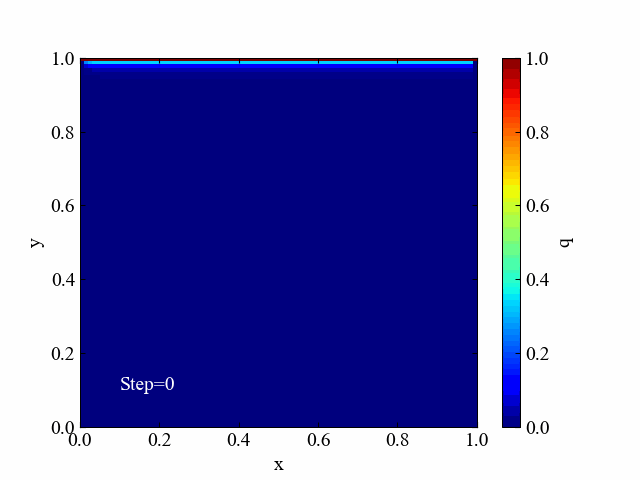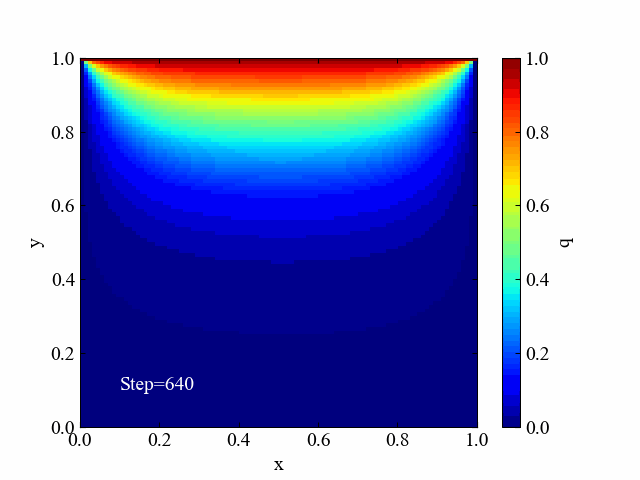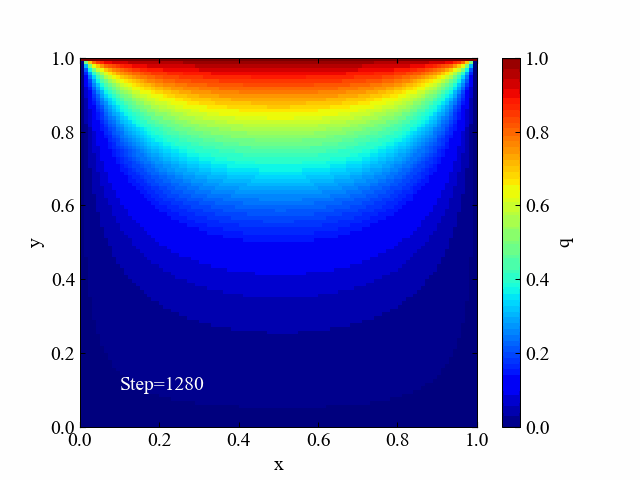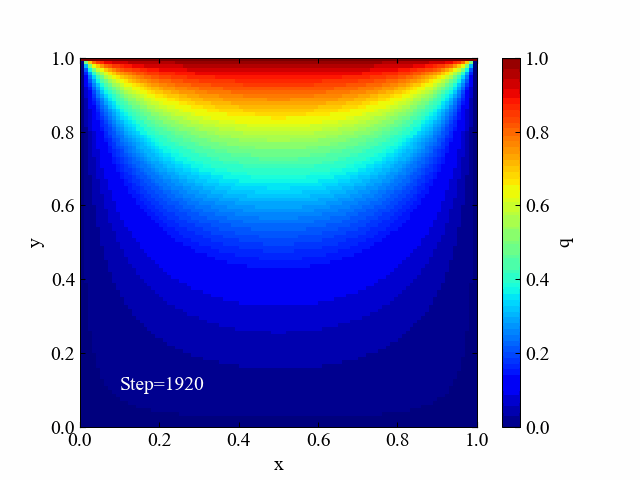
こちらはヤコビ法による反復計算中の解分布を可視化した動画です。ゆっくりと境界条件の値が伝播しているのがよくわかりますね。
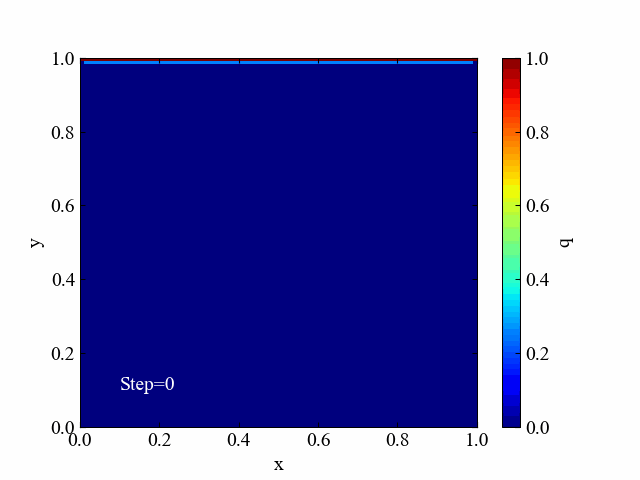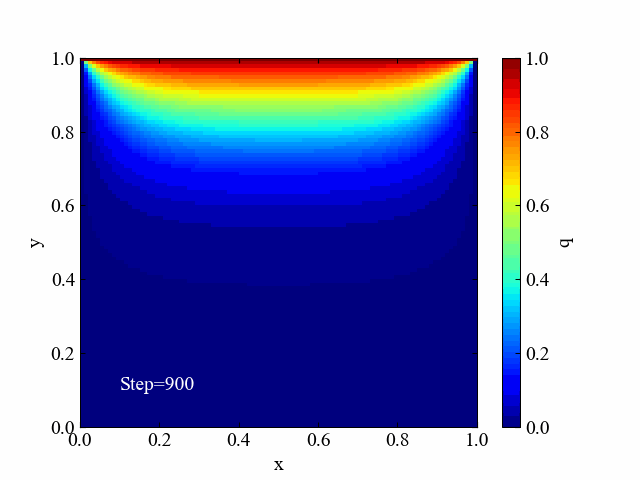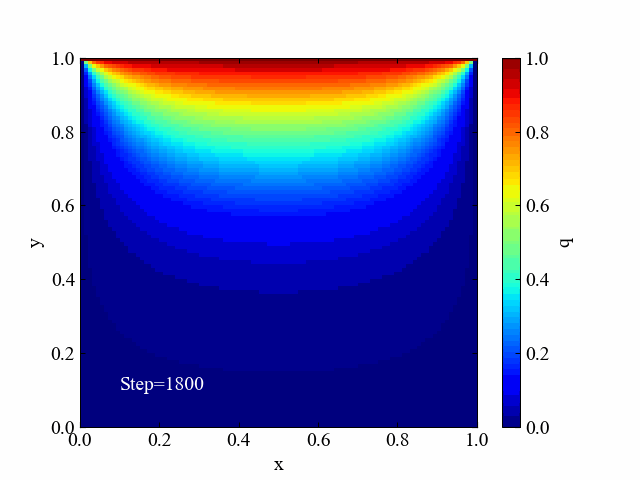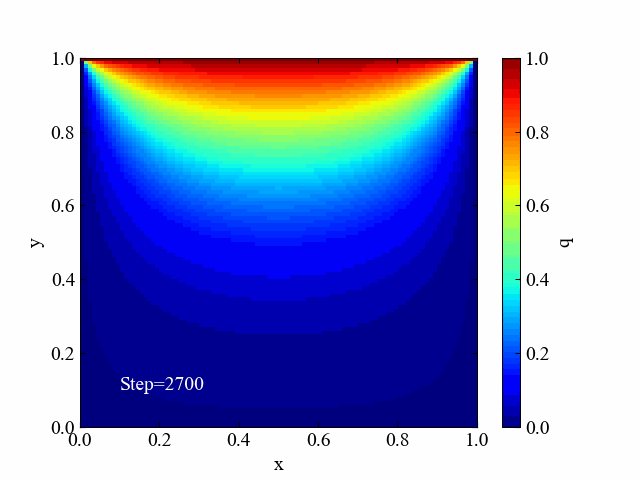
ガウス・ザイデル法の収束過程動画
ガウス・ザイデル法の場合はこちら。動画のステップ数を先ほどより多めの20刻みにしていますが、基本的にはヤコビ法と同じような解変化をしていることがわかりました。
SOR法の収束過程動画
続いてSOR法の場合の動画です。こちらは何か間違ったか、と思うほど解の変化傾向が異なりました。端っこからどんどん最終形態に近づいていっている様子が面白いです。
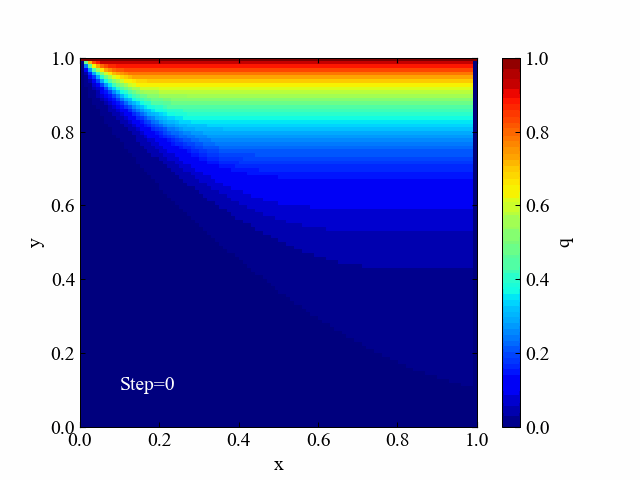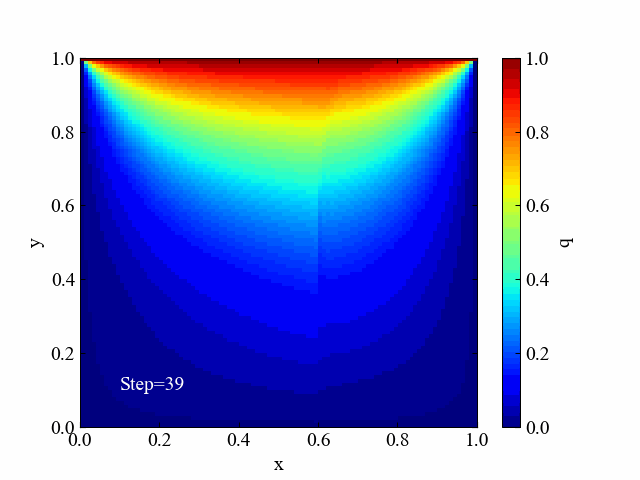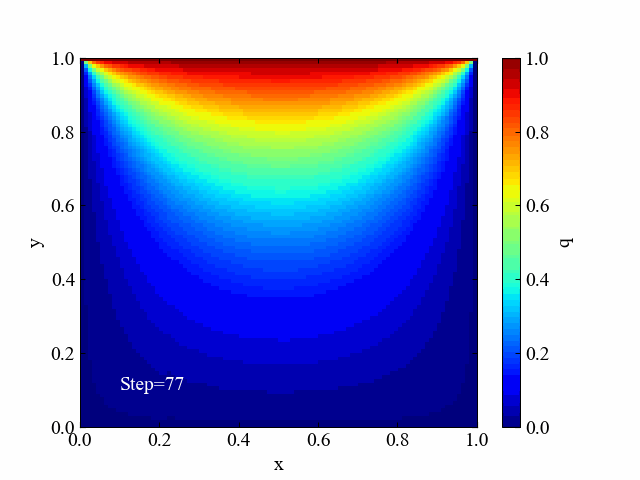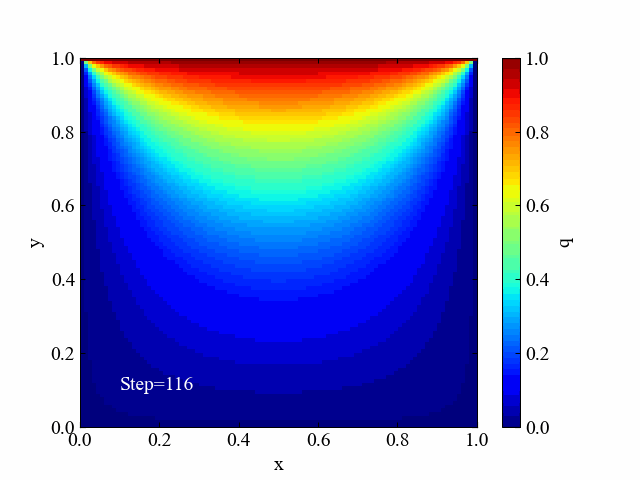
SOR法の場合のみ動画作成を含む全コードを紹介しておきます。是非お好みの境界条件を作ったりして遊んでみてください(境界条件は辺以外にもつくることができますよ!)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
import numpy as np from matplotlib import pyplot as plt import time from PIL import Image import os import glob def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0) return def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場 x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(x), len(y))) return x, y, z def boundary_condition(z): ''' 分布に境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, :] = 1 z[-1, :] = 0 return z def sol_2d_laplace(dx, dy, z, tolerance): ''' 2次元ラプラス方程式を解く ''' # 初期化 z0 = z.copy() residual = 1e20 # 最適な緩和係数を推定 m = len(z) n = len(z.T) rho = (np.cos(np.pi / m) + np.cos(np.pi / n)) / 2 omega_opt = 2 / (1 + np.sqrt(1 - rho ** 2)) # 反復計算=>残差がトレランスより小さくなったら終了 t0 = time.time() i = 0 print('----------Start iteration----------') while residual > tolerance: # 未知数を計算 for j in range(1, len(z) - 1): for k in range(1, len(z.T) - 1): z[j, k] = (1 - omega_opt) * z[j, k] + omega_opt * \ ((dy ** 2) * (z[j+1, k] + z[j-1, k]) + (dx ** 2) * (z[j, k+1] + z[j, k-1])) \ / (2 * (dx ** 2 + dy ** 2)) # 境界条件を設定 z = boundary_condition(z) residual = np.sum(np.sqrt((z - z0) ** 2)) / np.sum(np.sqrt(z ** 2)) if i % 1 == 0: # ポスト処理 plot(x, y, z, i) print('Iteration=', i) print('Residual=', residual) i += 1 z0 = z.copy() t1 = time.time() print('----------End iteration----------') print('Iteration=', i) print('Residual=', residual) print('Elapsed time =', float(t1 - t0)) return z def plot(x, y, z, i): ''' 関数をプロットする ''' X, Y = np.meshgrid(x, y) # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意して上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 im = ax1.imshow(z, vmin=np.min(z), vmax=np.max(z), extent=[np.min(x), np.max(x), np.min(y), np.max(y)], aspect='auto', cmap='jet') ax1.text(0.1, 0.1, 'Step='+str(i), color="white") # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('q') # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = 'img-laplace2d' if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() if __name__ == '__main__': # 計算領域(範囲と分解能)を設定 x_max = 1 y_max = 1 dx = 0.01 dy = 0.01 # 初期場を設定 x, y, z = initial_field(x_max, y_max, dx, dy) # 境界条件を設定 z = boundary_condition(z) # ラプラス方程式を解く z = sol_2d_laplace(dx, dy, z, 1e-4) # GIFを保存する create_gif('img-laplace2d', 'laplace-2d-SOR.gif') |
まとめ
この記事は数値流体力学の中で、空間項のみで表されたラプラス方程式の概要を紹介しました。
ラプラス方程式は境界条件が決まると解が求まる楕円型偏微分方程式であることや、2次精度中心差分による離散化手法を説明しました。
式は一つ一つ丁寧に展開していったので、初学者にもやさしい内容になったのではと思っています(←)。
また、ここで紹介したラプラス方程式は連立方程式を反復法で解きましたが、当ブログで既に紹介したヤコビ法、ガウス・ザイデル法、SOR法の3手法の比較を行いました。
離散化式はそれぞれ似ていますが、3つの手法の中でSOR法が圧倒的にはやいということも確かめられ、さらに動画による違いも確認することができました。
ヤコビ法は並列計算ができ、その他はできないので一概にどの手法が優れているかは言えませんが、アルゴリズムで挙動が劇的に変わる様子を目の当たりにできたのは面白かったです。
(forループ使わない方法、筆者はまだヤコビ法しかかけない…。SOR法をforループ最低限版で書きたいですがまだ思いつきません。ダレカオシエテクダサイ…。)
参考文献
[1]:斎藤恭一, なっとくする偏微分方程式, 講談社, (2008), pp100 [2]:山崎郭滋, 偏微分方程式の数値解法入門, 森北出版,(2015), pp28ラプラス方程式を数値計算できました!2次元は可視化が派手で面白いですね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!