
1次元移流方程式で基礎を学んだ後は2次元移流方程式を学びます。ここでは2次元移流方程式の差分化手法の例とPythonコードによるアニメーション作成までを行います。2次元の初期場を作る方法、漸化式の更新方法、結果のプロット方法について考えてみた結果を紹介します。
こんにちは。wat(@watlablog)です。Pythonで2次元移流方程式の数値計算を行いアニメーションを作ってみます!
おさらいと目標
1次元移流方程式の数値計算
WATLABブログでは「Pythonで1次元移流方程式を離散化して数値流体力学に入門する」の記事で1次元の移流方程式を扱いました。
式(1)に1次元移流方程式を再掲しますが、詳しくは上の記事をご確認ください。
この方程式は時間項と空間項から成り、一定速度\(c\)であることから線形です。先の記事では、この式の厳密解が波形の形を変えないでスライドしていくことや、数値計算時にクーラン数を超えてはならないということを紹介しました。また、差分化の方法にも色々な手法があることもまとめています。
下図に1次元移流方程式を数値計算した結果例を示します。このように差分化手法によって若干の特徴差が確認できますが、あるスカラー量\(q\)を輸送する方程式を記述しているということを覚えておきましょう。
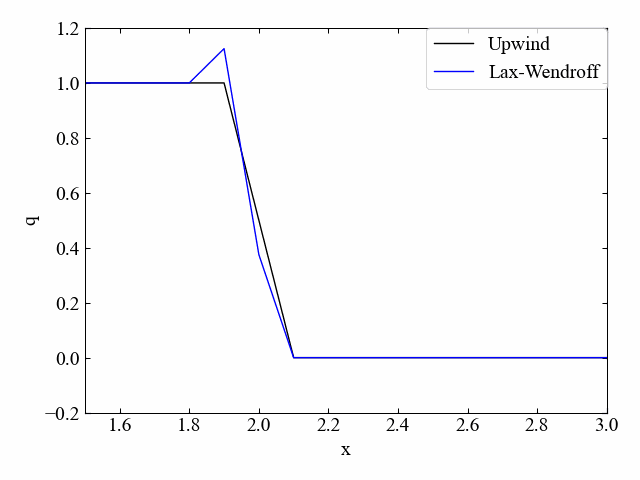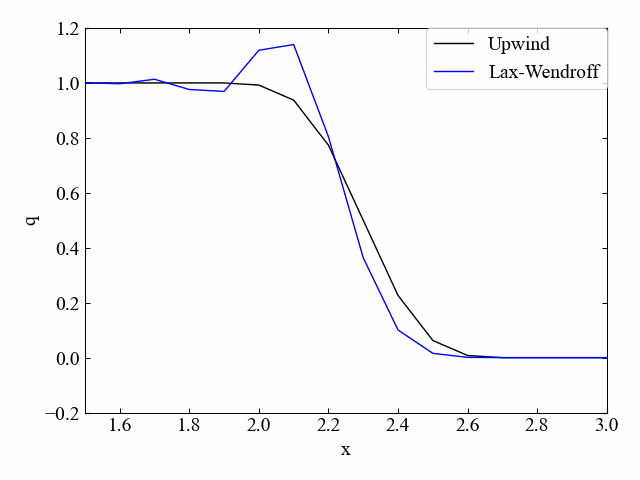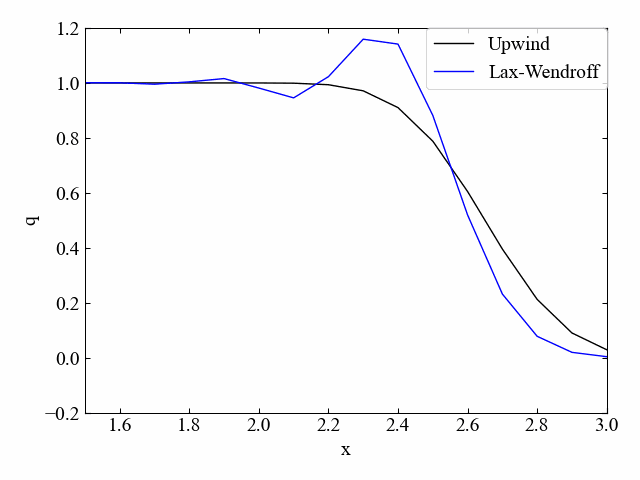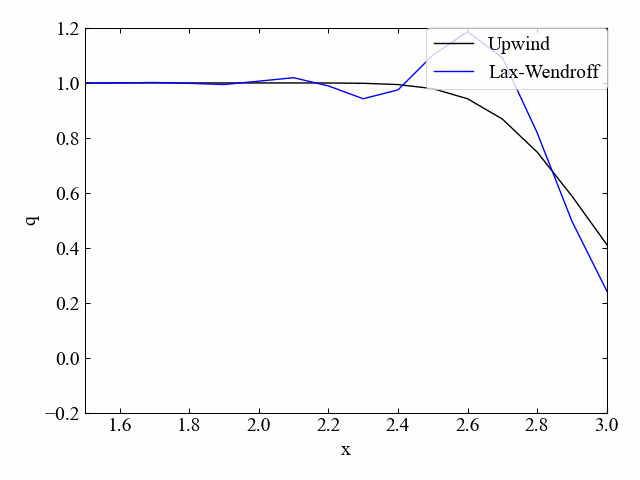
この記事で学ぶこと
この記事では、1次元で習得した差分方程式の作り方を2次元へ拡張します。差分化手法自体は1次元と特に違いがありませんが、2次元化するに当たってプログラミング部分に躓きポイントがあります。
当ブログでは過去に「Pythonで2次元ラプラス方程式を数値計算する方法」で2次元のコードを書きましたが、ここでは時間項がありませんでした。この記事では時間項を含む偏微分方程式の差分解法についてプログラミングしながら解説します。
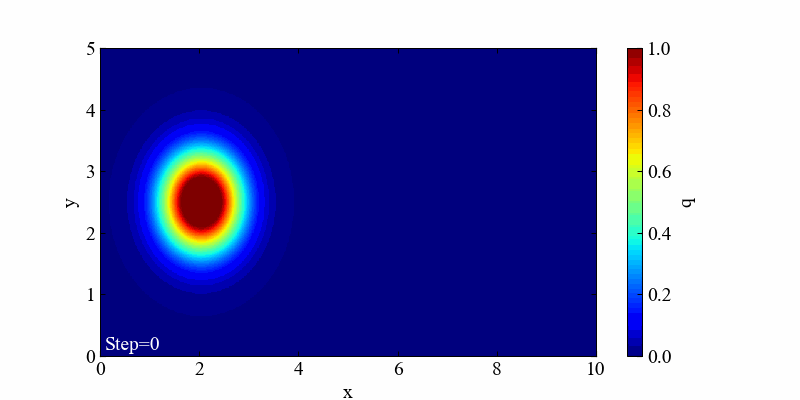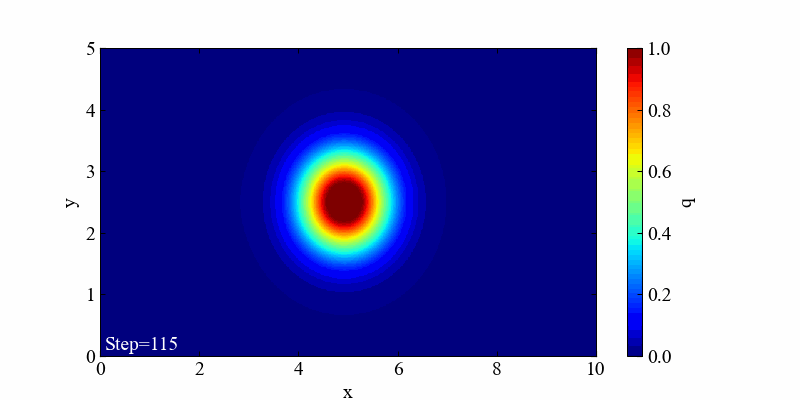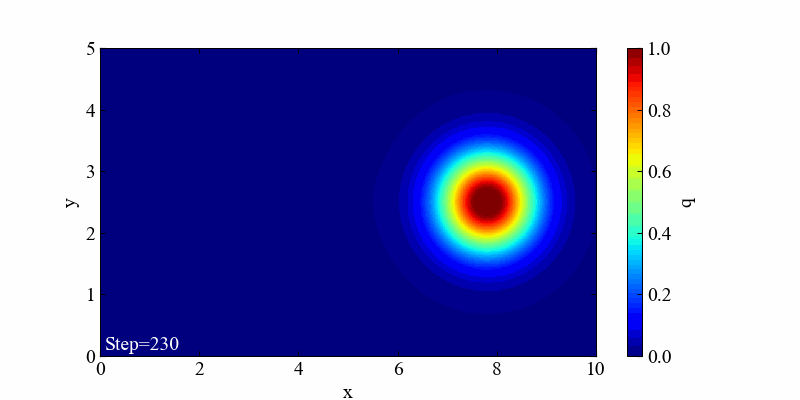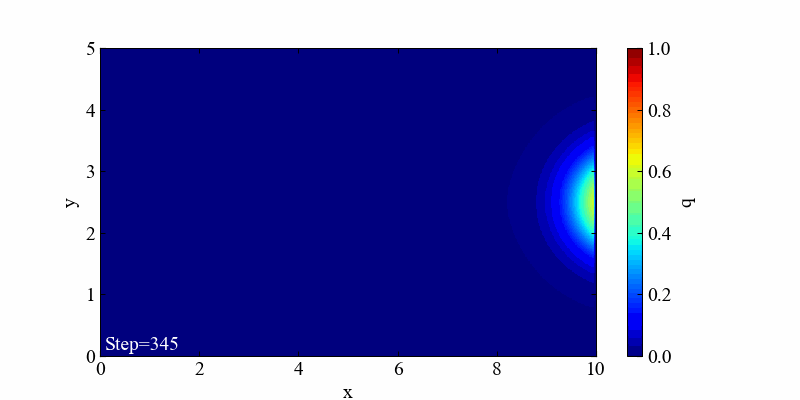
記事を最後まで読み進めることで、以下の動画を作る方法を学ぶことができます。この結果は2次元のガウス関数(確率密度関数)が単純に流れていくという結果です。
Pythonで2次元移流方程式の数値計算を実装するコード例
最後にコピペで動作する全コードを紹介しますが、コードを理解するために順を追って図や式を使いながら全体の説明をします。
動作環境
このページでは以下の環境で動作確認を行ったコードを掲載しています。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
| pillow | 7.1.2 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
計算格子
コンピュータは偏微分方程式を連続的な場で正確に解くことができません。そのため計算領域(空間)を離散化する必要があります。ここでは以下のような等ピッチ格子を計算領域として用意します。
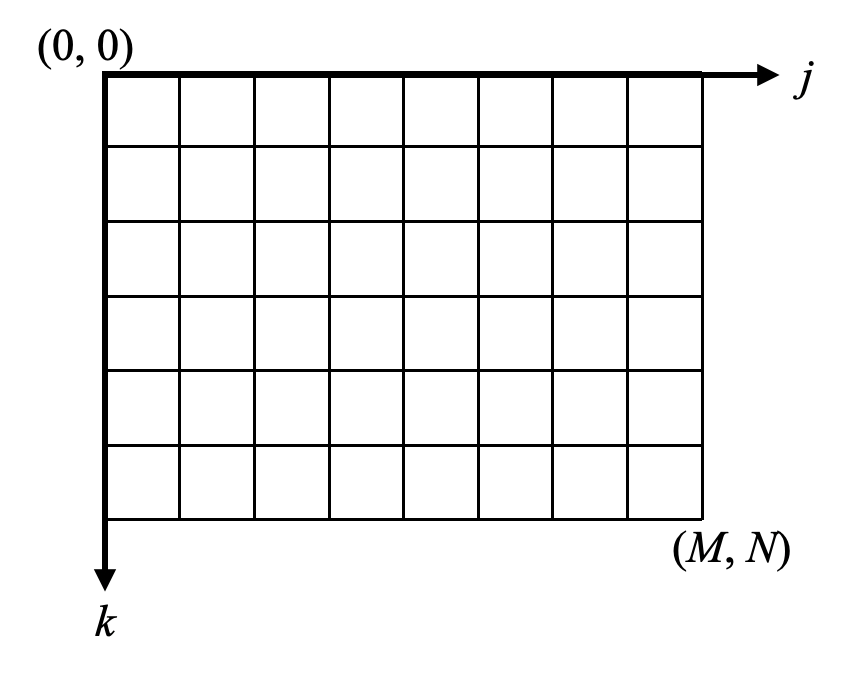
計算格子はinitial_field関数を用意して作成します。Webの記事ではnp.meshgridを使う方が多数だったので、ちょっと違う趣向ということで画像ライクな配列をnp.zerosで作成するようにしてみました。
ただし、その場合は行列の方向に注意が必要です。今回はx方向の方がy方向より長い管路をイメージした例を紹介しますが、np.zerosの入力順番に気を付ける必要があります。
|
1 2 3 4 5 6 7 8 9 |
def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場(x方向をj, y方向をkとする行列を作成→2D画像のデータ構造を模擬) x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(y), len(x))) return x, y, z |
こうすることで横方向に長い行列を作ることができます。これはそのまま表示させれば画像として結果を確認することができます。
|
1 2 3 4 5 6 7 8 9 10 |
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]] |
初期場
初期場も2次元空間に合わせて作ります。今回は2次元のガウス関数を使いましょう。ガウス関数は確率密度関数として正規分布を表現する時に使います。1次元の式は有名ですが、多次元ガウス関数の場合は式(2)となります。
ここで\(\Sigma\)は分散を\(n\)次元に一般化した分散共分散行列、\(\mathbf{\mu}\)は平均を\(n\)次元に一般化した平均ベクトルです。
これらの行列計算を得意とするNumPyで書いてみると容易に理解が進むと考えられます。式(2)を2次元の場合にどう記述するかを以下のコードに示します(initial_field関数に追記してみます。)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場(x方向をj, y方向をkとする行列を作成→2D画像のデータ構造を模擬) x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(y), len(x))) # 2D Gaussian(sigma:分散共分散行列, mu:平均ベクトル) sigma11 = 0.3 sigma22 = 0.3 sigma12 = 0 sigma21 = 0 mu_x = 2 mu_y = 2.5 sigma = np.array([[sigma11, sigma12], [sigma21, sigma22]]) mu = np.array([mu_x, mu_y]) det_sigma = np.linalg.det(sigma) inv_sigma = np.linalg.inv(sigma) # 式のj,kの順番と同じにするため転置させて計算する z = z.T for j in range(len(z)): for k in range(len(z.T)): X = np.array([x[j], y[k]]) z[j, k] = (1 / np.sqrt(2 * np.pi * det_sigma)) * np.exp((-1 / 2) * (X - mu).T @ inv_sigma @ (X - mu)) z = z.T return x, y, z |
forループ内の値を取りだす順番をx, yの順で行うためにループ端において転置しています。このコードで下図の初期場を得ます。
※xyの原点は左下ですが、格子の計算は左上から始めています。この辺は統一した方がよいかも??
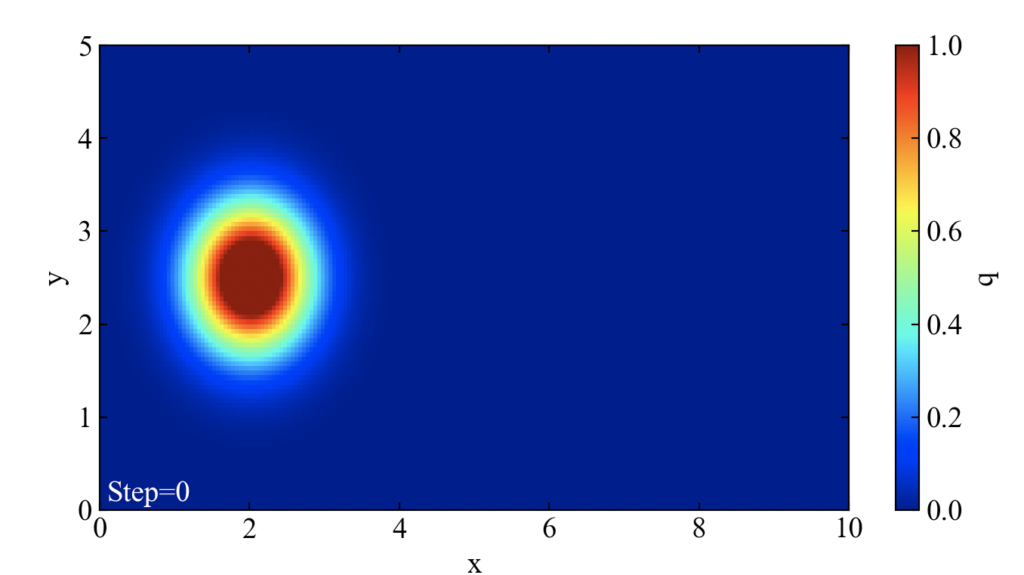
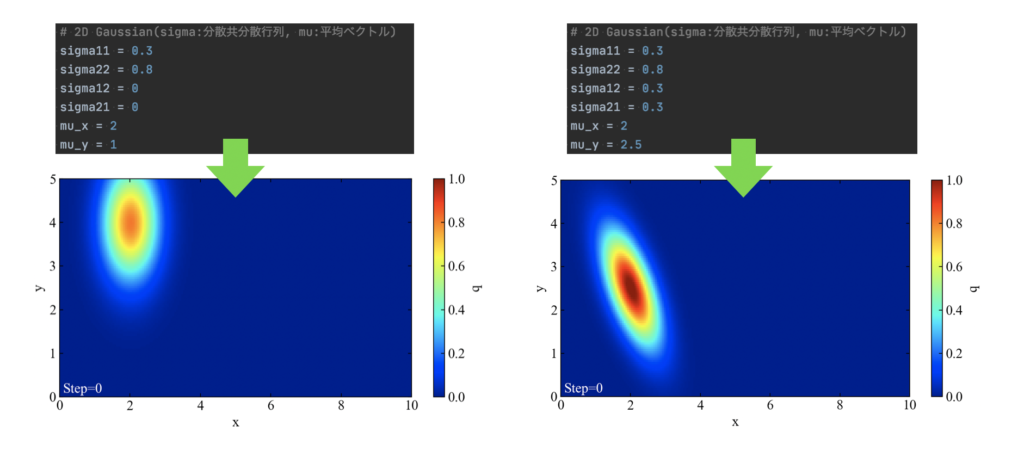
このように式で初期場を設定できるようにしておけば、下図のようにガウス関数の最大値位置(平均ベクトル)、アスペクト比(分散(分散共分散行列の対角項))、斜め具合(共分散(分散共分散行列の非対角項))を変化させることができます。
ソルバー(基礎方程式と離散化)
移流方程式の基礎方程式は式(3)です。\(\nabla\)は勾配を意味しており、式(3)を2次元空間で考えると式(4)と書くことができます\(^{[1]}\)。速度は各方向で異なる数値をとれるよう\(c\), \(d\)としています。
式(4)について、時間項を前進差分、空間項を風上差分で離散化すると式(5)を得ます。離散化の方法についての詳細は「Pythonで1次元移流方程式を離散化して数値流体力学に入門する」の方に記載していますので、まずは1次元で慣れておきましょう。
以下がコードです。forループは遅いのであまり使いたくないのですが、スライスや内積を使った記法を考えるのが面倒学習として理解するためにPythonを選択しているコンセプトと同様に、プログラム内計算順序がわかりやすいためforで書きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def sol_2d_advection(x, y, q, dt, dx, dy, c, d, step, dir, result_interval): ''' 輸送速度が正の2次元移流方程式を数値計算する ''' # 漸化式を反復計算 q = q.T for i in range(step): q0 = q.copy() for j in range(1, len(q) - 1): for k in range(1, len(q.T) - 1): q[j, k] = q0[j, k] - (c * (dt / dx)) * (q0[j, k] - q0[j-1, k]) - \ (d * (dt / dy)) * (q0[j, k] - q0[j, k-1]) # 指定した間隔で画像保存 if i % result_interval == 0: print('Iteration=', i) q = q.T plot(x, y, q, i, dir, 1) q = q.T return |
この関数は計算を担うソルバーと呼ばれる部分です。計算に必要な情報(格子、初期場や分解能、最終ステップ、保存先のアドレス…)を渡して計算します。
ポスト処理
格子準備や初期場の設定といった計算の準備を行うことをプリ作業と呼びますが、計算結果を確認する処理をポスト処理と呼びます(これらを行うソフトをプリポストソフトウェアとも呼ぶ)。
今回はプロットしてユーザーが目で確認できるようにする部分を以下のコードで作りました。matplotlibで可視化していますが、初期場の確認時には保存フラグsave_flagを0にして画像保存しないようにしたり、細かいことを色々やっています。
2D解析といえばコンター図で変化を確認するイメージだったので、書籍に載っているような3次元プロットではなくimshowを選択してみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
def plot(x, y, z, i, dir, save_flag): ''' 関数をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意して上下左右に目盛線を付ける。 x_size = 8 y_size = int(1 * x_size * (np.max(y) / np.max(x))) fig = plt.figure(figsize=(x_size, y_size)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 im = ax1.imshow(z, vmin=0, vmax=1, extent=[np.min(x), np.max(x), np.min(y), np.max(y)], aspect='auto', cmap='jet') ax1.text(0.1, 0.1, 'Step='+str(i), color="white") # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('q') # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) if save_flag == 1: # 画像を保存する plt.savefig(path) else: # グラフを表示する。 plt.show() plt.close() |
ただ、ここは完全に好みなので特に覚える必要はないと思います。
全コード(コピペ動作用)
以下に全コードを示します。dirで指定したディレクトリにresult_intervalの間隔で結果画像を保存していき、最後にcreate_gifでfilenameの動画を作ります。新しく条件を変更して動画を作成する時はdirの中身を削除しておく必要があります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 |
import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場(x方向をj, y方向をkとする行列を作成→2D画像のデータ構造を模擬) x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(y), len(x))) # 2D Gaussian(sigma:分散共分散行列, mu:平均ベクトル) sigma11 = 0.3 sigma22 = 0.3 sigma12 = 0 sigma21 = 0 mu_x = 2 mu_y = 2.5 sigma = np.array([[sigma11, sigma12], [sigma21, sigma22]]) mu = np.array([mu_x, mu_y]) det_sigma = np.linalg.det(sigma) inv_sigma = np.linalg.inv(sigma) # 式のj,kの順番と同じにするため転置させて計算する z = z.T for j in range(len(z)): for k in range(len(z.T)): X = np.array([x[j], y[k]]) z[j, k] = (1 / np.sqrt(2 * np.pi * det_sigma)) * np.exp((-1 / 2) * (X - mu).T @ inv_sigma @ (X - mu)) z = z.T return x, y, z def sol_2d_advection(x, y, q, dt, dx, dy, c, d, step, dir, result_interval): ''' 輸送速度が正の2次元移流方程式を数値計算する ''' # 漸化式を反復計算 q = q.T for i in range(step): q0 = q.copy() for j in range(1, len(q) - 1): for k in range(1, len(q.T) - 1): q[j, k] = q0[j, k] - (c * (dt / dx)) * (q0[j, k] - q0[j-1, k]) - \ (d * (dt / dy)) * (q0[j, k] - q0[j, k-1]) # 指定した間隔で画像保存 if i % result_interval == 0: print('Iteration=', i) q = q.T plot(x, y, q, i, dir, 1) q = q.T return def plot(x, y, z, i, dir, save_flag): ''' 関数をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意して上下左右に目盛線を付ける。 x_size = 8 y_size = int(1 * x_size * (np.max(y) / np.max(x))) fig = plt.figure(figsize=(x_size, y_size)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 im = ax1.imshow(z, vmin=0, vmax=1, extent=[np.min(x), np.max(x), np.min(y), np.max(y)], aspect='auto', cmap='jet') ax1.text(0.1, 0.1, 'Step='+str(i), color="white") # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('q') # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) if save_flag == 1: # 画像を保存する plt.savefig(path) else: # グラフを表示する。 plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) imgs = [] # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=50, loop=0) return if __name__ == '__main__': ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する ''' # 画像保存フォルダと動画ファイル名 dir = 'img_2d_advection' filename = '2d-advection.gif' # 時間項の条件 dt = 0.025 # 空間項の条件 dx = 0.05 dy = 0.05 x_max = 10 y_max = 5 # 初期場を用意する x, y, q = initial_field(x_max, y_max, dx, dy) plot(x, y, q, 0, dir, 0) # 輸送速度c, d c = 1 d = 0 # クーラン数の確認 nu_x = c * dt / dx nu_y = d * dt / dy print('Courant number=', nu_x, nu_y) # 計算を実行 sol_2d_advection(x, y, q, dt, dx, dy, c, d, 350, dir, 5) # GIF動画を作成 create_gif(dir, filename) |
実行結果①:横方向に動かしてみる
このコードをそのまま実行すると、冒頭で紹介した以下の動画が出力されます。
空間分解能dx, dyや時間分解能、結果保存間隔によってアニメーションの見かけの速度が変化します。
移流方程式の厳密解は分布の形を変えない移動現象でしたが、計算が進むにつれて最大値がやや小さくなっていく結果を得ました。これは1次元の記事でも確認した通り、クーラン数が1よりも小さい時に起こる数値拡散(数値減衰)です。

アニメーションの速度を変更したい場合はcreate_gif内のduration値を変更します(大きい値で遅くなる)。
実行結果②:斜めに動かしてみる
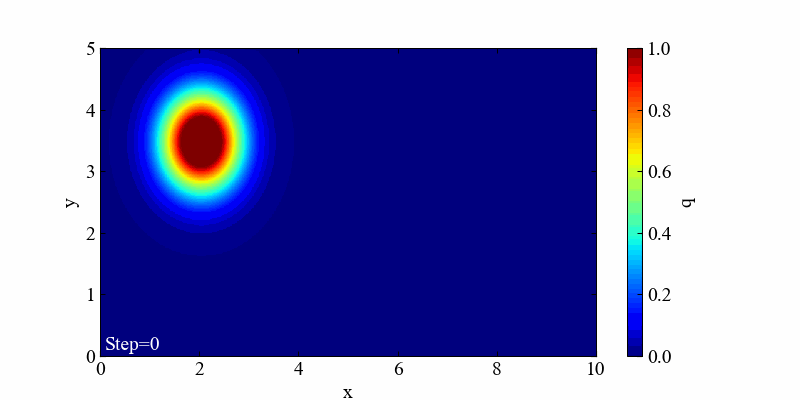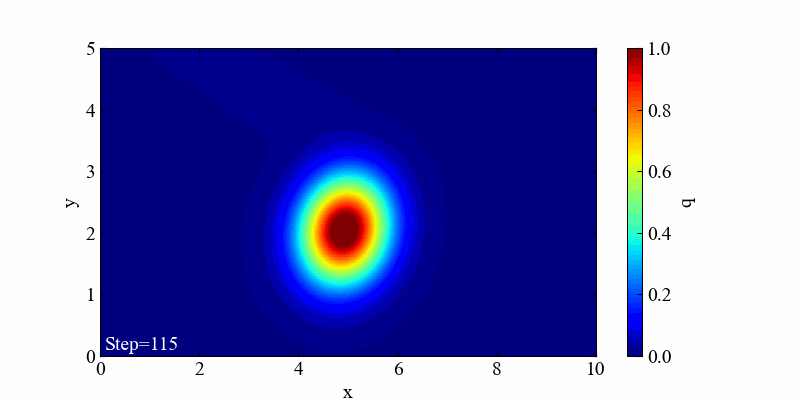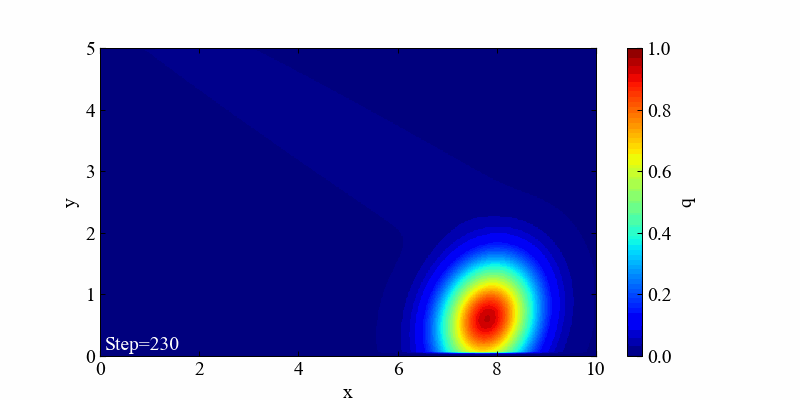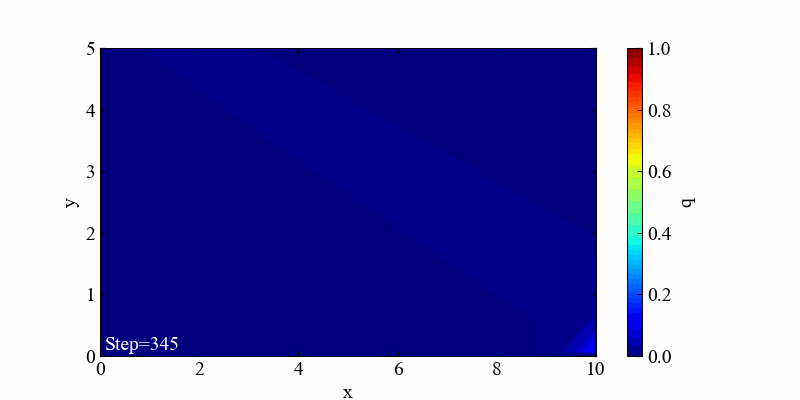
平均ベクトルのy成分mu_yを1.5、y方向速度dを0.5として斜めに動かしてみます。
出だしのガウス分布が少し境界からはみ出ていたので、上の方に値を引きずっているような挙動がありますが、これも移流の特徴と思います。きっちり分布の移動を表現したい場合は境界を十分遠ざけた方が良さそうです。
実行結果③:発散例
風上差分だけど逆走してみる
最後はお約束の発散動画でオチとしましょう。まずはこちら。
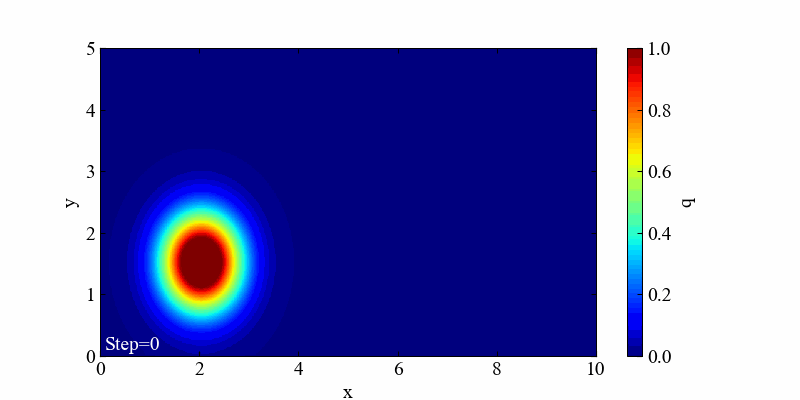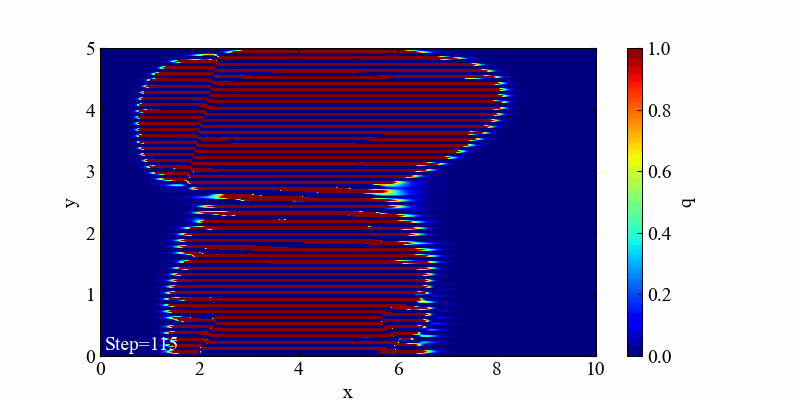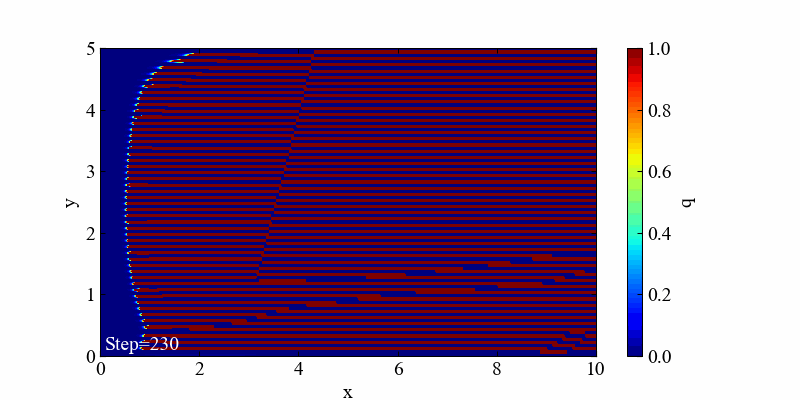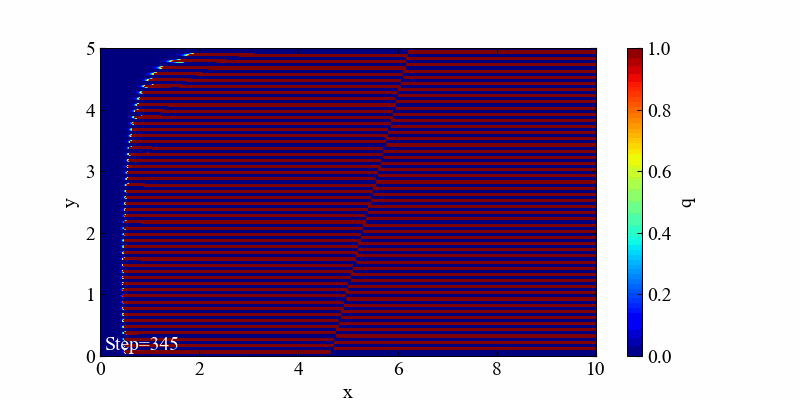
この発散は空間項を風上差分で離散化しているところを、d=-0.5とあえて逆走させた場合の発散例です。風上として後ろの情報を使って解く手法なのに、風下の情報を使ってしまったことによって空間の値が崩壊しました。
これを防ぐ方法は式の中で場合分けするか、Lax法やLax-Wendroff法のような安定した中心差分系の空間離散化手法を選択する必要があります。
クーラン数を1以上にしてみる
続いてこちら。さらに爆発感が出ていますね。
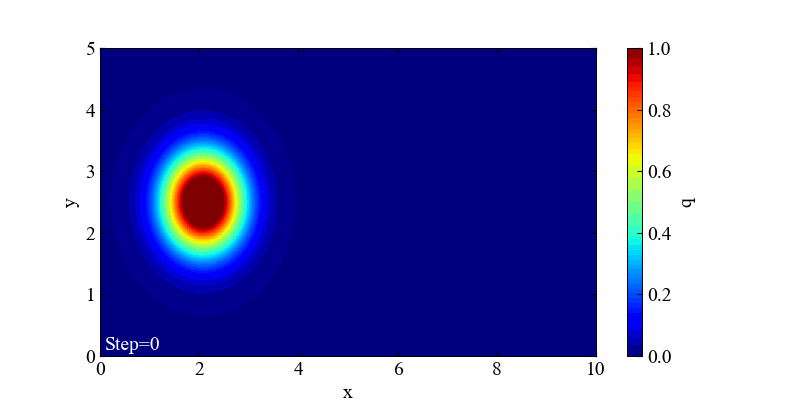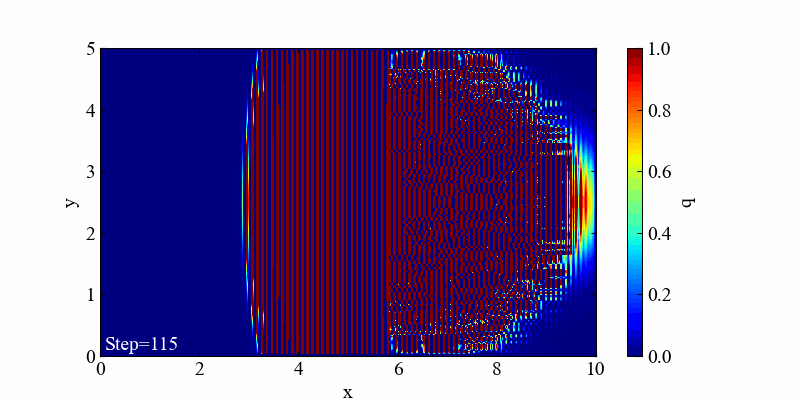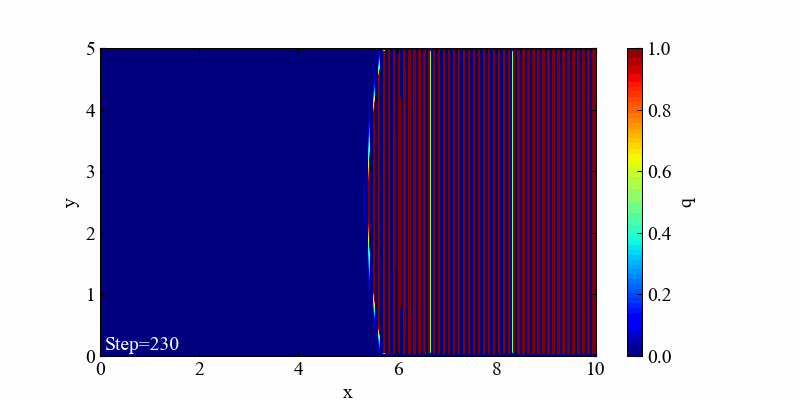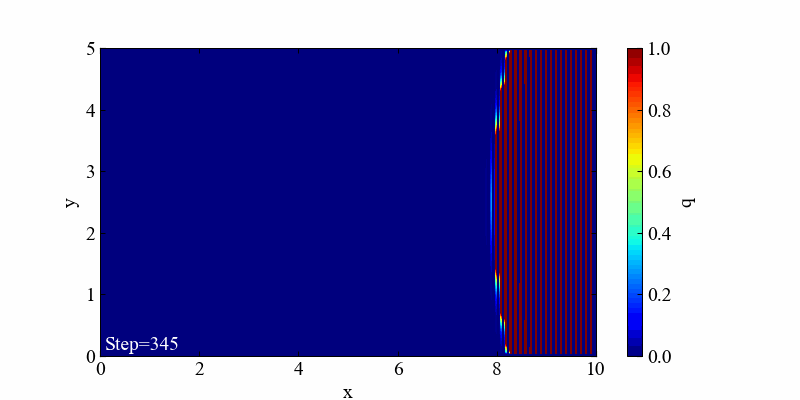
この発散はクーラン数を1以上(c=2.5)にしてみた結果です。時間と空間の分解能によって決まる制限速度を超えてしまうと容易に発散します。これを防ぐには時間と空間の分解能、そして速度の関係を適切に設定するしかありません。
発散間際にガウス分布が進行方向に対して潰れ、楕円形状になっていました。光速に近づく時に問題となるローレンツ収縮みたいで面白いですね。
まとめ
このページでは1次元移流方程式のおさらいから始め、2次元移流方程式の概要を紹介しました。
Pythonによるコーディングと式の関係を対応させながら説明し、最後はアニメーションで結果を確認し理解を深めました。
初期場として多次元のガウス関数を使いましたが、数値流体解析分野ではGaussian Hill問題として多用されているようです。
計算は成功例だけでなく発散例も示していますので、もし計算がうまくいかない時は条件の見直しを考えてみてください。
Pythonでforループを使いながら数値計算するのは計算速度の観点からあまりされないことと思いますが、特にプログラミングに関する知識が十分なくても式をそのまま記述できるため、学習としては最適だと感じました。
速度が求められる場面ではC++やFortranが良いかも?NumPyのスライスや内積記法、Cythonの使用はどうだろう?…と色々手段はありそうです(ピュアPythonもバージョンアップで日々速度UPされるそうですし)。
とりあえず2次元の移流方程式までは理解できたと思います(多分)\((\nu \cdot \nabla)\nu\)
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!