最小二乗法は実験データに曲線をフィットさせる有効な手段です。直線や多項式が有名ですが、円状に分布したデータにカーブフィットさせたい時もあるでしょう。今回は最小二乗法を円の方程式に対して適用してカーブフィットするPythonコードを紹介します。
こんにちは。wat(@watlablog)です。ここでは円状のデータにカーブフィットさせるPythonコードを書いてみます！
円の方程式に最小二乗法を適用する方法
円の方程式
最小二乗法は「Pythonでカーブフィット！最小二乗法で直線近似する方法」という記事で直線近似を紹介しました。円の場合でもこの手続きは同様です。元の方程式によって最終的に解く連立方程式の形が変わるだけです。
上記記事では愚直に式展開を行って、若干回りくどい方法を取っていましたが。今回は少し線形代数の小技を使ってみます。
今回対象とするデータは下図のような円状データです。このような分布を持つデータは直線や多項式で近似する事ができません。
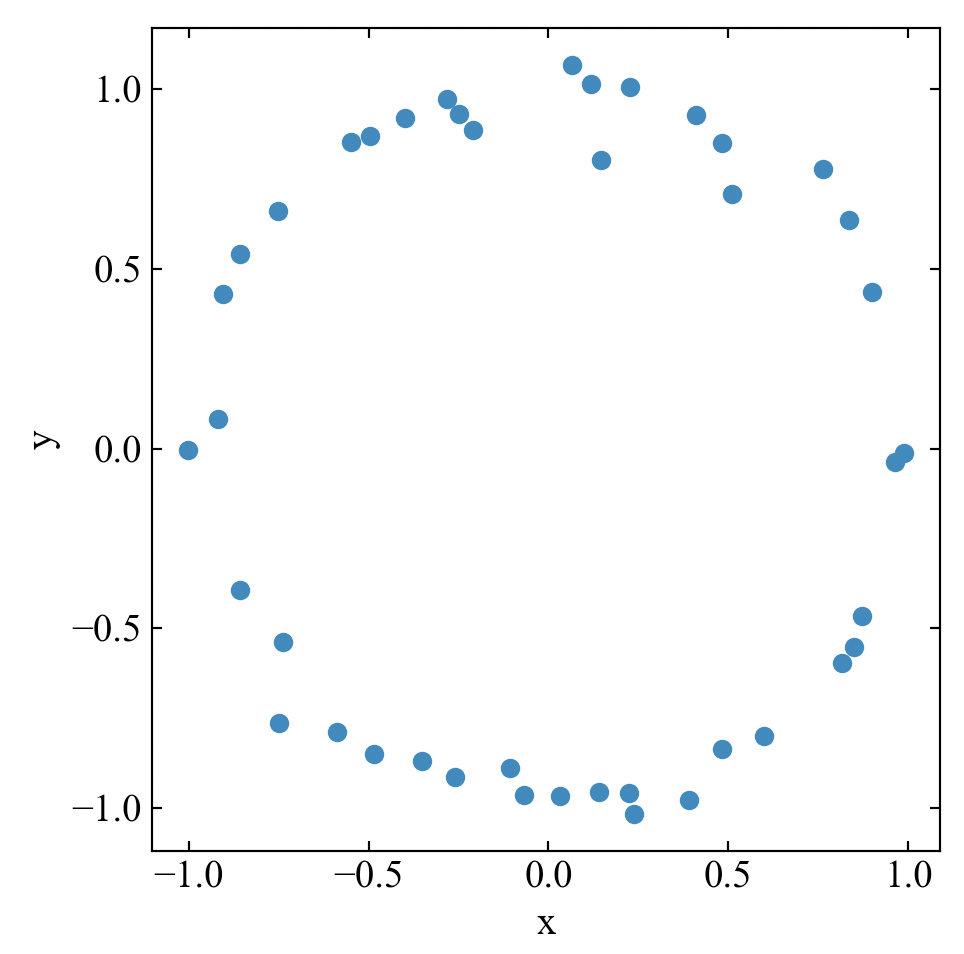
円状のデータなので円の方程式に対してフィットさせる事を考えます。円の方程式は式(1)で示す通り、\(x\)軸と\(y\)軸上のずれ\(a\), \(b\)と半径\(r\)で表現する事ができます。
\[
(x-a)^{2} + (y-b)^{2} = r^{2}
\tag{1}
\]
各パラメータを図示したものが下図。この記事では先ほどのデータにうまくフィットする円の方程式を求める事を行います。
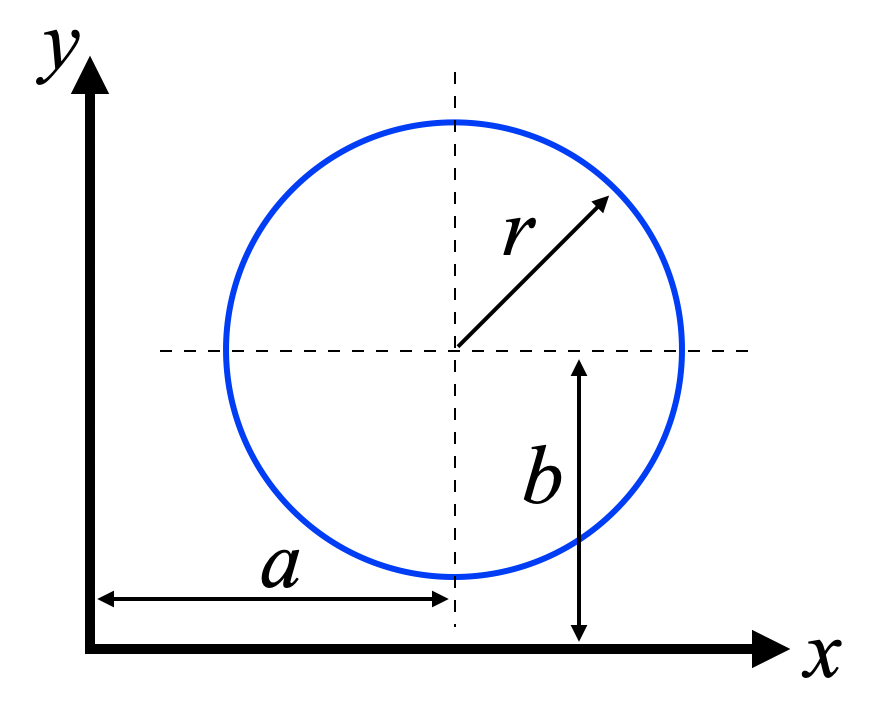
最小値を求める式の導出
式(1)の円の方程式を式(2)と変形し、距離の二乗との差分を求める形にします。
\[
(x-a)^{2} + (y-b)^{2} - r^{2} = 0
\tag{2}
\]
変数\(x\)と\(y\)を、データ点毎に入力できるような\(x_{i}\)、\(y_{i}\)に変換、二乗誤差を求める事ができるように式(3)と関数\(S\)を作ります。ここでは見やすさのために総和記号の範囲指定を省略しています（範囲はデータ数全部です）。
\[
S=\sum \{(x_{i}-a)^{2} + (y_{i}-b)^{2} - r^{2}\}^{2}
\tag{3}
\]
最小値問題は微分を行いますが、式(3)はまだ微分し難いので大括弧の中身を式(4)と展開します。
\[
S=\sum (x_{i}^{2} - 2ax_{i} + a^{2} + y_{i}^{2} - 2b y_{i} + b^{2} - r^{2})^{2}
\tag{4}
\]
最小二乗法では未知変数の偏微分を行いますが、式(4)には未知変数の二乗項があるので、以下のように変数をまとめるテクニックを使います。
\[
\left\{\begin{eqnarray}
A&=&-2a\\
B&=&-2b\\
C&=&a^{2} + b^{2} - r^{2}
\end{eqnarray}\right.
\]
式(4)をまとめた変数で書き換えると式(5)となります。
\[
S=\sum (x_{i}^{2}+y_{i}^{2}＋Ax_{i}+By_{i}+C)^{2}
\tag{5}
\]
式(5)を\(A, B, C\)でそれぞれ偏微分し、\(=0\)とする事で最小値問題を解く式(6)を得ます。この連立方程式を解けば未知変数（円のパラメータ）を得ます。
\[
\left\{
\begin{eqnarray}
\frac{\partial S}{\partial A}&=&\sum 2(x_{i}^{3}+x_{i}y_{i}^{2}＋Ax_{i}^{2}+Bx_{i}y_{i}+Cx_{i})=0\\
\frac{\partial S}{\partial B}&=&\sum 2(x_{i}^{2}y_{i}+y_{i}^{3}＋Ax_{i}y_{i}+By_{i}^{2}+Cy_{i})=0\\
\frac{\partial S}{\partial C}&=&\sum 2(x_{i}^{2}+y_{i}^{2}＋Ax_{i}+By_{i}+C)=0\\
\end{eqnarray}
\right.
\tag{6}
\]
連立方程式を解き円のパラメータを得る
式(6)は3元連立1次方程式なので、左辺に未知変数\(A, B, C\)の項、右辺にそれ以外の項を配置させた式(7)と変形した方が行列として扱えるので簡単です（2は全ての方程式に入っているので同値変形として消しています）。
\[
\left\{
\begin{eqnarray}
\frac{\partial S}{\partial A}&=&\sum(Ax_{i}^{2}+Bx_{i}y_{i}+Cx_{i})=-\sum(x_{i}^{3}+x_{i}y_{i}^{2}）\\
\frac{\partial S}{\partial B}&=&\sum(Ax_{i}y_{i}+By_{i}^{2}+Cy_{i})=-\sum(x_{i}^{2}y_{i}+y_{i}^{3})\\
\frac{\partial S}{\partial C}&=&\sum(Ax_{i}+By_{i}+C)=-\sum(x_{i}^{2}+y_{i}^{2})\\
\end{eqnarray}
\right.
\tag{7}
\]
行列形式にすると式(8)となります。左辺の係数行列を見ると規則性を持っていて面白いですね。
\[
\begin{bmatrix}
\sum x_{i}^{2}& \sum x_{i}y_{i} &\sum x_{i} \\
\sum x_{i}y_{i}& \sum y_{i}^{2} & \sum y_{i} \\
\sum x_{i} & \sum y_{i} & \sum 1
\end{bmatrix}
\begin{Bmatrix}
A\\
B\\
C
\end{Bmatrix}
=
\begin{bmatrix}
-\sum (x_{i}^{3} + x_{i}y_{i}^{2})\\
-\sum (x_{i}^{2}y_{i} + y_{i}^{3})\\
-\sum (x_{i}^{2} + y_{i}^{2})
\end{bmatrix}
\tag{8}
\]
式を書くのが大変なので見やすくするために式(8)を式(9)と書き換えます。
\[
[M]\{X\}=[Y]
\tag{9}
\]
式(9)は式(10)と逆行列を使う事で未知数ベクトル\(\{X\}\)を求める事が可能です。
\[
\{X\}=[M]^{-1}[Y]
\tag{10}
\]
Pythonで逆行列を求めるのは簡単ですが、余因子を使う事で手計算で逆行列を求める事が可能です（3×3の計算すらやりたくないですが）。逆行列についての解説は「Python/NumPyで線形代数！linalgで逆行列を求める方法」という記事に記載していますので、是非ご覧ください。
後は式(5)の手前でまとめる前の変数で式(11)と計算する事で、求めたかった円のパラメータ\(a, b, r\)を得る事ができます。
\[
\left\{\begin{eqnarray}
a &=& -\frac{A}{2}\\
b &=& -\frac{B}{2}\\
r &=& \sqrt{a^{2} + b^{2} - C}
\end{eqnarray}\right.
\tag{11}
\]
以上で式解説編は終了です。ここからはPythonで計算するコードを書いてみましょう。
最小二乗法で円をカーブフィットするPythonコード例
動作環境
PC
| Windows |
OS |
Windows10 64bit |
| CPU |
Intel 11th Core i7-11800H:2.3[GHz] |
| メモリ |
16[GB] |
| Mac |
OS |
macOS Catalina 10.15.7 |
| CPU |
1.4[GHz] |
| メモリ |
8[GB] |
Python環境
| Python |
Python 3.9.6 |
| PyCharm (IDE) |
PyCharm CE 2020.1 |
| Numpy |
1.21.1 |
| matplotlib |
3.4.3 |
カーブフィット関数
以下のコードが今回作った円の方程式でカーブフィットする関数です。Pythonだと式のイメージそのままだと思いますので、特にコードの解説は不要でしょう。
この関数はデータセットとして\(x_{i}, y_{i}\)（それぞれ配列）を受け取り、戻り値として円のパラメータを返します。
|
|
# 円の方程式でカーブフィットする関数 def circle_fitting(xi, yi): M = np.array([[np.sum(xi ** 2), np.sum(xi * yi), np.sum(xi)], [np.sum(xi * yi), np.sum(yi ** 2), np.sum(yi)], [np.sum(xi), np.sum(yi), 1*len(xi)]]) Y = np.array([[-np.sum(xi ** 3 + xi * yi ** 2)], [-np.sum(xi ** 2 * yi + yi ** 3)], [-np.sum(xi ** 2 + yi ** 2)]]) M_inv = np.linalg.inv(M) X = np.dot(M_inv, Y) a = - X[0] / 2 b = - X[1] / 2 r = np.sqrt((a ** 2) + (b ** 2) - X[2]) return a, b, r |
全コード（プロットして確認）
matplotlibでプロットする所まで含めた全コードを紹介します。ここでは原点(0, 0), 半径1の円にノイズを含ませた点をデータとしています。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
import numpy as np from matplotlib import pyplot as plt, patches # サンプル円データを生成 def generate_circle_points(a, b, r, dx): # 原点(0, 0)の円を用意 x = np.arange(-r, r, dx) yp = np.sqrt(r ** 2 - x ** 2) ym = -yp xi = np.concatenate([x, x]) yi = np.concatenate([yp, ym]) # a, bでオフセットする xi += a yi += b return xi, yi # 円の方程式でカーブフィットする関数 def circle_fitting(xi, yi): M = np.array([[np.sum(xi ** 2), np.sum(xi * yi), np.sum(xi)], [np.sum(xi * yi), np.sum(yi ** 2), np.sum(yi)], [np.sum(xi), np.sum(yi), 1*len(xi)]]) Y = np.array([[-np.sum(xi ** 3 + xi * yi ** 2)], [-np.sum(xi ** 2 * yi + yi ** 3)], [-np.sum(xi ** 2 + yi ** 2)]]) M_inv = np.linalg.inv(M) X = np.dot(M_inv, Y) a = - X[0] / 2 b = - X[1] / 2 r = np.sqrt((a ** 2) + (b ** 2) - X[2]) return a, b, r # サンプルデータ作成 xi, yi = generate_circle_points(0, 0, 1, 0.1) noise = np.random.normal(loc=0, scale=0.05, size=len(xi)) xi += noise yi += noise # サンプルデータに対してカーブフィット a, b, r = circle_fitting(xi, yi) print('a=', a, 'b=', b, 'r=', r) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(5, 5)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットの準備。 ax1.scatter(xi, yi, label='dataset') circle = patches.Circle( (a, b), r, facecolor='None', linestyle='--', edgecolor="red", label="circle fitting") ax1.add_patch(circle) ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() |
以下が結果です。いい感じに円がフィットしています。
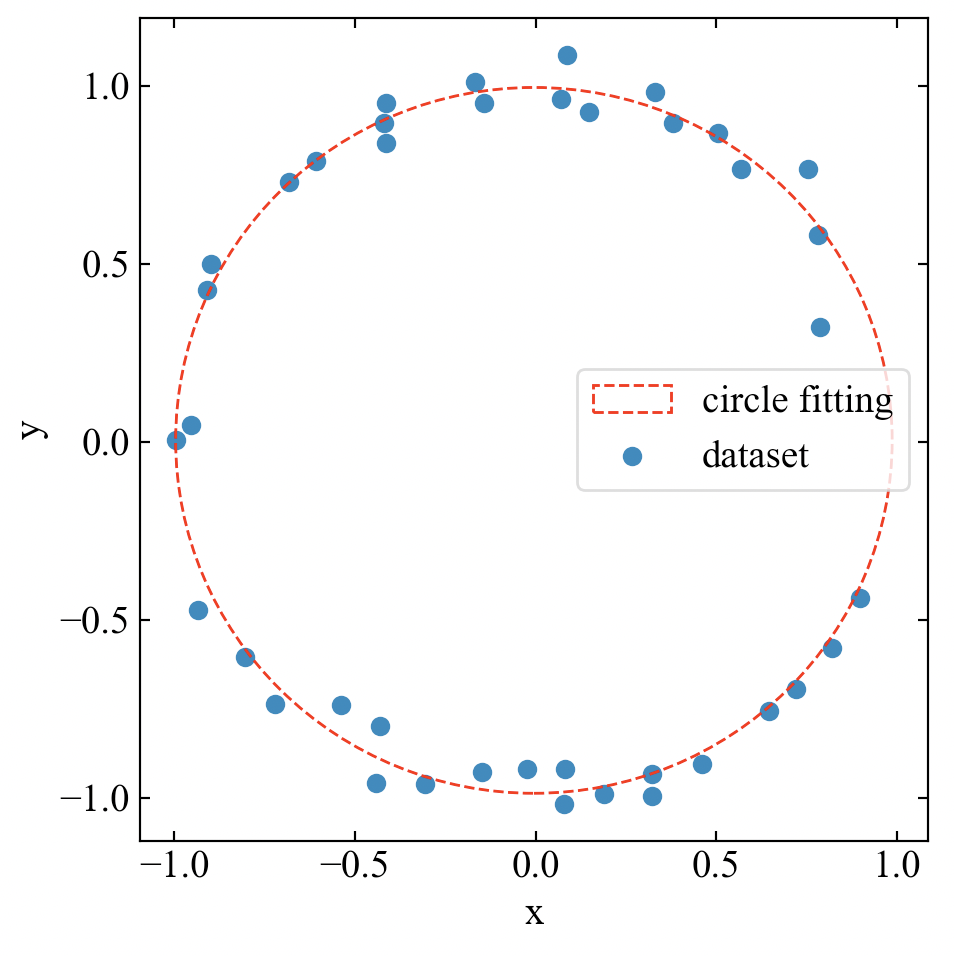
出力ウィンドウには円のパラメータがprintされます。データのばらつきにより誤差がありますが、指定した原点座標と半径になっているようです。
|
|
a= [-0.02283454] b= [-0.01599577] r= [1.01234544] |
ノイズ無しデータでテスト
本当に式合ってるの？という疑問もあると思うので、一度ノイズを含まないデータを使って確認してみましょう。
先ほどのコードでサンプルデータを作成している部分を以下のように変更します。データ点の数も少なくしてみましょう。
|
|
# サンプルデータ作成 xi, yi = generate_circle_points(0, 0, 1, 0.6) #noise = np.random.normal(loc=0, scale=0.05, size=len(xi)) #xi += noise #yi += noise |
以下が得られたプロットです。ぴったりと点にフィットしているので式は大丈夫でしょう（結果論）。
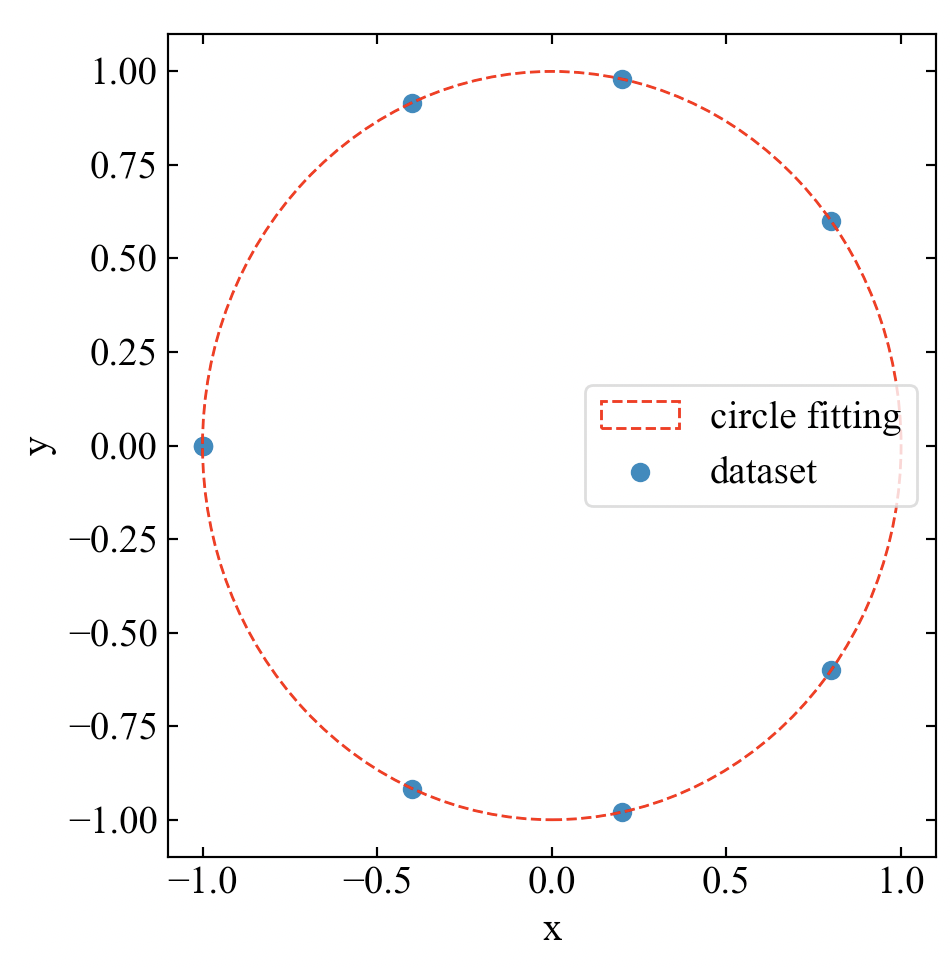
得られた円のパラメータは以下です。寸分の狂いもないので式は大丈夫でしょう（結果論）。
|
|
a= [-0.] b= [-0.] r= [1.] |
中心座標変更データでテスト
中心座標をずらしても機能するの？という事を確認します。方程式はオフセット円も考慮に入れているので、ちゃんとフィットするはず。
データ作成部分を以下に変更します。
|
|
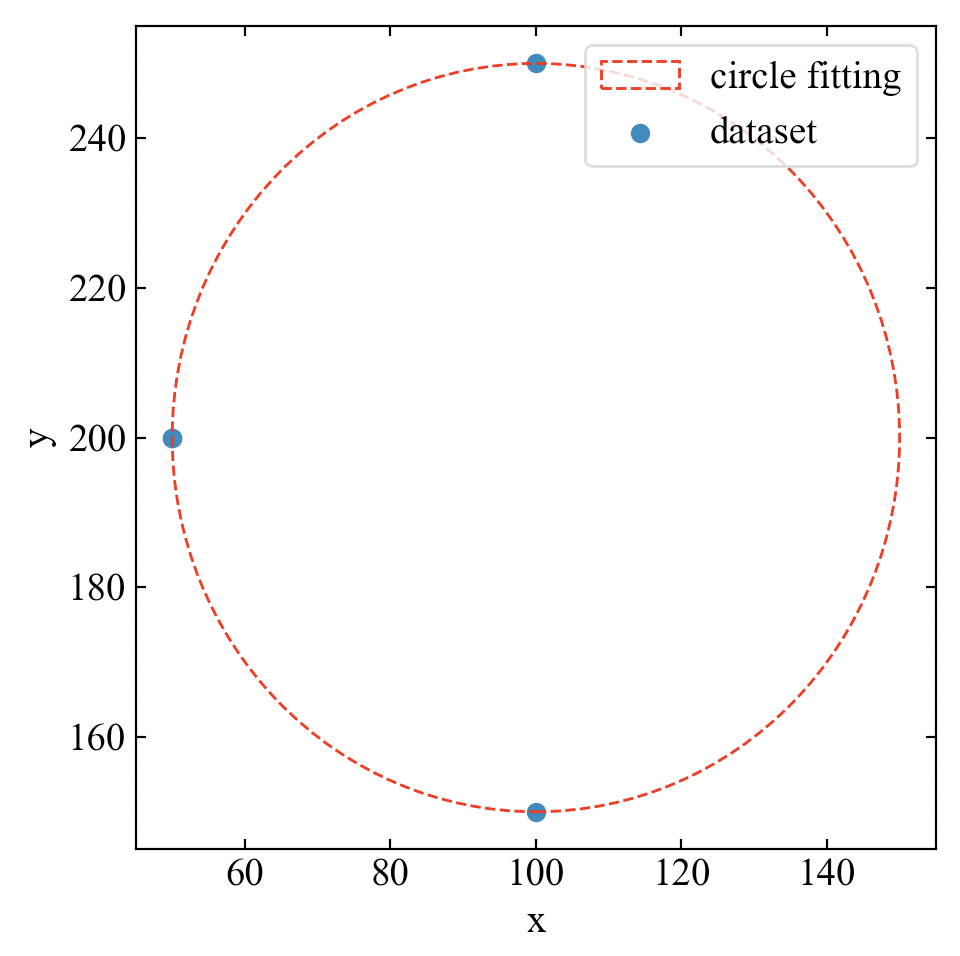
# サンプルデータ作成 xi, yi = generate_circle_points(100, 200, 50, 50) #noise = np.random.normal(loc=0, scale=0.05, size=len(xi)) #xi += noise #yi += noise |
下図のプロットを得ました。また出力値も指定した円のパラメータと一致したので、式は大丈夫そうです（結果論）。
|
|
a= [100.] b= [200.] r= [50.] |
まとめ
これまで直線や多項式へのカーブフィッティングを行ってきましたが、円へのフィット需要も一定数ありそうなのでやってみました。
直線から円になっても式展開や最小二乗の方法、手続きは全く同じなので、そんなに悩まず式を導出する事ができました。
求めた式を使ってノイズを含んだデータ点、ノイズ無しのデータ点で検証を行いました。
円のカーブフィットを行う事で、測定によって得られた幾何的な補正処理とかに役立ちそうです。
Python（というよりNumpy？）は行列演算が得意で数式をコード上にほぼそのまま記載する事ができます。ちょっと思い立ってプロットするだけならそんなに工数もかからないのでお勧めです。
カーブフィットシリーズに円を加える事ができました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
