
連立方程式を解いたりする時は行列形式のデータをよく扱います。その時に使う逆行列計算は手計算だと非常に面倒ですが、Pythonの線形代数モジュールであれば簡単に求めることが出来ます。
こんにちは。wat(@watlablog)です。
今回は小技として行列の逆行列をPythonで求める方法を紹介します!
逆行列の例
この記事の前半大部分は一般的な逆行列に関するメモを記載しています。
Pythonプログラムのみ見たい方は目次からコード部分までジャンプして下さい。
2×2行列の場合の逆行列の求め方
行列については高校数学で習う人が多いと思いますが、線形代数という分野で学びます。
逆行列とは、簡単に言うと行列の場合の逆数を意味します。
方程式で式変換をがちゃがちゃやっている時、例えば\(a\)という実数であれば\(1/a\)が逆数となり、\(a\)に\(1/a\)をかけると1になります。この特性を利用して式を簡単にしたり変形します。
行列には大きさがあり、式(1)のような2行、2列の行列は2×2行列と呼ばれます。
\[
[A]= \begin{pmatrix}
a & b\\
c & d
\end{pmatrix}\tag{1}
\]
この行列の逆行列は以下の式(2)で計算可能です。2×2の場合は覚えている方も多いのではないでしょうか。
\[
[A]^{-1}= \frac{1}{ad-bc}\begin{pmatrix}
d & -b\\
-c & a
\end{pmatrix}\tag{2}
\]
ここで、式(2)内の\(ad-bc\)は行列式とよばれるもので、数学的には\(\left | A \right |\)または\(\det[A]\)と書くこともあります。
逆行列を求める場合は、この\(\det[A]\)が0でないことが条件となります。
3×3行列以上の場合の逆行列の求め方
先ほどの式は2×2行列にしか適用できないのですが、実用上はどんな大きさの行列に対しても逆行列を求める必要があります。
3×3行列の場合でどのように解くか見てみましょう。
逆行列を求める定義式は式(2)を一般化して式(3)と表します。ここで、\(\det[A]\)は先ほど説明した行列式を意味し、0で無い事が制約条件です。また\(\tilde{[A]}\)は余因子行列と呼ばれ、行列\([A]\)の各成分で余因子を取ってから転置させた行列です。
少々計算量がありますが、3×3以上の行列式の求め方、余因子行列の求め方を説明してから逆行列を求めたいと思います!
実はこれから説明する方法を使うと2×2行列の逆行列の公式を導く事が出来ます。
余因子とは?
2×2行列の場合は有名な公式を使って行列式を求めましたが、3×3行列以上の場合は少々やっかいです。
サラスの公式という方法で求める事が可能ですが、計算量が減るわけでも無いのと、4×4以上の正方行列で使えないという事もあり、僕は余因子展開を使った求め方だけ知っていれば良いかなと思っています。
行列\([A]\)の\(i\)行目\(j\)列目の成分を\(a_{ij}\)とし、\(a_{11}\)成分の余因子を考えると、以下の図で示す事が可能です。
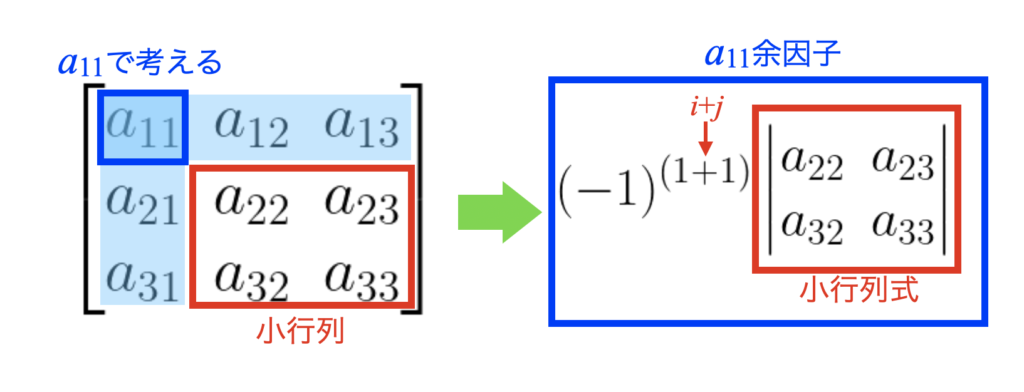
同様に、\(a_{22}\)の余因子は下図となります。

このように余因子\(A_{ij}\)とは、\(-1\)の\((i+j)\)乗に自成分以外の行列で作成した小行列式\(|M_{ij}|\)をかけたものであり、式(4)と定義されます。
この余因子を使う事で何×何行列の行列式も機械的に求める事が可能です(手計算はやっぱり大変ですが…)。
余因子展開で\(\det[A]\)を求める
正方行列\([A]\)の行列式\(\det [A]\)は余因子展開で求める事が可能です。
余因子展開による行列式の求め方は、式(4)の余因子を使って任意の行、列に対して行う操作です。行方向に行う場合は式(5)、列方向に行う場合は式(6)と表します。
第1行で展開する場合は式(5)で\(i=1\)と固定し、\(j\)を\(n\)まで増加させて加算させていくという展開の仕方をします。
言葉だとなかなか伝わらないため、例題を計算してみましょう。
ここでは以下の行列\([A]\)を例題とします。
この行列\([A]\)の行列式を式(7)と第2行で展開してみます。第何行、第何列で展開しても同じ答えとなる所が面白いです。
余因子行列を求める
余因子行列は式(8)で求める事が出来ます。すごく大変そうな式ですが、各\(ij\)成分毎に式(4)を考えているだけなので、作業的に作成可能です。
例題の行列\([A]\)に対して余因子行列を求めてみると、式(9)となります。転置記号がついている部分にご注意下さい。
余因子展開結果と余因子行列から逆行列を計算する
式(3)を再掲します。例題では式(7)の\(\det[A]\)と式(9)の\(\tilde{[A]}\)が求められましたので、逆行列\([A]^{-1}\)は式(10)と求める事が可能です。
この逆行列と元の行列の積をとる事で単位行列となります(計算が大変なのでこちらは下で説明するPythonコードで確かめました)。手計算やプログラムで逆行列を求めた場合、単位行列を使った検証を行うのはポカ避けとして非常に重要です。
3×3行列に対して余因子を考えると、小行列式の次元が1つ下がって2×2になるから公式が使えてまだ良いけど、4×4行列以上になってくると手計算では解きたくありませんね!
プログラムで計算する需要が高い理由がわかります…。
参考:一般化逆行列について
逆行列は主に連立方程式を解くために計算します。教科書に載っているような必ず解が存在する問題の場合は上記正方行列から計算される逆行列で十分です。
しかし、現実問題は様々な誤差を含み、計測されたデータから綺麗に解を求める事が困難な問題ばかりです。
そのような場合、方程式の係数行列\([A]\)は必ずしも正方行列になりません。
そういった問題に対応するために一般化逆行列(Generalized inverse)が使われます。一般化逆行列はムーア・ペンローズの擬似逆行列が有名で、擬似逆行列、擬逆行列、一般逆行列…と様々に呼ばれています。
一般化逆行列は\([A]^{+}\)と書き、
求めたい未知数の数より式の数が多い場合(\([A]\))が縦長長方形)は、式(11)で与えられます。
逆に求めたい未知数の数より式の数が少ない場合(\([A]\))が横長長方形)は、一般化逆行列は式(12)で与えられます。
一般化逆行列の具体的なイメージは方程式を実際に解いてみるのが良いと思います。事例についてはそのうち別記事で紹介します!
前置きがかなり長くなってしまいましたが、それではPythonでコーディングしていきましょう!
Pythonのlinalgで逆行列を求める
正方行列の場合
PythonではNumPyを使って計算を行います。まずは2×2行列Aを定義します。
inv_Aが逆行列で、np.linalg.inv関数で計算します。ちなみに、linalgは線形代数(Linear Algebra)から来ています。
|
1 2 3 4 5 6 7 8 |
import numpy as np A = np.array([[1, 2], [3, 4]]) # 行列を定義 inv_A = np.linalg.inv(A) # 逆行列を計算 print(A) print(inv_A) print(np.dot(A, inv_A)) |
ちゃんと逆行列が計算されているかは、行列の積を求めて単位行列になっているかどうかで判別しましょう。
しかし、ここで注意ですが、単純にA*inv_Aとしてしまうと、NumPy配列としての計算がされてしまいます。線形代数のルールで行列の積を計算するためには、ベクトルの内積でも使われるnp.dot関数を使用します。
2×2行列同士の積は以下の式(3)で求めることができます。
\[\begin{bmatrix}
a_{1} &a_{2} \\
a_{3} &a_{4}
\end{bmatrix} \times
\begin{bmatrix}
b_{1} &b_{2} \\
b_{3} &b_{4}
\end{bmatrix} =
\begin{bmatrix}
a_{1}b_{1}+a_{2}b_{3} &a_{1}b_{2}+a_{2}b_{4} \\
a_{3}b_{1}+a_{4}b_{3} &a_{3}b_{2}+a_{4}b_{4}
\end{bmatrix} (3)\]
上記コードを実行すると以下の結果を得ます。最後の結果が行列Aに逆行列inv_Aをかけた結果ですが、対角が1でそれ以外が0(実際は数値誤差の影響で左下が0でない非常に小さい値になっていますが)という単位行列になっています。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 行列A [[1 2] [3 4]] # 逆行列inv_A [[-2. 1. ] [ 1.5 -0.5]] # 行列の積の結果 [[1.0000000e+00 0.0000000e+00] [8.8817842e-16 1.0000000e+00]] |
複素数の逆行列も作れる
逆行列は複素数の場合も同様の求め方をします。
以下のコードは複素数に対して逆行列演算を行い、上と同じように内積により単位行列を作る事で検証を行っています。
|
1 |
import numpy as np<br><br># 複素数の変数と行列を定義<br>a = 1 + 1j<br>b = 11 + 11j<br>A = np.array([[a, b], [a, a]]) # 行列を定義<br><br># 逆行列を計算<br>inv_A = np.linalg.inv(A)<br><br># 元行列と逆行列を表示<br>print('A=\n', A)<br>print('A^-1=\n',inv_A)<br><br># 内積を計算して検証<br>print('AA^-1=\n',np.dot(A, inv_A)) |
以下が結果です。複素数でも問題なく逆行列ができています。
|
1 2 3 4 5 6 7 8 9 |
A= [[ 1. +1.j 11.+11.j] [ 1. +1.j 1. +1.j]] A^-1= [[-0.05+0.05j 0.55-0.55j] [ 0.05-0.05j -0.05+0.05j]] AA^-1= [[ 1.00000000e+00+0.j 2.77555756e-17+0.j] [-8.32667268e-17+0.j 1.00000000e+00+0.j]] |
正方行列でない場合(一般化逆行列)
おまけとして行列Aが正方行列でない場合の逆行列、つまり一般化逆行列のコードを以下に示します。こちらは別記事を考えてますので、参考までに。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import numpy as np # 行列を定義 A = np.array([[2, 3], [1, 4], [2, 1]]) print('rank=', np.linalg.matrix_rank(A)) # 行列のランクを調査 # 一般化逆行列を計算 # 自分で式を立てて求める if A.shape[0] > A.shape[1]: A_ginv_manual = np.dot(np.linalg.inv(np.dot(A.T, A)), A.T) else: A_ginv_manual = np.dot(A.T, np.linalg.inv(np.dot(A, A.T))) # np.linalg.pinvで求める A_ginv_lib = np.linalg.pinv(A) print(A_ginv_manual) print(A_ginv_lib) |
ちなみに、結果は以下。式(11)と式(12)で求めた場合(上)とライブラリで求めた場合(下)で同じ結果が得られました。適当に作った行列なので、行列のランクも調査しています。
|
1 2 3 4 5 |
rank= 2 [[ 0.17777778 -0.24444444 0.44444444] [ 0.03333333 0.26666667 -0.16666667]] [[ 0.17777778 -0.24444444 0.44444444] [ 0.03333333 0.26666667 -0.16666667]] |
まとめ
今回は行列や行列式、逆行列の概要とPythonによるコーディング方法を紹介しました。
この行列計算は各種Pythonによる科学技術計算で多用することになると思いますので、基本のキとしておさえておきましょう!
今回は簡単な計算だけど、行列は技術計算で基本中の基本!取り扱い方法をマスターしておこう!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント