機械学習で応答曲面を求めた後、その曲面(学習済モデル)の最小値や最大値を探査したい場合があります。ここではPythonによる実現の例として、とりあえずPyTorchで機械学習→PlatypusのNSGA-IIで探査といった方法を試してみます。
こんにちは。wat(@watlablog)です。ここではPyTorchとPlatypusで回帰と探査をやってみます!
応答曲面法の概要と探査としての使い所
応答曲面法とは?
応答曲面法(RSM : Response Surface Methotology)とは、シミュレーションや実験によってサンプリングされたデータを使って近似関数を作り、この関数を用いて計算を行う手法の事です。
以下は「Python機械学習!scikit-learnによる重回帰分析」で行った重回帰分析のメリットを説明する図ですが、応答曲面法のメリットも基本的にこれと同じです。
多数のデータが既にある場合で、設計変数間の未知の組み合わせにおける応答が知りたい場合に、まずは重回帰分析が有用な分析手法です。
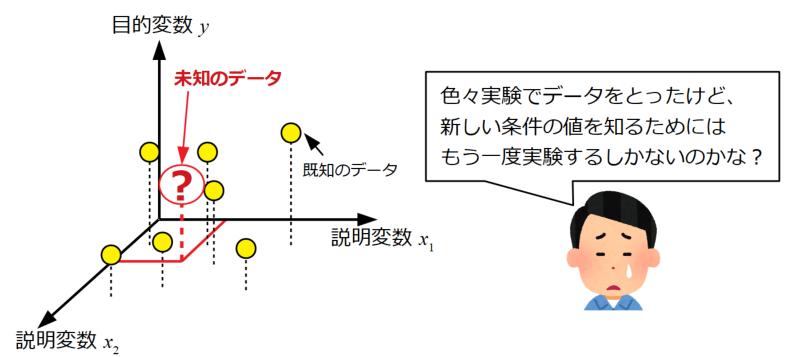
重回帰分析はデータ群に対して平面をフィットさせる手法です。このように平面をモデル(関数)で定義する事ができると、変数の連続的な変化による応答値の予測が可能となります。ちなみに設計変数が3つ以上の場合は超平面となり、もはや図で示す事が困難になります。
応答曲面とは、重回帰分析における平面(または超平面)が曲面になったものと捉えて差し支えありません。
例えば以下の曲面は古典的機械学習の一種であるサポートベクターマシンを回帰モデル構築に利用した例です。データ群に対して曲面をフィッティングさせる事ができています。
※サポートベクターマシンについては以下が参考。
「Pythonサポートベクターマシンで回帰分析!SVRの概要と実装」
「Python機械学習初心者用!サポートベクターマシンの概要と実装」
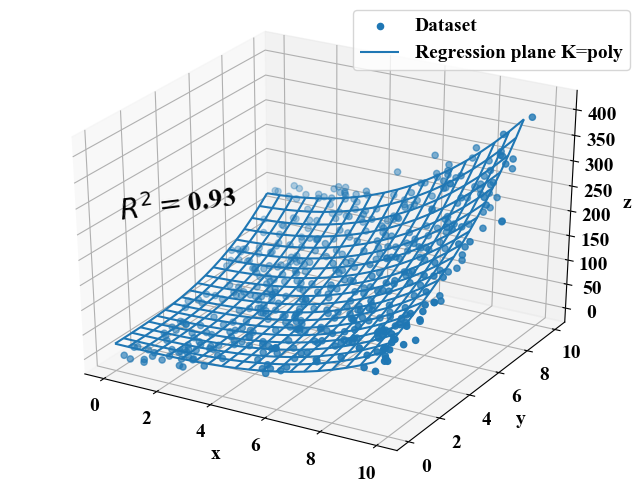
下図のような複雑な曲面もサポートベクターマシンによってフィットさせたものですが、このようにフィットされた曲面(つまりモデル)を使って応答を求める事で、この曲面は応答曲面として活用する事が可能です。
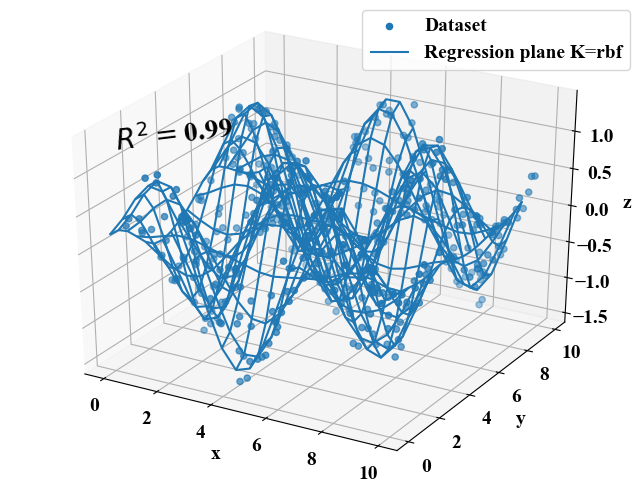
曲面は平面に比べデータにフィットさせる自由度が増えるため、複雑な現象にもフィットする可能性を持ちます。もちろん重回帰分析と同様に設計変数が3つ以上の場合は超曲面で表現する事が可能です(図示は困難ですが)。
全ての応答を物理モデルで求めると時間がかかる
適切なモデルによるシミュレーションや確かな実験をする事で、物理現象に即した応答値を得る事ができます。しかし、より詳細な物理モデルを計算するにはスパコンを使った場合でも数日以上かかるケースがあります。また、実験はそもそも機器が高く、段取り時間が多くかかったり、設計変数を正確かつ自由に振る事が困難であったりします。
単一の応答を得るだけならそれでも我慢できるかも知れませんが、最適化計算のように多目的で多数の計算結果を必要とするような検討には中々踏み込む事ができません。
応答曲面はそのような場合に活用可能です。
下図上段は任意の設計変数を物理モデルに設定して物理シミュレーションを行い、応答値を得る流れを示しています。
この物理モデル(あるいは実験)から少数の応答値をサンプリングし、そのサンプリングデータ点によくフィットするモデル(応答曲面)を使って応答値を得る方法が応答曲面法(下段)です。こうする事で、全ての応答を上段の物理シミュレーションで求めるよりは計算速度が圧倒的に速くなります。
応答曲面はあくまでデータから構成されるため、物理モデルと実験値を併用できる点もメリットの一つです。
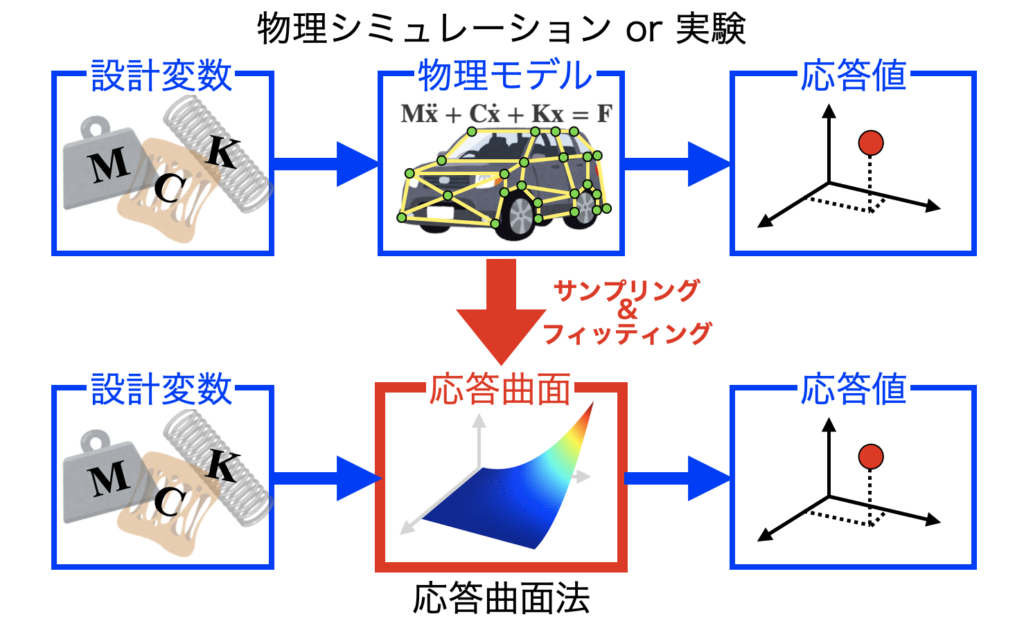
但し、十分な設計空間を網羅していない場合や、サンプリング間隔が粗い場合等は、構築された応答曲面が予測した応答値の精度が著しく落ちてしまう事が注意点です。
応答曲面構築の手段
応答曲面は多数の手法で作成する事が可能です。簡単に列挙するだけでもステップワイズ回帰、フーリエ級数や多項式、様々な関数を使うパラメトリック曲面、ガウシアンプロセス…といった複数の方法があります。
色々ありますが、この記事ではニューラルネットワークによる応答曲面モデルの構築例を紹介します。
但しノーフリーランチ定理があるために応答曲面法も万能ではなく、どのような応答曲面構築手法を使ったとしても、出来上がったモデルの汎化性能が高いかどうかという観点は常に持ち続ける必要があります。
この辺の話は機械学習の勉強をすると嫌というほど出てきますので、是非当ブログの「AI」カテゴリをご覧ください。
設計変数が多いとひと目で最小値がわからない
続いて、応答曲面の最大値や最小値を求める方法(いわゆる最適化)の必要性を説明します。
例えば下図のように設計変数が2つ、応答である特性値が1つの場合は、設計変数をグリッドサーチして3Dプロットをする事でひと目で最大値と最小値を知る事が可能です。
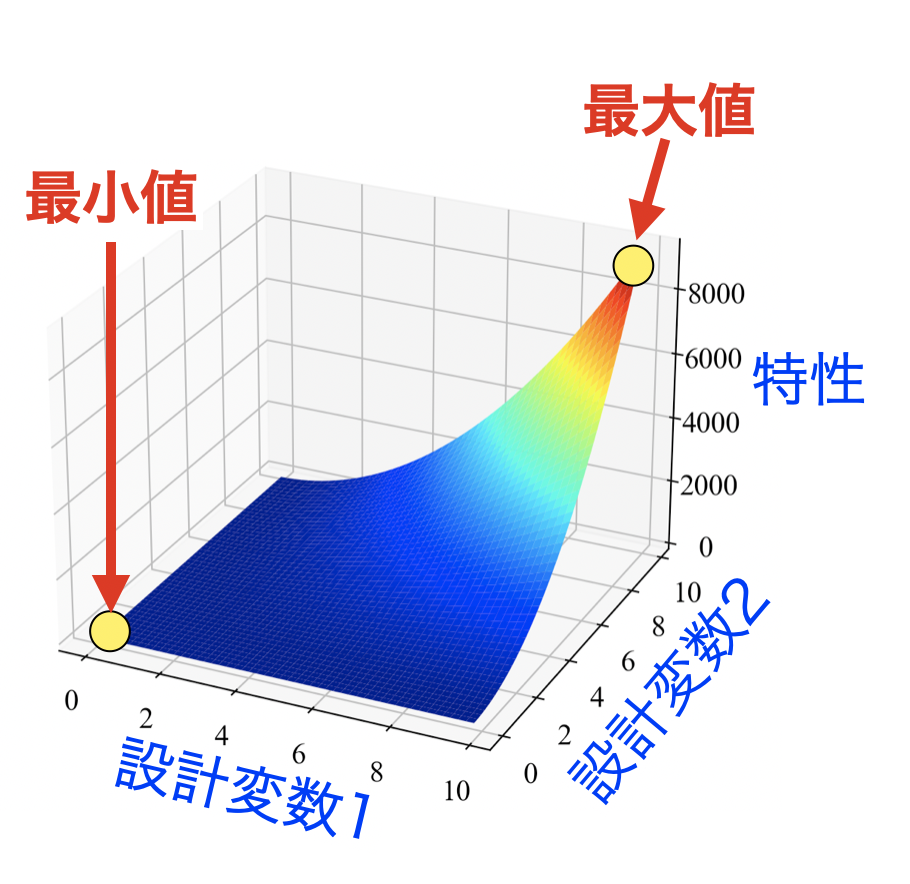
しかしながら、実際の工学の現場では設計変数が3つ以上ある場合、図示できないために簡単には最大値や最小値がわからない問題が多々あります。
このようなケースは、モデルの全貌がわからないために暗闇の中で勾配情報のみを頼りにする方法や、進化的アルゴリズムを使う方法で最大値や最小値を探査する手法がよく使われます。
この記事では後者の1手法であるNSGA-IIを使った方法で探査を行う方法を紹介します。
それでは次の節から、
- ニューラルネットワークで応答曲面を作る
- NSGA-IIで最小値を探査する
2つの方法について、Pythonコードでトライしてみた結果を紹介します。
PyTorchで応答曲面を作るPythonコード
探査するための応答曲面(学習済モデル)を作るために、PyTorchの多層線形ネットワーク回帰コードを紹介します。
参考記事
線形ネットワークによる非線形関数の回帰方法
PyTorchは今ではディープラーニングのフレームワークとして有名になってきました。本記事は応答曲面の作成にこのライブラリを使います。
PyTorchによる線形回帰の方法は以下の記事で紹介していますので、参考にしてください。
「PyTorchで色々な非線形関数を回帰してみたらすごかった」
モデルの保存
PyTorchの学習済モデルはプログラムを終了させるとメモリから解放されてしまう儚い存在です。ファイルに保存していつでも再利用できるようにしておくためにcloudpickleというライブラリを使っています。
Python標準で付いているpickleだとできません。
cloudpickleについては注意点もあるため、「PyTorchモデルをcloudpickleで保存・読み込みする方法」をご覧ください。
学習してモデルを作るためのコード
サンプルの関数
今回は最適化ベンチマークとして使われる関数をトレーニングで回帰しますが、関数は以下のQiita記事を参考にしました(すごく網羅的にまとめられていて大変参考になります!)。
Qiita:最適化アルゴリズムを評価するベンチマーク関数まとめ
この中のFive-Well Potential Functionという次式の多峰性関数を使いました。
すさまじい式です…。
全コード
以下にコピペ動作する全コードを示します。ここでは学習の過程を動画で記録するために「Pythonで複数画像からGIFを作る時に便利な処理まとめ」で紹介した方法でGif画像を作っていますが、動画が必要無い人はこの処理を呼び出さないようにする事で処理時間が速くなります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 |
import torch from torch import nn, optim import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob import cloudpickle # GIFアニメーションを作成 def create_gif(in_dir, out_filename): # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) imgs = [] # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # 線形回帰ネットワークのclassをnn.Moduleの継承で定義 class Regression(nn.Module): # コンストラクタ(インスタンス生成時の初期化) def __init__(self): super().__init__() self.linear1 = nn.Linear(3, 32) self.linear2 = nn.Linear(32, 32) self.linear3 = nn.Linear(32, 16) self.linear4 = nn.Linear(16, 1) # メソッド(ネットワークをシーケンシャルに定義) def forward(self, x): x = nn.functional.relu(self.linear1(x)) x = nn.functional.relu(self.linear2(x)) x = nn.functional.relu(self.linear3(x)) x = self.linear4(x) return x # トレーニング関数 def train(model, optimizer, E, iteration, x, y): # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = model(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print('epoch=', i+1, 'loss=', loss) #グラフ描画用にXY軸とグリッドを作成 X1 = np.arange(-10, 11, 0.5) X2 = np.arange(-10, 11, 0.5) X, Y = np.meshgrid(X1, X2) # データをテンソルに変換(切片用の定数1も結合) X2 = torch.from_numpy(X.ravel().astype(np.float32)).float() Y2 = torch.from_numpy(Y.ravel().astype(np.float32)).float() Input = torch.stack([torch.ones(len(X.ravel())), X2, Y2], 1) # 50計算毎にプロットを保存 if (i + 1) % 100 == 0: Z = test(model, Input).reshape(X.shape) plot_3d(x.T[1], x.T[2], y, X, Y, Z, losses, 'out', i+1) return model, losses # テスト def test(model, x): y_pred = model(x).data.numpy() return y_pred # グラフ描画関数 def plot_3d(x1, x2, z, X, Y, Z, losses, dir, index): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(-20, 20) ax1.set_ylim(-20, 20) ax1.set_zlim(-1, 1) ax2.set_xlim(0, 10000) ax2.set_ylim(0.0001, 100) ax2.set_yscale('log') # データプロット ax1.scatter3D(x1, x2, z, label='dataset') ax1.plot_surface(X, Y, Z, cmap='jet') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses) - 1], color='red') ax2.text(600, 3, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 5, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend(bbox_to_anchor=(0, 1), loc='upper left') fig.tight_layout() # dirフォルダが無い時に新規作成 if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # plt.show() if index == 10000: plt.show() plt.close() plt.close() # ------------------------------------------------------------------- # トレーニングデータ x1 = np.random.uniform(-20, 20, 100) x2 = np.random.uniform(-20, 20, 100) grid_x, grid_y = np.meshgrid(x1, x2) # ノイズを含んだ平面点列データを作成 # Five-well potential function (https://qiita.com/tomitomi3/items/d4318bf7afbc1c835dda) z = ((1 - (1 / (1 + 0.05 * (grid_x ** 2) + (grid_y - 10) ** 2))) - (1 / ((1 + 0.05 * (grid_x - 10) ** 2) + grid_y ** 2)) - (1.5 / ((1 + 0.03 * (grid_x + 10) ** 2) + grid_y ** 2)) - (2 / ((1 + 0.05 * (grid_x - 5) ** 2) + (grid_y + 10) ** 2)) - (1 / ((1 + 0.1 * (grid_x + 5) ** 2) + (grid_y + 10) ** 2))) * (1 + 0.0001 * (grid_x ** 2 + grid_y ** 2) ** 1.2) # テンソル変換とデータ整形 grid_x = torch.from_numpy(grid_x.ravel().astype(np.float32)).float() grid_y = torch.from_numpy(grid_y.ravel().astype(np.float32)).float() z = torch.from_numpy(z.astype(np.float32)).float() X = torch.stack([torch.ones(len(grid_x)), grid_x, grid_y], 1) # ネットワークのインスタンスを生成 net = Regression() # 最適化アルゴリズム(RMSProp)と損失関数(MSE)を設定 optimizer = optim.RMSprop(net.parameters(), lr=0.01) E = nn.MSELoss() # トレーニング net, losses = train(model=net, optimizer=optimizer, E=E, iteration=10000, x=X, y=z) # ネットワークモデルをシリアライズしてファイルに保存 with open('model-A.pt', mode='wb') as f: cloudpickle.dump(net, f) # GIFアニメーションを作成する関数を実行する create_gif(in_dir='out', out_filename='movie.gif') |
出来上がるmovie.gifはこちら。ちょっと見難いですが、データ点に対してうねうねと動いているカラフルな面が学習によってデータにフィットしようとしている応答曲面です。
最小値を表現するために頑張っている様子が確認できますね。
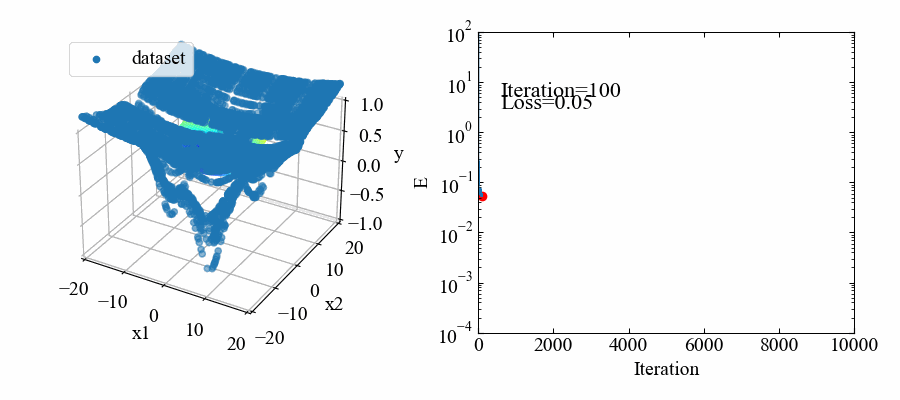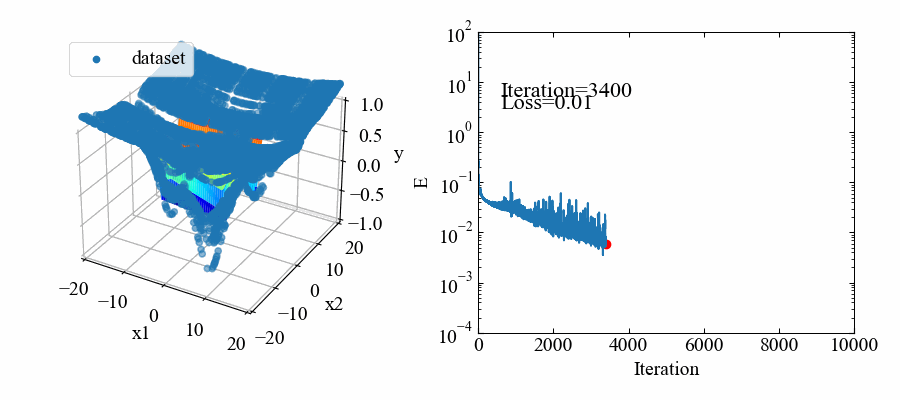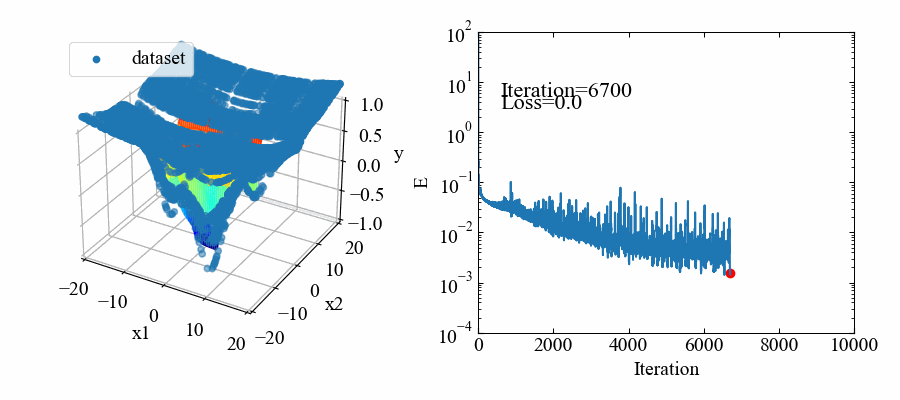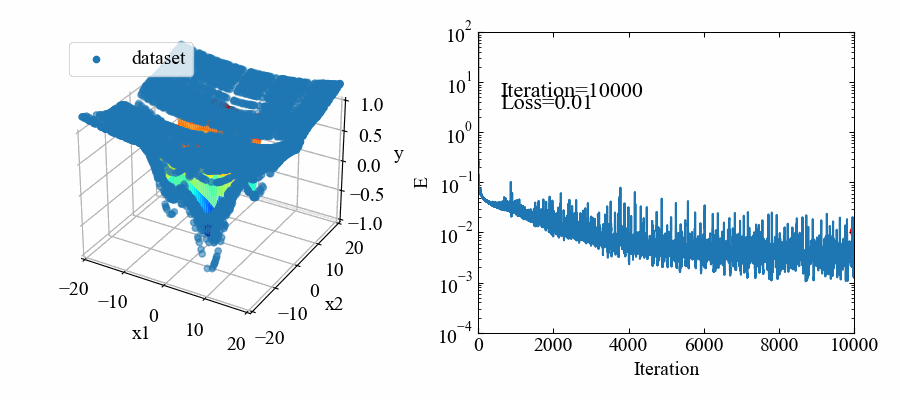
学習済モデルをファイル読み込みして確認するコード
モデルをいきなり探査する前に、せっかく可視化できる次元でトライしているので、先ほど学習した応答曲面モデルを目視で確認してみましょう。
以下がファイル読み込みからプロットするまでのコードです。学習部分を省くとこんだけスリムなコードになるんですね(matplotlibのこだわり部分が長いだけ)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
import cloudpickle import numpy as np import torch from matplotlib import pyplot as plt # ファイルからネットワークモデルをデシリアライズして読み込み with open('model-A.pt', mode='rb') as f: net = cloudpickle.load(f) # グラフ描画用にXY軸とグリッドを作成 X1 = np.arange(-20, 21, 0.1) X2 = np.arange(-20, 21, 0.1) X, Y = np.meshgrid(X1, X2) # データをテンソルに変換(切片用の定数1も結合) X2 = torch.from_numpy(X.ravel().astype(np.float32)).float() Y2 = torch.from_numpy(Y.ravel().astype(np.float32)).float() Input = torch.stack([torch.ones(len(X.ravel())), X2, Y2], 1) # ネットワークモデルから応答を計算 z_pred = net(Input).data.numpy().reshape(X.shape) # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(111, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') # スケール設定 ax1.set_xlim(-20, 20) ax1.set_ylim(-20, 20) ax1.set_zlim(-1, 2) # データプロット ax1.plot_surface(X, Y, z_pred, cmap='jet', alpha=0.5) # グラフを表示する。 fig.tight_layout() plt.show() plt.close() |
下図のように表示されればOK。学習の度合いによって形は崩れると思いますが、今回は1万回のイタレーションで多峰が表現されたのでよしとしましょう。
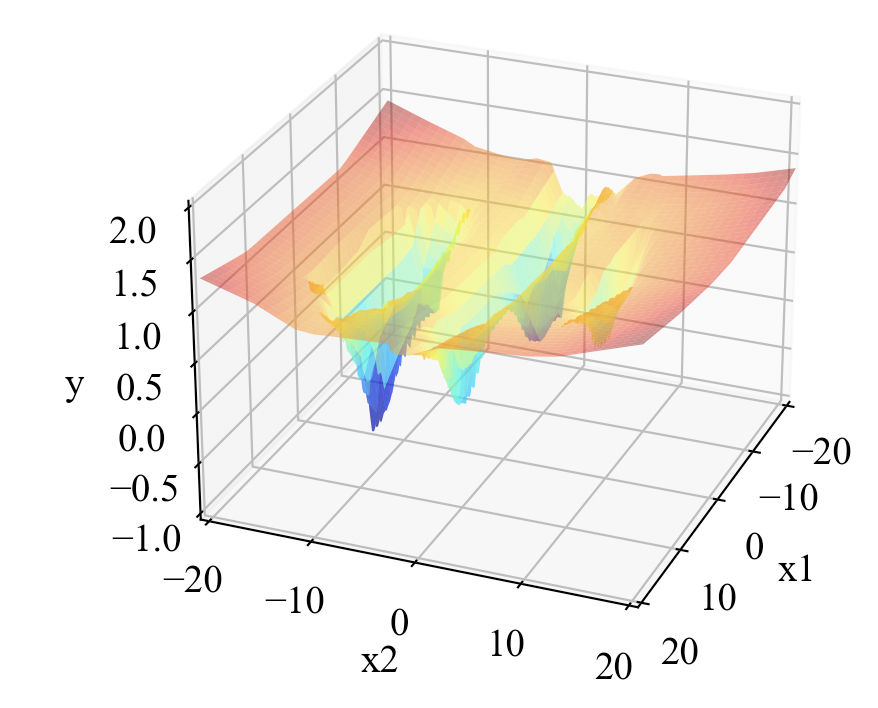
Platypusの遺伝的アルゴリズムで応答曲面を探査するPythonコード
参考記事
Platypusを使った最適化でモデルを探査します。Platypusや最適化については以下の記事を参考にしてください。
「Platypusで多目的最適化からパレートフロントを求める方法」
応答曲面の最小値を探査するコード
先ほど紹介した記事とほぼ同じ構成であるため詳細解説は省きます。注意点は、PyTorchのテンソル型を使ったり応答曲面を作った時のデータshapeに揃えたりする部分です。
先ほど保存したmodel-A.ptを読み込んでNSGA-IIによる最小値探査を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
from platypus import NSGAII, Problem, Real, nondominated from matplotlib import pyplot as plt import cloudpickle import torch import numpy as np # 目的関数(ネットワークモデル) def objective(vars): x = vars[0] y = vars[1] x = torch.tensor(x).float() y = torch.tensor(y).float() Input = torch.stack([torch.tensor(1), x, y], 0) # ファイルからネットワークモデルをデシリアライズして読み込み with open('model-A.pt', mode='rb') as f: net = cloudpickle.load(f) # ネットワークモデルから応答を計算 f1 = net(Input).data.numpy() return [f1] # 最適化計算を実行する関数 def optimization(n_var, n_obj, vars, n_run): # 設計変数と目的関数の数を設定 problem = Problem(n_var, n_obj) # 最適化問題に最小化を設定 problem.directions[:] = Problem.MINIMIZE # 設計変数と目的関数を設定 problem.types[:] = vars problem.function = objective # 最適化アルゴリズムを設定して計算を実行する algorithm = NSGAII(problem) algorithm.run(n_run) return algorithm # 変数を設定する var1 = Real(-20., 20.) var2 = Real(-20., 20.) vars = [var1, var2] # 最適化計算を実行する algorithm = optimization(n_var=len(vars), n_obj=1, vars=vars, n_run=10) # ここからグラフ描画-------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = fig.add_subplot(111, projection='3d') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('f1') ax1.set_xlim(-20, 20) ax1.set_ylim(-20, 20) ax1.set_zlim(-1, 2) def test(): # グラフ描画用にXY軸とグリッドを作成 X1 = np.arange(-20, 21, 0.5) X2 = np.arange(-20, 21, 0.5) X, Y = np.meshgrid(X1, X2) # データをテンソルに変換(切片用の定数1も結合) X2 = torch.from_numpy(X.ravel().astype(np.float32)).float() Y2 = torch.from_numpy(Y.ravel().astype(np.float32)).float() Input = torch.stack([torch.ones(len(X.ravel())), X2, Y2], 1) # ファイルからネットワークモデルをデシリアライズして読み込み with open('model-A.pt', mode='rb') as f: net = cloudpickle.load(f) # ネットワークモデルから応答を計算 Z = net(Input).data.numpy().reshape(X.shape) return X, Y, Z X, Y, Z = test() # データプロット for solution in algorithm.result: ax1.scatter3D(solution.variables[0], solution.variables[1], solution.objectives[0], color='yellow', edgecolor='black', s=30) print(solution.variables[0], solution.variables[1], solution.objectives[0]) ax1.plot_surface(X, Y, Z, cmap='jet', alpha=0.5) # グラフを表示する。 plt.show() plt.close() # ---------------------------------------------------------- |
以下が結果です。おしい点がいくつかあるようですが、急峻な峰の探査は結構難しいのかも知れませんね。
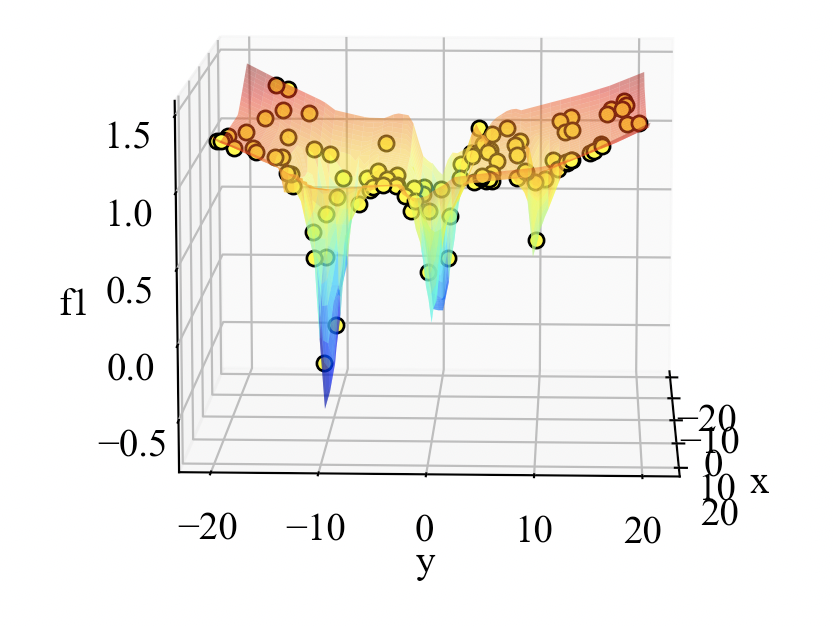
特定の設計変数のペアを抽出したい時は、algorithm.resultをforループで回している部分でsolution.objectives[0]の値を基準にすれば良さそうです。
一度配列に格納、ソートすることで目的関数が最小値になる設計変数を抽出する事が可能です。
まとめ
本記事ではこの分野の初心者がPythonを使って応答曲面を作ったり、作った応答曲面を探査したりするコードを紹介しました。
もっと複雑なデータでトライしようと思いましたが、まず第一歩としては目視で確認できる次元の範囲でやってみました。
まだまだ実問題に適用するには課題がいくつかありそうです…。
PyTorchとPlatypusを連携させたいがための記事を書いてみました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!