Platypusで多目的最適化からパレートフロントを求める方法

多目的最適化とは、2つ以上のトレードオフ関係にある複数の目的関数を同時に最適化する方法の事です。ここではPythonライブラリであるPlatypusを使って簡単な多目的最適化を行い、パレートフロントを求めるコードを紹介します。

こんにちは。wat(@watlablog)です。ここではPlatypusというライブラリを使って多目的最適化からパレート解を求めてみます！

前半は用語の整理や勉強用につらつらと長ったらしく文章を書いています。てっとり早くコードを見たい方は目次からジャンプしてください！

目次（項目クリックでジャンプできます）

最適化問題の概要

最適化とは？

ここで言う最適化(Optimization)とは、複数の選択肢の中から最も良い解を見つける事を意味します。

最も理解しやすい最適化問題の例としては、最小二乗法のような二乗誤差を最小にする問題が挙げられます。

下図は変数\(x\)を振って、誤差関数\(f(x)\)の値\(Loss\)を最小にする問題を表現しています。現在の位置から始めたとして、勾配を登る方向に\(x\)を動かすと誤差は大きくなってしまいますが、勾配を降下する方向に\(x\)を動かすと誤差が小さくなります。ここで、この下に凸の関数の最小値を最適解と呼びます。そして最適解を求めるために最小化（または最大化）する関数を目的関数と呼びます。

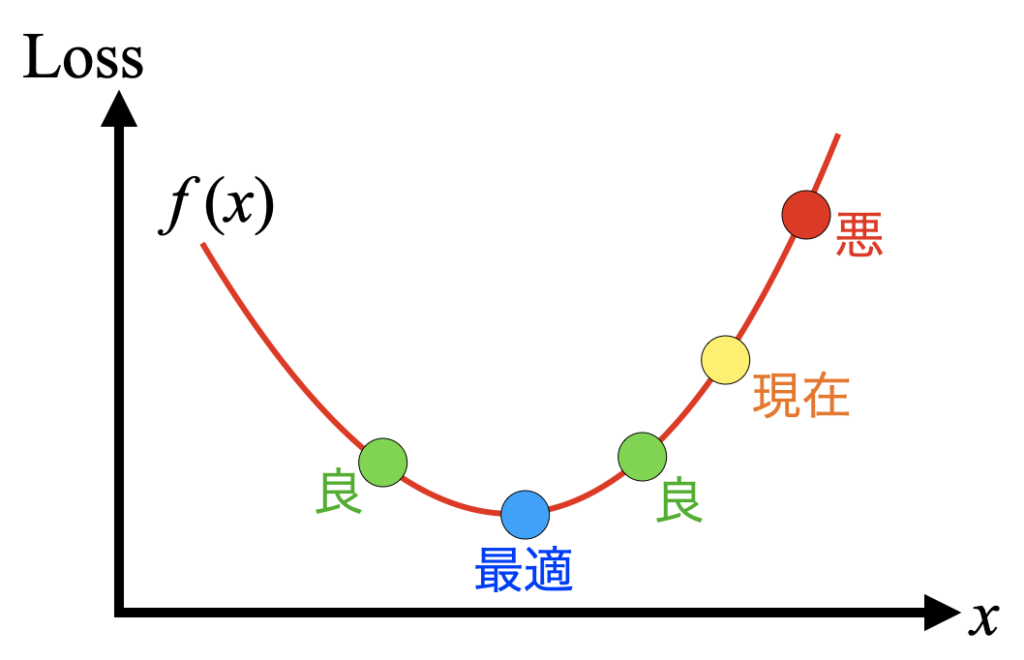
最小二乗法のような簡単な問題は「Pythonでカーブフィット!最小二乗法で直線近似する方法」で紹介したように数式的に解を求める事が可能です。

また、このような最小値を求める方法には「Pythonで1変数と2変数関数の勾配降下法を実装してみた」で紹介した勾配降下法という手法も有効です。

勾配降下法は学習率の設定がシビアであったり、最小値を求めるのに時間がかかったりするため、MomentumやAdaGrad、RMSProp…とその他様々な改良手法が開発されています。

…様々な手法がありますが、下図のように本当に最小である大域的最適解ではなく、局所最適解や停留点にトラップされるという問題は常に考えなければなりません。

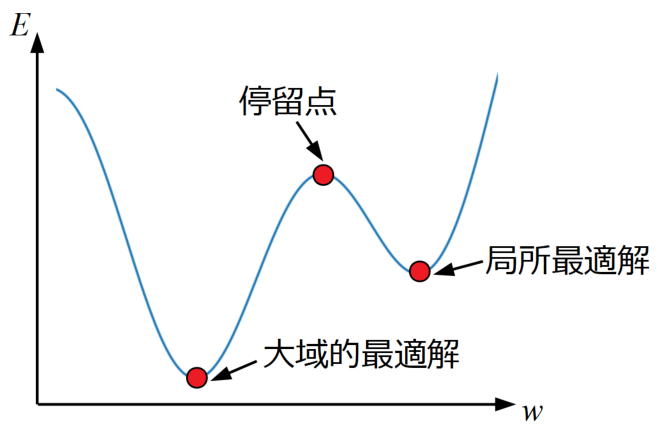
とはいえ、局所最適解でも設定された要件を満足する場合が多いので、これらの最適化手法は一般によく使われています。

多目的最適化

定式化

関数形がわからない場合、単一の目的関数の最小値を求めるだけでも難しい問題ですが、今回この記事で扱うのは複数の目的関数を同時に最適化する多目的最適化問題です。

一般に多目的最適化(Multiobjective Optimization)は、\(n\)個の設計変数\(x_{n}\)で構成された\(k\)個の目的関数\(f_{i}\)を、\(m\)個の不等式制約条件\(v_{j}\)の元で最小化（または最大化）する問題として次式で定式化されます。

\[ \begin{eqnarray} &f_{i}&(x_{1}, x_{2}, \dots, x_{n})\hspace{25pt}(i=1, 2, \dots, k)\\ &v_{j}&(x_{1}, x_{2}, \dots, x_{n})\leq 0\hspace{10pt}(j=1, 2, \dots, m) \end{eqnarray} \]

多目的最適化の例

多目的最適化問題の例として、下図のような多目的ナップザック問題が有名です。

ピクニックではナップザックに必要な物やおやつを詰めて行きますが、ナップザックにはなんでもかんでも入るわけではありません。

満足度の高いおやつを最大限持っていきたい気持ちと、旅のリスクを最小限にするための持ち物を有限の容積の範囲で選択する必要があります。

また、学校行事の場合はおやつの金額制限（今でもあるのかは不明）もあるかも知れません。

これはナップザックの容積とおやつの金額という制約条件を満たしつつ、おやつの価値という目的関数を最大化、リスクという目的関数を最小化する多目的最適化問題と捉える事が出来ます。

例えば車両の開発では燃費や電費、その他諸性能という目的関数をコストや重量といった様々な制約条件のもとで最適化する問題と捉える事が出来ます。

このように世の中は多目的最適化問題で溢れており、最適化を行う手法の開発が盛んに行われています。

パレート解

複数の目的関数は通常それぞれがトレードオフ関係にあるため、全ての目的関数が同時に最小値になる事はありません。これは最適な選択肢が一つに決まらない事を意味しています。

そこで、パレート解という概念を導入する必要があります。

下図は2つの目的関数について、一方を最小化、他方を最大化する場合の最適化問題を表現しています。製品設計を行う場面を想定します。

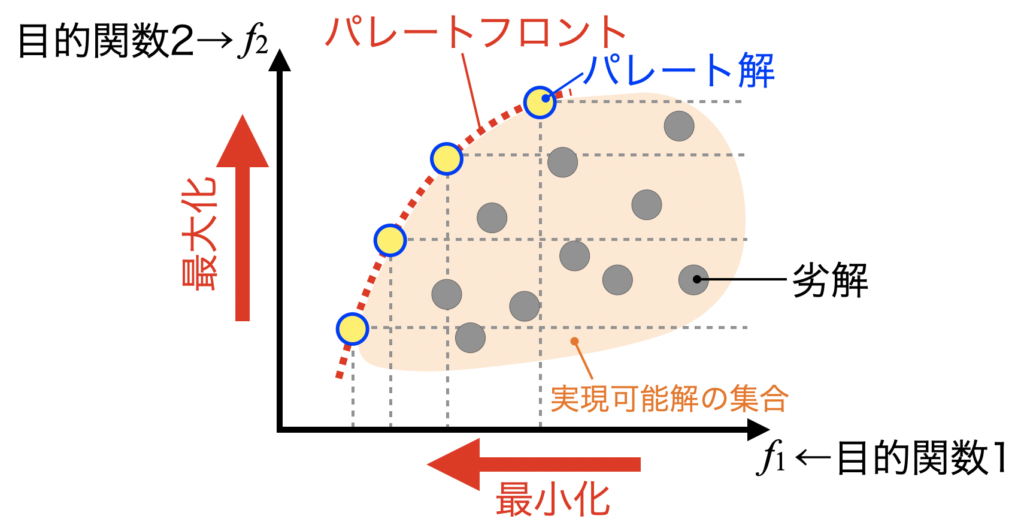
多目的最適化問題を計算すると、実際に設計可能な実現可能解(Feasible solution)の集合を得ます。

この解集合をより最適な方向（この例では左上）に拡げる事ができると、それまで得られていた解より優れた解が見つかってきます。

一度優れた解が見つかると、それまでの解は劣解(Inferior solution)となります。最終的に劣解とならない解の事を非劣解、またはパレート解(Pareto solution)と呼びます。

この優れた解であるパレート解のライン(赤点線)をパレートフロント(Pareto front)と呼び、トレードオフ関係を表現しているパレートフロントを求める事こそが多目的最適化の一つのゴールと言えます。

選好解

パレートフロントを求める事は最適化問題の一つのゴールですが、それだけだと今回想定している設計までは完了しません。設計者にはこの中からただ一つの解を選択して設計フェーズを一歩進める事が求められます。

通常は会議等を行い、様々な要因を考慮して解を選択しますが、この時選ばれたパレート解の一つを選好解(Preference solution)と呼びます。

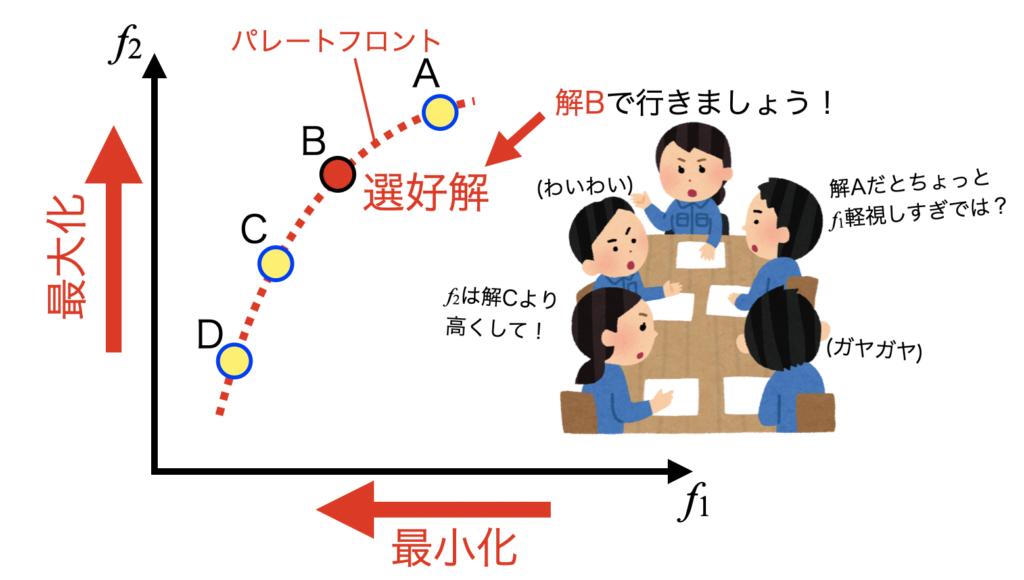
仮にこの選好解が何らかの理由で採用できなくなった時も、一度最適化計算を実行してパレートフロントを求めておくと代替案を即座に用意する事ができるようになります。

多目的最適化問題にPlatypusを使う

進化アルゴリズム

この記事では多目的最適化問題の例題を、多目的進化アルゴリズム(MOEA : Multi Objective Evolutionary Algorithm)で計算してみます。

進化アルゴリズムとは生態系の遺伝や進化を模倣して最適解を探査する手法の事です。

遺伝的アルゴリズム(GA : Genetic Algorithm)もこの手法に分類され、評価値の算出、遺伝子交叉、自然淘汰、適者生存といったプロセスを経て最適解を探すため、メタヒューリスティックな手法と言えます。

多目的最適化アルゴリズムには非常に様々な手法があり、内容も難しいのでこの記事では詳細を書きません（まだ書けません！）。

詳細は専門書に任せるとして、一般ユーザとしてはソフトウェアに計算を任せる方針をとります。

Platypus

今回はPythonで使える多目的最適化ライブラリとしてPlatypusを紹介します。

PlatypusにはNSGA-II, NSGA-III, CMAES, GDE3, IBEA, MOEAD, OMOPSO, SMPSO, SPEA2, EpsMOEAといった様々なアルゴリズムが実装されています。

詳細は以下の公式ドキュメントをご確認ください。

公式ドキュメント：Platypus

インストール

Platypusはpipから簡単にインストール可能です。「-opt」をつけ忘れないよう注意してください。

# Windows
python -m pip install platypus-opt

# Mac
pip3 install platypus-opt

# Windows

python -m pip install platypus-opt

# Mac

pip3 install platypus-opt

Platypusでパレートフロントを求めるPythonコード

検証した動作環境

今回検証した動作環境を以下にメモしておきます。

PC

Windows	OS	Windows10 64bit
	CPU	Intel 11th Core i7-11800H:2.3[GHz]
	メモリ	16[GB]

Mac	OS	macOS Catalina 10.15.7
	CPU	1.4[GHz]
	メモリ	8[GB]

Python環境

Python	Python 3.9.6
PyCharm (IDE)	PyCharm CE 2020.1
matplotlib	3.4.3
Platypus-Opt	1.0.4

【制約条件無し】2変数2目的の多目的最適化問題を解く例

問題設定

まずは制約条件の無い2変数2目的の多目的最適化問題の例題を設定します。

次式で設定する\(f_{1}\)と\(f_{2}\)を共に最小化します。ここで変数\(x, y\)の範囲は\(\in\)記号（「属する」という意味）で指定しています。

\[ \begin{cases} \mathrm{minimize} \hspace{5pt} f_{1}&=&x^{2} + y^{2}　\\ \mathrm{minimize} \hspace{5pt} f_{2}&=&(x-5)^{2}+(y-5)^{2} \end{cases}\\ \mathrm{for} \hspace{5pt} x \in [-5, 5], y \in [-5, 5] \]

目的関数を設定するコード

Platypusで最適化を行う場合の書き方、お作法を整理していきます。

まず、目的関数はdef文で本当に関数として定義し、引数にリスト形式の変数、returnにリスト形式で全目的関数を設定します。

あとは内部で変数を分解し、冒頭の式をそのまま記述します。

# 目的関数
def objective(vars):
    x = vars[0]
    y = vars[1]
    f1 = x ** 2 + y ** 2
    f2 = (x - 5) ** 2 + (y - 5) ** 2
    return [f1, f2]

# 目的関数

def objective(vars):

x = vars[0]

y = vars[1]

f1 = x ** 2 + y ** 2

f2 = (x - 5) ** 2 + (y - 5) ** 2

return [f1, f2]

import文と問題を設定するコード

importにはplatypusの中から最適化アルゴリズムのNSGA-II、問題設定用のProblem、型定義用のReal（実数。整数ならInteger）、非劣解抽出用のnondominatedをまとめて定義します。

そして最適化計算を行うために、まずはProblemで問題定義を行います。今回は2変数2目的なので、以下コードで変数の数と目的関数の数を(2, 2)と定義しています。

from platypus import NSGAII, Problem, Real, nondominated

# 設計変数と目的関数の数を設定
problem = Problem(2, 2)

from platypus import NSGAII, Problem, Real, nondominated

# 設計変数と目的関数の数を設定

problem = Problem(2, 2)

目的関数の最小化設定をするコード

問題クラスからdirectionsを呼び出し、最小化（MINIMIZE）を設定します。ここではスライスで一括指定していますが、個別に最大化や最小化を別々に設定する事も可能です。

# 最適化問題に最小化を設定
problem.directions[:] = Problem.MINIMIZE

1 2	# 最適化問題に最小化を設定 problem.directions[:] = Problem.MINIMIZE

設計変数と目的関数をセットするコード

以下のように設計変数を型付きで定義し、リスト形式にまとめ、typesとfunctionで変数と目的関数を問題内に組み込みます。typesもスライス一括指定していますが、先ほどと同様に個別に変数を設定する事が可能です。

# 変数を設定する
var1 = Real(-5., 5.)
var2 = Real(-5., 5.)
vars = [var1, var2]

# 設計変数と目的関数を設定
problem.types[:] = vars
problem.function = objective

# 変数を設定する

var1 = Real(-5., 5.)

var2 = Real(-5., 5.)

vars = [var1, var2]

# 設計変数と目的関数を設定

problem.types[:] = vars

problem.function = objective

最適化アルゴリズムを設定して計算実行するコード

今回は多目的進化アルゴリズムの一種であるNSGA-II(Non-dominated Sorting Genetic Algorithms-II)を使います。

アルゴリズムは既にPlatypusで用意されているので、NSGAII()に問題を引数として与えるだけで設定完了です。

最後に、計算数を指定してrunで実行します。

# 最適化アルゴリズムを設定して計算を実行する
algorithm = NSGAII(problem)
algorithm.run(10)

# 最適化アルゴリズムを設定して計算を実行する

algorithm = NSGAII(problem)

algorithm.run(10)

公式ドキュメントによると、PlatypusでNSGA-IIを使った時はユーザが詳細の設定を指定しなくても、問題に適した設定を提供してくれるようです（!）。

Note that we did not need to specify many settings when constructing NSGA-II. For any options not specified by the user, Platypus supplies the appropriate settings using best practices.
Platypus:Getting started

NSGAII(problem, population_size=100)とかで初期世代を設定する事もできるけど、問題の種類を判定して自動設定してくれるとのこと。
こういう最適化問題は設計変数や目的関数の数、問題の凸加減とかで最適設定があるのかな？この辺は論文読まなきゃわからなそう。

実現可能解とパレート解の抽出

実現可能解の集合を可視化したい時は、.resultで計算結果を受け取り、objectivesから抽出可能です。ここでは2目的あるので、obj1, obj2と二つの変数に格納しています。

# 最適化結果から実現可能解をプロットする。
obj1 = []
obj2 = []
for solution in algorithm.result:
    obj1.append(solution.objectives[0])
    obj2.append(solution.objectives[1])

# 最適化結果から実現可能解をプロットする。

obj1 = []

obj2 = []

for solution in algorithm.result:

obj1.append(solution.objectives[0])

obj2.append(solution.objectives[1])

パレート解も同様の感覚で抽出します。一度nondominated()で支配された解を取り除く（＝劣解を取り除く＝パレート解を抽出）事が必要です。

# パレート解をプロットする。
n_dominated = nondominated(algorithm.result)    # 非劣解を抽出する
obj1 = []
obj2 = []
for solution in n_dominated:
    obj1.append(solution.objectives[0])
    obj2.append(solution.objectives[1])

# パレート解をプロットする。

n_dominated = nondominated(algorithm.result) # 非劣解を抽出する

obj1 = []

obj2 = []

for solution in n_dominated:

obj1.append(solution.objectives[0])

obj2.append(solution.objectives[1])

全コード（関数化とプロット付き）

以下にコピペ動作する全コードを示します。先ほどは説明上個別にコードを紹介しましたが、ここでは最適化計算部分もdef関数化したり、各数値を変数化したりしています。

そして最後にmatplotlibによるプロットもしていますので、コードをご確認ください。

from platypus import NSGAII, Problem, Real, nondominated
from matplotlib import pyplot as plt

# 目的関数
def objective(vars):
    x = vars[0]
    y = vars[1]
    f1 = x ** 2 + y ** 2
    f2 = (x - 5) ** 2 + (y - 5) ** 2
    return [f1, f2]

# 最適化計算を実行する関数
def optimization(n_var, n_obj, vars, n_run):
    # 設計変数と目的関数の数を設定
    problem = Problem(n_var, n_obj)

    # 最適化問題に最小化を設定
    problem.directions[:] = Problem.MINIMIZE

    # 設計変数と目的関数を設定
    problem.types[:] = vars
    problem.function = objective

    # 最適化アルゴリズムを設定して計算を実行する
    algorithm = NSGAII(problem)
    algorithm.run(n_run)

    return algorithm

# 変数を設定する
var1 = Real(-5., 5.)
var2 = Real(-5., 5.)
vars = [var1, var2]

# 最適化計算を実行する
algorithm = optimization(n_var=len(vars), n_obj=2, vars=vars, n_run=10)

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# グラフの入れ物を用意する。
fig = plt.figure(figsize=(6, 5))
ax1 = fig.add_subplot(111)

# 軸のラベルを設定する。
ax1.set_xlabel('Objective1')
ax1.set_ylabel('Objective2')

# 最適化結果から実現可能解をプロットする。
obj1 = []
obj2 = []
for solution in algorithm.result:
    obj1.append(solution.objectives[0])
    obj2.append(solution.objectives[1])
ax1.scatter(obj1, obj2, color='gray', edgecolor='gray', label='Trial', alpha=0.5)

# パレート解をプロットする。
n_dominated = nondominated(algorithm.result)    # 非劣解を抽出する
obj1 = []
obj2 = []
for solution in n_dominated:
    obj1.append(solution.objectives[0])
    obj2.append(solution.objectives[1])
ax1.scatter(obj1, obj2, color='yellow', edgecolor='black', label='Pareto front')
ax1.legend()

# グラフを表示する。
plt.show()
plt.close()

from platypus import NSGAII, Problem, Real, nondominated

from matplotlib import pyplot as plt

# 目的関数

def objective(vars):

x = vars[0]

y = vars[1]

f1 = x ** 2 + y ** 2

f2 = (x - 5) ** 2 + (y - 5) ** 2

return [f1, f2]

# 最適化計算を実行する関数

def optimization(n_var, n_obj, vars, n_run):

# 設計変数と目的関数の数を設定

problem = Problem(n_var, n_obj)

# 最適化問題に最小化を設定

problem.directions[:] = Problem.MINIMIZE

# 設計変数と目的関数を設定

problem.types[:] = vars

problem.function = objective

# 最適化アルゴリズムを設定して計算を実行する

algorithm = NSGAII(problem)

algorithm.run(n_run)

return algorithm

# 変数を設定する

var1 = Real(-5., 5.)

var2 = Real(-5., 5.)

vars = [var1, var2]

# 最適化計算を実行する

algorithm = optimization(n_var=len(vars), n_obj=2, vars=vars, n_run=10)

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# グラフの入れ物を用意する。

fig = plt.figure(figsize=(6, 5))

ax1 = fig.add_subplot(111)

# 軸のラベルを設定する。

ax1.set_xlabel('Objective1')

ax1.set_ylabel('Objective2')

# 最適化結果から実現可能解をプロットする。

obj1 = []

obj2 = []

for solution in algorithm.result:

obj1.append(solution.objectives[0])

obj2.append(solution.objectives[1])

ax1.scatter(obj1, obj2, color='gray', edgecolor='gray', label='Trial', alpha=0.5)

# パレート解をプロットする。

n_dominated = nondominated(algorithm.result) # 非劣解を抽出する

obj1 = []

obj2 = []

for solution in n_dominated:

obj1.append(solution.objectives[0])

obj2.append(solution.objectives[1])

ax1.scatter(obj1, obj2, color='yellow', edgecolor='black', label='Pareto front')

ax1.legend()

# グラフを表示する。

plt.show()

plt.close()

実行結果

以下がコードの実行結果です。実現可能解とパレート解のプロット結果となります。

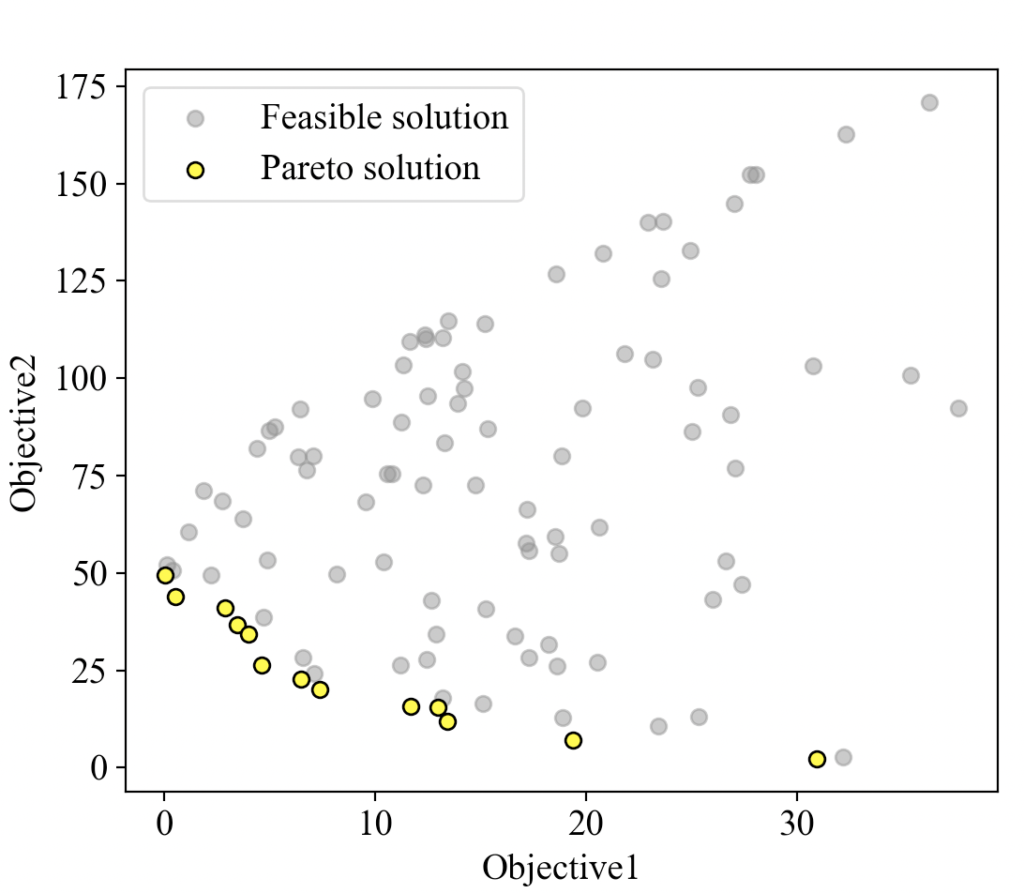
今回は2つの目的関数(グラフの横軸と縦軸)を共に最小化しているので、左下にパレート解が集まりました。実現可能解の中でグレーの点は劣解であり、いずれかのパレート解に支配されている様子が確認できます。

おまけ：解の設計変数を抽出する

パレート解のプロットを見ただけでは設計できないので、設計変数値と目的関数値をそれぞれ抽出する事も必要です。

以下のように.variablesを使う事で設計変数値を抽出する事ができるので、この値をスプレッドシート等にまとめておくと良いかも知れません。

# パレート解をプロットする。
n_dominated = nondominated(algorithm.result)    # 非劣解を抽出する
obj1 = []
obj2 = []
for solution in n_dominated:
    obj1.append(solution.objectives[0])
    obj2.append(solution.objectives[1])
    print('Variables=', solution.variables[0], solution.variables[1], 'Objectives=', solution.objectives[0], solution.objectives[1])

# パレート解をプロットする。

n_dominated = nondominated(algorithm.result) # 非劣解を抽出する

obj1 = []

obj2 = []

for solution in n_dominated:

obj1.append(solution.objectives[0])

obj2.append(solution.objectives[1])

print('Variables=', solution.variables[0], solution.variables[1], 'Objectives=', solution.objectives[0], solution.objectives[1])

以下のように出力されます。

Variables= 1.8756991850459386 3.377122739730753 Objectives= 14.923205431988546 12.39498618422163
Variables= 1.4021982554913723 1.1718010724923023 Objectives= 3.3392777011971573 27.599284421360412
Variables= 3.7027380288424094 4.56194581501231 Objectives= 34.521618529344096 1.874780090796907
Variables= 2.988776741061905 0.9331604572067889 Objectives= 9.803574846807004 20.584202864120066
.
.
.

Variables= 1.8756991850459386 3.377122739730753 Objectives= 14.923205431988546 12.39498618422163

Variables= 1.4021982554913723 1.1718010724923023 Objectives= 3.3392777011971573 27.599284421360412

Variables= 3.7027380288424094 4.56194581501231 Objectives= 34.521618529344096 1.874780090796907

Variables= 2.988776741061905 0.9331604572067889 Objectives= 9.803574846807004 20.584202864120066

【制約条件付き】2変数2目的の多目的最適化問題を解く例

問題設定

続いて不等式制約条件を付けた問題を扱います。

次式\(\mathrm{subject}\hspace{2pt}\mathrm{to}\)の部分が制約条件です。\(x+y\leq 3\)を書きたい場合、右辺を0にするように移項した書き方をします。

その他の目的関数や設計変数の範囲は先ほどと同様です。

\[ \begin{cases} \mathrm{minimize} \hspace{5pt} &f_{1}&=x^{2} + y^{2}　\\ \mathrm{minimize} \hspace{5pt} &f_{2}&=(x-5)^{2}+(y-5)^{2}\\ \mathrm{subject}\hspace{5pt}\mathrm{to} \hspace{10pt} x + y &- 3&\leq0　 \end{cases}\\ \mathrm{for} \hspace{5pt} x \in [-5, 5], y \in [-5, 5] \\ \]

制約条件の付け方

コード部分は変化点を記載します。まず、以下の目的関数部分では、先ほどの不等式制約条件式の左辺をv1で定義します。

# 目的関数
def objective(vars):
    x = vars[0]
    y = vars[1]
    f1 = x ** 2 + y ** 2
    f2 = (x - 5) ** 2 + (y - 5) ** 2
    v1 = x + y - 3
    return [f1, f2], [v1]

# 目的関数

def objective(vars):

x = vars[0]

y = vars[1]

f1 = x ** 2 + y ** 2

f2 = (x - 5) ** 2 + (y - 5) ** 2

v1 = x + y - 3

return [f1, f2], [v1]

最適化計算部分は、まずProblemの第3引数に制約条件の個数n_con(ここではn_con=1)を追加します。次に.constraintsを設定します。

# 最適化計算を実行する関数
def optimization(n_var, n_obj, n_con, vars, n_run):
    # 設計変数と目的関数の数を設定
    problem = Problem(n_var, n_obj, n_con)

    # 最適化問題に最小化を設定
    # 制約条件を設定
    problem.directions[:] = Problem.MINIMIZE
    problem.constraints[:] = "<=0"

    # 設計変数と目的関数を設定
    problem.types[:] = vars
    problem.function = objective

    # 最適化アルゴリズムを設定して計算を実行する
    algorithm = NSGAII(problem)
    algorithm.run(n_run)

    return algorithm

# 最適化計算を実行する関数

def optimization(n_var, n_obj, n_con, vars, n_run):

# 設計変数と目的関数の数を設定

problem = Problem(n_var, n_obj, n_con)

# 最適化問題に最小化を設定

# 制約条件を設定

problem.directions[:] = Problem.MINIMIZE

problem.constraints[:] = "<=0"

# 設計変数と目的関数を設定

problem.types[:] = vars

problem.function = objective

# 最適化アルゴリズムを設定して計算を実行する

algorithm = NSGAII(problem)

algorithm.run(n_run)

return algorithm

実行結果（制約条件を変更して比較）

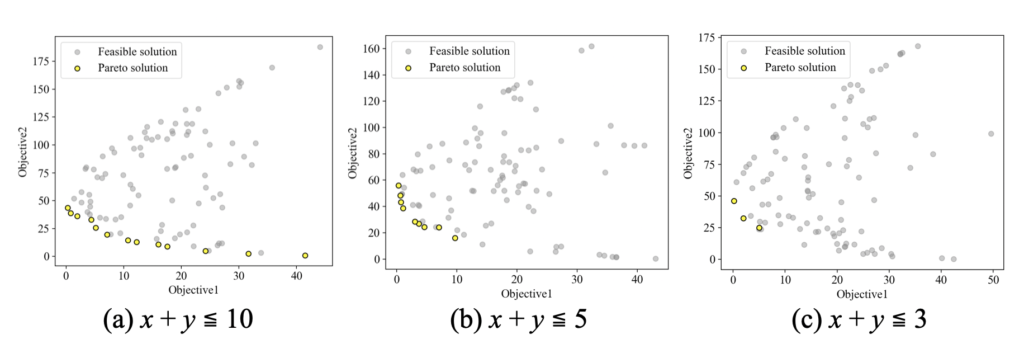
以下が実行結果です。(c)の結果が上記問題設定の結果ですが、(a), (b)のような条件にすると制約条件無しの結果に近づきます。元々の変数の範囲が5までなので、これは当然の結果と考えられます。

まとめ

本記事では多目的最適化の概要として、実現可能解、解集合、劣解、パレート解、パレートフロントといった用語を調べてみました。また、PlatypusというPythonライブラリを使って2変数2目的の多目的最適化問題をNSGA-IIで計算してみました。

最適化アルゴリズムは自分で実装するのが大変ですが、ライブラリを使う事で誰でも簡単に利用する事ができるようです。
…とは言え中身の勉強は地道にしていきたいと思います。

今回ライブラリを使った設計変数、目的関数、制約条件の設定方法がわかってきたので、ゆくゆくは機械学習モデル、シミュレーションモデルといった実用的なケースに適用してみようと思います。

最適化計算ライブラリは工学系の武器としては応用範囲が広そうです！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

最適化問題の概要

最適化とは？

多目的最適化

定式化

多目的最適化の例

パレート解

選好解

多目的最適化問題にPlatypusを使う

進化アルゴリズム

Platypus

インストール

Platypusでパレートフロントを求めるPythonコード

検証した動作環境

PC

Python環境

【制約条件無し】2変数2目的の多目的最適化問題を解く例

問題設定

目的関数を設定するコード

import文と問題を設定するコード

目的関数の最小化設定をするコード

設計変数と目的関数をセットするコード

最適化アルゴリズムを設定して計算実行するコード

実現可能解とパレート解の抽出

全コード（関数化とプロット付き）

実行結果

おまけ：解の設計変数を抽出する

【制約条件付き】2変数2目的の多目的最適化問題を解く例

問題設定

制約条件の付け方

実行結果（制約条件を変更して比較）

まとめ

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

最適化問題の概要

最適化とは？

多目的最適化

定式化

多目的最適化の例

パレート解

選好解

多目的最適化問題にPlatypusを使う

進化アルゴリズム

Platypus

インストール

Platypusでパレートフロントを求めるPythonコード

検証した動作環境

PC

Python環境

【制約条件無し】2変数2目的の多目的最適化問題を解く例

問題設定

目的関数を設定するコード

import文と問題を設定するコード

目的関数の最小化設定をするコード

設計変数と目的関数をセットするコード

最適化アルゴリズムを設定して計算実行するコード

実現可能解とパレート解の抽出

全コード（関数化とプロット付き）

実行結果

おまけ：解の設計変数を抽出する

【制約条件付き】2変数2目的の多目的最適化問題を解く例

問題設定

制約条件の付け方

実行結果（制約条件を変更して比較）

まとめ

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル