
ニューラルネットワークは複雑な非線形関数を近似する事ができるため、回帰問題を解いてみると効果がわかりやすいです。ここではPyTorchのネットワークモデルで色々な非線形関数を回帰してみた結果とそのコードを紹介します。
こんにちは。wat(@watlablog)です。ここではPyTorchを使って非線形関数を回帰していきます!効果がすごいので是非ご覧ください!
本記事の対象者
ニューラルネットワーク初心者
本記事はニューラルネットワーク初心者を対象としています。
当WATLABブログではPyTorchを使ってニューラルネットワークモデルを定義し回帰問題を解いていきますが、まだPyTorchの事がよくわからないという方は是非以下の記事を読んでみて下さい。
まだPyTorchに触れた事がない人でも、順番に読んでいく事できっとこの記事を読み進める事ができるようになるはずです。
PyTorchの概要とインストール
以下の記事でPyTorchの概要とインストールについて説明しています。ここまでの一連の記事で紹介している内容は全てローカルPCで動作させるレベルのものなので、是非お手持ちのPC環境に合わせてPyTorchをインストールしてみて下さい。
PyTorchチュートリアル
PyTorchではテンソル演算を行います。tensor型という聞き慣れない型を使って演算していきますが、使用感はNumpyの行列演算とほぼ同じです。まずは以下の記事でテンソル演算に慣れてみましょう。
「What is PyTorch?」チュートリアルをやってみた
線形ネットワークによる線形回帰とモジュール化
PyTorchのネットワークモデル構築にはひとクセあります。まずは手計算やExcelでもできそうな線形回帰問題(データを直線で近似する問題)を行なって、ネットワークを作って学習するという事がどういう流れなのかを以下の記事で理解しましょう。
PyTorchのネットワークモデルを使って線形回帰をする方法
上記の線形回帰問題ができるようになったら、次はネットワークをモジュール化(クラスで表現してオブジェクト指向で使う)しましょう。ここを理解する事で、他の人が書いたコードが少し読めるようになってくると思います。
以下の記事でPyTorchのネットワークモデルをクラスで書く時のメモをまとめました。
そもそも機械学習やニューラルネットをよく知らない場合
実は機械学習とかニューラルネットワークとかよくわからん。おいしいの?でも非線形回帰はどうしてもしたいの…。
…という方も大丈夫です。僕もその状態から学習を始めており、過去記事に内容を全てまとめていますのでフォロー可能です。
以下のリンクは当ブログの「AI」カテゴリです。リンク先の「G検定」の項目に機械学習、ディープラーニングの分野を体系的にまとめていますので、一通り読む事で本記事の内容にスムーズに繋がると思います。
WATLABブログ:AIカテゴリ
非線形回帰を行いたい人
本記事では特に非線形回帰を行いたい人に向けて書いています。
非線形回帰とは、正弦波や指数関数といった直線で近似できない類の関数に対して回帰分析を行う事です。
Excel等の近似曲線でもフィッティングが難しいような関数を回帰するためには、通常は何かモデル(数式)を定義してから最小二乗法により誤差を最小にするような最適化をかけます。
今回のネットワークモデルを用いた非線形回帰は、全て同じ層構造で学習しますので、モデルを人が定義しないというメリットがあります。
では以下よりニューラルネットワークを用いた非線形回帰コードを説明していきます。
色々な非線形関数を回帰するコード
共通項目の解説
非線形関数を回帰する前に、今回使用するコードの共通項目の解説を行なっていきます。
層/Unitの個数と活性化関数
これまでの線形回帰では、入力層と出力層を直接繋ぐ事が回帰式をそのまま表現する事になっていましたが、それだと直線近似しかできません。
今回は一度線形回帰の式を忘れ、表現力を上げるために中間層を2つ追加してみます。
モデルのコードは以下です。
「PyTorchのネットワークモデルをクラスで書く時のメモ」に対してlinear2, linear3が増えていますが全てnn.Linearで作成しているので、それぞれは線形ネットワークです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 線形回帰ネットワークのclassをnn.Moduleの継承で定義 class Regression(nn.Module): # コンストラクタ(インスタンス生成時の初期化) def __init__(self): super().__init__() self.linear1 = nn.Linear(2, 32) self.linear2 = nn.Linear(32, 16) self.linear3 = nn.Linear(16, 1) # メソッド(ネットワークをシーケンシャルに定義) def forward(self, x): x = nn.functional.relu(self.linear1(x)) x = nn.functional.relu(self.linear2(x)) x = self.linear3(x) return x |
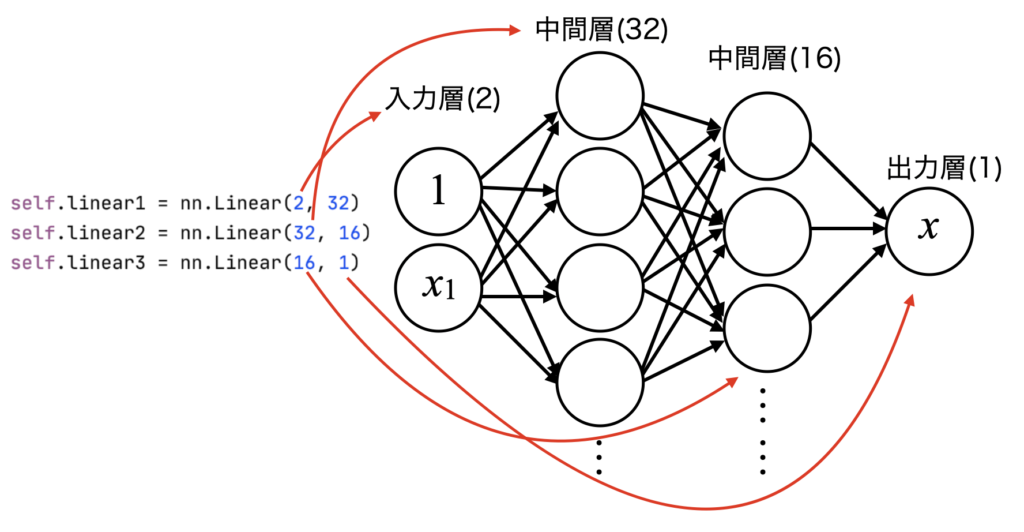
上記linear1〜3の構造を図解したのが下で、nn.Linear(in_features, out_features)に各層における入力Unit数、出力Unit数を設定します。
例えば、横軸時間、縦軸振幅で表現されるデータを回帰する場合、データは線形回帰の時と同じ形だとすると入力層は定数項である1と横軸成分の計2つになります。
そして横軸の成分が与えられた時にただ一つの縦軸値を求めたいので、出力層は1になります。
今回は複雑な非線形関数を近似するため、Unit数32と16の中間層を2層入れています(中間数のUnit数は適当)。
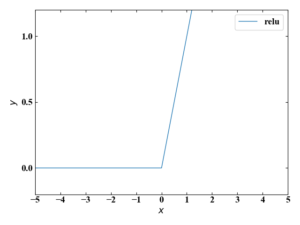
linear1, linear2には活性化関数としてReLUを設定しています。ReLUは下図の関数で、勾配消失問題が発生しにくいためニューラルネットワークの活性化関数に最もよく使われています。
最適化アルゴリズムと損失関数
線形回帰はSGD(確率的降下法)を最適化アルゴリズムに設定していましたが、今回色々試した結果、非線形関数の回帰学習においてはRMSpropが優秀だったので変更しています。
|
1 2 3 |
# 最適化アルゴリズムと損失関数を設定 optimizer = optim.RMSprop(net.parameters(), lr=0.01) # 最適化にRMSpropを設定 E = nn.MSELoss() # 損失関数にMSEを設定 |
RMSpropは勾配降下法の一種ですが、「学習の停滞を改善するRMSPropをPythonで書いてみた」にその他勾配降下法派生種との比較を示していますので、是非ご確認下さい。
正弦波:\(\sin x\)
まずは非線形関数の代表格とも言えるサイン波で回帰してみましょう。
トレーニングデータは以下のコードで生成します。前回と同様に汎用的にNumpyで波形を作り、テンソルへの変換と1ベクトルの追加といったデータ整形を行なっています。
|
1 2 3 4 5 6 |
# トレーニングデータ x = np.random.uniform(0, 10, 100) # x軸をランダムで作成 y = np.random.uniform(0.9, 1.1, 100) * np.sin(2 * np.pi * 0.1 * x) # 正弦波を作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 |
全コード
コピペで動作させる用の全コードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 |
import torch from torch import nn, optim import numpy as np from matplotlib import pyplot as plt # 線形回帰ネットワークのclassをnn.Moduleの継承で定義 class Regression(nn.Module): # コンストラクタ(インスタンス生成時の初期化) def __init__(self): super().__init__() self.linear1 = nn.Linear(2, 32) self.linear2 = nn.Linear(32, 16) self.linear3 = nn.Linear(16, 1) # メソッド(ネットワークをシーケンシャルに定義) def forward(self, x): x = nn.functional.relu(self.linear1(x)) x = nn.functional.relu(self.linear2(x)) x = self.linear3(x) return x # トレーニング関数 def train(model, optimizer, E, iteration, x, y): # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = model(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print('epoch=', i+1, 'loss=', loss) return model, losses def test(model, x): y_pred = model(x).data.numpy().T[0] # 予測 return y_pred # グラフ描画関数 def plot(x, y, x_new, y_pred, losses): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(-5, 15) ax1.set_ylim(-2, 2) ax2.set_xlim(0, 5000) ax2.set_ylim(0.001, 100) ax2.set_yscale('log') # データプロット ax1.scatter(x, y, label='dataset') ax1.plot(x_new, y_pred, color='red', label='PyTorch regression', marker="o", markersize=3) ax2.plot(np.arange(0, len(losses), 1), losses) ax2.text(600, 20, 'Training Error=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 50, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend() fig.tight_layout() plt.show() plt.close() # ------------------------------------------------------------------- # トレーニングデータ x = np.random.uniform(0, 10, 100) # x軸をランダムで作成 y = np.random.uniform(0.9, 1.1, 100) * np.sin(2 * np.pi * 0.1 * x) # 正弦波を作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 # テストデータ x_test = np.linspace(-5, 15, 60) # x軸を作成 x_test = torch.from_numpy(x_test.astype(np.float32)).float() # xをテンソルに変換 X_test = torch.stack([torch.ones(60), x_test], 1) # xに切片用の定数1配列を結合 # ネットワークのインスタンスを生成 net = Regression() # 最適化アルゴリズムと損失関数を設定 optimizer = optim.RMSprop(net.parameters(), lr=0.01) # 最適化にRMSpropを設定 E = nn.MSELoss() # 損失関数にMSEを設定 # トレーニング net, losses = train(model=net, optimizer=optimizer, E=E, iteration=5000, x=X, y=y) # テスト y_pred = test(net, X_test) # グラフ描画 plot(x, y, X_test.data.numpy().T[1], y_pred, losses) |
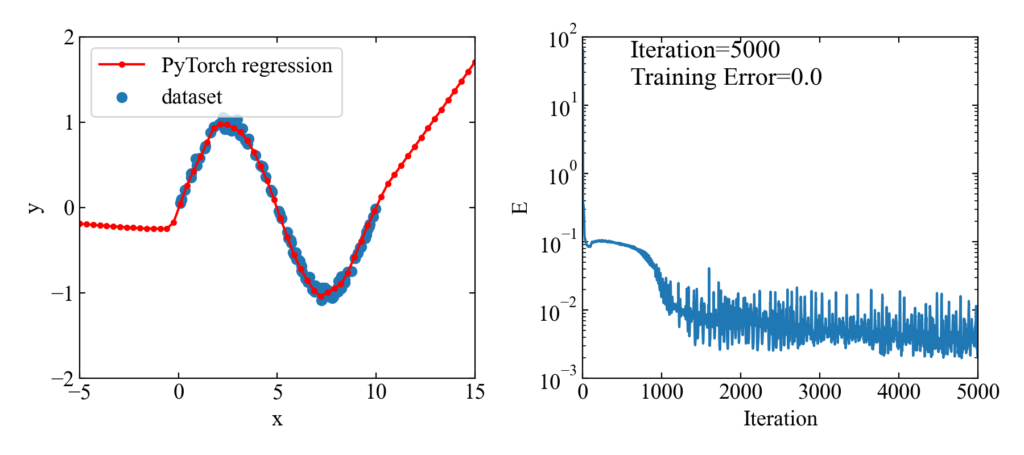
下図が結果です。
5000エポック(エポック=学習回数)とっていましたが、1000あたりでほぼフィッティングされているようです。
トレーニングデータのある範囲においてはよくフィットしていると思います。
全コード(動画生成付き)
以下はおまけです。
学習の過程でどのように回帰されていくかを可視化してみました(面白い!)。
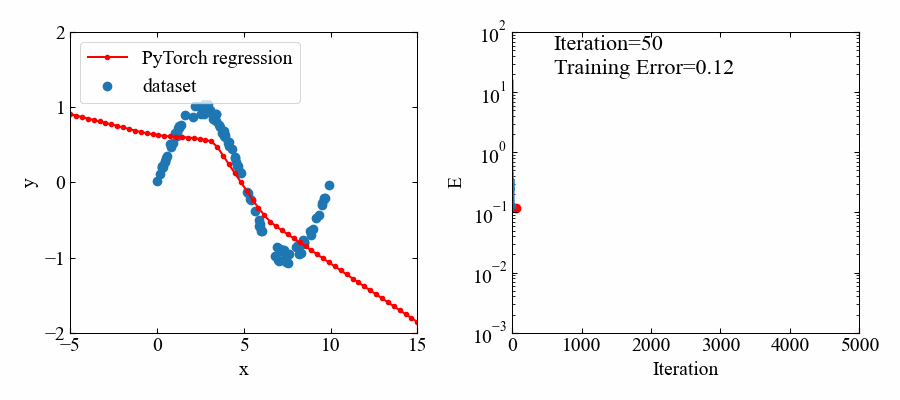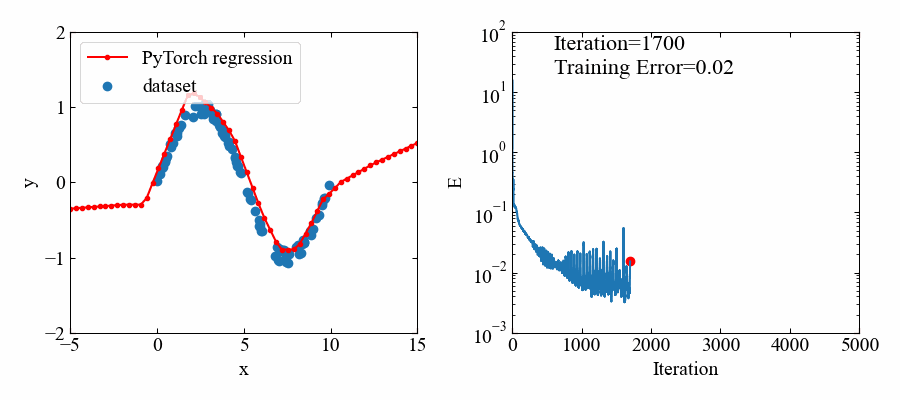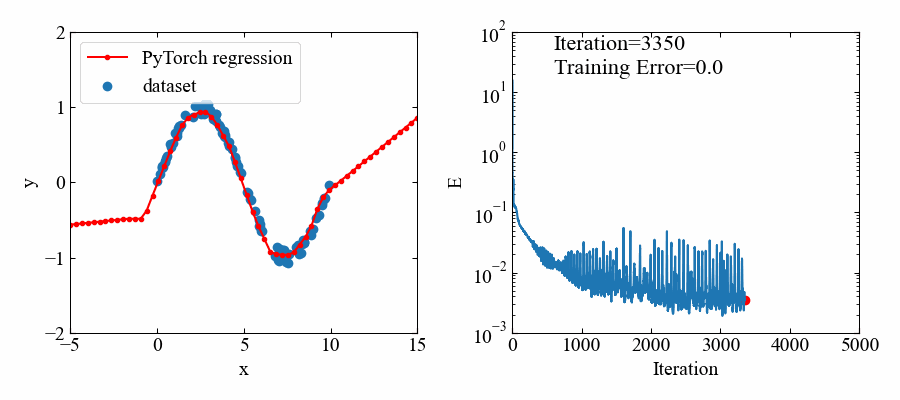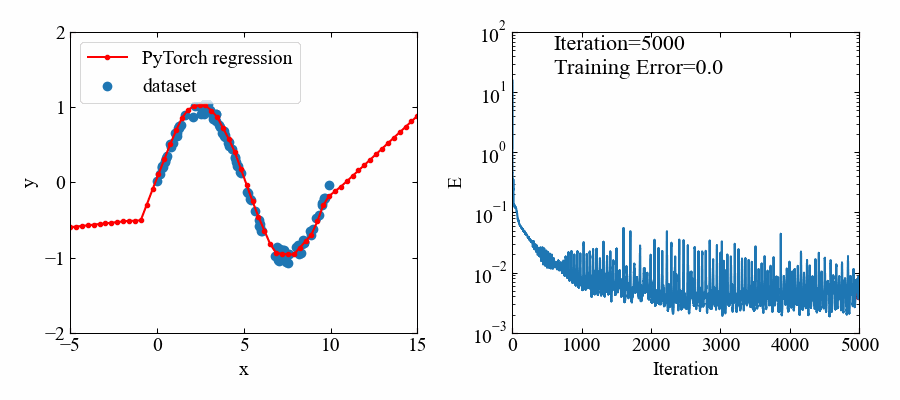
GIF動画生成を行うバージョンのコードを以下に示します。
※こちらは結構コード汚いですので、あくまで参考までに。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 |
import torch from torch import nn, optim import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob # GIFアニメーションを作成 def create_gif(in_dir, out_filename): path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # 線形回帰ネットワークのclassをnn.Moduleの継承で定義 class LinearRegression(nn.Module): # コンストラクタ(インスタンス生成時の初期化) def __init__(self): super().__init__() self.linear1 = nn.Linear(2, 32) self.linear2 = nn.Linear(32, 16) self.linear3 = nn.Linear(16, 1) # メソッド(ネットワークをシーケンシャルに定義) def forward(self, x): x = nn.functional.relu(self.linear1(x)) x = nn.functional.relu(self.linear2(x)) x = self.linear3(x) return x # トレーニング関数 def train(model, optimizer, E, iteration, x, y, X_test, x_plot): # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = model(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print('epoch=', i+1, 'loss=', loss) # 50計算毎にプロットを保存 if (i + 1) % 50 == 0: # グラフ描画 y_test = test(model, X_test) plot(x_plot, y.data.numpy(), X_test.data.numpy().T[1], y_test, losses, 'out', i+1) return model, losses def test(model, x): y_pred = model(x).data.numpy().T[0] # 予測 return y_pred # グラフ描画関数 def plot(x, y, x_new, y_pred, losses, dir, index): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(-5, 15) ax1.set_ylim(-2, 2) ax2.set_xlim(0, 5000) ax2.set_ylim(0.001, 100) ax2.set_yscale('log') # データプロット ax1.scatter(x, y, label='dataset') ax1.plot(x_new, y_pred, color='red', label='PyTorch regression', marker="o", markersize=3) ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses) - 1], color='red') ax2.text(600, 20, 'Training Error=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 50, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend(bbox_to_anchor=(0, 1), loc='upper left') fig.tight_layout() # dirフォルダが無い時に新規作成 if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # plt.show() plt.close() # ------------------------------------------------------------------- # トレーニングデータ x = np.random.uniform(0, 10, 100) # x軸をランダムで作成 y = np.random.uniform(0.9, 1.1, 100) * np.sin(2 * np.pi * 0.1 * x) # 正弦波を作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 # テストデータ x_test = np.linspace(-5, 15, 60) # x軸を作成 x_test = torch.from_numpy(x_test.astype(np.float32)).float() # xをテンソルに変換 X_test = torch.stack([torch.ones(60), x_test], 1) # xに切片用の定数1配列を結合 # ネットワークのインスタンスを生成 net = LinearRegression() # 最適化アルゴリズムと損失関数を設定 optimizer = optim.RMSprop(net.parameters(), lr=0.01) # 最適化にRMSpropを設定 E = nn.MSELoss() # 損失関数にMSEを設定 # トレーニング net, losses = train(model=net, optimizer=optimizer, E=E, iteration=5000, x=X, y=y, X_test=X_test, x_plot=x) # テスト y_pred = test(net, X_test) # グラフ描画 #plot(x, y, X_test.data.numpy().T[1], y_pred, losses, 'out2', 0) # GIFアニメーションを作成する関数を実行する create_gif(in_dir='out', out_filename='pytorch-sinewave-regression.gif') |
正弦波:\(\sin x\)(データを増やした場合)
先ほどはデータ範囲の回帰は十分できていましたが、正弦波がさらに繰り返している場合はどうなるか確かめてみます。
以下のようにxの範囲を-5から15までに拡大したトレーニングデータを使います。
|
1 2 3 4 5 6 |
# トレーニングデータ x = np.random.uniform(-5, 15, 100) # x軸をランダムで作成 y = np.random.uniform(0.9, 1.1, 100) * np.sin(2 * np.pi * 0.1 * x) # 正弦波を作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 |
以下が結果です。やはりデータ範囲がある部分はよく回帰できています(すごい!)。

動画はこちら。
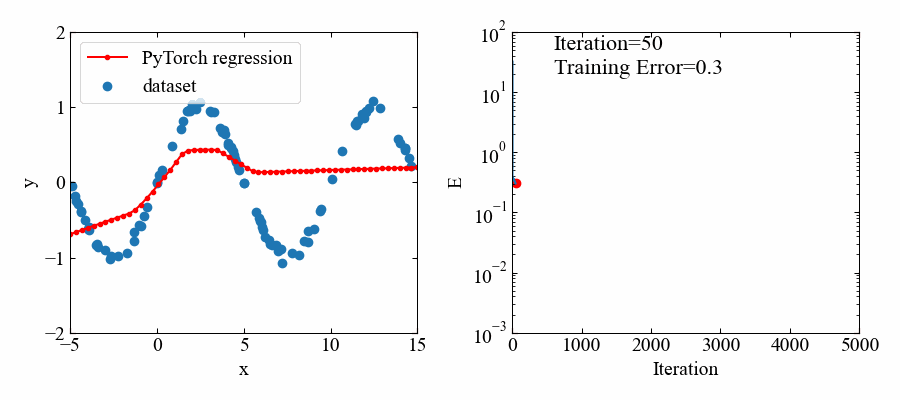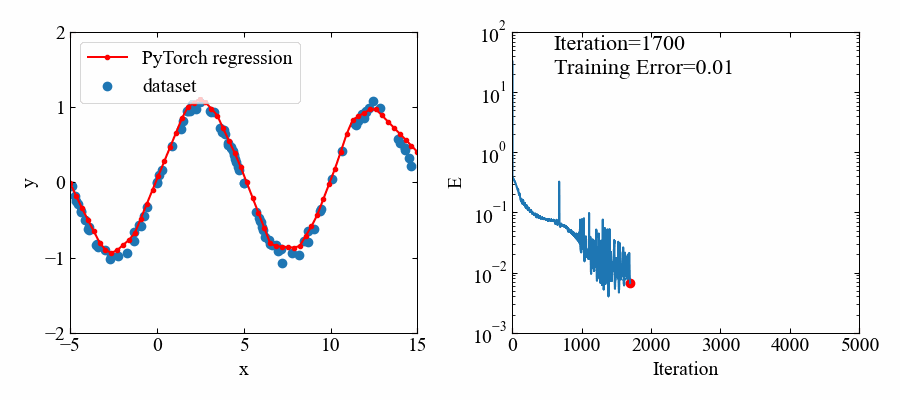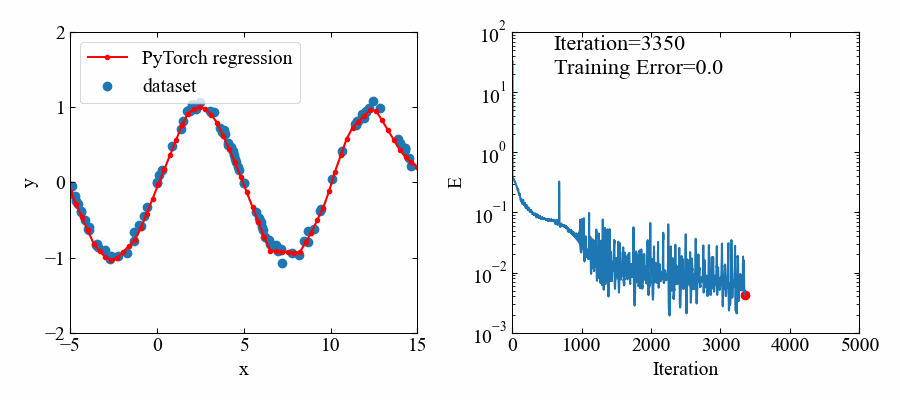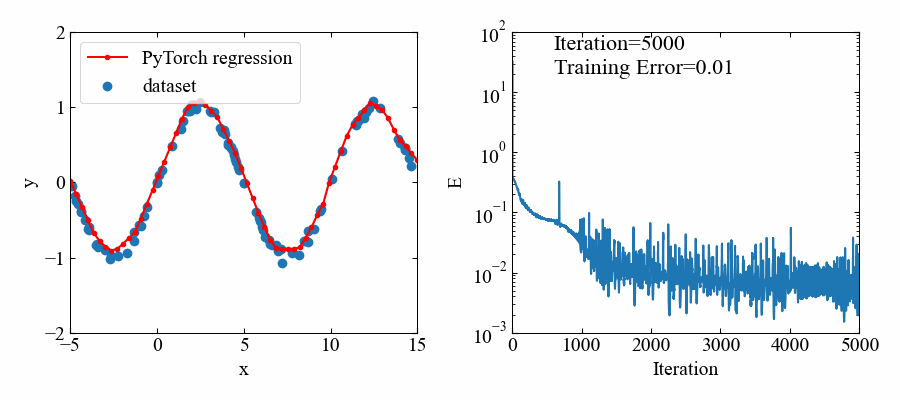
指数関数:\(e^{x}\)
次は指数関数で試してみます。といってもネットワーク構造や最適化アルゴリズムに変化はないので、トレーニングデータを以下にするだけです。
|
1 2 3 4 5 6 |
# トレーニングデータ x = np.random.uniform(0, 10, 500) # x軸をランダムで作成 y = np.random.uniform(0.5, 1.5, 500) * np.exp(x) # 指数関数を作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(500), x], 1) # xに切片用の定数1配列を結合 |
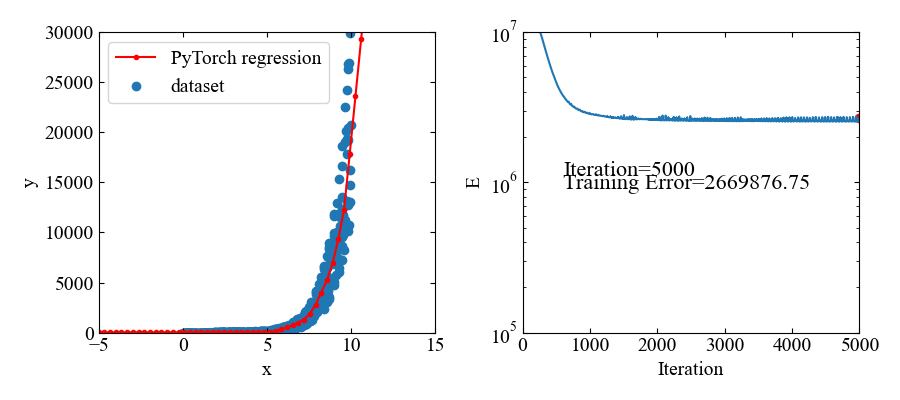
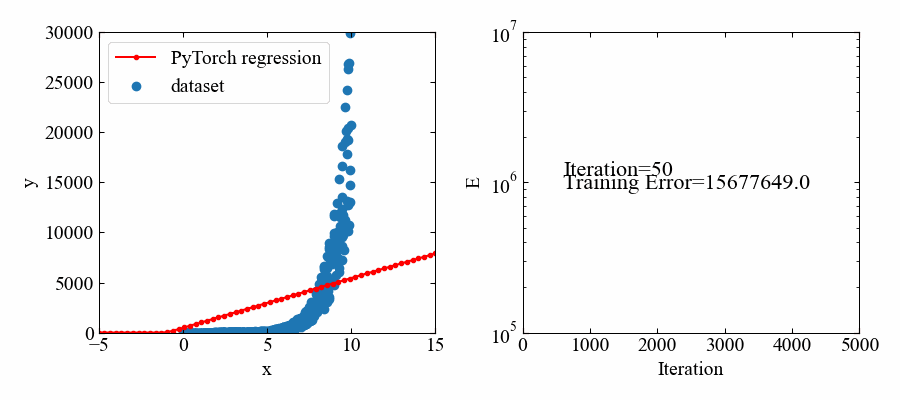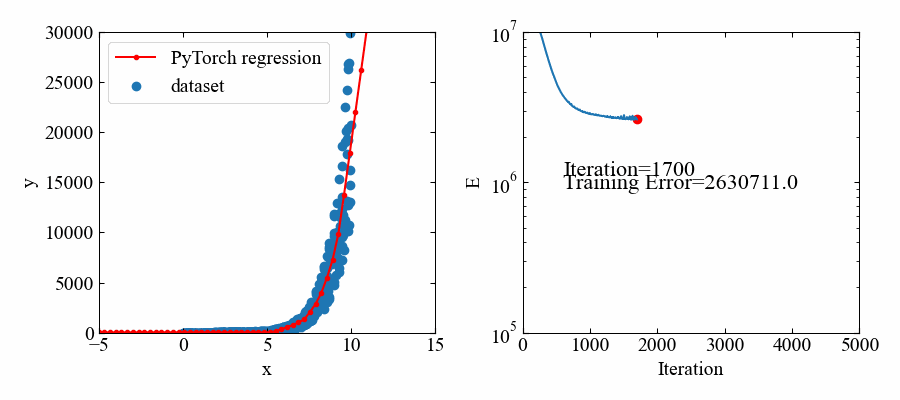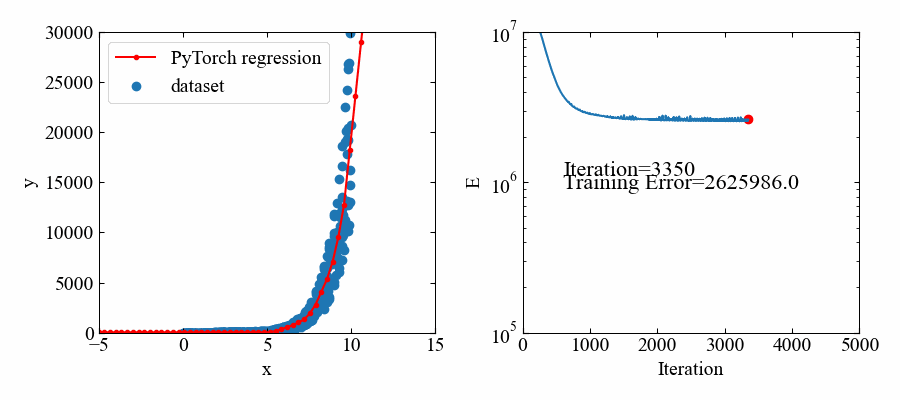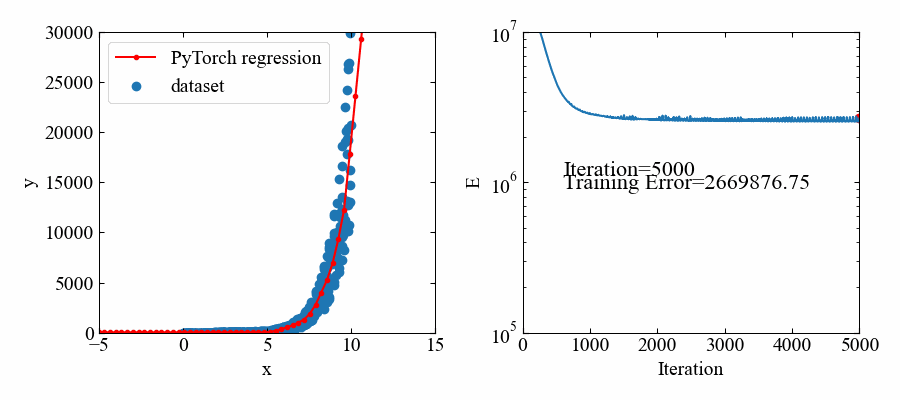
下図が結果です。指数関数であってもフィットできているようです。
但し、値自体が大きいので、損失関数の値も大きな値で推移しています。
動画はこちら。
ハイパボリックタンジェント関数:\(\tanh x\)
ハイパボリックタンジェント関数(\(\tanh x\))も試してみます。
|
1 2 3 4 5 6 |
# トレーニングデータ x = np.random.uniform(-5, 15, 100) # x軸をランダムで作成 y = np.random.uniform(0.9, 1.1, 100) * np.tanh(x) # tanh関数を作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 |
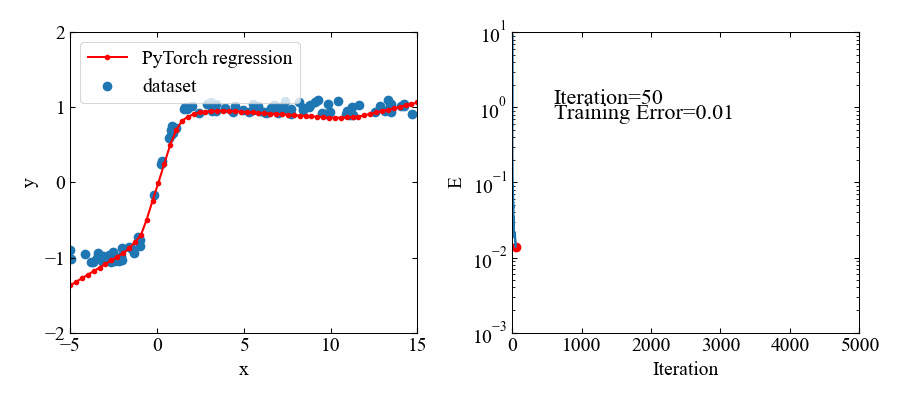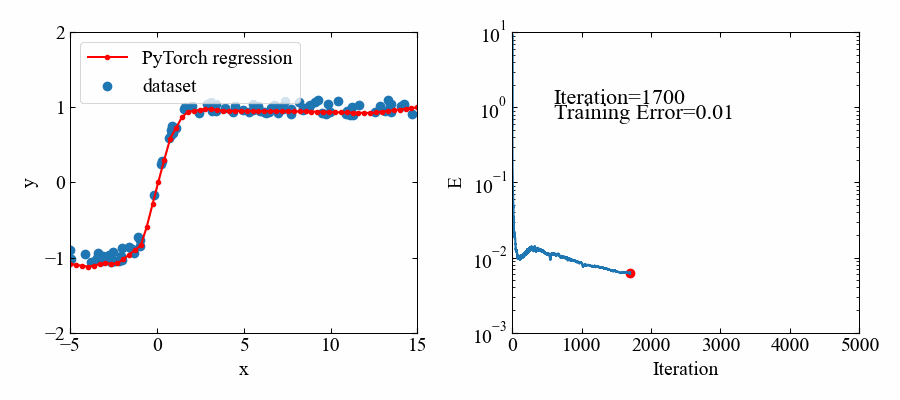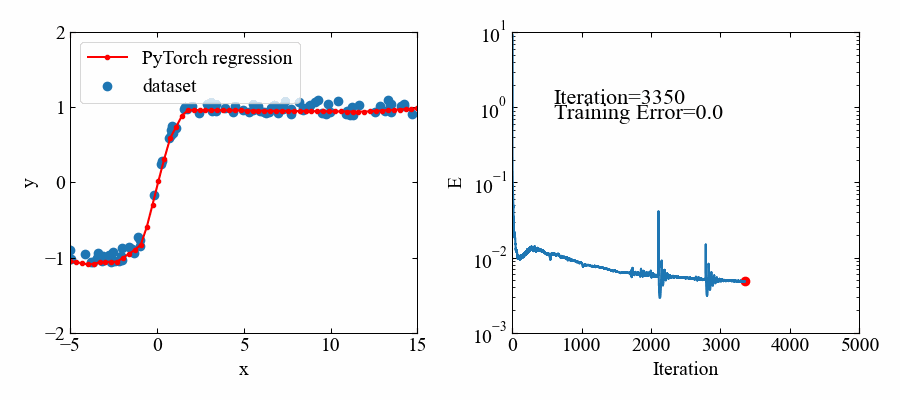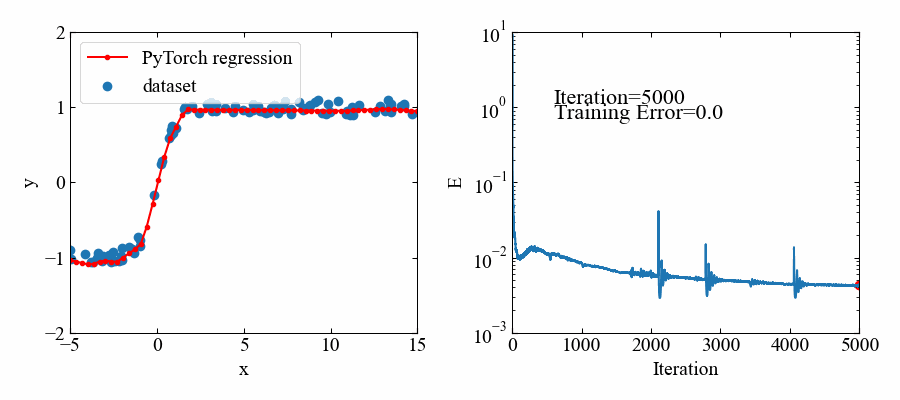
ハイパボリックタンジェントは-1〜1の範囲に値をとりますが、こちらも問題無くフィットできています。
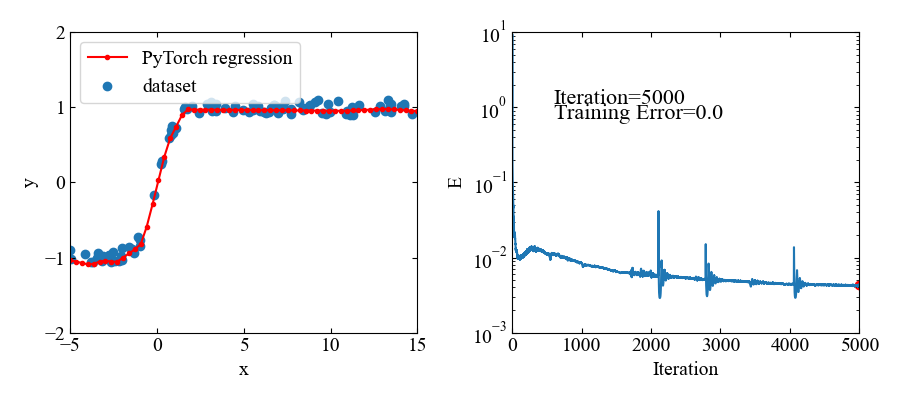
動画はこちら。この関数はすぐ収束しましたね。
非線形関数を回帰するコード(3Dデータセット)
先ほどまでは1つのxに対して1つのyが決まるような関数の回帰でしたが、3Dのデータセットに対しても適用できるか試してみます。
トレーニングデータはこちら。ちょっとコード汚いですが許してください。
|
1 2 3 4 5 6 7 8 9 10 |
# トレーニングデータ x1 = np.random.uniform(0, 10, 30) # ノイズを含んだx軸を作成 x2 = np.random.uniform(0, 10, 30) # ノイズを含んだy軸を作成 grid_x, grid_y = np.meshgrid(x1, x2) # Gridデータを作成 z = np.sin(grid_x.ravel()) * np.cos(grid_y.ravel()) # ノイズを含んだ平面点列データを作成 grid_x = torch.from_numpy(grid_x.ravel().astype(np.float32)).float() # grid_xをテンソルに変換 grid_y = torch.from_numpy(grid_y.ravel().astype(np.float32)).float() # grid_yをテンソルに変換 z = torch.from_numpy(z.astype(np.float32)).float() # zをテンソルに変換 X = torch.stack([torch.ones(len(grid_x)), grid_x, grid_y], 1) # xに切片用の定数1配列を結合 |
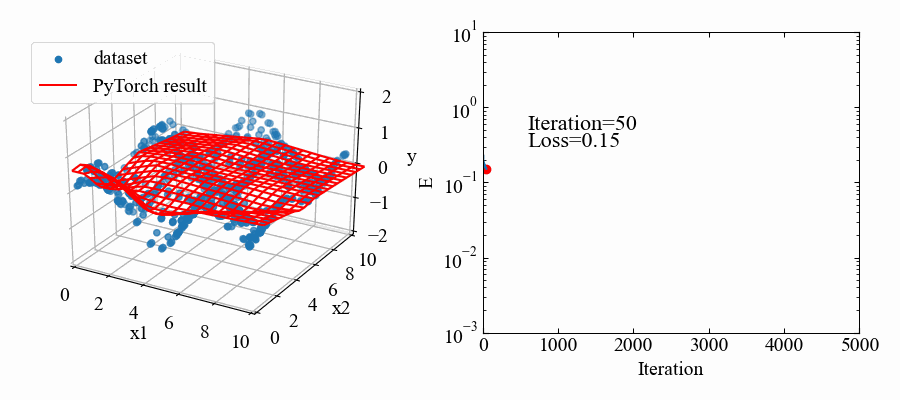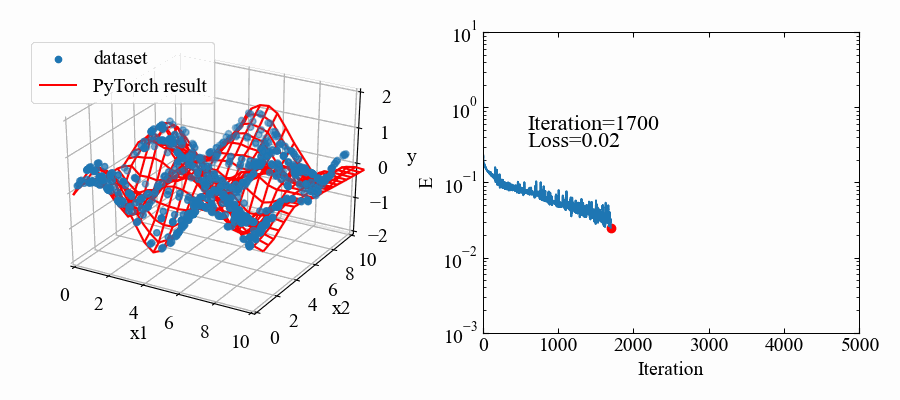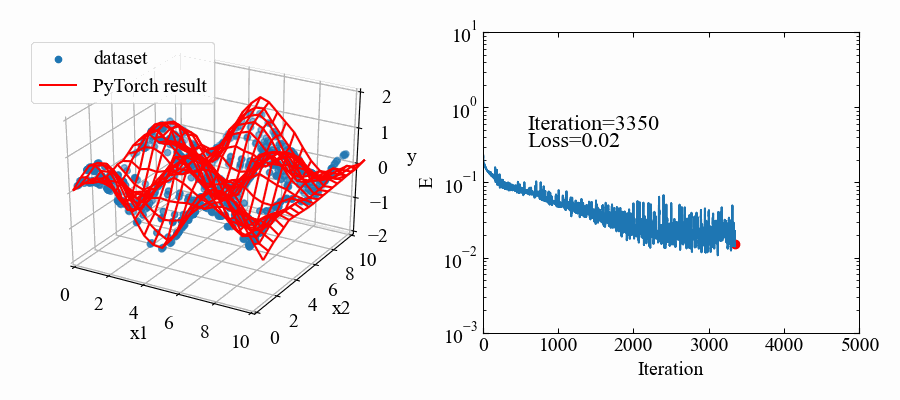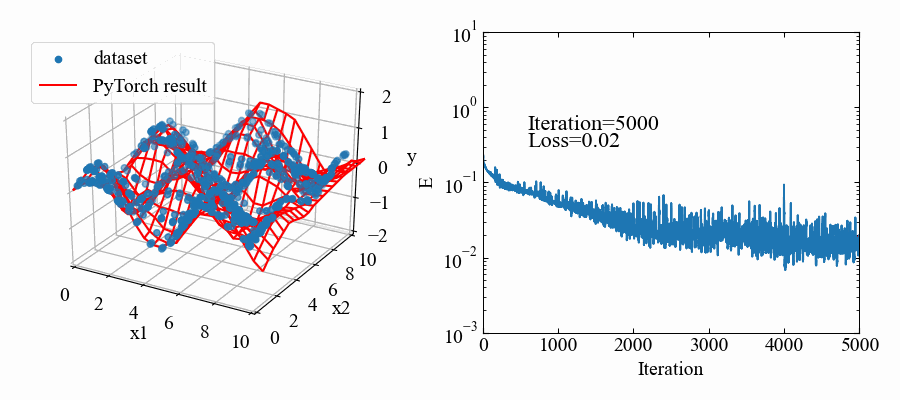
結果はこちら。中間層2個にしては結構良い感じ!

動画はこちら。RMSpropの特徴で解が振動していますが、うねうねと曲面がデータセットに適合していこうとしているのが本当に面白いです!これがやりたかった。
まだ3Dデータセットへの回帰はデータの形合わせに試行錯誤感があってコードはめちゃくちゃ汚いですが、以下に動画作成までの全コードを示します。
3Dデータセットは入力層のin_featuresを3にしているのがポイントです(重回帰分析のテンソルを作った時と同じ)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 |
import torch from torch import nn, optim import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob # GIFアニメーションを作成 def create_gif(in_dir, out_filename): path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # 線形回帰ネットワークのclassをnn.Moduleの継承で定義 class Regression(nn.Module): # コンストラクタ(インスタンス生成時の初期化) def __init__(self): super().__init__() self.linear1 = nn.Linear(3, 32) self.linear2 = nn.Linear(32, 16) self.linear3 = nn.Linear(16, 1) # メソッド(ネットワークをシーケンシャルに定義) def forward(self, x): x = nn.functional.relu(self.linear1(x)) x = nn.functional.relu(self.linear2(x)) x = self.linear3(x) return x # トレーニング関数 def train(model, optimizer, E, iteration, x, y): # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = model(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print('epoch=', i+1, 'loss=', loss) #グラフ描画 X1 = np.arange(0, 11, 0.5) # x軸を作成 X2 = np.arange(0, 11, 0.5) # y軸を作成 X, Y = np.meshgrid(X1, X2) # x軸とy軸からグリッドデータを作成 X2 = torch.from_numpy(X.ravel().astype(np.float32)).float() # xをテンソルに変換 Y2 = torch.from_numpy(Y.ravel().astype(np.float32)).float() # xをテンソルに変換 Input = torch.stack([torch.ones(len(X.ravel())), X2, Y2], 1) # xに切片用の定数1配列を結合 # 50計算毎にプロットを保存 if (i + 1) % 50 == 0: Z = test(model, Input).reshape(X.shape) plot_3d(x.T[1], x.T[2], y, X, Y, Z, losses, 'out', i+1) return model, losses def test(model, x): y_pred = model(x).data.numpy() # 予測 return y_pred # グラフ描画関数 def plot_3d(x1, x2, z, X, Y, Z, losses, dir, index): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(0, 10) ax1.set_ylim(0, 10) ax1.set_zlim(-2, 2) ax2.set_xlim(0, 5000) ax2.set_ylim(0.001, 10) ax2.set_yscale('log') # データプロット ax1.scatter3D(x1, x2, z, label='dataset') ax1.plot_wireframe(X, Y, Z, color='red', label='PyTorch result') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses) - 1], color='red') ax2.text(600, 0.3, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 0.5, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend(bbox_to_anchor=(0, 1), loc='upper left') fig.tight_layout() # dirフォルダが無い時に新規作成 if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # plt.show() plt.close() # ------------------------------------------------------------------- # トレーニングデータ x1 = np.random.uniform(0, 10, 30) # ノイズを含んだx軸を作成 x2 = np.random.uniform(0, 10, 30) # ノイズを含んだy軸を作成 grid_x, grid_y = np.meshgrid(x1, x2) # Gridデータを作成 z = np.sin(grid_x.ravel()) * np.cos(grid_y.ravel()) # ノイズを含んだ平面点列データを作成 grid_x = torch.from_numpy(grid_x.ravel().astype(np.float32)).float() # grid_xをテンソルに変換 grid_y = torch.from_numpy(grid_y.ravel().astype(np.float32)).float() # grid_yをテンソルに変換 z = torch.from_numpy(z.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(len(grid_x)), grid_x, grid_y], 1) # xに切片用の定数1配列を結合 # ネットワークのインスタンスを生成 net = Regression() # 最適化アルゴリズムと損失関数を設定 optimizer = optim.RMSprop(net.parameters(), lr=0.01) # 最適化にRMSpropを設定 E = nn.MSELoss() # 損失関数にMSEを設定 # トレーニング net, losses = train(model=net, optimizer=optimizer, E=E, iteration=5000, x=X, y=z) # GIFアニメーションを作成する関数を実行する create_gif(in_dir='out', out_filename='pytorch-2d-sincos-regression.gif') |
まとめ
同一のネットワークモデルで色々な関数に適応可能な所がすごい
本記事ではニューラルネットワーク初心者の僕が試行錯誤しながら、非線形関数の回帰問題をディープラーニングで解いてみました。
ディープといっても中間層が2層のコンパクトな構造ですが、三角関数や指数関数を始めとした非線形関数を上手い事回帰する事ができました。
また、3Dのデータセットとして\(z=\sin x \cos x\)を用意しましたが、入力層の形だけ揃えた同じ層構造のネットワークモデルで学習する事ができました。
最後にもう一度、観賞用を…。

面白い!
当ブログでは「Pythonサポートベクターマシンで回帰分析!SVRの概要と実装」でも非線形回帰を行なってみました。
しかし、サポートベクターマシンはカーネルがハイパーパラメータであり、精度を出すためにはRBFやpolyといった引数をデータセットに合わせてプログラマが選択する必要がありました。
今回のネットワークモデルは入力時のデータ形式を合わせれば、あとは全く同じ設定で様々な非線形関数を近似できたという事が着目点だと思います。
回帰分析だけでも工学的な問題に色々応用が効きそうですね…。
ディープラーニングのデメリット考察
この界隈の人には普通なのかも知れませんが、僕には驚きの結果でした。
しかしこのネットワークモデル、デメリットは無いのかなと考えてみます。
ディープラーニングによる回帰は確かにすごいですが、例えば物理モデルを数式で定義して回帰問題を解き、その式の係数が意味を持つような研究にはあまり使わない方が良いと感じました。
バックプロパゲーションで自動的に調整された重みは非常に沢山あり、これらの重みから物理的な考察をするのは困難と思うからです。
研究で用いる回帰分析はできるだけ本質を捉えたエッセンシャルモデルで表現する方が良いでしょう。
但し、異音検知等の問題においては物理的な意義よりも判定できるという機能の方が重要なので、ディープラーニングは向いていると思います。
ディープラーニング恐るべし(ミーハー)!非線形回帰はやはり面白いですね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ダイセルイノベーションパークの久保田邦親博士(工学)の材料物理数学再武装ってもの品質工学と化学工学のあいの子みたいで結構面白いよ。
わかりやすい記事をありがとうございます!
少し気になったことがあり、質問させて頂きたいのですが
>>トレーニングデータは以下のコードで生成します。前回と同様に汎用的にNumpyで波形を作り、テンソルへの変換と1ベクトルの追加といったデータ整形を行なっています。
とあるのですが、1ベクトルを追加するのは何のためでしょうか?2021.03.29の記事も拝読して、バイアス項のためかもしれないとは思ったのですが、もしバイアス項を手動で足す必要がある場合、2層目以降でも1を追加してから次の層にインプットする必要が出てくる必要があるのではないかと気になりました。
上記のプログラムをコピーさせて頂き、手元で動かしてみたのですが、学習後にモデルを確認すると
net.linear1.weightのサイズは[32,2]で、net.linear1.biasのサイズは[32]でした。もし入力データに1切片を含めるとすると、net.linear1.weightのサイズは[32,1]になるのではないかと少し気になりました。
自分のpytorchの設定やバージョンなどが違うのかもしれず、また、勉強中のため自分が何か誤解をして読み飛ばしている箇所があったら申し訳ないのですが、もし何かご存じでしたら教えてもらえないでしょうか?
ご訪問ありがとうございます。
1のベクトルを追加しているのは、回帰問題をw0+w1*x1+…という問題に置き換え、
w0は定数項で任意倍しないという意味で1をかけています。
今回のネットワークモデルでは「https://watlab-blog.com/2021/03/29/pytorch-linear-regression/」や
「https://watlab-blog.com/2021/06/13/pytorch-nn-class/」で書いたように、
net = torch.nn.Linear(…bias=False)
とbiasを使わないモデルにしている…はずだったのですが、
この記事にはbiasのパラメータを設定していませんね。。
エラーがなく回帰もできているので特に気づかなかったのですが、どちらでも動いてしまうようです。
もしかしたらtmpさんが気になっているように、少し勘違いしたコードになっているかも知れません。
PyTorch公式のLinearメソッド
「https://pytorch.org/docs/stable/generated/torch.nn.Linear.html」
を読むと、biasはデフォルトがTrueのようです。
「If set to False, the layer will not learn an additive bias.」とあり、この記事のコードはbiasを使わない構想だったので、無駄な学習をしてしまっているかも知れません。
確かにこの部分気になるところですので、もう少し調べた方が良さそうですね。
…実はこちらも見様見真似で書いているのが正直なところです。明確な回答ができず申し訳ございません。。