
信号にノイズが含まれる場合、フィルタ処理をして波形を整形することがあります。フィルタ処理は難しい理論がありますが、PythonのSciPyであれば使うだけなら簡単にできます。
こんにちは。wat(@watlablog)です。
今回はPythonにおけるローパスフィルタの処理について学びます!
ローパスフィルタについて
ローパスフィルタとは?
フィルタとは、日本語で言うと濾過器のことをさします。信号処理の世界では、ある信号から必要な成分のみを抽出する時に使います。
ローパスフィルタ(Low-pass filter)とは、信号の低周波数帯域の成分のみを通過(パス)させ、高周波帯域の成分は阻止(カット)するフィルタのことを指します。
発祥は電気分野とのことですが、電気の世界ではとにかく信号にノイズが乗るような対象を取り扱うので、特に高周波のノイズ成分を除去できるローパスフィルタが多用されています。
ローパスフィルタで重要な因子と用語(図解)
ローパスフィルタは低周波数帯域の信号を通し、高周波帯域の信号を阻止するので、周波数軸で考えると下図のように3つの領域(「通過域」「遷移域」「阻止域」)に分けられます。
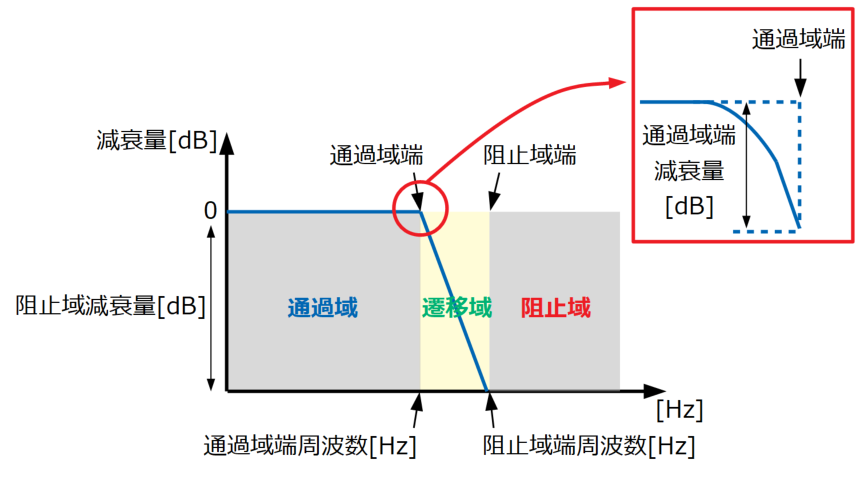
フィルタは通過域の信号はほとんど減衰させないものを指しますが、阻止域で直角に減衰するのではなく、遷移域と呼ばれる徐々に減衰量が変わっていく範囲を持ちます。
さらに、通過域の端部である通過域端周波数でもある程度の減衰量を持ちます。
各周波数でどのような減衰特性を持たせるか、どこまで許容させるのかといった要素を決めて行くのが、フィルタ設計の主目的※です。
※フィルタ処理も元の波形を変化させてしまう信号処理技術であることには変わりがないので、減衰量の設計以外にも信号の位相変化を許容するかどうか、安定性はあるかどうか…といった要素もフィルタ設計にはありますが、今回はそこまで細かい話には踏み込まず、工学の現場でよく使われているバターワースフィルタを扱います。
PythonのSciPyローパスフィルタ
ソースコード
メインファイル
ソースコードを以下に示します。フィルタ処理を実際に行う部分はdef文を使って関数化しました。関数の使い方については「Pythonの関数def文の使い方!引数や別ファイル式も解説」の記事に詳細を示しています。
まずはメイン(main_filter.py)のコードです。
サンプルとしてガウシアンノイズを生成していますが、こちらについては「Pythonでガウス分布を持つノイズの作り方と調整方法」の記事を参照下さい。
中身ですが、上の図で説明した通過域端周波数fp[Hz]と阻止域端周波数fs[Hz]を設定します。またそれぞれの周波数における減衰量もgpassとgstopで設定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import filter_function import numpy as np from matplotlib import pyplot as plt samplerate = 25600 #波形のサンプリングレート x = np.arange(0, 12800) / samplerate #波形生成のための時間軸の作成 data = np.random.normal(loc=0, scale=1, size=len(x)) #ガウシアンノイズを生成 fp = 3000 #通過域端周波数[Hz] fs = 6000 #阻止域端周波数[Hz] gpass = 3 #通過域端最大損失[dB] gstop = 40 #阻止域端最小損失[dB] data_filt = filter_function.lowpass(data, samplerate, fp, fs, gpass, gstop) |
関数ファイル
以下の関数を使ってローパスフィルタを通した波形を取得します。ここで、設定した周波数をナイキスト周波数で除していますが、これはデジタルフィルタを使う時に周波数を正規化する必要があるからです。
以下に引用する公式ページに使い方が書いてあります(日本語検索では意味まで説明していた記事は見当たらず…)。
For digital filters, these are normalized from 0 to 1, where 1 is the Nyquist frequency.
SciPy.org:scipy.signal.buttord
僕はここの正規化の使い方、考え方のエビデンスをとるのに時間がかかってしまいました。初心者の壁かも知れません!
1がナイキスト周波数である必要があるので、サンプリングレートの半分であるナイキスト周波数で割っています。公式ページでは周波数が[Hz]ではありませんが、比をとっているだけなので、設定した周波数とナイキスト周波数がともに[Hz]で書いてあれば問題ありませんね。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np from scipy import signal #バターワースフィルタ(ローパス) def lowpass(x, samplerate, fp, fs, gpass, gstop): fn = samplerate / 2 #ナイキスト周波数 wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化 ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化 N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算 b, a = signal.butter(N, Wn, "low") #フィルタ伝達関数の分子と分母を計算 y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける return y #フィルタ後の信号を返す |
Wnも同様です。正規化する必要があります。そしてこのWnには-3[dB]ポイントという特別な意味合いを持ちます。バターワースフィルタのWn周波数では減衰量が\(1/\sqrt{2}\)(半値、-3[dB])になります。
For a Butterworth filter, this is the point at which the gain drops to 1/sqrt(2) that of the passband (the “-3 dB point”).
SciPy.org:scipy.signal.butter
signal.butterで計算しているbとaは伝達関数の分母分子です。そもそもローパスフィルタを始めとした各種フィルタはラプラス変換を利用して伝達関数の形式で表すことができます。伝達関数の分母と分子はそれぞれ多項式になっているため、このb, aはベクトル形式になっています。
参考:フーリエ変換まで含めた全コード
先ほどまではフィルタ処理の部分のみを解説していましたが、ファイルを2つ作ったり面倒だと思いますので、コピペしてすぐ動かせる全コードを以下に示します。
このコードはサンプル波形を生成して、フーリエ変換とデシベル変換を行っており、フィルタ前後の波形を比較する事が可能です。是非動かして遊んでみて下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
import numpy as np from scipy import signal from scipy import fftpack from matplotlib import pyplot as plt #バターワースフィルタ(ローパス) def lowpass(x, samplerate, fp, fs, gpass, gstop): fn = samplerate / 2 #ナイキスト周波数 wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化 ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化 N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算 b, a = signal.butter(N, Wn, "low") #フィルタ伝達関数の分子と分母を計算 y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける return y #フィルタ後の信号を返す # オーバーラップ処理 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数(平均化に使うデータ個数) array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 return array, N_ave # オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする # 窓関数処理(ハニング窓) def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf # FFT処理 def fft_ave(data_array, samplerate, Fs, N_ave, acf): fft_array = [] for i in range(N_ave): fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))) # FFTをして配列に追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 fft_array = np.array(fft_array) # 型をndarrayに変換 fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis #リニア値からdBへ変換 def db(x, dBref): y = 20 * np.log10(x / dBref) #変換式 return y #dB値を返す # ここからサンプル波形生成とフィルタ処理をする------------------------------------------- samplerate = 25600 x = np.arange(0, 12800) / samplerate # 波形生成のための時間軸の作成 data = np.random.normal(loc=0, scale=1, size=len(x)) # ガウシアンノイズを生成 fp = 3000 # 通過域端周波数[Hz] fs = 6000 # 阻止域端周波数[Hz] gpass = 3 # 通過域端最大損失[dB] gstop = 40 # 阻止域端最小損失[dB] # ローパスをする関数を実行 data_filt = lowpass(data, samplerate, fp, fs, gpass, gstop) # ------------------------------------------------------------------------------ # ここから平均化フーリエ変換とデシベル変換を行う---------------------------------------------- Fs = 4096 # フレームサイズ overlap = 90 # オーバーラップ率 # 作成した関数を実行:オーバーラップ抽出された時間波形配列 t_array_org, N_ave_org = ov(data, samplerate, Fs, overlap) t_array_filt, N_ave_filt = ov(data_filt, samplerate, Fs, overlap) # 作成した関数を実行:ハニング窓関数をかける t_array_org, acf_org = hanning(t_array_org, Fs, N_ave_org) t_array_filt, acf_filt = hanning(t_array_filt, Fs, N_ave_filt) # 作成した関数を実行:FFTをかける fft_array_org, fft_mean_org, fft_axis_org = fft_ave(t_array_org, samplerate, Fs, N_ave_org, acf_org) fft_array_filt, fft_mean_filt, fft_axis_filt = fft_ave(t_array_filt, samplerate, Fs, N_ave_filt, acf_filt) # dB変換する fft_mean_org = db(fft_mean_org, 2e-5) fft_mean_filt = db(fft_mean_filt, 2e-5) # ----------------------------------------------------------------------------------- # ここからグラフ描画--------------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('SP[Pa]') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('SPL[dB]') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, data, label='original', lw=1) ax1.plot(x, data_filt, label='filtered', lw=1) ax2.plot(fft_axis_org, fft_mean_org, label='original', lw=1) ax2.plot(fft_axis_filt, fft_mean_filt, label='filtered', lw=1) plt.legend() # 軸のリミットを設定する。 ax2.set_xlim(0, max(fft_axis_org)/2) ax2.set_ylim(-20, 100) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # ----------------------------------------------------------------------------------- |
実行結果
下図上段が時間波形、下段が上段の波形をFFTした後の周波数波形です。それぞれフィルタ前(original)とフィルタ後(filtered)を比較しています。
ここではFFTやデシベル変換も使っていますが、それぞれの詳細は以下の記事にまとめていますので、是非ご覧ください。
PythonでFFT!SciPyのFFTまとめ
Pythonで音圧のデシベル(dB)変換式と逆変換式
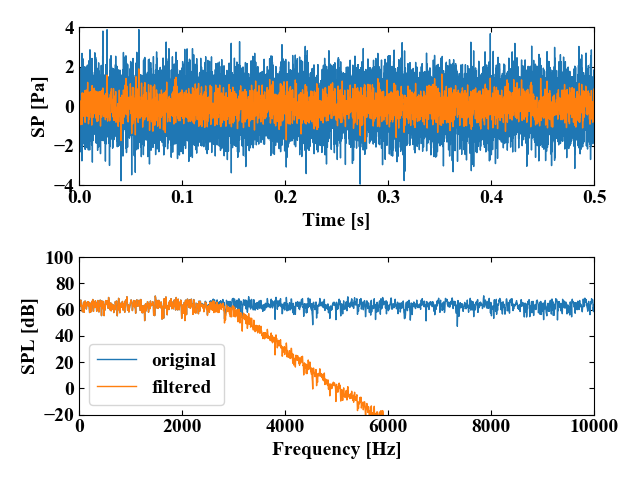
元の時間波形はガウシアンノイズなので周波数全体でフラットな特性を持っていますが、フィルタ後は設定した周波数(fp=3000[Hz])から綺麗に減衰していく結果を得ました。
ノイズ波形だけではつまらないので、サイン波のノイズ除去を行ってみましょう。上のメインコード(main_filter.py)の波形生成部分とフィルタ周波数を以下のように変更してみます。
|
1 2 3 4 5 6 7 8 |
samplerate = 25600 x = np.arange(0, 12800) / samplerate # 波形生成のための間軸の作成 data = np.sin(2.0 * np.pi * 50 * x) + 0.3 * np.random.normal(loc=0, scale=1, size=len(x)) #サイン波にガウシアンノイズを重畳 fp = 200 #通過域端周波数[Hz] fs = 400 #阻止域端周波数[Hz] gpass = 3 #通過域端最大損失[dB] gstop = 40 #阻止域端最小損失[dB] |
すると元の時間波形はノイジーなサイン波、フィルタ後はノイズが軽減している結果を得ます。このページでは極端な例を紹介していますが、これがフィルタ処理の効果です。
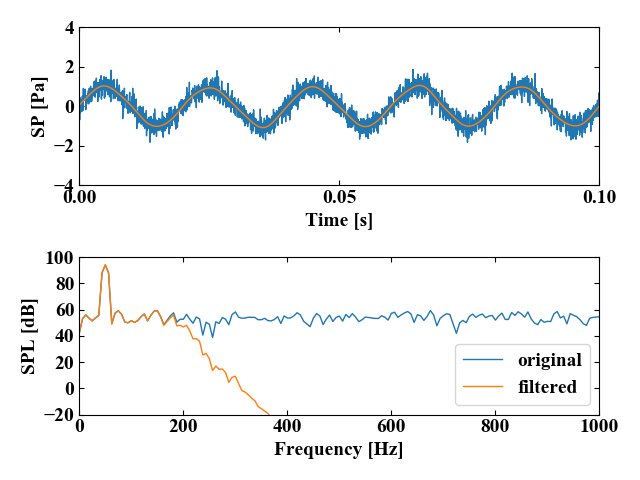
ソースコードの周波数や減衰量を変えると、減衰が始まる位置、遷移域の傾きを自在に変化させることができますので、是非トライしてみて下さい。
まとめ
フィルタ処理の一種であるローパスフィルタをPythonで使えるようになりました。
ローパスフィルタは周波数軸で通過域、遷移域、阻止域における周波数と減衰量を決める必要があります。
フィルタをかける時に使用する伝達関数の入力値はSciPyの関数を使うことで簡単に求めることができました。
理解するのに時間はかかったけど、ようやくフィルタ処理ができるようになってきたぞ!ここから各種フィルタに発展させていこう!
また、英語の公式ページを見ると理解が深まることがわかったので、これからは積極的に海外Webページも活用していこう!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
いつも参考にさせていただいています。
時系列データの全体に載っているノイズを除去したく、ローパスフィルターの上記コードを利用しているのですが、gstopの値の設定方法がよくわかりません。
①まずFFTによって周波数データに変換し、縦軸の振幅値をdB変換するのですが、0Hzにおける振幅値をA0として、dB値は20*log10(A/A0)で計算は合っていますでしょうか?
②gstopの値はどのようにして設定するのが妥当でしょうか?
バタワースフィルターでは減衰傾度がある以上、一定周波数以上のデータを完全にカットする、というのは難しいのですが、何とかきれいにノイズ除去できる方法がないかと模索中です。。
よろしくお願いします。
いつもありがとうございます。
gpassとgstopの使い方は、まずは正式に1次情報である以下の公式サイトをご参照ください。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.buttord.html
この記事の図の「通過域端減衰量」がgpassで、「阻止域端減衰量」がgstopとなります。
0[Hz]における振幅値は関係なく、単純に「信号をどれだけ減衰させたいか」で設定します。
ただ、仰るとおりの理由で完全にノイズをカットすることは難しいです。
完全に周波数でノイズをカットする1手法として、フーリエ変換して関連帯域を0にしてから(複素数のフーリエスペクトル、負の周波数帯域も0にする)逆フーリエ変換することが考えられます。
但し、フーリエ変換を使う方法はある程度の区間を平均化するため、時間軸で変動のある信号に対しては万能ではありません。
フィルタを綺麗にかけるというのは「フィルタ設計」と呼ばれるほど奥が深い分野ですので、より専門的にはこのキーワードで勉強する必要があると思います。
ざっとGoogle検索するとやはりこの通過域端、阻止域端の工夫が研究されているようです。
(僕はこの分野のプロではないので、この領域はまだ未熟。。。あまり深い回答はできず申し訳ないです。このページに疑問を投げかけることで、もしかしたらプロから回答があるかも…?)
是非色々調べてください。ただ不明点があればこちらも勉強できるので、気軽にお声がけください!