ディープラーニングのフレームワークであるPyTorchを学ぶために、まずは超簡単な線形回帰問題を解いてみます。ここではtorchのネットワーク構築方法、最適化モデル選択、損失関数の設置方法と基礎的な使い方を紹介します。
こんにちは。wat(@watlablog)です。ここではPyTorchで線形回帰問題を解く事で、ディープラーニングフレームワークの基本的な使い方を学びます!
前半は動作環境、PyTorchや線形回帰の概要について少々おさらいを書いていますので、いきなりコードを見たい方は目次で飛んでみて下さい!
動作環境
通常ディープラーニングを使用する時は重い計算をするため、Google Colabratory等でGPUを活用した計算を行います。しかし、ここではPyTorchの使い方を理解する事を主目的にしているため、軽い計算を手持ちのPCで実行しますので、今回確認した動作環境をメモしておきます。
| PC | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] | |
| Python | Python 3.7.7 | |
| PyTorch | torch==1.5.1 | |
PyTorch導入と動作確認
PyTorchの概要とインストール方法
PyTorchはTensorFlow, Keras, Chainer...といった数ある深層学習(ディープラーニング)フレームワークの一つです。自分でゼロから作らなくてもネットワークを生成したり、最適化を行ったりする事が可能です。
人によって好き嫌いがあったり、使いやすい物は違うと思いますが、PyTorchはちょっと前から注目されています。僕がPyTorchに決めた理由はインストール方法と共に以下の記事に記載していますので是非ご覧下さい。
「ディープラーニング初心者がPyTorchを選んだ3つの理由」
チュートリアルで動作確認
PyTorchをインストールした後はまずはチュートリアルをやって動作確認をしましょう。PyTorchの基本はテンソル演算です。詳しくは以下の記事に記載しました。
「「What is PyTorch?」チュートリアルをやってみた」
線形回帰のおさらい
線形回帰とは?
線形回帰(Linear regression)とは、ある従属変数の値を別の説明変数(独立変数)によって予測する事です。
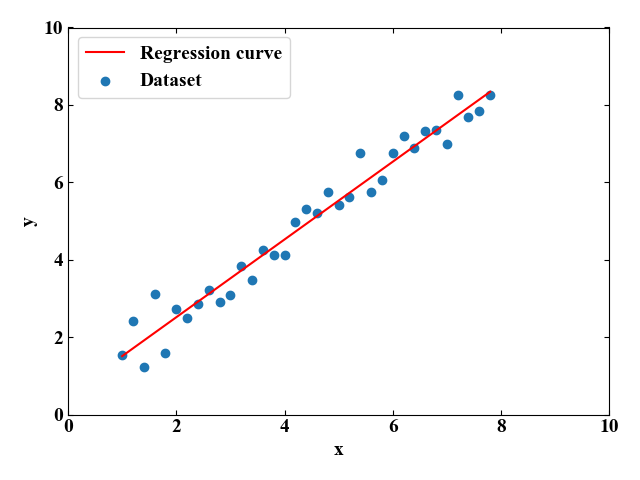
例えば、任意のデータセットが与えられ、説明変数\(x\)1つから従属変数\(y\)の値を予測する場合、以下のように各データ点との誤差を最小にするように1本の直線を引く事が出来ます。
説明変数が複数ある時も同様です。以下は2つの説明変数を使った場合です。先ほどのように説明変数が1つだけの場合は単回帰、以下のように説明変数が2つ以上の場合は重回帰と呼ばれます。
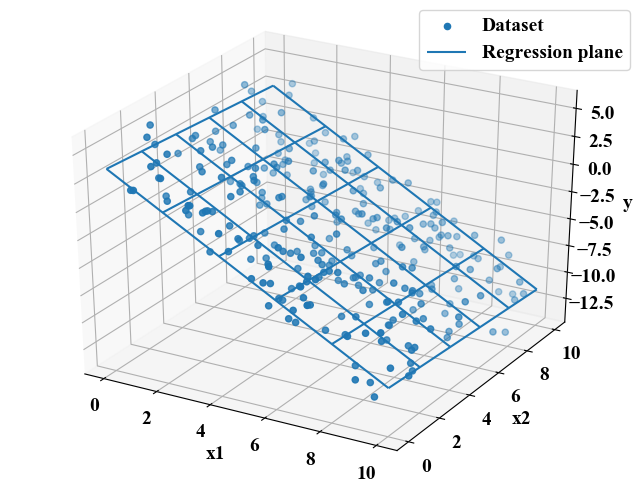
2つの説明変数の場合は上図のように回帰平面が得られますが、3つ以上の場合は図で表す事が不可能な超平面になります。ただし、どれだけ変数の数が増えても線形回帰の場合は超平面がぐにゃぐにゃと曲がる事はありません。
線形回帰を行う色々な方法
当WATLABブログでは、線形回帰を題材に複数のコードを書きました。ここでは参考までに線形回帰を行う色々な方法(PyTorch以外の方法)をご紹介します。
Numpyを使う方法
最小二乗法としてスクラッチしたコードや、Numpyのpolyfitを使っても単回帰は簡単にできます。特に軽い用途でちょっと実験データにフィットさせた線が欲しい時はNumpyで十分でしょう。
「Pythonでカーブフィット!最小二乗法で直線近似する方法」
scikit-learnを使う方法
scikit-learnは古典的な機械学習モデルが詰まったお得なライブラリです。単回帰、重回帰程度であればこちらでも十分です。
「Python機械学習!scikit-learnによる単回帰分析」
「Python機械学習!scikit-learnによる重回帰分析」
このように別にPyTorchを使わなくても線形回帰は簡単にできますが、今回はPyTorchの基礎を学ぶためにネットワークによる回帰分析を行います。
線形回帰の式
基礎知識として線形回帰の式を知っておく必要があります。
線形回帰は\(n\)個の説明変数\(x_{i}\)にそれぞれ重み\(w_{i}\)がかかった線形結合の形で表現可能です(式(1))。専門的には最後に擾乱項という誤差項\(\epsilon\)がつきますが、ここでは省略します。
式(1)はシグマを使って式(2)と書く事もでき、この方がシンプルになります。
さらに、式(2)のシグマ内はベクトルの内積の形で書くと\(\mathbf{w}^{\mathsf{T}} \mathbf{x} \)となりますが、ベクトル\(\mathbf{x} =[1, x_{1}, x_{2}, \cdots, x_{n}]\)と1を最初に入れる事で式(3)のようにさらにコンパクトな形にする事が可能です。
次に、この線形回帰をネットワークで表現してみます。
線形回帰のネットワークモデル
PyTorchのようなディープラーニングのフレームワークはネットワークモデルを作って重みパラメータを学習していきます。そのため、線形回帰もネットワークモデルとして考える必要があります。
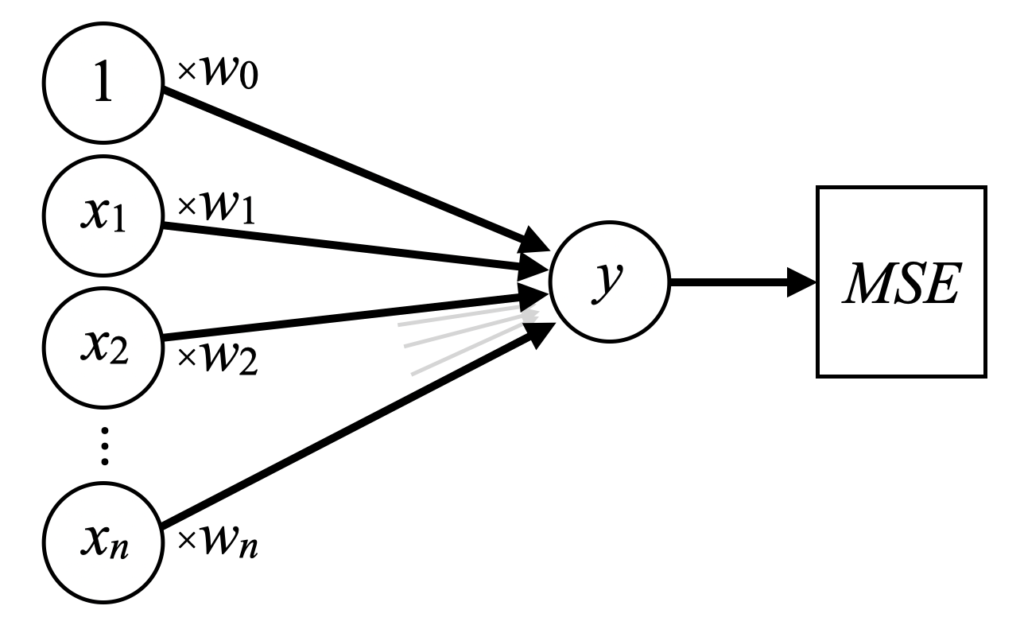
式(3)の線形回帰式をネットワークモデルで表現した図を下に示します。入力層と出力層の2層から構成された単純なネットワークが重回帰のネットワークモデルとなります。
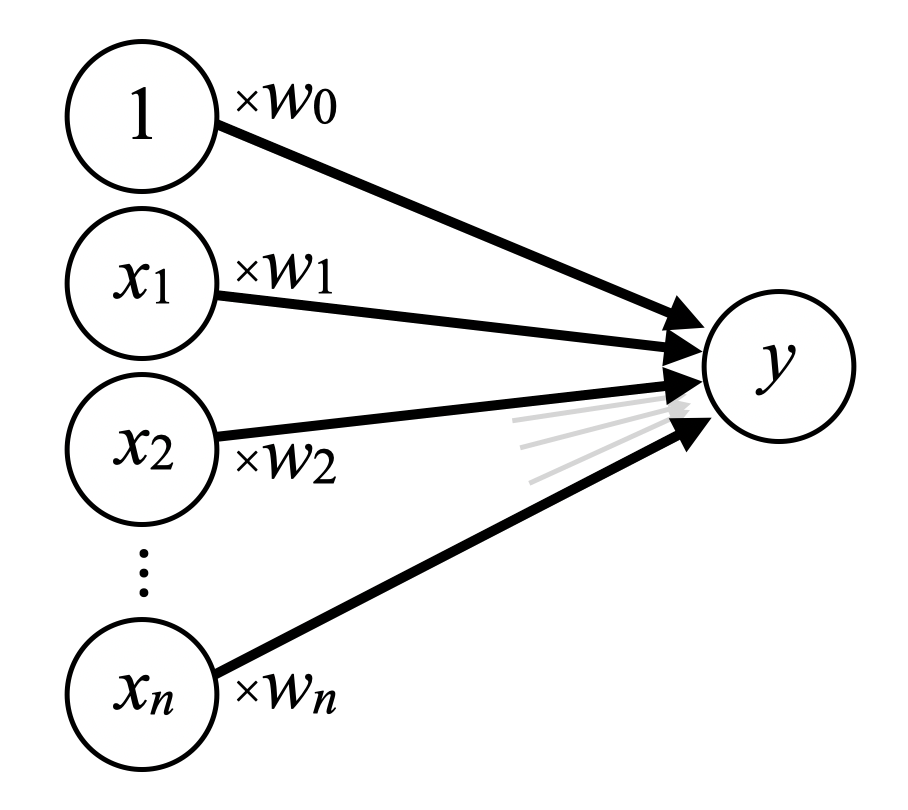
上記ネットワークは全然ディープではありません。ここに中間層を沢山追加したり、活性化関数を追加したりする事でディープニューラルネットワークとなっていき、もはや線形ではなく複雑なモデルを作り上げる事ができるネットワークが出来上がります(当面の目標です)。
ディープラーニングでどんな事をやっているかは、G検定を勉強した時に作った「【G検定の学習】ディープラーニングの概要と具体的な手法」という記事が参考になると思います。ネットワークモデルとは?学習はどう進む?バックプロパゲーション?…と気になった方は是非ご覧下さい。
損失関数
平均二乗誤差MSE
ネットワークモデルを用いて予測した値は学習を繰り返さないとうまく回帰できません。逐次計算を行いながら、正解と比べてどのくらい誤差があるか、損失関数を設定して評価する必要があります。
回帰問題の場合、平均二乗誤差(MSE:Mean Squared Error)がよく使われます。
MSEは式(4)で表し、正解値\(y\)と予測値\(\hat{y}\)との差の二乗を平均化します。最小二乗法でも使われるのでおなじみですね。「\(\hat{}\)」はハットと呼びます。
最適化手法
確率的勾配降下法SGD
続いて勾配降下法(GD:Gradient Descent)の知識も必要です。ネットワークモデルを構築し、損失関数\(E\)を用いて評価値を計算した後は、さらに損失関数\(E\)を小さくする最適な重み\(\mathbf{w}\)を探索します。
関数の偏微分(ここでは重み\(\mathbf{w}\)の偏微分)から勾配情報を取得し、勾配を降る方向に重みを調整していく事が勾配降下法でやっている事です。
式(5)が勾配降下法の基礎式です。全重みに対して偏微分を求めるのが元の理論ですが、ディープラーニングのように膨大な数の重みがある場合は計算コストの低減のために、ランダムに一部の値のみを使う確率的勾配降下法(SGD:Stochastic Gradient Descent)を選択する場合も多いです。
\(\eta\)は学習率で、勾配降下法のハイパーパラメータ(事前に決めておく必要のあるもの)です。学習率\(\eta\)は大きさによって学習の収束性に大きく影響します。詳しくは「Pythonで1変数と2変数関数の勾配降下法を実装してみた」に学習率の影響も含めてまとめましたので、参考にして下さい。
今回はPyTorchで勾配降下法を実装しますが、Numpyによる勾配降下法を使った線形回帰コードは以下の記事をご覧下さい。
「勾配降下法を回帰分析に適用する式と実装のためのPythonコード」
また、当ブログの「AIカテゴリ」にはその他改良版の勾配降下法もNumpyで書いたコードがありますので、そちらも是非参考にして下さい。
PyTorchによる単回帰分析のコード
出力
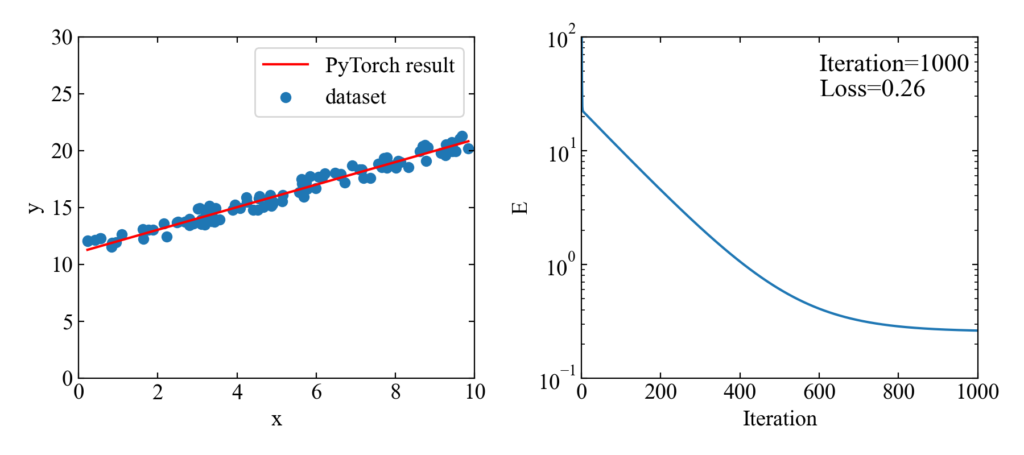
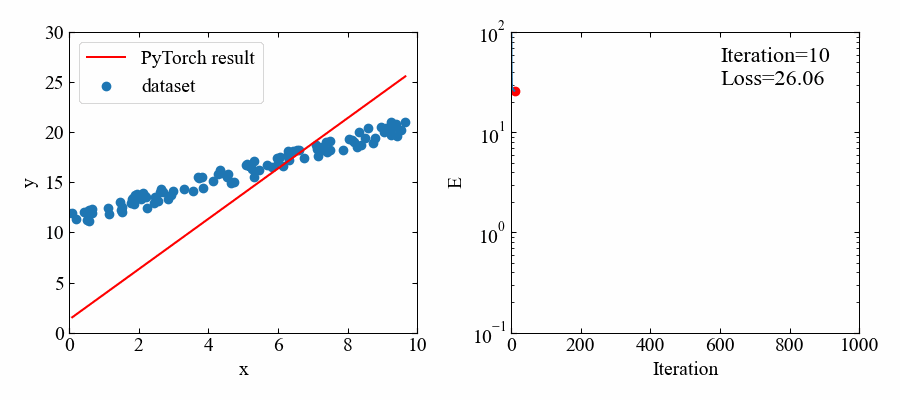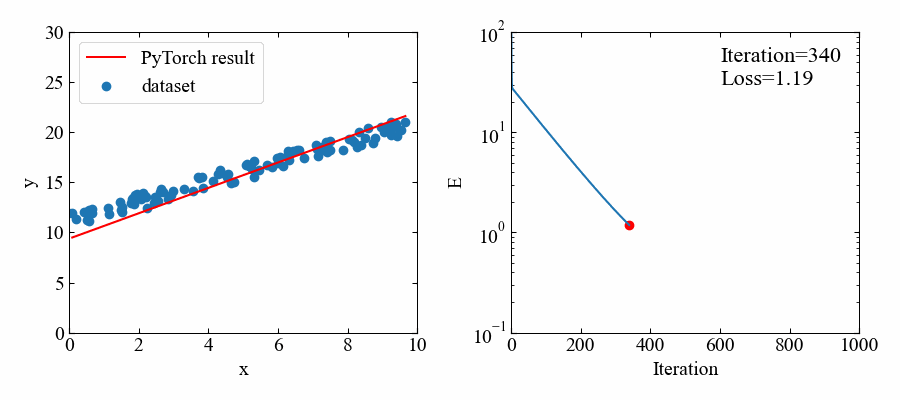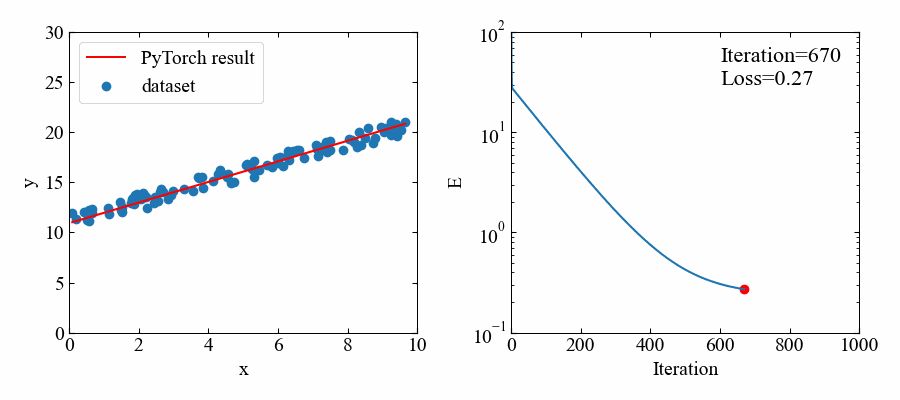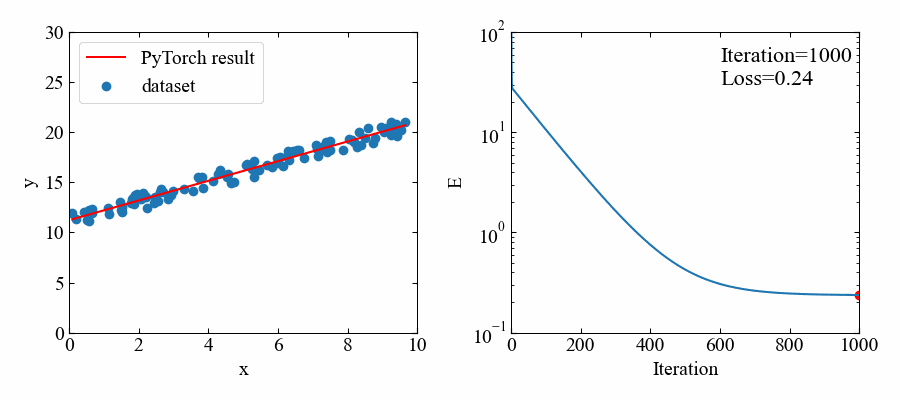
ここで紹介するコードは下図のように、データセットに対する回帰直線の結果(左)と、イタレーションと損失関数の評価値(右)を出力します。
全コード
詳細説明する前に、貼り付けてすぐに動かせる全コードを紹介します。
サンプルデータをNumpyで生成して、PyTorchで扱えるTensor型に変換、linear_regression関数を実行し、matplotlibで結果を見る、という内容です。
linear_regression関数実行時には特徴量の数dimensionと反復計算数iteration、学習率lr、データx, yを与えます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
import torch import numpy as np from matplotlib import pyplot as plt def linear_regression(dimension, iteration, lr, x, y): net = torch.nn.Linear(in_features=dimension, out_features=1, bias=False) # ネットワークに線形結合モデルを設定 optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 最適化にSGDを設定 E = torch.nn.MSELoss() # 損失関数にMSEを設定 # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = net(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print(list(net.parameters())) # 回帰係数を取得して回帰直線を作成 w0 = net.weight.data.numpy()[0, 0] w1 = net.weight.data.numpy()[0, 1] x_new = np.linspace(np.min(x.T[1].data.numpy()), np.max(x.T[1].data.numpy()), len(x)) y_curve = w0 + w1 * x_new # グラフ描画 plot(x.T[1], y, x_new, y_curve, losses) return net, losses def plot(x, y, x_new, y_pred, losses): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(0, 10) ax1.set_ylim(0, 30) ax2.set_xlim(0, 1000) ax2.set_ylim(0.1, 100) ax2.set_yscale('log') # データプロット ax1.scatter(x, y, label='dataset') ax1.plot(x_new, y_pred, color='red', label='PyTorch result') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.text(600, 30, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 50, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend() fig.tight_layout() plt.show() plt.close() # ------------------------------------------------------------------- # サンプルデータ x = np.random.uniform(0, 10, 100) # x軸をランダムで作成 y = np.random.uniform(0.2, 1.9, 100) + x + 10 # yを分散した線形データとして作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 # 線形回帰を実行 net, losses = linear_regression(dimension=2, iteration=1000, lr=0.01, x=X, y=y) |
実用的にはclassで書いた方が良いと思いますが、ここでは初心者が慣れ親しんでいると考えられるdef関数にしてみました(僕もまだclassを見ると若干のアレルギー反応が見られますので…)。
詳細コード説明
サンプルデータを生成しTensor型にする
PyTorchによるネットワークモデルの演算はテンソルで行われます。そのため、データはTensor型に変換する必要があります。
サンプルコードなので、初めからTensorで書いても良かったのですが、実際に分析したいデータが初めからTensorになっている事はほとんど無いという事を考慮し、あえてPythonでは汎用的なNumpyでデータセット生成を行っています。
データ生成とTensorへの変換は以下のコードで行います。基本は.from_numpy()でTensor型に変換されるのですが、最後に.float()が無いと「RuntimeError: Expected object of scalar type float but got scalar type double for sequence element 1.」と途中でエラー終了します。
|
1 2 3 4 |
x = np.random.uniform(0, 10, 100) # x軸をランダムで作成 y = np.random.uniform(0.2, 1.9, 100) + x + 10 # yを分散した線形データとして作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 |
切片項を入力に含める加工
先ほどのデータセットそのままだとネットワークにバイアス項を設定したりする必要が出てきますが、切片も入力に含める事で重みとして一括で学習させる事が出来ます。そのための加工方法を紹介します。
…何を言っているかわからないと思いますが、僕も初めは何をしているのかわかりませんでした。
以下の参考書を読んでなんとなく理解はできましたが、イマイチ迷った所があるので、図で説明します。
図にすれば簡単ですので、是非上記書籍の補助として参考にして下さい。
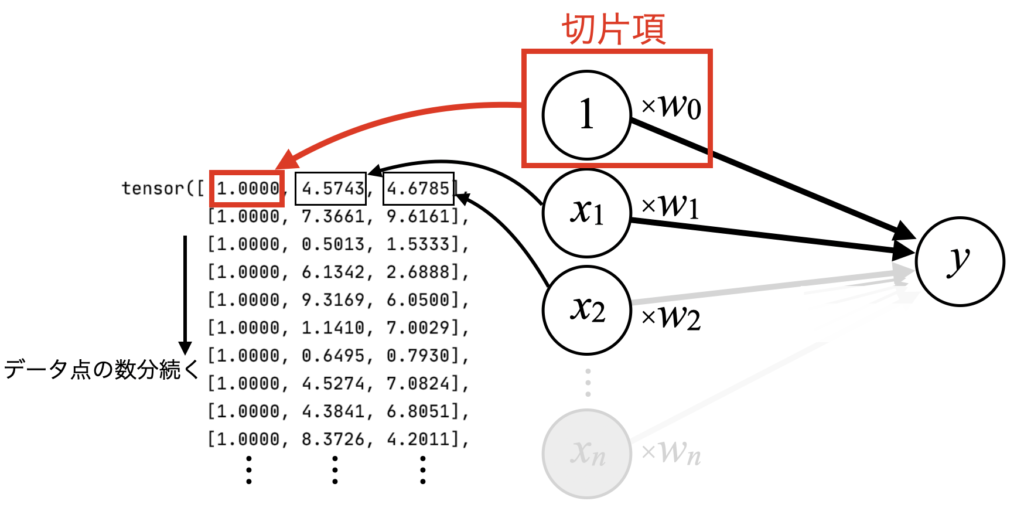
上で説明していた回帰分析のモデルで、最初の項を切片項として組み込むという事は、下図のtensor()の形にデータセットを加工する必要があります。
データセットは複数の点から構成されますが、それぞれが[1, \(x_{1}\)]になっている必要があるという意味です。
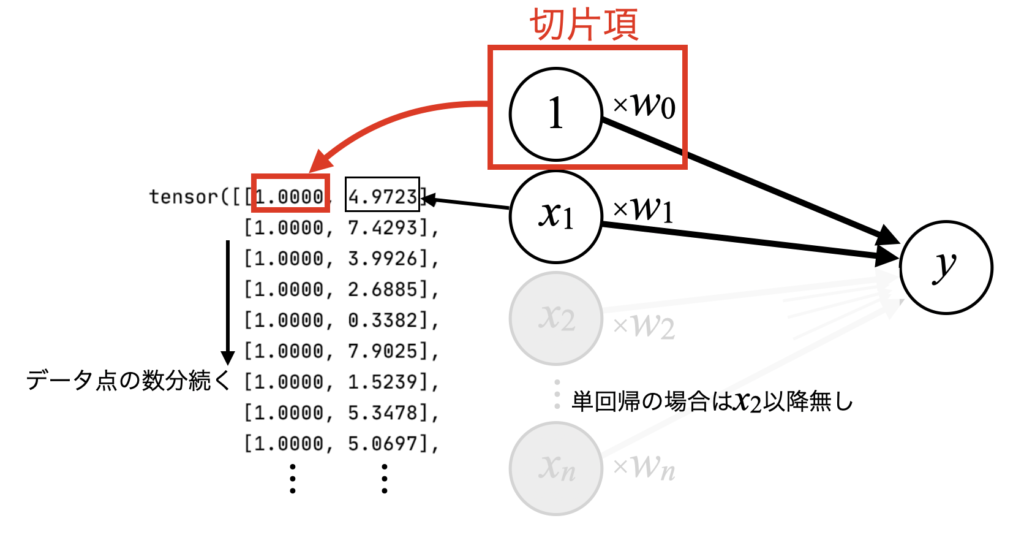
以下のコードでデータ点の数分全て1の配列を作り、xに対し左横方向に結合します。元々1次元のxという配列に対し、次元を追加する方法で結合するためstackを使っています。
|
1 |
X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 |
ネットワーク・最適化・損失関数の設定
ここがキーとなるネットワークの設定ですが、驚くほど簡単です。torch.nnを使ってLinearと線形ネットワークのインスタンスを生成します。このネットワークにはin_featuresとして特徴量の数(単回帰の場合切片も含めて2)を設定し、out_featuresはyのみなので1、切片は入力に含めたのでbiasはFalseにします。
最適化もSGDに先ほどのネットワークのパラメータと学習率lr(learning rate)を設定するのみで、損失関数も既に.MSELossが用意されています。
|
1 2 3 |
net = torch.nn.Linear(in_features=dimension, out_features=1, bias=False) # ネットワークに線形結合モデルを設定 optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 最適化にSGDを設定 E = torch.nn.MSELoss() # 損失関数にMSEを設定 |
学習ループ
設定を使って学習のループを回しますが、forループを使って反復計算を行います。
ループの始めに勾配情報をリセットし、ネットワークに訓練データであるxを渡して予測値を得ます。
次に損失を計算しますが、ここでは正解データyと予測データy_predのshapeを揃える必要がある事が注意点です。
あとは.backward()を使って勾配をバックプロパゲーションによって計算し、最適化の勾配情報から重みを更新します。損失値の蓄積は必須ではありませんが、後でどのように減っていったか、もしくは発散しそうなのかどうか評価する時に使うのであった方が良いでしょう。
|
1 2 3 4 5 6 7 8 9 |
# 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = net(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 |
回帰係数を取得する
学習が終了したら.weightで回帰分析の結果として重み\(w\)を受け取ります。後はプロットしたりするだけですので、このサンプルコードでは一度.data.numpyでNumpy形式に変換しています。その他は直線描画のために新しい横軸と、得られた回帰係数で縦軸の値を作成しているだけです。
|
1 2 3 4 5 |
# 回帰係数を取得して回帰直線を作成 w0 = net.weight.data.numpy()[0, 0] w1 = net.weight.data.numpy()[0, 1] x_new = np.linspace(np.min(x.T[1].data.numpy()), np.max(x.T[1].data.numpy()), len(x)) y_curve = w0 + w1 * x_new |
おまけ:GIF動画で単回帰の学習過程を観察するコード
おまけです。一生懸命ネットワークが学習している過程を動画にして観察するためのコードを紹介します。「Pythonで複数画像からGIFを作る時に便利な処理まとめ」で習得したGIF動画作成コードを使っています。
今回は10イタレーションで1枚の画像をoutフォルダに生成していき、最後にpytorch-learning-result.gifをプログラム実行ディレクトリに保存します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 |
import torch import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def linear_regression(dimension, iteration, lr, x, y): net = torch.nn.Linear(in_features=dimension, out_features=1, bias=False) # ネットワークに線形結合モデルを設定 optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 最適化にSGDを設定 E = torch.nn.MSELoss() # 損失関数にMSEを設定 # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = net(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 # 回帰係数を取得して回帰直線を作成 w0 = net.weight.data.numpy()[0, 0] w1 = net.weight.data.numpy()[0, 1] x_new = np.linspace(np.min(x.T[1].data.numpy()), np.max(x.T[1].data.numpy()), len(x)) y_curve = w0 + w1 * x_new # 10計算毎にプロットを保存 if (i + 1) % 10 == 0: # グラフ描画 plot(x.T[1], y, x_new, y_curve, losses, 'out', i) print(i) # GIFアニメーションを作成する関数を実行する create_gif(in_dir='out', out_filename='pytorch-learning-result.gif') return net, losses def plot(x, y, x_new, y_pred, losses, dir, index): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(0, 10) ax1.set_ylim(0, 30) ax2.set_xlim(0, 1000) ax2.set_ylim(0.1, 100) ax2.set_yscale('log') # データプロット ax1.scatter(x, y, label='dataset') ax1.plot(x_new, y_pred, color='red', label='PyTorch result') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses)-1], color='red') ax2.text(600, 30, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 50, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend(bbox_to_anchor=(0,1), loc='upper left') fig.tight_layout() # dirフォルダが無い時に新規作成 if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) #plt.show() plt.close() # ------------------------------------------------------------------- # GIFアニメーションを作成 def create_gif(in_dir, out_filename): path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # サンプルデータ x = np.random.uniform(0, 10, 100) # x軸をランダムで作成 y = np.random.uniform(0.2, 1.9, 100) + x + 10 # yを分散した線形データとして作成 x = torch.from_numpy(x.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(100), x], 1) # xに切片用の定数1配列を結合 # 線形回帰を実行 net, losses = linear_regression(dimension=2, iteration=1000, lr=0.01, x=X, y=y) |
生成される動画は以下のGIFです。順調に学習していき、正解が近くなると損失が減るスピードが遅くなるという素の勾配降下法の特徴が良く見れていますね。
PyTorchによる重回帰分析のコード
出力
続いて重回帰分析をするコードを書いていきます。単回帰の1変数から1つ増やして2変数とし、目標は下図のように、3Dプロットで確認できる所に置きます。

全コード
単回帰と同じ使い方なのであまり追加の説明はありませんが、以下にコピペしてすぐ動作する全コードを示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
import torch import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D def linear_regression(dimension, iteration, lr, x, y): net = torch.nn.Linear(in_features=dimension, out_features=1, bias=False) # ネットワークに線形結合モデルを設定 optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 最適化にSGDを設定 E = torch.nn.MSELoss() # 損失関数にMSEを設定 # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = net(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print(list(net.parameters())) # 回帰係数を取得して回帰直線を作成 w0 = net.weight.data.numpy()[0, 0] w1 = net.weight.data.numpy()[0, 1] w2 = net.weight.data.numpy()[0, 2] X1 = np.arange(0, 11, 2.0) # x軸を作成 X2 = np.arange(0, 11, 2.0) # y軸を作成 X, Y = np.meshgrid(X1, X2) # x軸とy軸からグリッドデータを作成 Z = w0 + (w1 * X) + (w2 * Y) # 回帰平面のz値を作成 # グラフ描画 plot_3d(x.T[1], x.T[2], y, X, Y, Z, losses) return net, losses def plot_3d(x1, x2, z, X, Y, Z, losses): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(0, 10) ax1.set_ylim(0, 10) ax1.set_zlim(0, 100) ax2.set_xlim(0, 1000) ax2.set_ylim(1, 500) ax2.set_yscale('log') # データプロット ax1.scatter3D(x1, x2, z, label='dataset') ax1.plot_wireframe(X, Y, Z, color='red', label='PyTorch result') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses) - 1], color='red') ax2.text(600, 30, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 50, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.view_init(10, 60) ax1.legend() fig.tight_layout() plt.show() plt.close() # ------------------------------------------------------------------- # サンプルデータ w0 = 50.0 # 定数 w1 = -1.4 # 係数1 w2 = -0.1 # 係数2 x1 = np.random.uniform(0, 10, 300) # ノイズを含んだx軸を作成 x2 = np.random.uniform(0, 10, 300) # ノイズを含んだy軸を作成 y = w0 + (w1 * x1) + (w2 * x2) + np.random.uniform(0, 5, 300) # ノイズを含んだ平面点列データを作成 x1 = torch.from_numpy(x1.astype(np.float32)).float() # xをテンソルに変換 x2 = torch.from_numpy(x2.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(300), x1, x2], 1) # xに切片用の定数1配列を結合 print(X) # 線形回帰を実行 net, losses = linear_regression(dimension=3, iteration=1000, lr=0.01, x=X, y=y) |
詳細コード説明
データの形
今回の2変数の場合は、下図に示すデータの形を使います。その他、nn.Linearに渡すin_featuresを切片数+説明変数の数にします。
3Dプロット
3DプロットはPyTorchを使った重回帰分析とは直接関係しませんが、本プログラムで使用している方法は「Python/matplotlib3Dプロット!面と散布図を作成」で書いている方法とほぼ同じです。
ただし、3Dプロットと2Dプロットを並べて表示させるために「ax1 = fig.add_subplot(121, projection='3d')」とprojectionを使ってsubplotを設定している所が少し違います。
おまけ:GIF動画で重回帰の学習過程を観察するコード
単回帰と同様に、おまけとして動画を生成するコードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 |
import torch import numpy as np from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D from PIL import Image import os import glob def linear_regression(dimension, iteration, lr, x, y): net = torch.nn.Linear(in_features=dimension, out_features=1, bias=False) # ネットワークに線形結合モデルを設定 optimizer = torch.optim.SGD(net.parameters(), lr=lr) # 最適化にSGDを設定 E = torch.nn.MSELoss() # 損失関数にMSEを設定 # 学習ループ losses = [] angle1 = 10 angle2 = 60 for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = net(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 #print(list(net.parameters())) # 回帰係数を取得して回帰直線を作成 w0 = net.weight.data.numpy()[0, 0] w1 = net.weight.data.numpy()[0, 1] w2 = net.weight.data.numpy()[0, 2] X1 = np.arange(0, 11, 2.0) # x軸を作成 X2 = np.arange(0, 11, 2.0) # y軸を作成 X, Y = np.meshgrid(X1, X2) # x軸とy軸からグリッドデータを作成 Z = w0 + (w1 * X) + (w2 * Y) # 回帰平面のz値を作成 # 10計算毎にプロットを保存 if (i + 1) % 10 == 0: # グラフ描画 angle1 -= 0.2 angle2 += 2 plot_3d(x.T[1], x.T[2], y, X, Y, Z, losses, 'out2', i, angle1, angle2) print(i) # GIFアニメーションを作成する関数を実行する create_gif(in_dir='out2', out_filename='pytorch-learning-result2.gif') return net, losses def plot_3d(x1, x2, z, X, Y, Z, losses, dir, index, angle1, angle2): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(0, 10) ax1.set_ylim(0, 10) ax1.set_zlim(0, 100) ax2.set_xlim(0, 1000) ax2.set_ylim(1, 500) ax2.set_yscale('log') # データプロット ax1.scatter3D(x1, x2, z, label='dataset') ax1.plot_wireframe(X, Y, Z, color='red', label='PyTorch result') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses) - 1], color='red') ax2.text(600, 30, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 50, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.view_init(angle1, angle2) ax1.legend() fig.tight_layout() # dirフォルダが無い時に新規作成 if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) #plt.show() plt.close() # ------------------------------------------------------------------- # GIFアニメーションを作成 def create_gif(in_dir, out_filename): path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # サンプルデータ w0 = 50.0 # 定数 w1 = -1.4 # 係数1 w2 = -0.1 # 係数2 x1 = np.random.uniform(0, 10, 300) # ノイズを含んだx軸を作成 x2 = np.random.uniform(0, 10, 300) # ノイズを含んだy軸を作成 y = w0 + (w1 * x1) + (w2 * x2) + np.random.uniform(0, 5, 300) # ノイズを含んだ平面点列データを作成 x1 = torch.from_numpy(x1.astype(np.float32)).float() # xをテンソルに変換 x2 = torch.from_numpy(x2.astype(np.float32)).float() # xをテンソルに変換 y = torch.from_numpy(y.astype(np.float32)).float() # yをテンソルに変換 X = torch.stack([torch.ones(300), x1, x2], 1) # xに切片用の定数1配列を結合 print(X) # 線形回帰を実行 net, losses = linear_regression(dimension=3, iteration=1000, lr=0.01, x=X, y=y) |
回転させたり色々やっていますが、以下のGIF動画を作る事が出来ます。単回帰の時より収束のスピードが下がっている気がしますね。
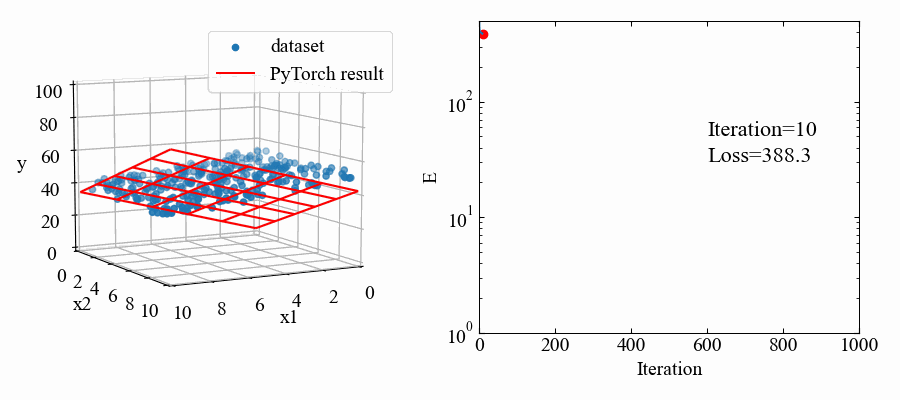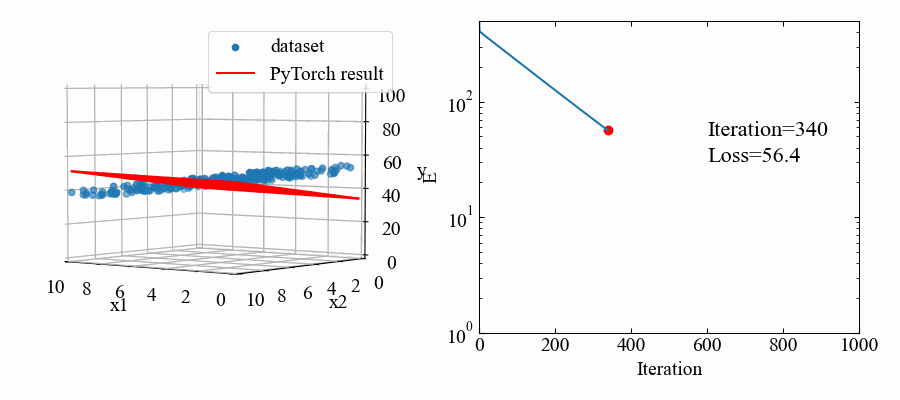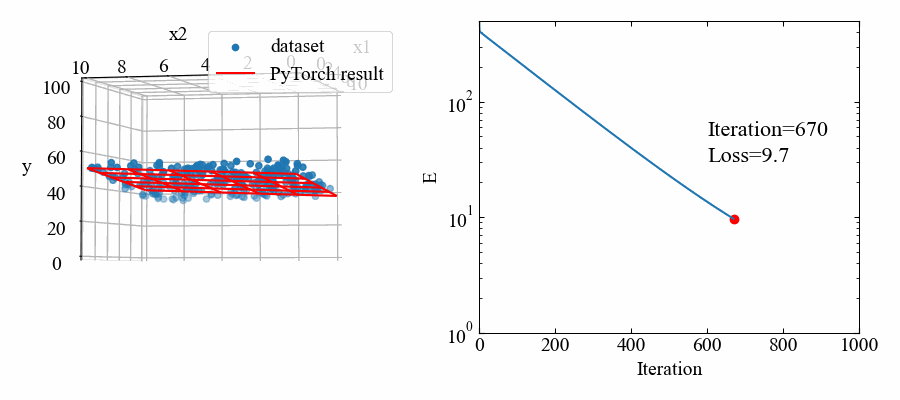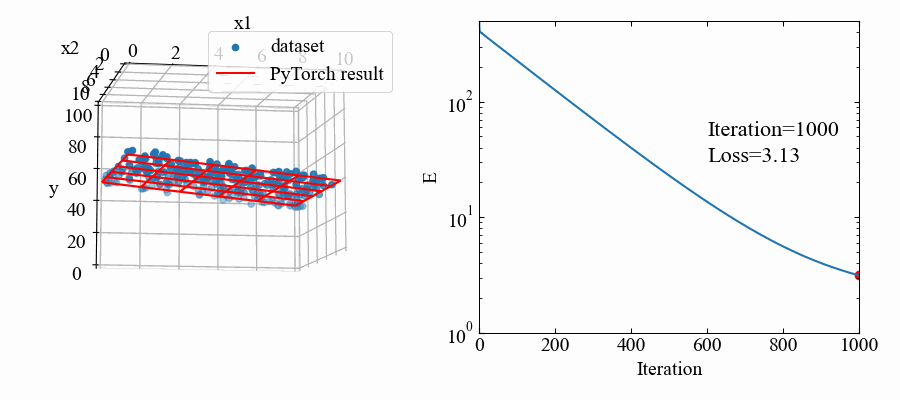
関連記事紹介
ネットワークモデルをクラスで書く
ゼロつく等の書籍を読むとわかるように、ディープラーニングのプログラムはオブジェクト指向プログラミングであるクラス(class)を使って書く方がすっきりします。
以下の記事は初心者(僕)がクラスによるPyTorchの使い方を覚えた時に書いた内容であるため、特に初心者の方に参考になると思います。
非線形回帰をする
線形回帰を行った後は、是非以下の記事を参考に非線形回帰に挑戦してみてください。ぐにゃぐにゃ曲がった関数に学習過程でフィットしていく様は見ものです。
まとめ
今回はようやくPyTorchを使い始め、回帰分析やPyTorchの概要と共に、実際にPyTorchによる回帰分析コードを単回帰と重回帰で書いてみました。
PyTorchはnnモジュールで簡単にネットワークを構築し、さらに最適化モデルをoptimで設定、損失関数もMSELossといった基本的なものは用意されていました。
学習ループもそれほど多いコードではなかったので、もう少し使い慣れれば詳細な構造を理解できてくるかも知れません。
今後は複雑な関数で回帰分析を行ったり、ニューラルネットワークをclassで書いたり…といったトレーニングに進もうと計画中です。
→上記関連記事に追記しました!
PyTorchのインストールからかなり時間が経ってしまいましたが、ようやく簡単なネットワークを構築してテンソル演算をする事ができました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント