JDLAが主催するG検定ではディープラーニングの全体像や各種問題点、手法に関する問題が出題されます。ここでは、ディープラーニングの概要と具体的な手法の紹介をしていきます。
こんにちは。wat(@watlablog)です。今回はG検定対策として、ディープラーニングの概要を学んだ結果をまとめます!
本ブログで学習結果を記録し、結果としてG検定に合格しました!皆さんも是非当ブログを参考にして下さい。

G検定に必要な知識
G検定学習のシラバスと本記事でまとめる内容
G検定とは、日本ディープラーニング協会(JDLA:Japan Deep Learning Association)が主催している認定試験です。
JDLA公式ページ:https://www.jdla.org/
G検定の概要は前の記事「【G検定の学習】人工知能(AI)の定義と分類を整理!」に記載していますので、最初から読みたい!という方は是非リンクをクリックしてみて下さい。
G検定の出題範囲はJDLAから「学習のシラバス」として公開されています。
この記事ではシラバスに記載されている「ディープラーニングの概要」をまとめ、ディープラーニングの全体像や計算の流れがおおまかに掴めるようになることを目指します!
参考書
僕の学習は「徹底攻略 ディープラーニングG検定ジェネラリスト問題集」で設問を解き、わからないことをWebやその他書籍で調べるというスタイルです。
※2022年2月現在はこちらの第2版が最新のようですのでリンクを更新しました。
ここでまとめている内容はディープラーニングの一般的な知識に関するものだけです。
著作権の関係上、本に記載されているような設問はここに載せることができませんが、G検定を受験する予定のある方は、当ブログ等で学習した実力確認として上記問題集を購入してみると良いかも知れません。
それでは早速説明していきます!
既にいくつかの知識をお持ちの方は、上にある目次から必要な所へジャンプしてみて下さい!
ディープラーニングの全体像
G検定では詳細なアルゴリズムの内容よりも、全体像を掴むことが重要とテキストに記載されています(G検定のGはジェネラリストであり、E資格のようなエンジニア視点では無いため)。
そのためこのページではまずディープラーニングの前身であるニューラルネットワークやニューロンについて触れ、その後にディープニューラルネットワークの特徴や問題点、各種手法の紹介を行います。
ニューラルネットワークとディープニューラルネットワーク
ニューラルネットワーク(NN)とは?
ニューラルネットワーク(NN:Neural Network)とは、人間の脳内にあるニューロン(神経細胞)のネットワークを模倣し、コンピュータで計算できるように定式化したモデルです(実際に脳科学的に詳細なニューロンをモデル化しているわけではありません)。
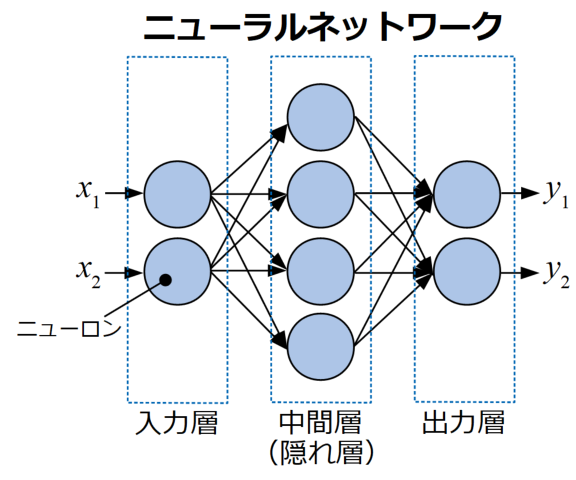
NNの例を下図に示します。このように、NNはニューロンと呼ばれる最小単位の要素が層を作って入力から出力までを行います。
ここで、データが入る最初の層を入力層、最後に値が出てくる層を出力層、途中の層を中間層(または隠れ層)と呼びます。
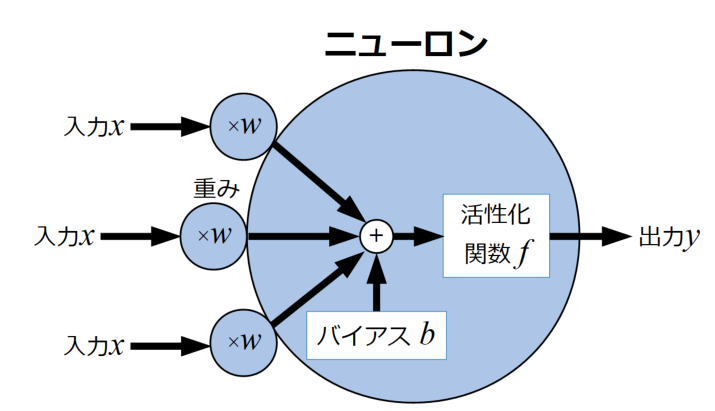
NNを構成している個々のニューロンモデルを下図に示します。
個々のニューロンは共通して入力\(x\)に重み\(w\)をかけあわせ、バイアス\(b\)を加算し、活性化関数\(f\)を通して出力値\(y\)を出力させます。
ニューロンの出力値計算方法
G検定ではニューロンの出力値を計算する問題が出る可能性がありますので、ここで上図のモデルを定式化してみましょう。
ニューロン出力値の計算式を以下の式(1)に示します。
\[
\begin{cases}
y=f(u) \\
u=\mathbf{w} ^{\mathbf{T}}\mathbf{x}+b
\end{cases} (1)
\]
ニューロンに入力される入力\(x_{i}\)や重み\(w_{i}\)は複数あるので、それぞれベクトル形式で書き、内積計算をしています。
ここでNNの活性化関数\(f\)は様々な関数が考えられ、それぞれの種類や特徴を「ディープラーニングにおける活性化関数をPythonで作る!」で詳細に説明していますので是非参考にしてみて下さい。
ちなみに「Pythonで多層パーセプトロンのXORゲートを実装する!」という記事でNNの前身であるパーセプトロンを紹介しましたが、パーセプトロンの活性化関数はステップ関数です。
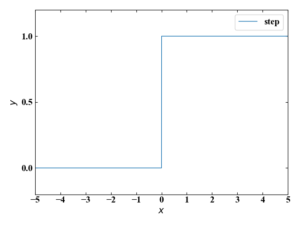
ステップ関数は\(u\)=0で微分出来ないためNNの学習では使用出来ません。
そこで、ステップ関数と形が似ていて、かつ微分可能な関数としてシグモイド関数がNNの研究初期に活性化関数として使われることが多くあったそうです。
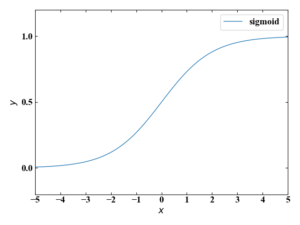
しかしこのシグモイド関数は本ページの後半で説明する勾配消失問題が起きやすいという理由で現在あまり使われていません。
勾配消失問題が起きにくい関数として現在最も使われているのがReLU関数です。
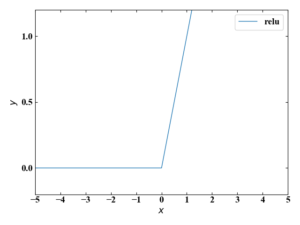
このReLU関数は中間層でよく使われます。
また、出力層では総和が1になるように値をスケーリングするソフトマックス関数がよく使われます。
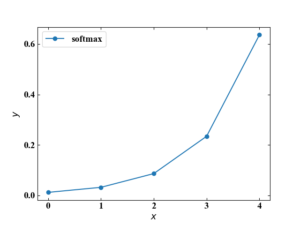
このように活性化関数を適材適所で使ってニューロンの出力値を計算しているんですね!
ディープニューラルネットワーク(DNN)とは?
ディープラーニングはディープニューラルネットワーク(DNN:Deep Neural Network)を使った学習法で、先ほどまでのNNとニューロンを使ってネットワークを構成する所までは同じですが、特に層を深く繋げたもののことを呼びます。
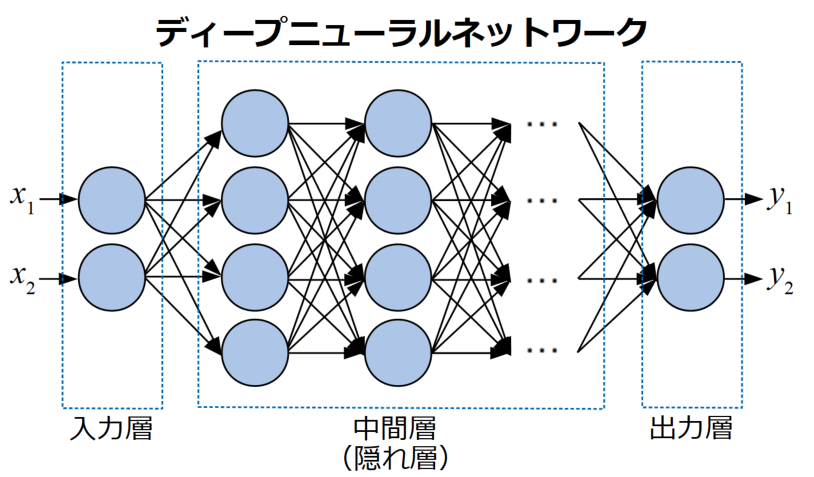
このように層を沢山連ねることで表現力を増やし、複雑な関数を近似できるようになります。
ディープラーニングのアルゴリズム自体は1960年代には考案されていましたが、近年のコンピュータ技術の劇的な進化により実用レベルで利用可能になりました。
ディープラーニングの学習の流れ
ディープラーニングの学習の流れを理解するためには、まず各層がどのような役割をし、どういったデータフローとなっているかを学ぶのが第一歩です。
ここでは、基本的なDNNを入力層、中間層、出力層と分けてその役割を説明していきます。
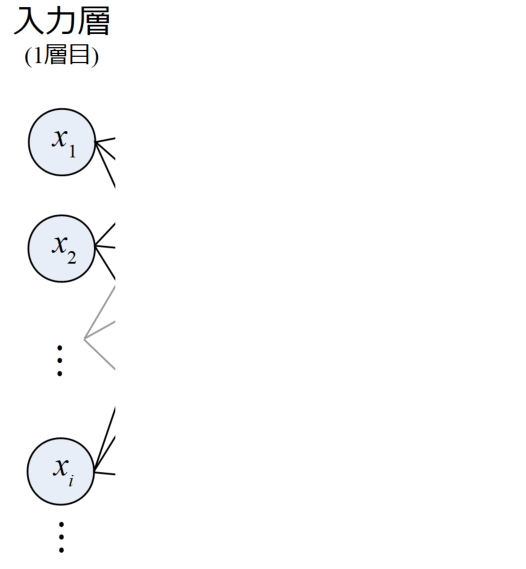
入力層
ネットワークの中で最も簡単なのが入力層(Input layer)です。
この層はデータ値をそのまま出力し、中間層へ渡します。
画像であれば各ピクセル位置の輝度値を入力ベクトルへ変換したものとなります。
中間層
中間層(Intermediate layer)は前の層の値を受け取ってニューロンの計算を行います。以下の図は入力層から最初の中間層へのデータフローを表した図です
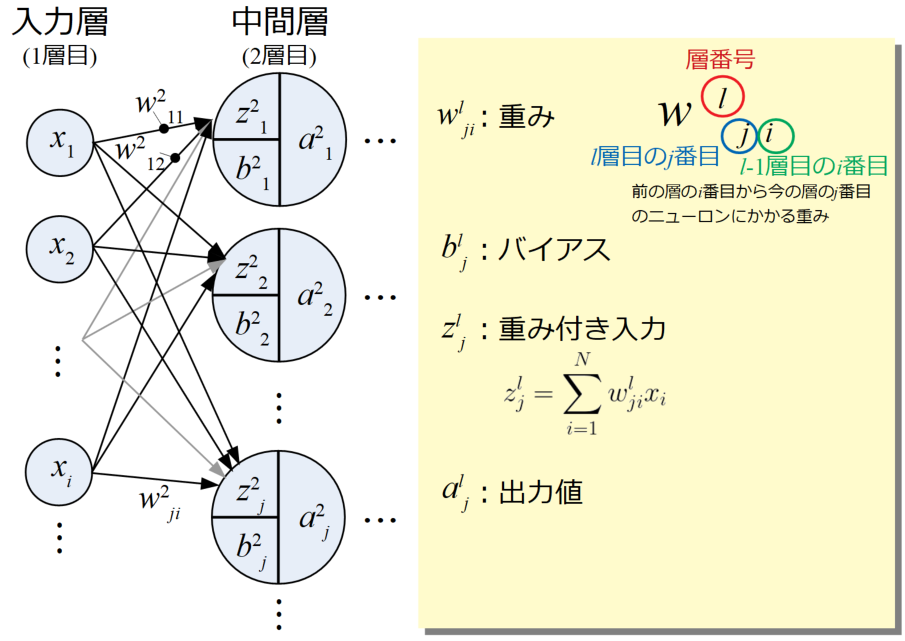
入力層からは単純に入力値\(x_{i}\)の値が中間層に届きますが、どこから来た入力かによってそれぞれ固有の重み\(w\)がかけられます。
この重みは数々の表記法がありますが(まだ標準化されていないかも)、ここではおそらくこの方法が一番多いのではないかという表記にしています。
重み\(w^{l}_{ji}\)は「前の層(\(l-1\))の\(i\)番目から今の層(\(l\))の\(j\)番目に来た重み」を意味し、\(l\)は指数ではありません。
さらに、ここでは\(l\)層\(j\)番目の重み付き入力\(z^{l}_{j}\)として重みと入力をかけた総和を求めています(式(2))。
\[
z^{l}_{j}=\sum_{i=1}^{N}w^{l}_{ji}x_{i} (2)
\]
中間層に入ってくる固有の重みと入力、方向の意味合いを表現するためにあえてシグマ(Σ)を使っていますが、やっている計算は上で紹介したニューロンの計算方法である式(1)のベクトル内積部分\(\mathbf{w} ^{\mathbf{T}}\mathbf{x}\)に過ぎません。 ここにバイアス\(b^{l}_{j}\)を加算すればニューロンにおける式(1)の\(u\)と同じです。
\(a^{l}_{j}\)は\(l\)層\(j\)番目における活性化関数による計算後の出力値です。これも式(1)の\(f(u)\)と同じです。
3層目から\(L-1\)層目(\(l\)(layer)ではなく\(L\)はラストの層を意味)までの中間層は入力\(x_{i}\)ではなく前の層の中間層から流れてくる\(a^{l-1}_{i}\)です。
3層目以降の中間層の重み付き入力は式(3)となります。
\[
z^{l}_{j}=\sum_{i=1}w^{l}_{ji}a^{l-1}_{i} (3)
\]
ここでは何個来るかを明示していないため、Σ記号の上には何も書いていません。
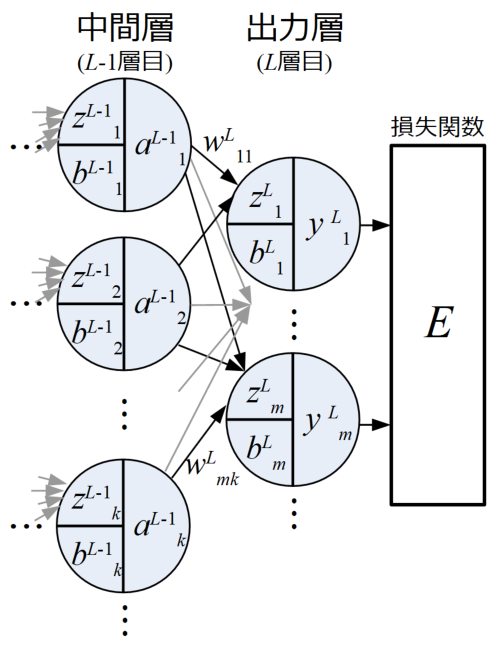
出力層
出力層(Output layer)は最後の予測値\(y\)を算出する重要な層です。
ここまでの各ニューロンの計算は活性化関数に何を選ぶかという違いはありますが、全て式(2)や式(3)と同様です。
最終的に出力層を通った値は全て損失関数(または誤差関数やコスト関数とも呼ばれる)に入力され、正解データと比べてどの程度差があるかを比較します。
予測値の流れは順伝播
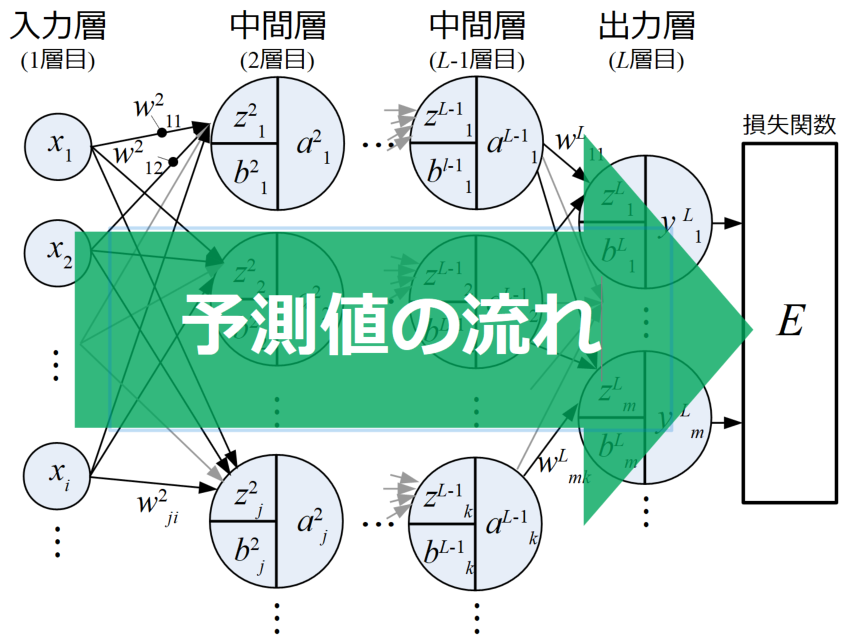
以上の各層をまとめ、ディープニューラルネットワーク(DNN)の例を図で示したものが下図です。
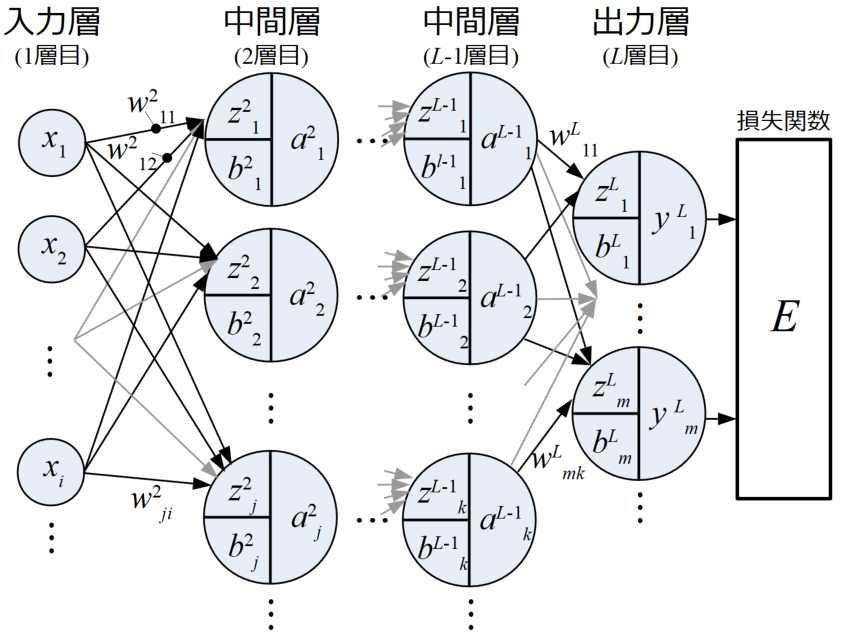
ここでは基本的なDNNについて述べていますが、入力から出力までの予測値の流れは下図に示すように左から右に流れていることがわかります。
このような予測値の流れ方を順伝播(Forward propagation)と呼びます。
誤差逆伝播(バックプロパゲーション)
先ほど予測値は順伝播をしていると説明しましたが、予測値は一回損失関数に渡されておしまいではなく、評価結果によって重みを更新していく工程があります。
重みの更新はこれから機械学習のモデルを構築するという時に、各重みが大きくなれば良いか小さくなれば良いか(誤差が小さくなるか)を最適化することが必要です。
その判断指標に各ニューロンにおける勾配の情報を使い、最もポピュラーな方法に勾配降下法(Gradient discent)による推定があります。
勾配降下法のイメージ図を以下に示します。勾配降下法は損失関数を最小にする重み(各ニューロン分の重みがあるので、重みは多変数となる)を探す最適化(Optimization)と呼ばれる計算を行います。
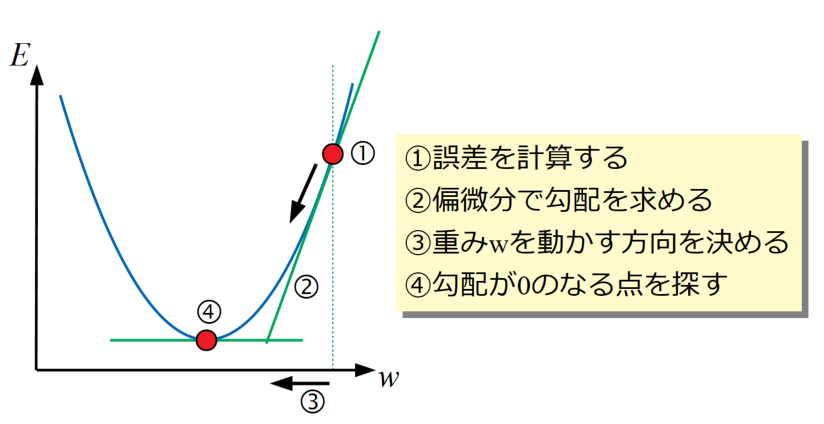
要は関数の勾配(傾き)が0になる場所を探せばよいので、①誤差を計算した後は微分問題を解くことになります。
そして重みは多変数なので、②偏微分の形式をとります。
勾配がわかれば③重みを動かす方向と量を決め、④勾配が0になるまで①~③を繰り返します。
ここで、真面目に勾配を一つ一つ計算していくと、膨大な量の偏微分を解かなければならないのですが、微分には連鎖率と呼ばれる法則があり、この連鎖率を使うと各ニューロンにおける誤差を出力層から逆に連鎖的に求めることが可能になります。
図にすると誤差の流れは出力層から入力層に向かって逆伝播していきます。重みの更新もこの時行われ、この一連の重み更新方法を誤差逆伝播法(バックプロパゲーション:Back propagation)と呼びます。
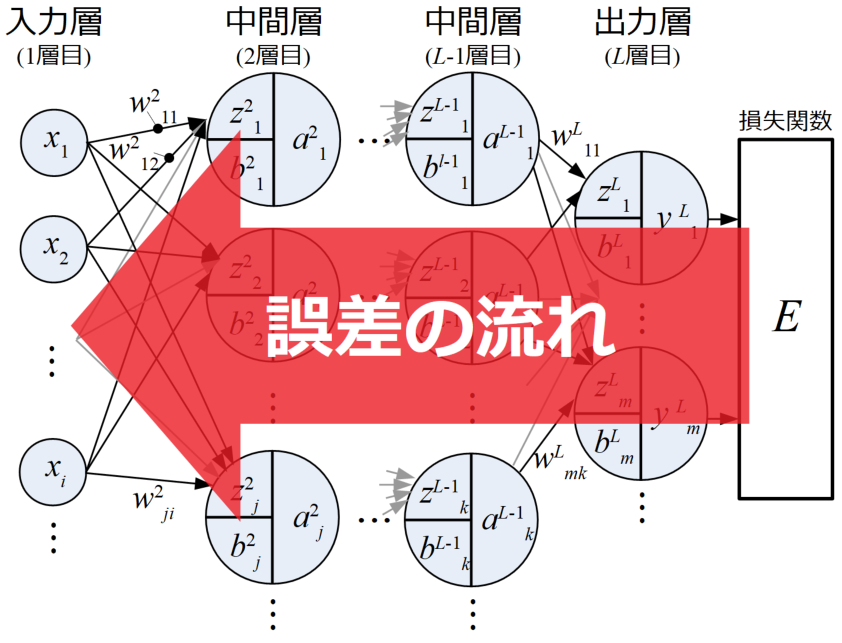
G検定ではDNNの学習のおおまかな流れと誤差逆伝播法の概要がわかっていれば良さそうです。
数式を使った説明はこの後僕が完全に理解したら別記事を作成する…かも知れません!
大域的最適解と局所最適解
損失関数の傾きが0になる点は下図に図示した3種類です。
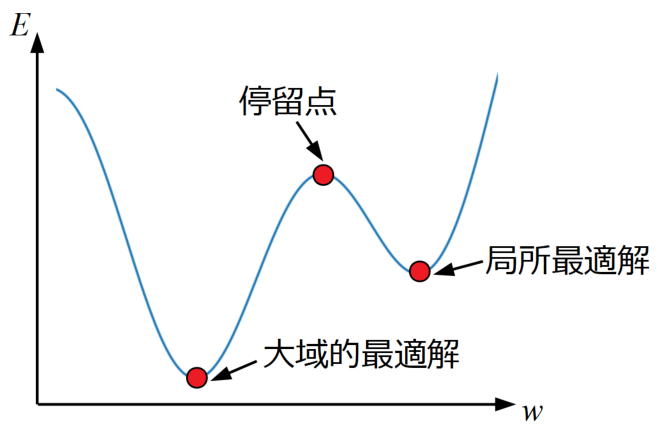
停留点(Stationary point)は最小値では無いので目指すべき点ではありません。
大域的最適解(Grobal optimum solution)は損失関数全体で最も誤差が小さくなる点であり、本来目指す点です。
局所最適解(Local optimum solution)はその周辺では最小値をとりますが、関数全体の最小値ではない点です。
本来目指すべきは大域的最適解ですが、勾配降下法による探査は基本的に局所最適解で妥協するしかないとのことです。
イテレーションとエポック
勾配降下法によって重みを更新していくためには、複数回の計算を回す必要があります。
ここで、重みを更新した回数(計算回数)をイテレーション(Iteration)と呼びます。
訓練データを学習に使った回数はエポック(Epoch)と呼ばれるので、これらの用語が混同しないように気を付けましょう
学習法分類
ネットワークの学習法には訓練データの使い方にいくつかのパターンがあります。ここでは代表的な3つの学習法を紹介します。
バッチ学習
バッチ学習(Batch learning)とは、訓練データ全ての誤差を計算し重みを1回更新することを繰り返す学習法です。この方法で行われる勾配降下法をバッチ勾配降下法と呼ぶことがあります。
バッチ学習は訓練データのノイズ(外れ値等)の影響を受けにくいメリットがありますが、一度に扱うデータ量が多く計算が遅いといったデメリットもあります。
ミニバッチ学習
ミニバッチ学習(Mini-batch learning)とは、訓練データからランダムにサンプリングした小さなまとまり(ミニバッチ)を使って学習する方法です。
ミニバッチ内の全データの誤差総和を使い、この方法で行う勾配降下法をミニバッチ勾配降下法と呼びます。
ミニバッチ学習はバッチ学習に比べ学習に使用するデータを少なくできるメリット(計算量が少なくなる)があります。
逐次学習(オンライン学習)
逐次学習またはオンライン学習(Online learning)とは、1つの訓練データに対し重みの更新を1回行う学習法です。
逐次学習で行う勾配降下法を確率的勾配降下法(SGD:Stochastic Gradient Descent)と呼び、単にSGDと呼ばれることが多くあります。
逐次学習は重みの更新1回が速いメリットがありますが、個々のデータのノイズ影響が他の方法よりも大きくなるデメリットがあります。
ディープラーニングが抱える問題
過学習と汎化誤差・訓練誤差の関係
機械学習の目的は未知のデータの振る舞いを予測することです。そのため訓練データとの誤差(訓練誤差)が小さければ良いということはないため、訓練に使っていないテストデータとの誤差(汎化誤差)を考慮する必要があります。
下図はイテレーションを横軸、誤差\(E\)を縦軸に汎化誤差と訓練誤差をプロットした例です。
(a)はイテレーションの増加と共に訓練誤差と汎化誤差が両方低下しているため、学習はうまくいっていると判断可能です。
一方、(b)はイテレーションの増加と共に訓練誤差は低下していっていますが、汎化誤差はある所から増加傾向を示しています。

これは訓練データに過剰にフィッティングしてしまったことが原因で発生する過学習(オーバーフィッティング)という現象です。
DNNは多層のニューロンにより複雑な関数を近似できる表現力を持っていますが、その表現力はそのまま過学習しやすいという問題に直結します。
この過学習しやすいという問題を改善するために、正則化を行ったり、重み更新時にランダムに一定の割合でニューロンを無効化するドロップアウトという手法を採用したり、様々な方法が考えられています。
正則化については「Python機械学習初心者用!サポートベクターマシンの概要と実装」で紹介したサポートベクターマシンにもCというパラメータで使われていましたね。
古典的機械学習でも過学習との闘いは避けられませんでした。
勾配消失問題と活性化関数の関係
ディープラーニングの問題の1つに、勾配消失問題があります。
勾配消失問題とは、学習の最中に偏微分で求める勾配情報が非常に小さくなりなくなってしまうことで、それ以上学習が進まなくなることを言います。
先ほどの過学習と同じく、ニューロンを多層化すると多彩な表現力を得ることができますが、誤差逆伝播法は出力層から入力層に向かって勾配計算から連鎖的に重み更新を進めて行くので、1つでも学習停止したニューロンがあればそこから先に繋がった全てのニューロンの重みも更新されなくなります。
NNが使われ始めた当初は中間層の活性化関数にシグモイド関数がよく使われていましたが、シグモイド関数は正規化機能があるので、勾配が0付近の値になることがあります。
微分の連鎖率は合成関数の微分公式を多変数関数に拡張したものと考えれば、1つでも0近傍の値があると層が深いほど勾配が消失しやすくなる理屈も容易に理解できますね。
NNの勾配消失問題を改善するために、活性化関数に正規化機能の無いReLU関数(ランプ関数)を使うことが考案されました。
ReLU関数を使うことで勾配消失問題は起きにくくなり、現在では画像処理や自然言語処理を始めとした様々な領域で大きな成果をあげていますが、活性化関数以外のパラメータでも勾配消失問題は発生し得るので未だに問題としては存在しています。
各ニューラルネットワーク技術の繋がり
本記事はディープラーニングの概要として、おおまかな技術・特徴を紹介してきました。ディープラーニングは現在も多く研究されており、ディープニューラルネットワークを使った様々なアルゴリズムが開発されています。
ここでは詳細な説明はしませんが、簡単にそれぞれのNN技術の繋がりを紹介します。
以下の図はNNの基礎となるパーセプトロンから、現在主流となっているDNN派生技術の繋がりを示した図です。
パーセプトロンを多層にして活性化関数を使用するNNがDNNの基礎になっていますが、DNNはCNN、RNN、GAN、オートエンコーダという技術の基礎になっています。
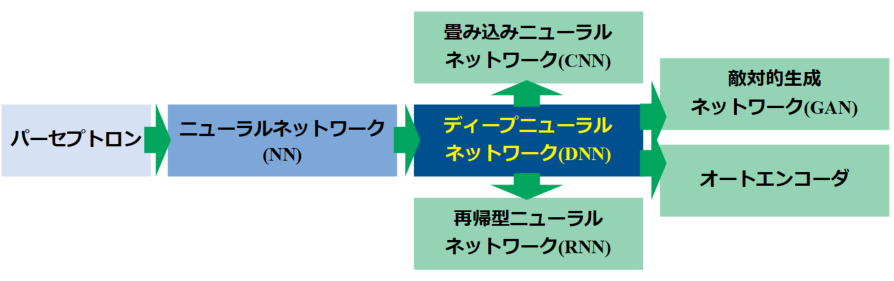
畳み込みニューラルネットワーク(CNN)
畳み込みニューラルネットワーク(CNN:Convolutional Newral Network)とは、主に画像認識の分野に適したDNNで、自動運転技術にも使われています。
畳み込み層、プーリング層、全結合層といった層を持つことが特徴です。
特にG検定では畳み込み層の演算(コンボリューション)についての問題が出る可能性があります。
この畳み込み演算は画像処理の分野では古くから画像をぼかしたり、エッジを際立たせたりといったフィルタ処理に使われていました。
CNNで行う畳み込みも同様であり、入力データ(画像)に対しフィルタ(カーネルとも呼ぶ)による畳み込み演算を行います。この時得られた結果を特徴マップと呼びます。
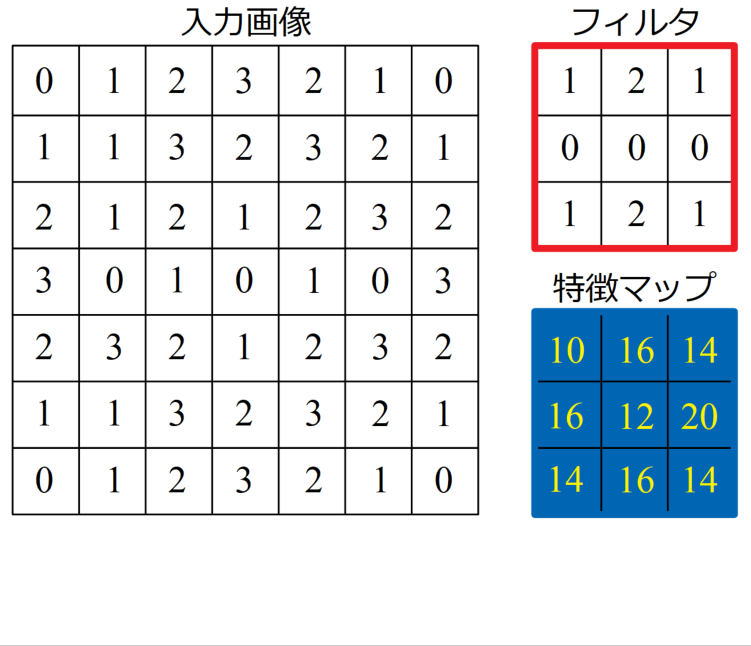
この特徴マップは積和演算と呼ばれる計算をします。入力画像に対し、フィルタを当てはめ、座標が対応する要素同士をかけていき、最後に足し算をした結果を特徴マップに埋め込んでいきます。言葉や式では中々伝わりにくい計算ですが、以下に計算手順を示したGIF動画を載せます。
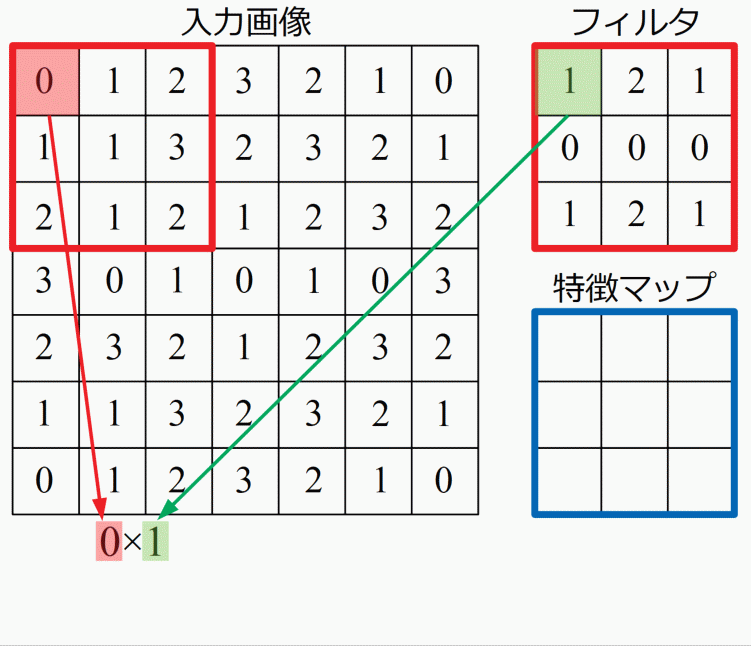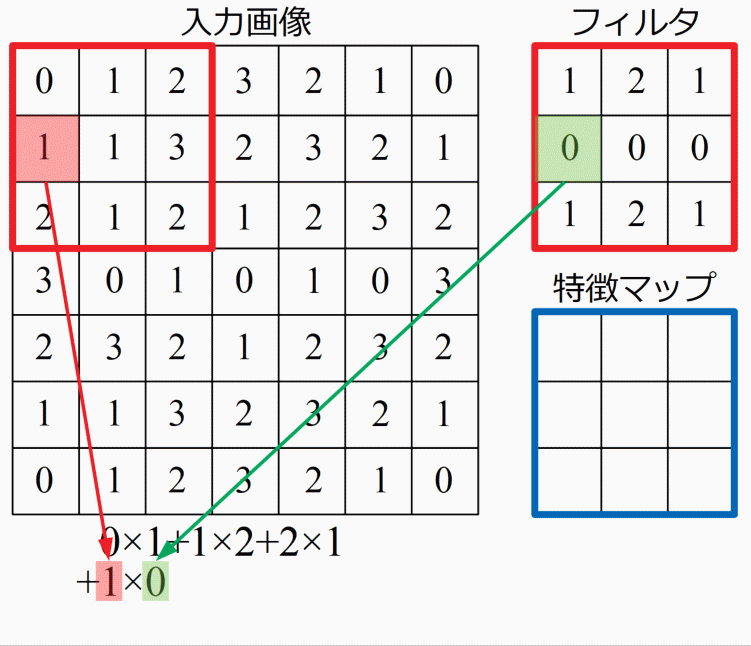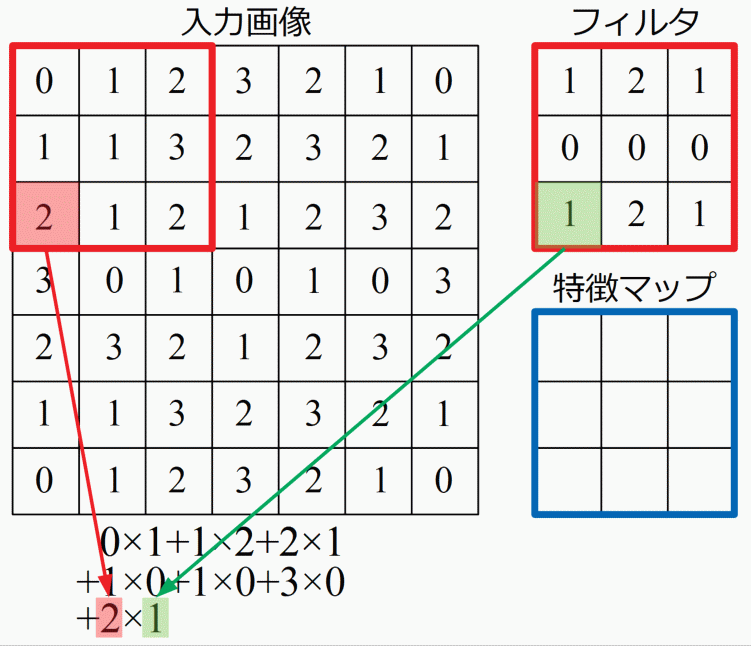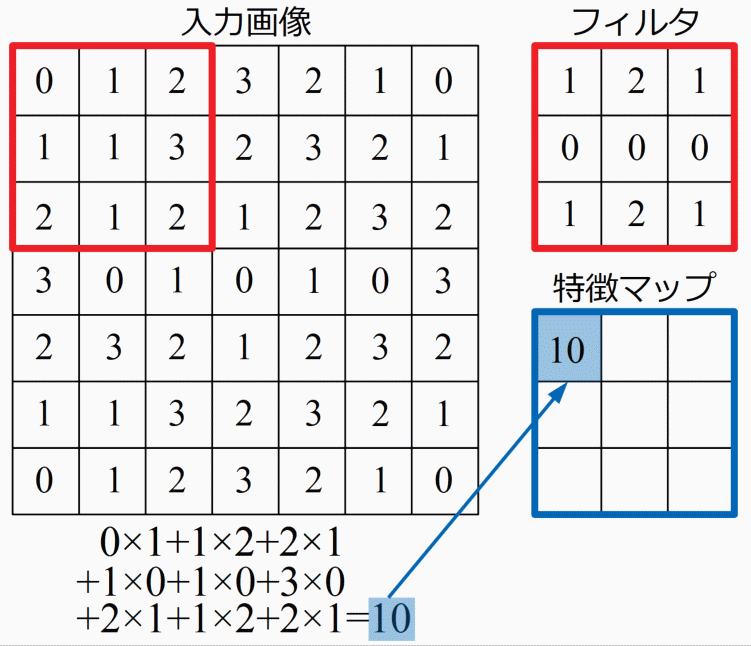
フィルタの全座標分の計算が終了したら、次はフィルタを順次ずらして同様の計算をしていきます。この時、フィルタを移動させる刻みをストライドと呼びます。下の画像のストライドは2です。
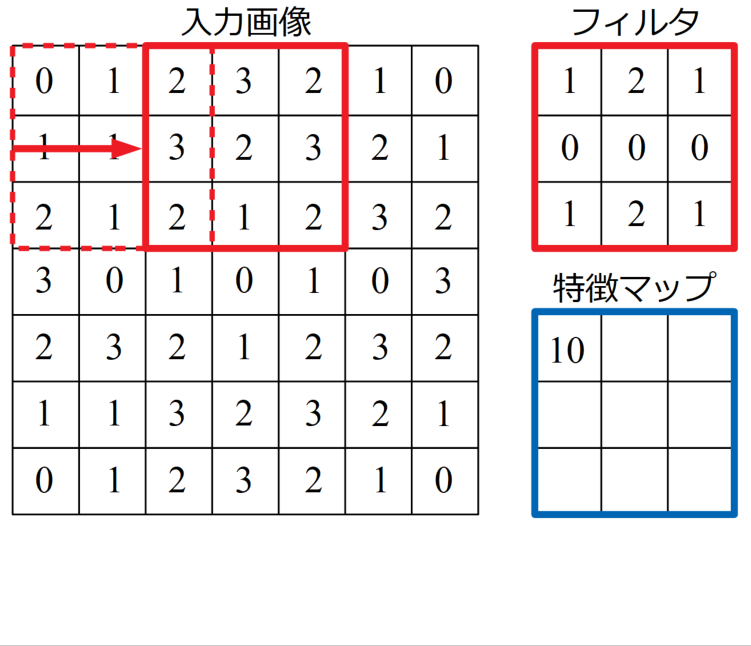
今回用意したサンプルの全計算手順は以下のYoutube動画に載せましたので、まずは計算の流れを把握しましょう。
また、畳み込みの前にパディングと呼ばれる処理を行う場合もあります。パディングとは、画像の周りに新たなピクセルを付け足すことを意味します。
パディングを行うことで、幾層にも畳み込みを行う際に画像がどんどん小さくなっていくことを避けることが可能です。
下図は大きさ1のパディング(入力画像(青)の周囲を1ピクセルずつ囲む(赤)こと)です。特に、このパディングしたピクセルの値を0にすることをゼロパディングと呼びます。

実際の問題は、フィルタの数値が小数になる場合があります。検定は時間と正確さの勝負!使いやすい電卓があると便利だと思います!
再帰型ニューラルネットワーク(RNN)
再帰型ニューラルネットワーク(RNN:Recurrent Neural Network)とは、主に時系列データ処理の分野に適したDNNで、自然言語処理技術等に使われています。ネットワークに過去の情報を保持し戻って来る閉路を持つ特徴があります。
敵対的生成ネットワーク(GAN)
敵対的生成ネットワーク(GAN:Generative Adversarial Network)とは、実在しないデータを生成したり、既存データの特徴を使って他のデータを変換することができるDNNです。この技術は教師なし学習の一種で、ありもしない架空の画像を生成したりといった大変興味深いことが可能です。
オートエンコーダ
オートエンコーダ(Autoencoder)は自己符号化器とも呼ばれ、次元圧縮を行うNN(中間層1層で使うこともあり、中間層が2層以上になればDNN)です。
入力層と出力層のノード数が同じで、中間層がこの数よりも少なく、出力の結果を入力に近づけるように学習するアルゴリズムをとることが特徴です。
このアルゴリズムは生成ネットワークで訓練データと似せたデータを生成し、識別ネットワークでそのデータが訓練データか生成されたものかを識別するように学習していきます。
「中間層でノード数(ニューロンの数)を少なくしても出力層で入力層と同じ値が得られれば、中間層では入力データを再現する特徴のみを抽出できたと言う事ができる」というのがこのアルゴリズムの根本にあり、非線形の主成分分析ができることを意味します。
非線形の主成分分析ができれば、もしかして自動で特徴量エンジニアリングをするAIとかが登場するかも知れませんね!
それが出来れば、やりたいことを指示するだけでデータ収集からモデル生成までも自動でやっちゃうAIもできるかも??
まとめ
本記事ではG検定対策として、JDLAに公開されている学習のシラバスから「ディープラーニングの概要」について学習した結果をまとめています。
G検定はジェネラリストのための検定であるため、深いコーディング力ではなく全体の概要をしっかりと把握しているかを問われます。
本ページではディープラーニングの計算がどのように進められているか、どういった学習方法があるか、どのような問題を抱えているか、関連技術に何があるか…をまとめました。
ここで学んだ内容は以下の問題集第5章と第6章の前半で実力チェックが出来ますので、本を傍らに置いてこのページを見ると学習効率が良いと思います。
ディープラーニングの全体像がだんだんとわかってきたような気がします!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント