Python/sympyとnumpyで書くニュートン-ラフソン法

方程式系を数値解析的に解く方法としてニュートン-ラフソン法があります。有名な手法で記事も沢山ありますが、ここではPythonのsympyを使って記号的に本手法を書いてみます。

こんにちは。wat(@watlablog)です。簡単で便利な手法であるニュートン-ラフソン法をPythonのsympyで書いてみます！

目次（項目クリックでジャンプできます）

ニュートン・ラフソン法の概要と例題

ニュートン・ラフソン法とは？

ニュートン法(Newton's method)、またはニュートン-ラフソン法(Newton-Raphson meshod)とは、方程式系を反復法によって数値解析をする手法のことです。

かの有名なアイザック・ニュートンとジョセフ・ラフソンに由来して名付けられた手法です。

ニュートン-ラフソン法は以下の漸化式(1)で示されます。

\[ x_{n+1}=x_{n}-\frac{f(x_{n})}{f{(x_{n})}'} \tag{1} \]

漸化式とは、前の項を使って次の項を説明した式のことです。
式(1)は関数\(f(x)\)の\(x\)に前の値\(x_{n}\)を代入、\(x_{n}\)における関数\(f(x)\)の微分係数（つまり傾き）を使って次の値\(x_{n+1}\)を求めるための式です。

式と言葉だけよりも、実際に問題を解いた方が理解しやすいと思うため以下に例題を使って解説をしてみます。

例題:ニュートン-ラフソン法で\(\sqrt{2}\)の近似値を求める

問題

ニュートン-ラフソン法を初めて学習した人が必ずといって良いほど触れる有名な例題として、平方根の近似値計算があります。

\(\sqrt{2}\)は1.414…といった無理数であることは既に分かっています。\(\sqrt{2}\)は「ひと世ひと世にひと見ごろ」と語呂が良く覚えていられますが、\(\sqrt{n}\)と全ての\(n\)について暗記している方はいません（いませんよね？）。

例えば、急にある値の平方根をPCもスマホも電卓も使わないで求めなければいけない状況に陥った時に、ニュートン-ラフソン法は活躍します。

ニュートン-ラフソン法は方程式の解を数値計算するための手法です。今回の「2の平方根の近似値を求める」という問題を、「方程式の解を求める」に置き換えて解決していきましょう。

下図は今回の問題に対してニュートン-ラフソン法を適用するための前段階として設定した方程式\(f(x)\)です。

\(x^{2}=a\)の解は\(\pm\sqrt{a}\)になることは自明なので、この方程式\(x^{2}-a=0\)を数値的に解けば、\(\sqrt{a}\)の数値（\(\sqrt{a}\)で終わらず、小数点形式のfloat型で）が求まることになります。

漸化式で計算する

式(1)を今回の方程式の場合に書き換えると、式(2)の漸化式を得ます。

\[ x_{n+1}=x_{n}-\frac{x^{2}-2}{2x} \tag{2} \]

この式に初期値\(x_{n}\)として2を代入してみると、式(3)と展開し、1.5という数値を得ることができます。

\[ \begin{align} x_{n+1}&=x_{n}-\frac{x^{2}-2}{2x} \\ &=2-\frac{2^{2}-2}{2\times2}=1.5 \tag{3} \end{align} \]

ここで求めた1.5という数値は以下の図のように、\(x=2\)の接線と\(x\)軸との交点の\(x\)座標を意味しています。

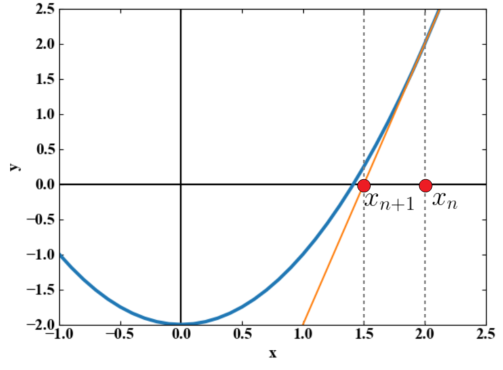
では続いて先ほど得られた1.5を初期値に入れ替えて同様の計算を式(4)と進めてみます。

すると、今度はより真の解に近づいた結果を得ました。

\[ \begin{align} x_{n+1}&=x_{n}-\frac{x^{2}-2}{2x} \\ &=1.5-\frac{1.5^{2}-2}{2\times1.5}=1.41666... \tag{4} \end{align} \]

式(5)と計算を進めるとさらに真の解に近づくのは予想通り。「ひと世ひと世に…」まで合ってきましたね。

\[ \begin{align} x_{n+1}&=x_{n}-\frac{x^{2}-2}{2x} \\ &=1.5-\frac{1.41666...^{2}-2}{2\times1.41666...}=1.4142156... \tag{5} \end{align} \]

ニュートン-ラフソン法の計算図解

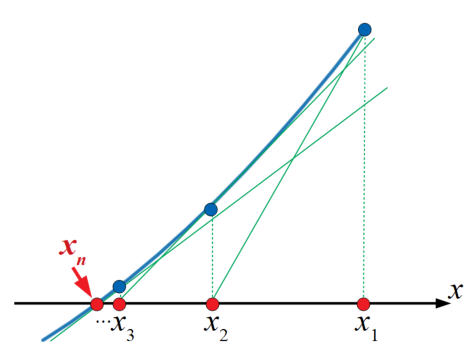
下図にニュートン-ラフソン法の計算過程を示します（どこでも載っているような図ですが）。

このように初期値\(x_{1}\)を決定した後は、式(1)の漸化式を反復計算に使用し、\(x_{2}, x_{3}, \cdots, x_{n}\)まで計算を行うことで方程式の解に近似するという仕組みです。

Python/sympyを使ったニュートン-ラフソン法のコード

sympyを使う理由と概要

Pythonでニュートン-ラフソン法を実装している記事は沢山ありますが、sympyを使った内容は見当たりませんでした。

sympyは方程式をxやyといった記号(Symbol)でそのまま処理をすることが可能です。通常、ニュートン-ラフソン法のプログラムは微分項を予め計算しておいてコードに落とし込む必要があります。

その場合は方程式が変化する度にコードレベルで微分をし直す必要があり、メンテナンス性が悪くなりがちです。その他、勾配情報を算出してから微分係数を求める方法もありますが、しっかり微分をしない場合は精度が若干落ちたり、コードが煩雑になりがちです。

sympyを使えばこれら両方の問題に対応することができると考え、今回コード化してみました。

sympyのインストールや使い方については「Python/sympyでテイラー展開した結果をグラフ化する方法」に記載していますので、ご興味があれば是非ご確認下さい。

全コード

以下にPythonのsympyとnumpyを使ったニュートン-ラフソン法のコードを示します。方程式は例題で解いたものと同じです。

本手法は理論的には無限に計算を繰り返してしまいますので、resとthresholdを使って漸化式の計算ループを制御しています。sympyのdiffを使った微分やsubsを使った値の代入は先ほど紹介した記事にも似たような内容があります。

import numpy as np
from sympy import*

# sympyを使ったニュートン-ラフソン法の関数
def newton_raphson(f, x1):
    fx = diff(f, x)                                         # 式の微分
    threshold = 1e-6                                        # 計算打ち切り閾値
    res = threshold + 1                                     # 残差(初期値は閾値より大きくしておく)

    # 残差が閾値より小さくなるまでループを回す
    while res > threshold:
        x2 = float(x1 - (f.subs(x, x1) / fx.subs(x, x1)))   # ニュートン-ラフソン法の漸化式
        res = np.abs(x2 - x1)                               # 前の値と今の値の残差
        print(x1)
        x1 = x2
    return x2

# sympy変数、展開する式の定義と関数実行
x = Symbol('x')
f = x ** 2 - 2
x1 = newton_raphson(f, x1=2)

import numpy as np

from sympy import*

# sympyを使ったニュートン-ラフソン法の関数

def newton_raphson(f, x1):

fx = diff(f, x) # 式の微分

threshold = 1e-6 # 計算打ち切り閾値

res = threshold + 1 # 残差(初期値は閾値より大きくしておく)

# 残差が閾値より小さくなるまでループを回す

while res > threshold:

x2 = float(x1 - (f.subs(x, x1) / fx.subs(x, x1))) # ニュートン-ラフソン法の漸化式

res = np.abs(x2 - x1) # 前の値と今の値の残差

print(x1)

x1 = x2

return x2

# sympy変数、展開する式の定義と関数実行

x = Symbol('x')

f = x ** 2 - 2

x1 = newton_raphson(f, x1=2)

以下に上記コードの実行結果を示します。
初期値の2から反復計算を経て最終的には1.41421356…と真値に近づく結果を得ました。

2
1.5
1.4166666666666667
1.4142156862745099
1.4142135623746899

1.5

1.4166666666666667

1.4142156862745099

1.4142135623746899

まとめ

本記事ではニュートン-ラフソン法の概要と例題を確認し、Python/sympy/numpyでコードを書いてみました。

sympyを使うことで方程式を記号そのままで記述し、正確な微分と共にシンプルにプログラム化することが出来ました。

方程式の近似解を得る武器をまた1つ得ることが出来ました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

吉より:

2023年6月1日 4:48 PM

三次方程式の時のコードを教えてください。

返信
1. wat より:
  
  2023年6月5日 1:13 AM
  
  ご訪問ありがとうございます。
  以下のように、f=の部分に任意の方程式を記述します（下の例は0に非常に近い数値が出力されます）。
  ただ、ニュートン・ラフソン法は初期値が解の近傍にないと収束しないので注意してください。
  
  # sympy変数、展開する式の定義と関数実行
  x = Symbol(‘x’)
  f = x ** 3
  x1 = newton_raphson(f, x1=1)
  
  返信