
テイラー展開は任意点周りの近似計算をすることが出来るため、様々な工学的・物理的場面で活躍します。ここではsympyを使って面倒なテイラー展開をPythonにやらせ、グラフプロットまで自動で行うことを目標とします。
こんにちは。wat(@watlablog)です。ここではPython/sympyを使ってテイラー展開を自動で行ってプロットする所までをやってみます!
テイラー展開の式
Pythonのsympyでテイラー展開を計算する前に、まずは式の確認をしていきましょう。
このページでは\(f(x)\)と関数の変数が\(x\)とただ1つだけの場合を考えます。
任意点\(x=a\)周りのテイラー展開を式(1)で示します。
この式は一見すると複雑で難しい印象を受けます。
しかし、1次近似までを見ると高校で習う接線の公式になっていることに気付くと思います。
テイラー展開の目的は任意点の情報から近傍の状態を知る(近似する)ことにあります。
テイラー展開は接線の公式を延長し、2次、3次と無限次まで精度を高めると元の関数と一致するということを意味しています。複雑な式の意味も元の式を多項式で近似しているということですね。
sympyの使い方:テイラー展開を体験する
sympyとは?
sympyとは、記号(Symbol)を記号のまま数学的な処理をすることが可能なPythonライブラリです。
例えば、\(y=x^{2}\)を微分して値を求める場合、通常のプログラミングであればプログラマが\(y'=2x\)を記述し、そこに値を入れるか、近似的な計算手法を使って求めるかの2通りが考えられます。
しかしsympyを使えば\(x\)と\(y\)をSymbolとして定義し、プログラム的に\(y'=2x\)を求めることが可能です。近似的手法に頼ることなく解が得られる等の様々なメリットが考えられますね。
インストール
sympyはpipでインストールすることが可能です。Windowsであればコマンドプロンプトに以下のコードを打ち込むことでインストールが完了します。
|
1 |
python -m pip install sympy |
import文
import文の書き方は人により様々ですが、import*とアスタリスクを付けた形で書く人が多いかも知れません。 sympyはsinやcos, expといった関数はそれぞれimportすることも出来ますが、import*と書いておけば個別に書く必要がありません。
|
1 |
from sympy import* |
記号(シンボル)を定義する
sympyではこれから扱いたい\(x\)や\(y\)といった変数を以下のコードで示すようにSymbolを使って定義します。
|
1 2 |
# シンボルを定義 x = Symbol('x') |
テイラー展開を計算する
以下がテイラー展開を計算するコードです。指数関数\(f(x)=e^{x}\)を\(x=0\)点で第3項\(n=3\)まで展開しています(原点周りなので、正確にはマクローリン展開と呼びます)。
|
1 2 |
taylor = series(exp(x), x=x, x0=0, n=3) print(taylor) |
\(e^{x}\)をマクローリン展開すると、以下の式(2)となります(上の式(1)に当てはめて計算してみて下さい)。
\[
f(x)=1+x+\frac{1}{2}x^{2}+\cdots
\tag{2}
\]
上記コードを実行すると、以下の結果を得ます。式(2)と同じですね。
O()は剰余項を意味していて、nで指定した項以外がまとめられているものだそうです。
|
1 |
1 + x + x**2/2 + O(x**3) |
なんとなくsympyの使い方がわかってきました!それにしても、記号を処理してくれるのは地味にすごいですね!
ただ、これだけだと「計算結果を表示させてみました」に過ぎず、特に面白くありません。
そこで、以下にsympyで得られた式をnumpy形式で出力させ、matplotlibでグラフへプロットするということをやってみます。
sympyで自動テイラー展開してプロットをするコード
\(f(x)=e^{x}\)
以下のコードは\(e^{x}\)をseriesでテイラー展開し、計算された多項式をlambdifyを使ってnumpyの関数化させています。solは関数化させたオブジェクトtaylor_yに横軸cal_xを代入してnumpy形式で配列を得ています。
このコードではfor文を使ってn(項数)違い、つまり複数の精度違いで結果をプロットしています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
from sympy import* import numpy as np from matplotlib import pyplot as plt # 理想波形を生成 cal_x = np.arange(-10.0, 10.1, 0.1) cal_y = np.exp(cal_x) # シンボルを定義 x = Symbol('x') # 任意点周りのテイラー展開を精度違いで計算する sol = [] # 結果の入れ物 a = 0 # 任意点 for i in range(6): taylor = series(exp(x), x=x, x0=a, n=i+2).removeO() # removeO()で剰余項を除去する print(taylor) # 式を表示させて確認 taylor_y = lambdify(x, taylor, 'numpy') # numpyの関数に変換 sol.append(taylor_y(cal_x)) # 関数に値を入れて曲線を計算 # ここからグラフ描画--------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルとスケールを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_xlim(-2, 2) ax1.set_ylim(-2, 8) # データをプロットする。 ax1.plot(cal_x, cal_y, label='Theory', lw=3, color='black') for j in range(len(sol)): ax1.plot(cal_x, sol[j], label='Series:n=' + str(j+2)) fig.tight_layout() # グラフを表示する。 plt.legend() plt.show() plt.close() # --------------------------------------------------------------------- |
実際に値を入れて計算するには、removeO()で剰余項を外す必要がある所がキーポイントです。removeO()を付けないと以下のエラーが発生します。
NameError: name 'O' is not defined
以下は任意点\(a\)違いの結果を2つ例として比較しています。左が\(a=0\)点周りのマクローリン展開、右が\(a=1\)周りのテイラー展開の結果です。
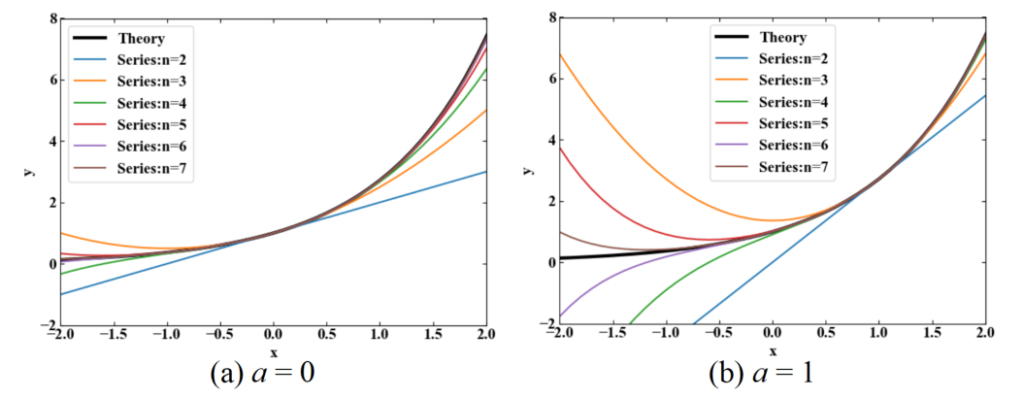
コード上で\(a\)の値を変えるだけで、\(a\)点周りの近似曲線を得ることが出来ました!
\(f(x)=\sin x\)
続いて\(\sin x\)もテイラー展開してみましょう。以下は上記expをsinに変更しただけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
from sympy import* import numpy as np from matplotlib import pyplot as plt # 理想波形を生成 cal_x = np.arange(-10.0, 10.1, 0.1) cal_y = np.sin(cal_x) # シンボルを定義 x = Symbol('x') # 任意点周りのテイラー展開を精度違いで計算する sol = [] # 結果の入れ物 a = 0 # 任意点 for i in range(6): taylor = series(sin(x), x=x, x0=a, n=2*(i+1)).removeO() # removeO()で剰余項を除去する print(taylor) # 式を表示させて確認 taylor_y = lambdify(x, taylor, 'numpy') # numpyの関数に変換 sol.append(taylor_y(cal_x)) # 関数に値を入れて曲線を計算 # ここからグラフ描画--------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルとスケールを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_xlim(-3, 3) ax1.set_ylim(-1.5, 1.5) # データをプロットする。 ax1.plot(cal_x, cal_y, label='Theory', lw=3, color='black') for j in range(len(sol)): ax1.plot(cal_x, sol[j], label='Series:n=' + str(j+2)) fig.tight_layout() # グラフを表示する。 plt.legend() plt.show() plt.close() # --------------------------------------------------------------------- |
結果は下図です。同じく\(a=0\)と\(a=1\)を比較してみました。同じように任意点周りの近似がされていることがわかりました。
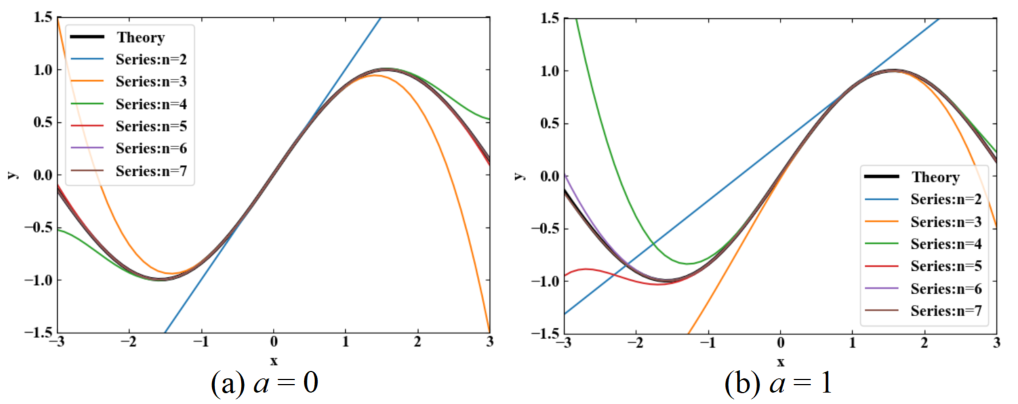
まとめ
本記事では\(f(x)\)のテイラー展開の概要を説明し、sympyの簡単なテイラー展開の使い方を紹介しました。
ただコンソール画面に展開結果を表示させるだけではなく、numpy形式としてグラフ化可能な曲線を得る方法も調査してみました。
sympyにも簡易プロッティング機能はあるそうですが、Python使いはnumpyとmatplotlibで出来た方が他の処理と連携しやすく有用でしょう。
最後にテイラー展開でよく例題として出される\(e^{x}\)と\(\sin x\)を実際にsympyで展開し、教科書でお馴染みの結果を得ることが出来ました。
テイラー展開を手計算でやらなくても良いというのは地味に画期的!?
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント