
コンピュータに連立方程式を計算させる時は、線形代数学で学んだ行列形式で方程式を表現する方が効率的です。ここではPythonをはじめ様々なコンピュータシミュレーションのために、多自由度振動系の運動方程式を行列形式へ変換する方法を紹介します。
こんにちは。wat(@watlablog)です。
本日はプログラミング要素はあまりありませんが、個人的に基礎的な部分も記しておきたいと思ったので、多自由度振動系の運動方程式を行列形式に変換する方法をまとめます!
多自由度振動系モデルの運動方程式立てる
作用している力を考えよう!
今回扱う多自由度振動系とは、以下に示すモデルを指します。このモデルは質点が2つあるので、2自由度を持つと言えます。
1自由度の場合は「Pythonで1自由度非減衰系の自由振動シミュレーション」で説明したように、非常に考えやすい式でした。しかし、このような複数の自由度を持つ場合でも考え方は同じです。
まずは質点に作用している力を考えましょう!
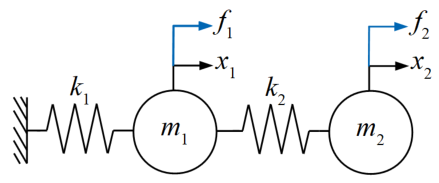
\(m_{1}\)に作用する力から\(m_{1}\)の運動方程式を立てる
運動方程式の基本は\(F=ma\)なので、左辺の力の合計を考えて、右辺の質量と加速度(これも慣性力という力)を考えます。
まずは質点\(m_{1}\)に作用する力ですが、質点自体にも力がかかる可能性があるため、\(f_{1}\)が挙げられますね。図の右方向を正とすればプラスの力です。
次に、\(m_{1}\)の左側にはばねがあるので、フックの法則からばねの伸びに比例して復元力が発生します。ばねの左端は固定点なので変位が発生せず、この復元力は\(x_{1}\)によってのみ発生します。但し、質点を左側に引っ張る方向に作用するので、力の符号は負となり\(-k_{1}x_{1}\)になります。
また、\(m_{1}\)の右側にもばねがあります。このばねに発生する復元力はフックの法則で考えると質点\(m_{1}\)と\(m_{2}\)の両方の相対変位\(x_{2}-x_{1}\)で決まるので\(k_{2}\left ( x_{2}-x_{1} \right )\)になります。
後は右辺の質量と加速度を加えてニュートンの運動方程式を立てると、式(1)が導出されます。
$$f_{1}-k_{1}x_{1}+k_{2}\left ( x_{2}-x_{1} \right )= m_{1}\ddot{x_{1}} (1)$$
式(1)において、左辺に力\(f_{1}\)だけを置き、その他を全て右辺に移項、\(x_{1}\)と\(x_{2}\)についてまとめると式(2)が得られます。これが質点\(m_{1}\)の運動方程式になります。
$$f_{1}=m_{1}\ddot{x}_{1}+\left(k_{1}+k_{2}\right)x_{1}-k_{2}x_{2} (2)$$
\(m_{2}\)に作用する力から\(m_{2}\)の運動方程式を立てる
では続いて質点\(m_{2}\)の運動方程式も求めてみましょう!
まずは左辺ですが、先ほどと同様に、\(m_{2}\)自体にも力がかかる可能性があるので\(f_{2}\)を正の方向で置きます。
そして質点\(m_{2}\)の左側にはばねがありますので、方向が負の復元力が働きます。このばねは\(x_{2}-x_{1}\)の相対変位で変位が決まり、ばね定数\(k_{2}\)をかけた\(-k_{2}\left ( x_{2}-x_{1} \right )\)が質点\(m_{2}\)に作用する復元力です。
質点\(m_{2}\)の右側は自由端となりもうばねは無いので、復元力は以上です。
式(1)と同様に右辺に質量と加速度をとると、式(3)が得られます。
$$f_{2}-k_{2}\left ( x_{2}-x_{1} \right )=m_{2}\ddot{x}_{2} (3)$$
この式(3)も式変形をして整理すると、式(4)を得ることができ、これが質点\(m_{2}\)の運動方程式になります。
$$f_{2}=m_{2}\ddot{x}_{2}-k_{2}x_{1}+k_{2}x_{2} (4)$$
連立方程式を行列表示させる
各質点における運動方程式が立てられたら、後は簡単です。まず式(2)と式(4)を一組にした連立方程式(5)を立てましょう。
\[
\begin{cases}
f_{1}=m_{1}\ddot{x}_{1}+\left(k_{1}+k_{2}\right)x_{1}-k_{2}x_{2}\\
f_{2}=m_{2}\ddot{x}_{2}-k_{2}x_{1}+k_{2}x_{2}
\end{cases} (5)
\]
このような連立方程式が出来上がったら、「Pythonで線形代数!連立1次方程式を解く」で実施したように行列形式で書くことができます。もし忘れてしまった方はこちらの記事を参照して頂きたいと思います。
式(6)に式(5)を行列表示させた式を示します。この式は線形代数の行列計算を行うことで式(5)に戻すことも可能です。
\[
\begin{bmatrix}
f_{1}\\
f_{2}\end{bmatrix}
=
\begin{bmatrix}
m_{1} &0 \\
0 &m_{2}
\end{bmatrix}
\begin{bmatrix}
\ddot{x}_{1}\\
\ddot{x}_{2}
\end{bmatrix}
+
\begin{bmatrix}
k_{1}+k_{2} &-k_{2} \\
-k_{2} &k_{2}
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2}
\end{bmatrix} (6)
\]
上の式(6)は成分をいちいち書いていると大変なので、式(7)と書くこともあります。ここで、\(\mathbf{F}\)は外力ベクトル、\(\mathbf{M}\)は質量マトリクス、\(\mathbf{K}\)は剛性マトリクス、\(\mathbf{\ddot{x}}, \mathbf{x}\)はそれぞれ加速度ベクトルと変位ベクトルと呼びます。
$$\mathbf{F}=\mathbf{M}\mathbf{\ddot{x}}+\mathbf{K}\mathbf{x} (7)$$
これで多自由度振動系の運動方程式を行列表示させる方法の説明は終了です。
基本はこの考え方で、ばねが並列になっていようが直列になっていようが、力の作用を考えて運動方程式を立てれば同じように整理することが可能です。
まとめ
本ページではこの後Pythonを使って振動の解析を行うために、まずは基礎知識として運動方程式を立てる方法を学びました。
多自由度の質点モデルは質点に作用する力とその方向を記述すれば運動方程式を作ることができます。
そして、運動方程式が連立する場合は行列表示にすることも、コンピュータで計算を行う場合は有効な手段です。
今回は特にコードを紹介することは無かったけど、この方程式を基本として様々な解析、分析を行っていくよ!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
いつも楽しく拝読させていただいております。もし可能でしたら、python3を使ってのコードを教えていただけないでしょうか。前の単振動の分を参考に作成しているのですが、どうも上手くいきません。何卒、よろしくお願いいたします。
ご訪問ありがとうございます!
本記事は「Pythonで多自由度系の固有値解析!固有振動数とモードを計算」の前段階として書きましたが、
Pythonコードで実現したい内容としては、固有値解析ではなく、時刻歴応答解析がしたいという理解でよろしいでしょうか?
お忙しい中、返信いただきどうもありがとうございます。
仰るとおり時刻歴応答解析です。
先の記事でありました”Pythonで1自由度非減衰系の自由振動シミュレーション”にあるグラフを模して作ろうとしておりますが、どうもうまく行きません。python3の初学者であり、非常に苦労しております。もしよければご教授いただけますと幸いに思います。
何卒、よろしくお願いいたします。
承知致しました。
実は僕も以前pythonのodeintを使って行列形式の微分方程式の時刻歴応答シミュレーションをトライしましたが、ライブラリを行列に対応させる方法がわからず保留していました。
他の方法(Runge-Kutta等)も視野に入れつつ再度トライしたいと思います。
しかし3月に機械学習系の試験がありそちらに時間を少し割きます。簡単に出来ない場合は少しお時間を頂くことになると思います…。
もしお急ぎであればこのブログの更新を待たずに調べた方がよいかもしれません…。
とはいえ、次のシミュレーションカテゴリの記事はこの内容にしようと思いますので、よろしくお願い致します!
承知いたしました。私もそのあたりで苦労しております。
こちらも調べながら解決してみたいと思います。
どうぞ、よろしくお願いいたします。
遅くなったので既に解決されているかも知れませんが、
「https://watlab-blog.com/2020/02/17/runge-kutta4-vibration/」
という記事に多自由度振動系の時間応答シミュレーションコードを書いてみました。
scipyのodeintがもっと理解できれば良かったのですが、少々時間がかかりそうでしたのでまずは世間一般で利用されているRunge-Kutta法を試してみました。
scipyを使って計算が出来るようになればまた別途記事を作成しようと思います。
もし本記事でご不明点等ございましたら、いつでもお気軽にコメント頂ければと思います。
以上、よろしくお願い致します!
お忙しい中、大変ありがとうございます。もう出来ていたとは大変驚きました。
私の方でも使わせていただきました感想について、リンク先にも書かせていただきましたが、ここまでできておりましたら大満足です。
引き続き、wat様のブログで勉強させていただきます。
今後ともよろしくお願いいたします。
こちらにもご返信ありがとうございます!
これからも記事をお楽しみいただけると幸いです。
よろしくお願い致します。