Pythonで1自由度減衰系の強制振動シミュレーション

自由振動の後は強制振動を学びます。基本を学ぶためまずは1自由度の質点に周期加振力が働く場合の振動をPythonでコーディングしてみます。

こんにちは。wat(@watlablog)です。
1自由度の自由振動を習得した後は強制振動を習得します。基礎が大事なので、こちらも1自由度でコーディングしていきます！

目次（項目クリックでジャンプできます）

強制振動とは？

モデル

強制振動とは、前回までに学んだ自由振動と異なり、外部から強制的に力が供給され、質点が振動させられる状況のことを言います。

以下は1自由度減衰系のモデルに周期外力$F$が作用した状態を表した図です。

強制的に外力が働くといっても、モデルにはばねとダンパーが付いているので、単純に外力の信号によってのみで動くわけではなく、自身の復元力や抵抗力も作用するため、これまでと同様に運動方程式を立てて見ていきましょう。

運動方程式

今回対象とする上記モデルの運動方程式を式(1)に示します。周期加振としては何でも良いのですが、このページでは正弦波信号の形を取りました。

$$m\ddot{x}+c\dot{x}+kx= Asin(2\pi f t) (1)$$

コードを載せる前に、Pythonで常微分方程式を解くための前段階である変数変換をしておきましょう。

変数変換は式(2)で実施し、式(1)に代入して式(3)を得ます。

\[ \begin{cases}
x_{1}= x \\
x_{2}= \dot{x}
\end{cases}　(2)
\]

$$\dot{x_{2}}= Asin(2\pi f t)-\frac{c}{m}x_{2}-\frac{k}{m}x_{1}　(3)$$

Pythonによるコーディング

全コード

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# mkc force system
def func(state,t, m, k, c, A, f):
    x1, x2 = state
    dx2dt = - (c/m) * x2 - (k/m) * x1 + A * np.cos(2*np.pi*f*t)
    return [x2, dx2dt]

m = 0.5                         # 質量[kg]
k = 1000                        # 剛性[N/m]
c = 5                           # 減衰係数[N・s/m]
A = 100                         # 強制外力の振幅[N]
f = [1, 7, 20]                  # 強制外力の周波数[Hz]
state0 = [0.0, 0.0]             # 初期値[x0, v0]

t0 = 0                          # 初期時間[s]
tf = 10                         # 終了時間[s]
dt = 0.005                      # 時間刻み[s]
t = np.arange(t0, tf+dt, dt)    # 時間軸配列


# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Displacement [m]')

# データの範囲と刻み目盛を明示する。
ax1.set_xticks(np.arange(0, 10, 0.5))
ax1.set_yticks(np.arange(-1, 1, 0.1))
ax1.set_xlim(0, 2)
ax1.set_ylim(-0.3, 0.3)

# データプロット
labeling = ["f = 1[Hz]", "f = 7[Hz]", "f = 20[Hz]"]

for i in range(3):
    sol = odeint(func, state0, t, args=(m, k, c, A, f[i]))
    ax1.plot(t, sol[:, 0], label=labeling[i])

fig.tight_layout()
plt.legend(loc='upper right')

# グラフを表示する。
plt.show()
plt.close()

import numpy as np

from scipy.integrate import odeint

import matplotlib.pyplot as plt

# mkc force system

def func(state,t, m, k, c, A, f):

x1, x2 = state

dx2dt = - (c/m) * x2 - (k/m) * x1 + A * np.cos(2*np.pi*f*t)

return [x2, dx2dt]

m = 0.5 # 質量[kg]

k = 1000 # 剛性[N/m]

c = 5 # 減衰係数[N・s/m]

A = 100 # 強制外力の振幅[N]

f = [1, 7, 20] # 強制外力の周波数[Hz]

state0 = [0.0, 0.0] # 初期値[x0, v0]

t0 = 0 # 初期時間[s]

tf = 10 # 終了時間[s]

dt = 0.005 # 時間刻み[s]

t = np.arange(t0, tf+dt, dt) # 時間軸配列

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('Displacement [m]')

# データの範囲と刻み目盛を明示する。

ax1.set_xticks(np.arange(0, 10, 0.5))

ax1.set_yticks(np.arange(-1, 1, 0.1))

ax1.set_xlim(0, 2)

ax1.set_ylim(-0.3, 0.3)

# データプロット

labeling = ["f = 1[Hz]", "f = 7[Hz]", "f = 20[Hz]"]

for i in range(3):

sol = odeint(func, state0, t, args=(m, k, c, A, f[i]))

ax1.plot(t, sol[:, 0], label=labeling[i])

fig.tight_layout()

plt.legend(loc='upper right')

# グラフを表示する。

plt.show()

plt.close()

実行結果

以下の図が実行結果です。結果は1[Hz]よりも7[Hz]の方が質点の変位振幅が大きく、20[Hz]はそれらよりも小さいということが得られました。

というのも、この$m, k$の組み合わせは7[Hz]付近に固有振動数を持つので、共振が発生して変位振幅が大きくなったと言うことが出来ます

このモデルは減衰を含む系なので、共振が発生しても無限大の振幅にはなりません。

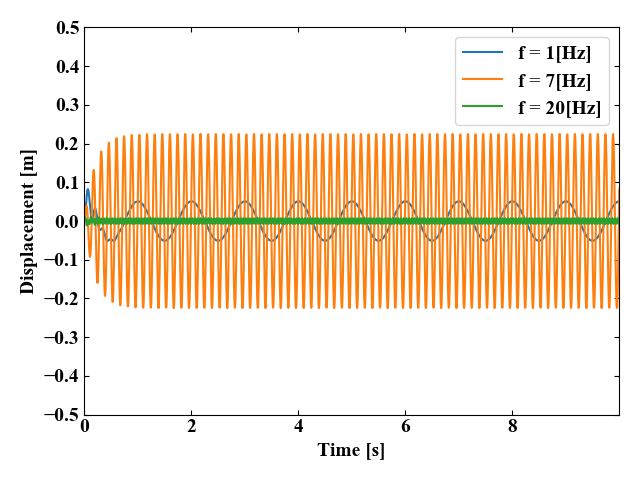
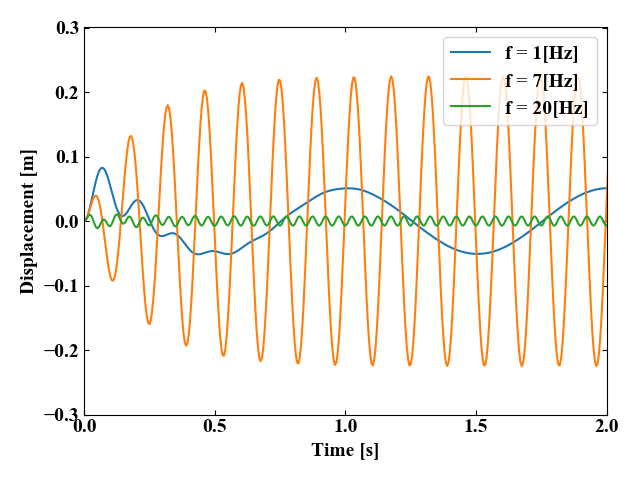
ではさらに初期時間の方を拡大して見てみましょう。

計算を始めた初期は、特に1[Hz]の波形で顕著ですが、固有振動数の周期で細かい波が発生している様子が見れました。ここでは取り扱いませんが、強制振動の解は自由振動の解を使って特解を出すので、その影響が出ているものと考えられます。この初期の変化が大きい部分の振動を過渡振動、安定した時の振動を定常振動と呼びます。

まとめ

本ページでは強制振動が働く1自由度減衰系のモデルを示し、運動方程式を紹介しました。

運動方程式は2階線形常微分方程式なので、Pythonでシミュレーションをするために、変数変換を利用して1階の常微分方程式に変換しました。

変換された式を関数にし、Pythonのodeintによるシミュレーションを行い、固有振動数前後の影響や過渡振動を観察しました。

強制振動も自由振動と同じでPythonを使えば簡単に数値解を得ることができました！

Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

強制振動とは？

モデル

運動方程式

Pythonによるコーディング

全コード

実行結果

まとめ

コメント

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

強制振動とは？

モデル

運動方程式

Pythonによるコーディング

全コード

実行結果

まとめ

SNSでもご購読できます。

コメント

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル