
Pythonを使うと簡単にFFTやスペクトログラムを計算できますが、より深い分析を行う場合は任意の帯域(バンド)毎に統計量や技術計算をかける場合があります。ここでは、Pythonで得られたスペクトルからバンド計算をする方法を紹介します。
こんにちは。wat(@watlablog)です。ここではFFTやスペクトログラムからバンド毎の計算を行うTipsを紹介します!
バンド計算の概要
FFTとスペクトログラムのおさらい
これからFFTやスペクトログラムからバンド計算を行う方法について記載しますが、そもそも「FFTとは?」「スペクトログラムって?」という方は是非以下の記事をまず読んでみて下さい。
「PythonでFFT実装!SciPyのフーリエ変換まとめ」
「Pythonで音のSTFT計算を自作!スペクトログラム表示する方法」
バンド計算とは?
バンド計算を説明する前に、まずは上記FFTから得られる情報をみてみましょう。
時間波形に対しFFTをかけると、以下のような周波数波形(ここでは振幅を例にしています)を得ます。この波形を見ると、まず目に入ってくるのは図中に示したピークの情報です。
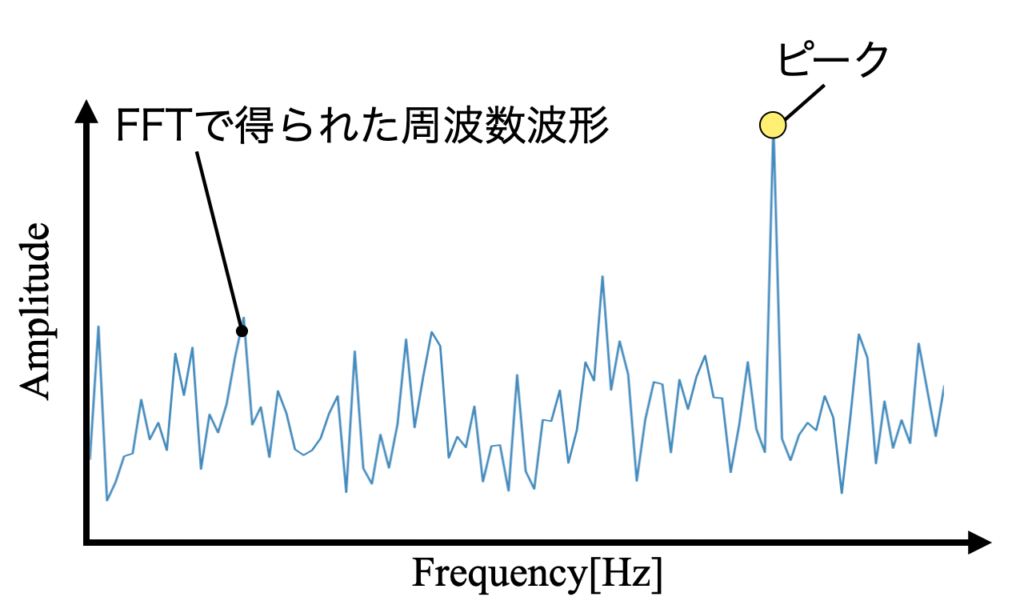
ピークの値を定量的に求める場合は「PythonでFFT波形から任意個数のピークを自動検出する方法」で紹介した方法があります。
しかし、単純にピークの値を知りたいわけではなく、○[Hz]-○[Hz]の範囲の統計量(平均・分散・標準偏差等)を知りたい時もよくあります。
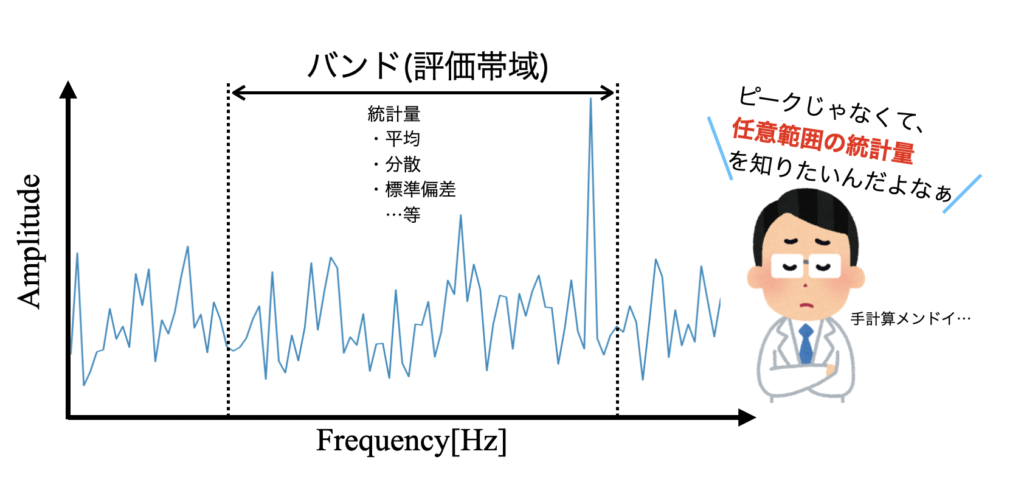
この周波数領域の任意範囲というのがバンド(Band:帯域)と呼ばれるものです。統計量の他に音や振動の場合は全バンドのオーバーオール値や部分バンドのパーシャルオーバーオール値といった振幅レベルの指標を求めるというのも、製品開発の中では頻繁に行われています。
この記事ではバンド毎の計算を行う事をバンド計算と呼んでいますが、特に一般用語ではないと思われるので使用の際はご注意下さい。
ちなみに、スペクトログラムに対して任意のバンドを設定して統計量を計算すると、下図のような時間によって統計量が変化する結果を得ます。
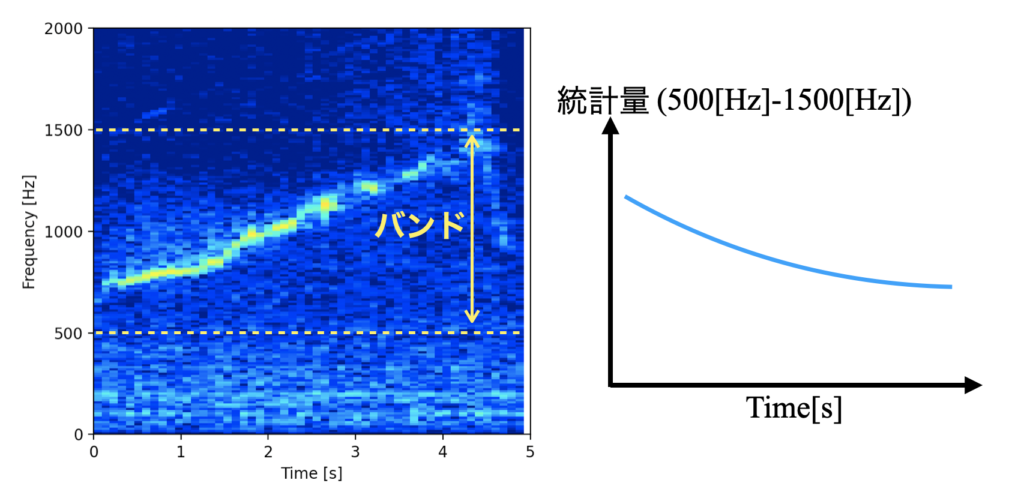
今回はこれらのバンド計算を書いていきます!
Pythonでバンド計算をするコード
FFT波形の場合
まずは基本としてFFT波形の場合です。FFT波形は1Dの配列なので、Numpyのスライスを用いて周波数範囲を指定して計算に使用するデータ(extracted)を抽出しています。
この時、周波数[Hz]を指標(何番目のデータか)に変換する計算を入れている事に注意して下さい。
以下のコードでは平均と標準偏差を計算してコンソールに表示、さらにグラフ上に抽出した結果と計算結果を描画しています。
基本は「PythonでFFT実装!SciPyのフーリエ変換まとめ」の1フレームフーリエ変換と同じですので、是非こちらの記事もご覧下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt # FFTをする関数 def fft_ave(data, samplerate, Fs): fft = fftpack.fft(data) # FFT(実部と虚部) fft_amp = np.abs(fft / (Fs / 2)) # 振幅成分を計算 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 return fft, fft_amp, fft_axis # サンプルの時間領域信号を生成 dt = 0.001 t = np.arange(0, 1, dt) noise = np.random.normal(loc=0, scale=1, size=len(t)) wave = 1 * np.sin(2 * np.pi * 20 * t) +\ 2 * np.sin(2 * np.pi * 40 * t) +\ 3 * np.sin(2 * np.pi * 60 * t) +\ 4 * np.sin(2 * np.pi * 80 * t) + 15 * noise # FFT fft, fft_amp, fft_axis = fft_ave(wave, 1 / dt, len(wave)) # 統計量の計算 fl = 10 # 低域カットオフ周波数 fh = 20 # 高域カットオフ周波数 df = fft_axis[1] # 周波数分解能 fl_i = int(fl / df) # flの指標(Numpyスライス用) fh_i = int(fh / df) # fhの指標(Numpyスライス用) extracted = fft_amp[fl_i:fh_i] # FFT波形の振幅からデータを抽出 mean = np.mean(extracted) # 平均を計算 std = np.std(extracted, ddof=1) # 不偏標準偏差 print('Mean=', mean) print('σ=', std) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Frequency [Hz]') ax1.set_ylabel('y') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 1 / dt, 20)) ax1.set_xlim(0, 100) ax1.set_ylim(0, 5) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(fft_axis, fft_amp, label='fft_amp', lw=1) ax1.plot(fft_axis[fl_i:fh_i], extracted, label='extracted', lw=3) # バンドで補助線を引いて結果をテキストで描画する。 plt.vlines([fl_i], -10, 10, "blue", linestyles='dashed') plt.vlines([fh_i], -10, 10, "blue", linestyles='dashed') plt.text(fh_i+1, max(extracted)+1, 'mean=' + str(round(mean, 2)), fontsize=20) plt.text(fh_i+1, max(extracted)+0.5, 'std=' + str(round(std, 2)), fontsize=20) fig.tight_layout() plt.legend() # グラフを表示する。 plt.show() plt.close() |
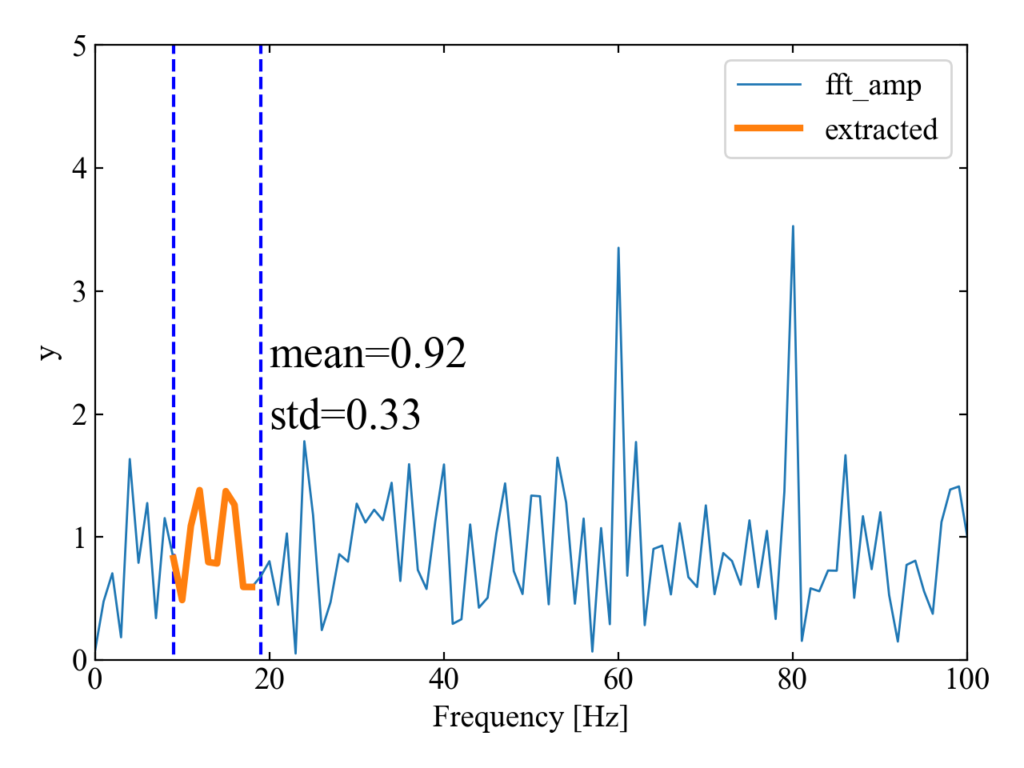
意図した部分が抽出できており、統計量を計算する事ができました。ちなみにここで算出している標準偏差は不偏標準偏差です。Numpyデフォルトだと母標準偏差のようですが、Pandasデフォルトに合わせました。
以下の図は10[Hz]から20[Hz]までのデータで計算をしています。
スペクトログラムの場合
次はスペクトログラムの例です。スペクトログラムは2Dデータですが、やっている事は先ほどの1Dデータと変わらずNumpyのスライスをしているだけです。
calc_spec_band()関数がスペクトログラムからバンド計算をする部分です。
プロット部分等少しいじっていますが、基本のコードは「PythonでFFT波形から任意個数のピークを自動検出する方法」とほぼ同じなので、詳細はこちらを参考にして下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 |
import numpy as np from scipy import signal from scipy import fftpack import soundfile as sf from matplotlib import pyplot as plt # スペクトログラムのバンド計算(平均と標準偏差)をする関数 def calc_spec_band(fft_array, fft_axis, fl, fh): df = fft_axis[1] # 周波数分解能 fl_i = int(fl / df) # flの指標(Numpyスライス用) fh_i = int(fh / df) # fhの指標(Numpyスライス用) # 計算結果の入れ物を初期化 means = np.zeros(len(fft_array)) stds = np.zeros(len(fft_array)) peaks = np.zeros(len(fft_array)) # スペクトログラムを時間方向に走査しながら統計量を計算 for i in range(len(fft_array)): extracted = fft_array[i][fl_i:fh_i] # FFT波形の振幅からデータを抽出 means[i] = np.mean(extracted) # 平均を計算 stds[i] = np.std(extracted, ddof=1) # 不偏標準偏差 peaks[i] = np.max(extracted) # 最大値 return means, stds, peaks # オーバーラップをかける関数 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数(平均化に使うデータ個数) array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 final_time = (ps + Fs)/samplerate # 切り出したデータの最終時刻 return array, N_ave, final_time # オーバーラップ抽出されたデータ配列とデータ個数、最終時間を戻り値にする # ハニング窓をかける関数(振幅補正係数計算付き) def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf # dB(デシベル)演算する関数 def db(x, dBref): y = 20 * np.log10(x / dBref) # 変換式 return y # dB値を返す # 聴感補正(A補正)する関数 def aweightings(f): if f[0] == 0: f[0] = 1 ra = (np.power(12194, 2) * np.power(f, 4))/\ ((np.power(f, 2) + np.power(20.6, 2)) * np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * (np.power(f, 2) + np.power(737.9, 2))) * (np.power(f, 2) + np.power(12194, 2))) a = 20 * np.log10(ra) + 2.00 return a # 平均化FFTする関数 def fft_ave(data_array, samplerate, Fs, N_ave, acf): fft_array = [] fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 a_scale = aweightings(fft_axis) # 聴感補正曲線を計算 # FFTをして配列にdBで追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 for i in range(N_ave): fft_array.append(db (acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2)) , 2e-5)) fft_array = np.array(fft_array) + a_scale # 型をndarrayに変換しA特性をかける fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis path = 'sample.wav' #ファイルパスを指定 data, samplerate = sf.read(path) #wavファイルを読み込む x = np.arange(0, len(data)) / samplerate #波形生成のための時間軸の作成 # Fsとoverlapでスペクトログラムの分解能を調整する。 Fs = 4096 # フレームサイズ overlap = 0 # オーバーラップ率 # オーバーラップ抽出された時間波形配列 time_array, N_ave, final_time = ov(data, samplerate, Fs, overlap) # ハニング窓関数をかける time_array, acf = hanning(time_array, Fs, N_ave) # FFTをかける fft_array, fft_mean, fft_axis = fft_ave(time_array, samplerate, Fs, N_ave, acf) # スペクトログラムの時間分解能を計算する spec_dt = final_time / N_ave # スペクトログラムの統計量を計算 means, stds, peaks = calc_spec_band(fft_array, fft_axis, fl=500, fh=1500) time_axis = np.arange(0, final_time, spec_dt) # スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置 fft_array = fft_array.T # ここからグラフ描画 # グラフをオブジェクト指向で作成する。 fig = plt.figure(figsize=(10,3)) ax1 = fig.add_subplot(121) ax2 = fig.add_subplot(122) # データをプロットする。 ax1.plot(time_axis, means, label='mean') ax1.plot(time_axis, stds, label='std') ax1.plot(time_axis, peaks, label='peak') ax1.text(1, 80, 'fl=500[Hz], fh=1500[Hhz]', fontsize=8) ax1.legend() im = ax2.imshow(fft_array, vmin=0, vmax=80, extent=[0, final_time, 0, samplerate], aspect='auto', cmap='jet') # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('SPL [dBA]') # 軸設定する。 ax2.set_xlabel('Time [s]') ax2.set_ylabel('Frequency [Hz]') # スケールの設定をする。 ax2.set_xticks(np.arange(0, 50, 1)) ax2.set_yticks(np.arange(0, 20000, 500)) ax2.set_xlim(0, 5) ax2.set_ylim(0, 2000) # グラフを表示する。 plt.show() plt.close() |
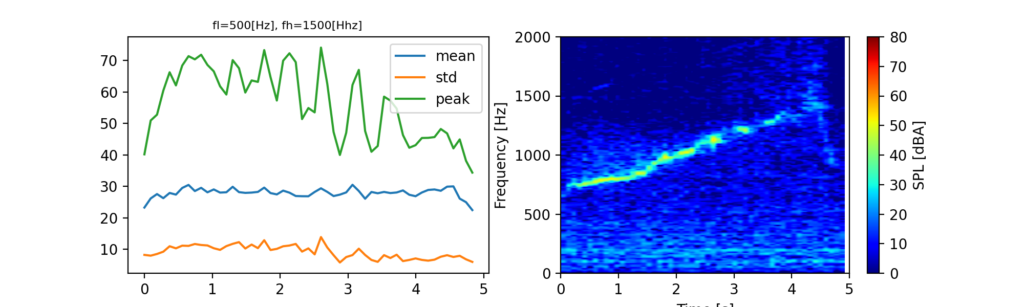
以下が結果です。左のグラフは500[Hz]から1500[Hz]の平均、不偏標準偏差、ピーク値をプロットしています。
スペクトログラムならではの時間変化を確認する事ができました。
まとめ
本記事ではFFTとスペクトログラムのおさらいを行い、バンド計算の概要を説明しました。
そして1Dと2Dのデータに対してバンド計算を行うPythonコードを紹介しました。
結果、単純にピークを検出する以上の情報をそれぞれの結果から得ることができました。
今回は短いTipsでしたが、是非Pythonによる信号処理をお楽しみ下さい。
バンド計算は簡単だけど有用な情報が沢山です!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
図が分かりやすくいつもありがとうございます!!バンド毎の分析で参考にさせていただいています。
例えば、10[Hz]から20[Hz]の積分値や、全体に占める10[Hz]から20[Hz]の積分値の割合はどのように計算すればよいでしょうか。
いつもご訪問ありがとうございます。
例えばスペクトログラムのコードをそのまま使えば、
extracted = fft_array[i][fl_i:fh_i]
で10[Hz]から20[Hz]を抽出することは可能です。
その後、means[i] = np.mean(extracted)等の代わりに、
積分の演算を行えば可能と思います。
単純な離散データの合算であればnp.sum()を使えば良いと思いますが、
ある程度正確な積分を行う場合はscipy.integrateでSimpson則やRomberg則による積分を行うのも良いかも知れません。
全体の積分は周波数バンドを抽出する前のfft_array[i]を使って計算すれば良いと思いますので、
forループの外で計算して最後に比を取れば目的の演算ができると思います。
積分演算は周波数波形の演算でよく使われるオーバーオールという計算につながりますので、
そのうちこのブログでも記事にしたいですが、まずは上記方針でご検討頂ければと思います!