
Pythonで時間波形に対してFFT(高速フーリエ変換)を行うことで周波数領域の分析が出来ます。さらに逆高速フーリエ変換(IFFT)をすることで時間波形を復元することも可能です。ここではPythonによるFFTとIFFTを行うプログラムを紹介します。
こんにちは。wat(@watlablog)です。
時間領域と周波数領域を自由に行き来しましょう!ここではPythonによるFFTとIFFTで色々な信号を変換してみます!
時間領域と周波数領域を理解しよう!
FFTとIFFTの関係
いきなりコードを紹介する前に、これから書くプログラムのイメージを掴んでおきましょう。
以下の図はFFT(Fast Fourier Transform:高速フーリエ変換)とIFFT(Inverse Fast Fourier Transform:逆高速フーリエ変換)の関係性を説明している図です。

時間波形と周波数波形はそれぞれ周波数、振幅(ここには書いてありませんが位相も)といった波を表す成分でそれぞれ変換が可能です。
以下のような複雑な波形でも同様に、FFTとIFFTの関係は成立します。上の簡単な波形はわざわざプログラムを使って変換処理をしなくてもひと目で波の形と成分はわかりますが、複雑になればなるほどコンピュータの力を借りたいものですね。
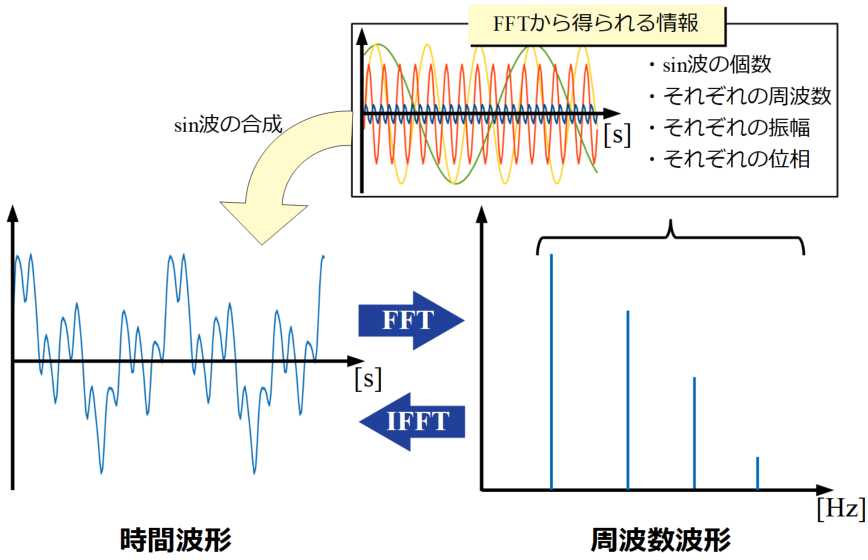
今回はこの図にあるような時間領域と周波数領域を自由に行き来できるようなプログラムを作ることを目標とします!
FFTとIFFTで出来ること2選
FFTは時間波形の周波数分析に使うから色々便利だけど、IFFTはなんのために使うものなんだ?
…と思うのは自然な感覚だと思います。ここでは一般にFFTとIFFTでどんなことが行われているのか、主に2つの内容を説明します。
①ノイズ成分を除去することができる
FFTとIFFTを併用すれば、信号のノイズ成分を除去することができます。
複雑な波形の場合、FFTをする前はノイズがどんなものかわからない場合があります。
例えば、ある周波数から上にしかノイズが含まれていない時は「PythonのSciPyでローパスフィルタをかける!」で紹介したように、ローパスフィルタによってノイズ除去が可能です。
その効果は以下の図を見れば明らかで、ローパスフィルタによって高周波ノイズをカットすることは容易にできます。
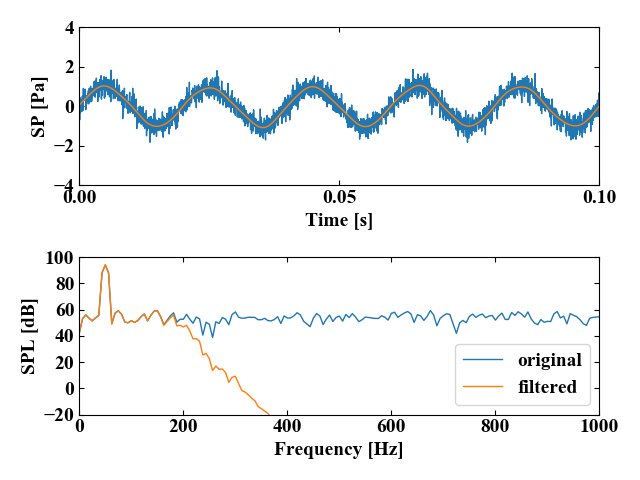
しかし、ノイズとは高周波帯域に一様に分布しているもの以外にも様々な種類があります。
その良い例が電源ノイズですが、測定系の中でGNDの取り方が悪かったりするとその地域の電源周波数(日本の関東なら50Hz)の倍数で次数が卓越します。
測定したい主信号がこの周波数と重なってしまうと取り切るのはかなり難しくなりますが、運良くずれている場合はIFFTで除去可能です。
時間領域の信号をFFTで周波数領域に変換し、周波数領域で特定のノイズ周波数を減衰させた後にIFFTで再び時間領域に戻すという手順でノイズ除去が可能です。
②時間波形の特定の周波数成分を増減できる
IFFTの効果は何もノイズ除去だけではありません。
FFT後の周波数領域で波形の編集ができ、IFFTで再び時間領域に戻すことができるという事は、イコライザが自作できるということです。
イコライザは音楽の分野で当たり前のように行われている技術ですが、やっていることは周波数帯域毎に振幅成分を増減させているだけです。
Pythonを使って自分でイコライザを作ることができれば、市販のソフトではできない細かいチューニングも思いのままですね!
後で作ってみよう!
PythonによるFFTとIFFTのコード
全コード
以下にサンプル波形である正弦波(振幅\(A\)=1、周波数\(f\)=20Hz)をFFTし、IFFTで元の時間波形を求める全コードを示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt # FFTをする関数 def fft_ave(data, samplerate, Fs): fft = fftpack.fft(data) # FFT(実部と虚部) fft_amp = np.abs(fft / (Fs / 2)) # 振幅成分を計算 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 return fft, fft_amp, fft_axis # サンプルの時間領域信号を生成 dt = 0.001 t = np.arange(0, 1, dt) wave = np.sin(2 * np.pi * 20 * t) # FFTとIFFT処理 fft, fft_amp, fft_axis = fft_ave(wave, 1 / dt, len(wave)) ifft_time = fftpack.ifft(fft) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Frequency [Hz]') ax1.set_ylabel('y') ax2.set_xlabel('Time [s]') ax2.set_ylabel('y') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 1 / dt, 20)) ax1.set_yticks(np.arange(0, 3, 0.5)) ax1.set_xlim(0, 100) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(fft_axis, fft_amp, label='signal', lw=1) ax2.plot(t, wave, label='original', lw=5) ax2.plot(t, ifft_time.real, label='ifft', lw=1) fig.tight_layout() plt.legend() # グラフを表示する。 plt.show() plt.close() |
importはNumPy, SciPy, matplotlibというシンプルなものです。グラフ表示部分のコードが長いですが、FFTとIFFTの部分はそれぞれ数行ほどなので、Pythonで簡単に計算ができるということがよくわかりますね。
以前WATLABブログでFFTを紹介した記事「PythonでFFT!SciPyのFFTまとめ」では、実際の実験での使用を考慮し、オーバーラップ処理、窓関数処理、平均化処理を入れていたためかなり複雑そうに見えましたが、今回は単純な信号の確認程度なので、FFTではそれらを考慮していません。
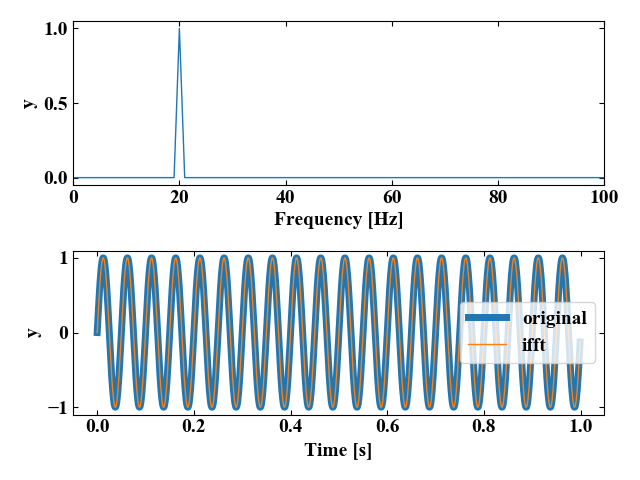
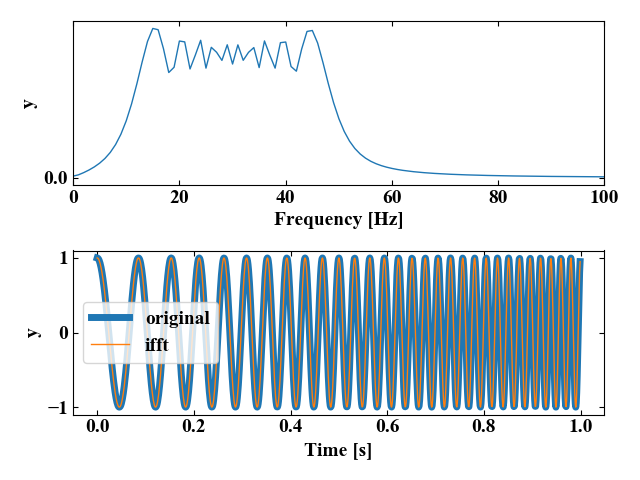
実行結果(正弦波)
以下の図は上のグラフがFFT波形、下のグラフが時間波形を示しています。時間波形には、元の波形(original)とIFFT後の波形(ifft)を重ねていますが、見事に一致している結果を得ることができました。
実行結果(振幅変調正弦波)
波形の種類を変えてテストしてみましょう。
次は振幅変調正弦波でFFTとIFFTを実行してみます。
振幅変調とは、波の振幅成分が時間によって変動する波形のことを意味します。
今回は以下のコードで正弦波を基に振幅変調をさせました。
上記全コードの波形生成部分を変更しただけとなります。
|
1 2 3 4 5 |
# サンプルの時間領域信号を生成 dt = 0.001 t = np.arange(0, 1, dt) wave = np.sin(2 * np.pi * 20 * t) wave *= (1 + 0.5 * np.sin(2 * np.pi * 2 * t)) |
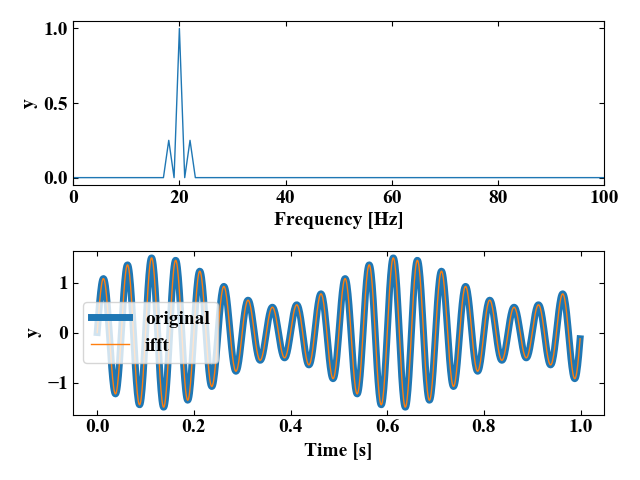
以下の図が実行結果です。
振幅変調があると、FFT波形にはサイドバンドとよばれる主要ピークの両端にある比で現れる小さなピークが発生しますが、今回の実行結果にも綺麗にサイドバンドが発生していますね。
IFFTの結果は今回も元波形と一致しました。
実行結果(チャープ信号)
最後はチャープ信号の場合です。チャープ信号は「Pythonでチャープ信号!周波数スイープ正弦波の作り方」で紹介していますが、時間により周波数が変化する波形です。
先ほどと同じように、波形生成部分を以下のコードに置き換えることでプログラムが動作します。
|
1 2 3 4 5 6 |
from scipy.signal import chirp # サンプルの時間領域信号を生成 dt = 0.001 t = np.arange(0, 1, dt) wave = chirp(t, f0=10, f1=50, t1=1, method='linear') |
以下が実行結果です。
周波数が10[Hz]から50[Hz]までスイープアップしているので、FFT結果はその範囲にピークが現れています(もっとゆっくりスイープさせ十分な時間で解析をすると平になります)。
IFFTの結果はこれまでと同様に、元波形と一致していることがわかりました。
まとめ
本記事では時間領域と周波数領域に関する理解のおさらいと、IFFT(逆高速フーリエ変換)で何ができるかを説明しました。
また、FFTとIFFTを様々な時間関数に対して実行し、周波数領域から復元された時間波形が元の時間波形と一致することを確かめました。
Pythonでできる信号処理技術がまた増えました!FFTと対をなすIFFTを覚えることで、今後色々な解析に応用ができそうだね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
こんにちは。
信号処理でノイズ除去する方法を模索中で、当ページを見つけ、大変参考にさせていただいています。
このページで逆フーリエ変換すると、確かに元の時間波形になるのは確認できました。
しかし、別ページで紹介されていた、「オーバーラップ処理をしてから平均化FFT」をして出てきた周波数波形をIFFTしても、元の時間波形と全く似て非なる波形になってしまいます。
その理由と、そうならないようにする方法を教えて頂けますでしょうか?
ご訪問、記事を参考にして頂きありがとうございます。
このページのIFFTでは、「負の周波数成分も全て含んだフーリエスペクトル」を使っています。
一方、平均化FFTの記事ではナイキスト周波数でデータを切り捨てており、この部分が理由で時間波形が再現できなくなります。
平均化FFTのコードでフーリエスペクトル(複素数)を計算している「fftpack.fft(data_array[i]」をそのまま(絶対値も何も計算しない)使ってIFFTをかけることが解決法となります。
そのためには「def fft_ave」間数でフーリエスペクトルを別途保持しておくか、振幅の計算だけ別の場所で行うか、色々な書き方があると思います。
(平均化フーリエスペクトルを作る。。とか)
負の周波数やナイキスト周波数についてはこちらを参考。
「https://watlab-blog.com/2019/04/21/python-fft/」
また、その他のIFFT関連の記事として、こちらのヒルベルト変換の記事も参考になるかも知れません。
IFFTする直前に簡単な演算をしているため、どのようなデータがIFFTに必要か…という部分をご参考にしてください。
「https://watlab-blog.com/2019/10/13/hilbert-envelope/」
面白そうなので近いうち当ブログでも記事化したいと思いました。
ただ時間はかかりそうなので、是非Tukさんの方でも挑戦してみてください。
以上、よろしくお願いいたします。
早速回答をありがとうございます。理由として回答くださった「ナイキスト周波数」なのですが、1点疑問が浮かび上がりました。
また、最初の質問において「このページで逆フーリエ変換すると」と言ってしまっていましたが、正確には誤りで、
下記のページ(URL①)に掲載のコードを参考に逆フーリエ変換していました。
① https://watlab-blog.com/2021/11/14/csv-idft/
逆フーリエ変換の対象ファイルは、以下(URL②)のおまけで紹介されているコードを用いて、
signals_2.csvに対して平均化FFTを実行した結果のファイルです。
② https://watlab-blog.com/2021/04/17/csv-dft/
signals_2.csvファイルに対して、URL②に記載の「単純なFFT」を実行し、その結果ファイルに対してURL①に記載のIFFTを実行すると、確かにもとのsignals_2.csvの波形と一致しますが、この場合でもナイキスト周波数でデータの切り捨て操作をしています。
そのため、なぜ平均化FFTをした後にそれを時間波形に戻そうとしても、元の波形と一致しないか、よく理解できません。
先日は誤った内容の質問をしてしまい大変申し訳ないのですが、よろしくお願いします。
なるほど。確かにナイキスト周波数だけが原因ではなさそうです。
まだこちらでは確認していませんが、平均化フーリエ変換の場合はフレームサイズをユーザーが指定している点が1フレームフーリエ変換との違いです。
平均化フーリエ変換は主にノイズを含んだ長時間の時間波形を適当なデータポイント数に分割して、あたかも不確かなノイズ成分の影響が少なかったかの結果を出します。
ただし、フレームサイズが理想的な周期で区切られていれば問題ないですが、適当なフレームで区切っても問題が少ないようにハニング窓をかけたりオーバーラップをかけたりしています。
すると毎フレームで位相情報の平均化がうまくいかないという可能性もありそうです。
ちょっとこちらでは確認できていませんが、1フレーム毎にフーリエ変換後のスペクトルを用いて逆フーリエ変換すると(ハニング窓やdB変換はせずに)、フレーム毎の時間波形は一致するかも知れませんね。
このような仮定を立てて検証すると原因の特定ができそうです。
Tuk様の現在のコードで検証可能でしょうか?
いつもご丁寧にありがとうございます。
教えていただいた通り、1フレームごとにフーリエ変換を行った後逆フーリエ変換すると、波形は一致しました。位相情報の平均化や、フレームの区切り方に注意しないといけないと考えられますので、こちらでも検証を続けてまいります。
ご報告や検証ありがとうございます。
どうやらそんなに簡単ではないようですね。。
こちらも検証不足の内容だったので質問助かりました。