
これまで当ブログでは2Dの「移流方程式」と「拡散方程式」を扱いました。ここではこれら2つの流体現象を組み合わせた「移流拡散方程式」を学びます。いつも通りPythonでコーディングしながら解説を行い、流れを確認して理解を深めます。
こんにちは。wat(@watlablog)です。今回はPythonで移流拡散方程式を学びます!
移流現象と拡散現象のおさらい
移流方程式(1次元と2次元)
移流(Advection)とは、流体中に存在する物質や物理量(温度等)の分布がそのままの形で移動する現象を指します。気体や液体は固体よりも自由に形を変えるため、物理量自体も流される特性を持ちます。
当ブログは以下の記事で1次元移流方程式の数値計算を行いました。移流現象をコンピュータで安定計算するためには離散化に工夫が必要でした。
Pythonで1次元移流方程式を離散化して数値流体力学に入門する
参考までに、1次元移流方程式の数値解析結果例を以下に示します。
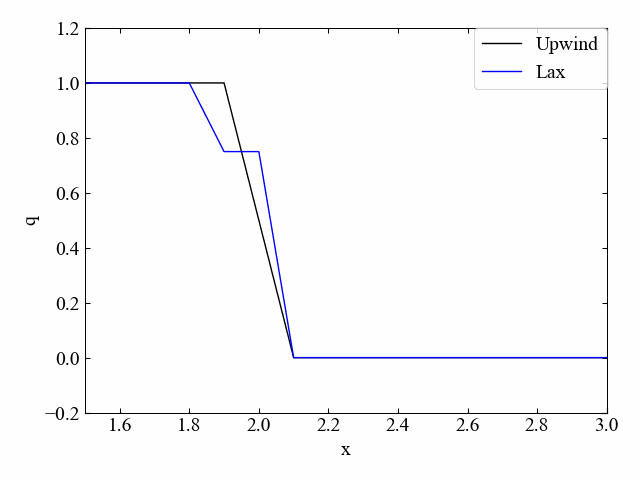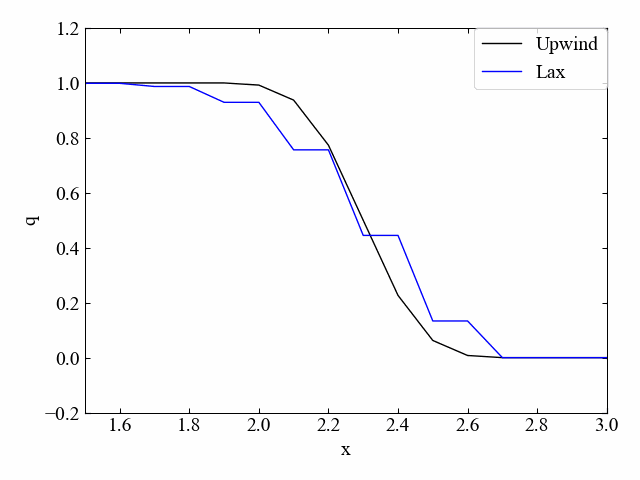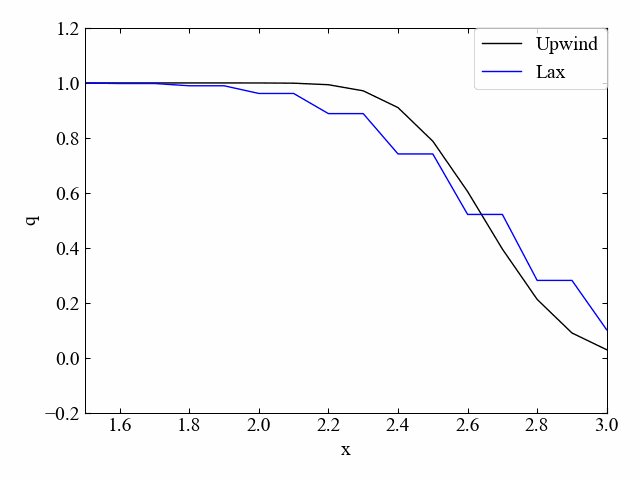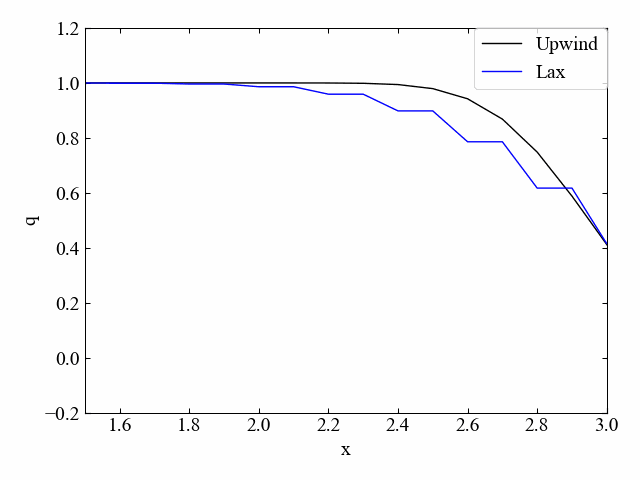
また以下の記事で2次元移流方程式の数値計算を行いました。2次元になったとしても基本的に離散化手法に特別なことはありません。ただし、2次元におけるプログラミングは少し1次元と異なる点が多いので、2次元流体シミュレーションの例題として是非記事をご覧ください。
2次元移流方程式の数値解析結果例を以下に示します。拡散しているように見えますが、これは拡散現象を方程式に入れたのではなく、数値拡散効果です。
拡散方程式(1次元と2次元)
拡散(Diffusion)とは、液体や気体、温度といった熱流体が散らばっていき、化学変化を伴わずに次第に全体が均一になっていく現象のことです。
移流と同様に、当ブログでは拡散方程式についても数値計算を行いました。以下の2つの記事で1次元と2次元の拡散方程式を扱っていますので是非記事を読んでみてください。
Pythonで拡散方程式を数値計算してアニメーションを作成する
Pythonで2次元拡散方程式を数値解析して定常解析と比較する
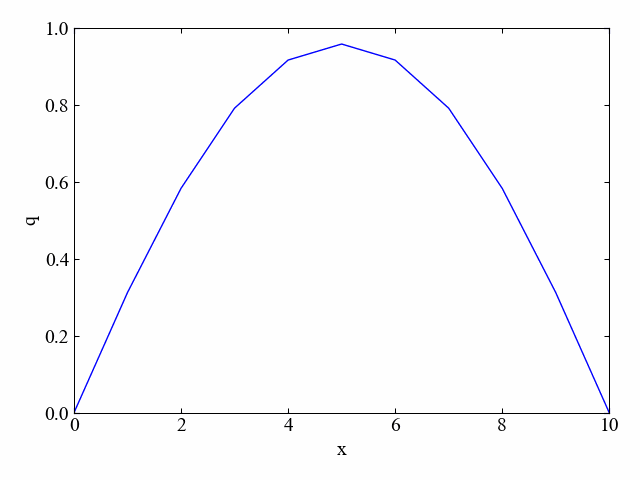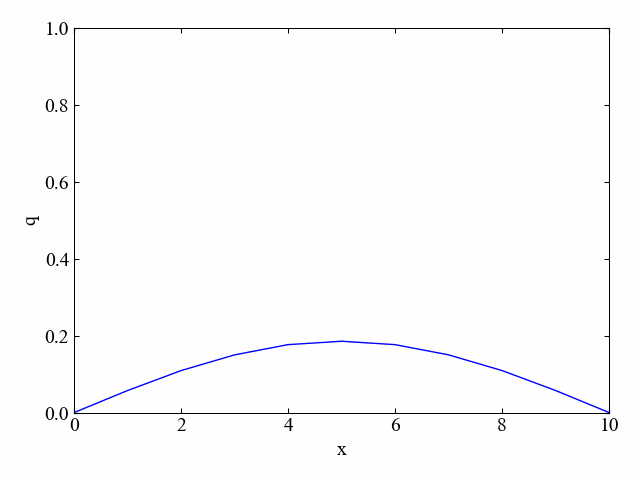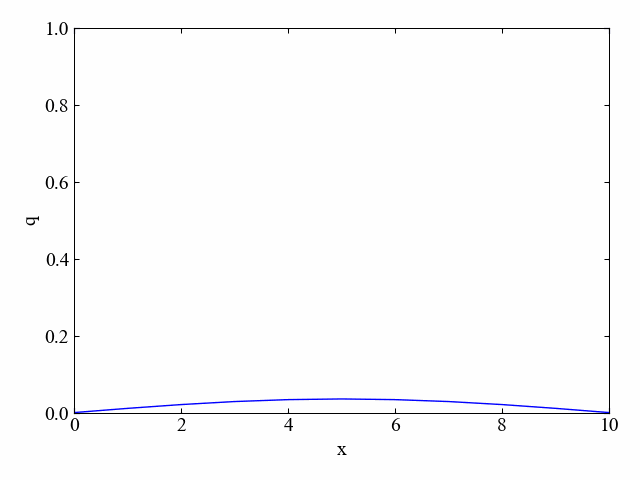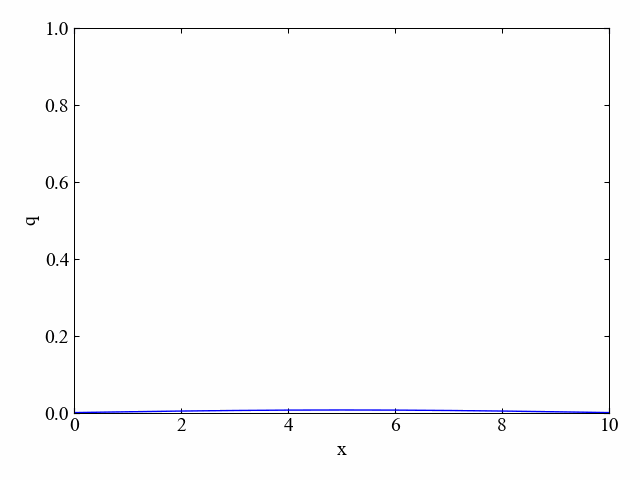
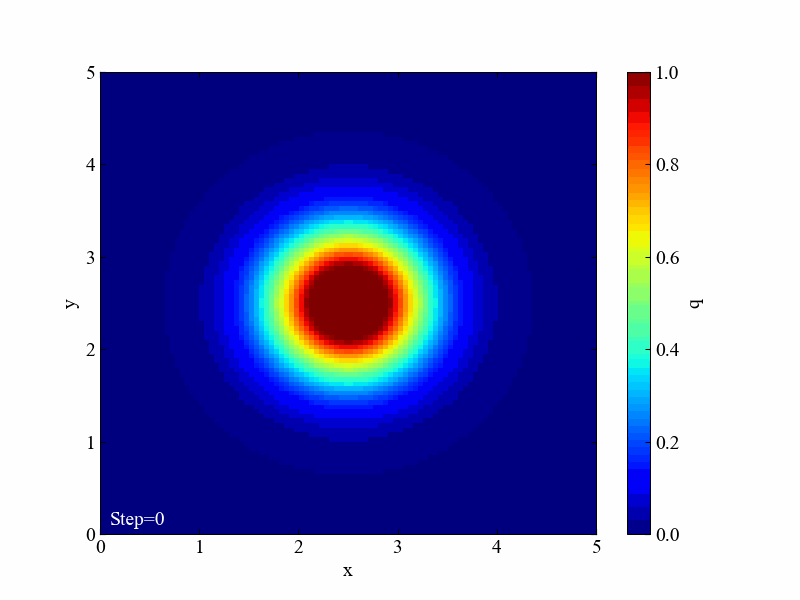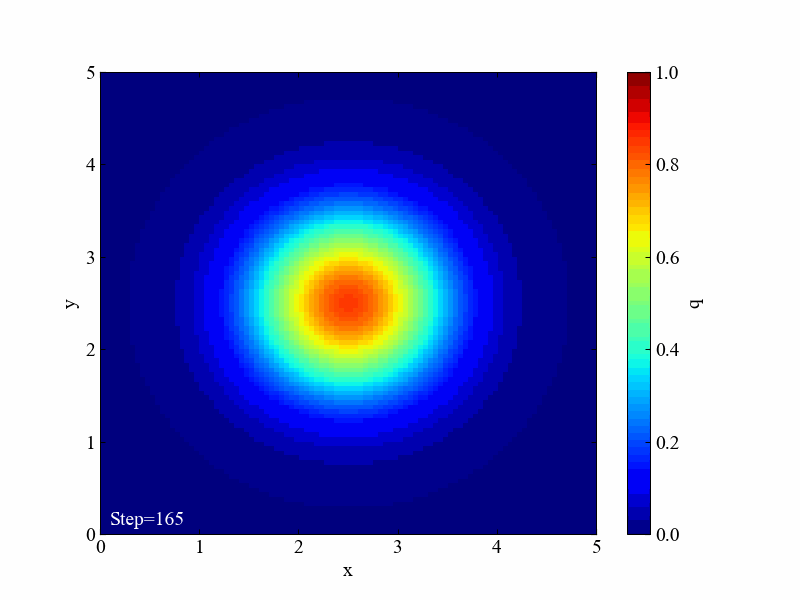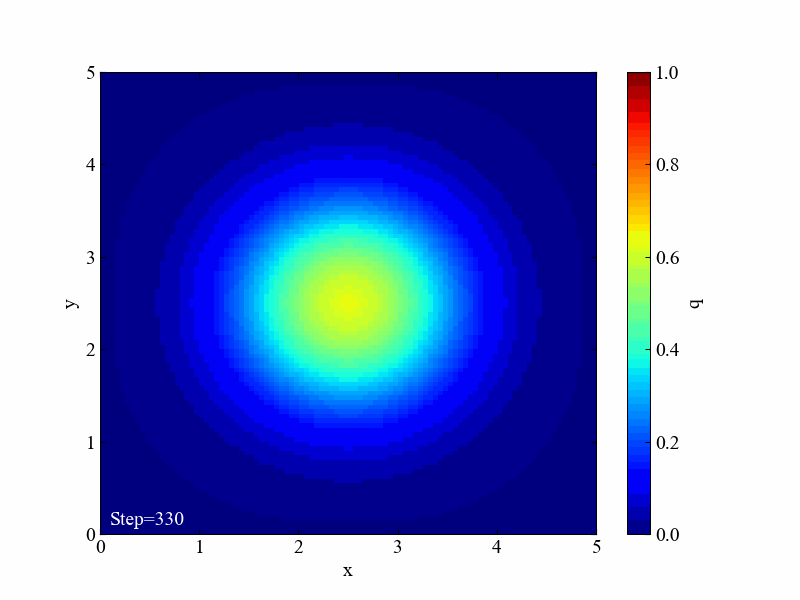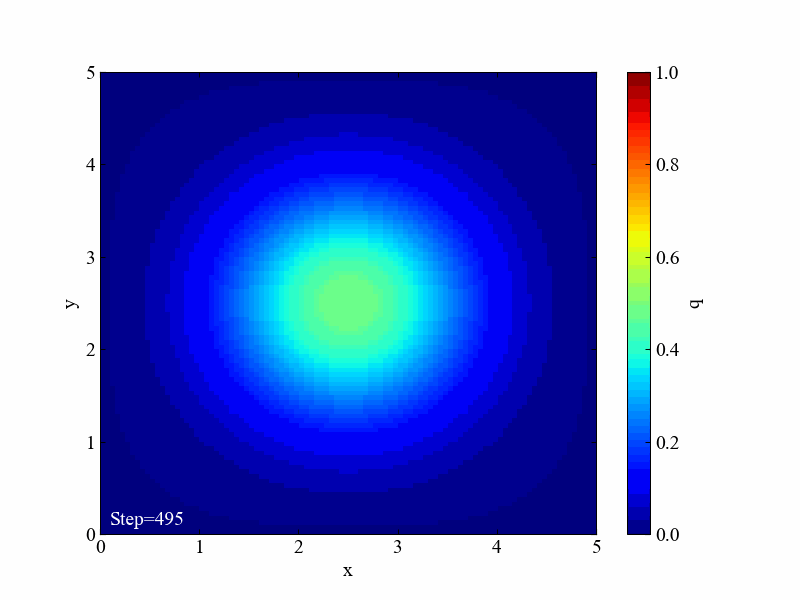
このように拡散方程式は場を均一にさせようとする効果があります。
2次元移流拡散方程式を数値計算するPythonコード例
これまでと同様に最後にコピペ動作用の全コードを紹介しますが、主要な設定を1つずつコード付きで解説します。
動作環境
このページでは以下の環境で動作確認を行ったコードを掲載しています。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
| pillow | 7.1.2 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
格子生成と初期場
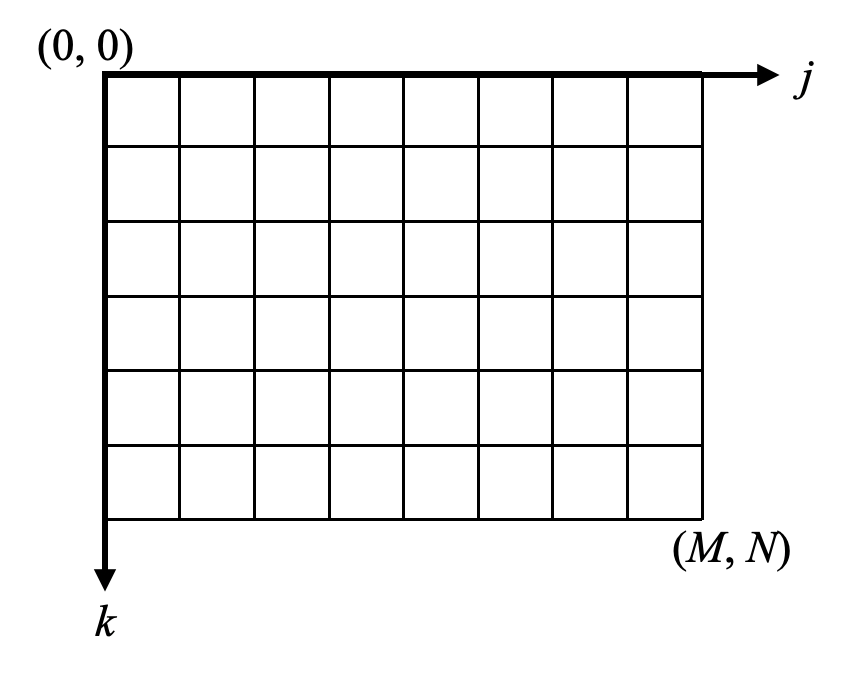
格子はいつも通りj, kの格子番号で表現できる直交格子を用います。
そして初期場はinitial_field関数で設定します。今回の例では初期場として全ての数値を0で埋めます。
コードはこちら。
|
1 2 3 4 5 6 7 8 9 |
def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場(x方向をj, y方向をkとする行列を作成→2D画像のデータ構造を模擬) x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(y), len(x))) return x, y, z |
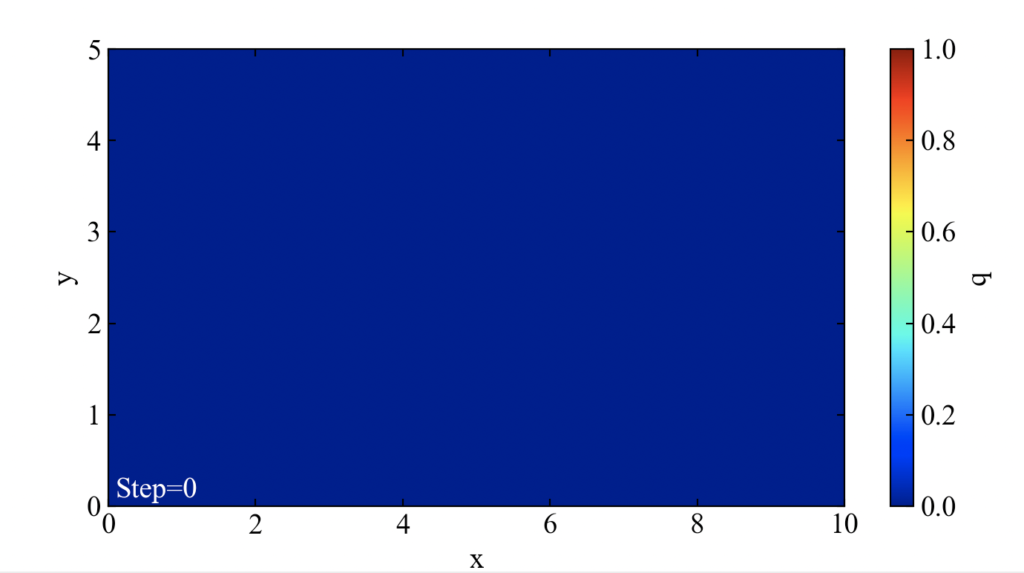
このコードで得られる初期場を下図に示します。
速度条件と拡散係数
移流拡散方程式の移流項に付与する速度と拡散項に付与する拡散係数を以下のように設定します。ここではx方向(j方向)に一様な流れ、拡散係数には等方的に1を与えます。
|
1 2 3 4 5 6 |
# 輸送速度c, d c = 1 d = 0 # 拡散係数k k = 1 |
境界条件
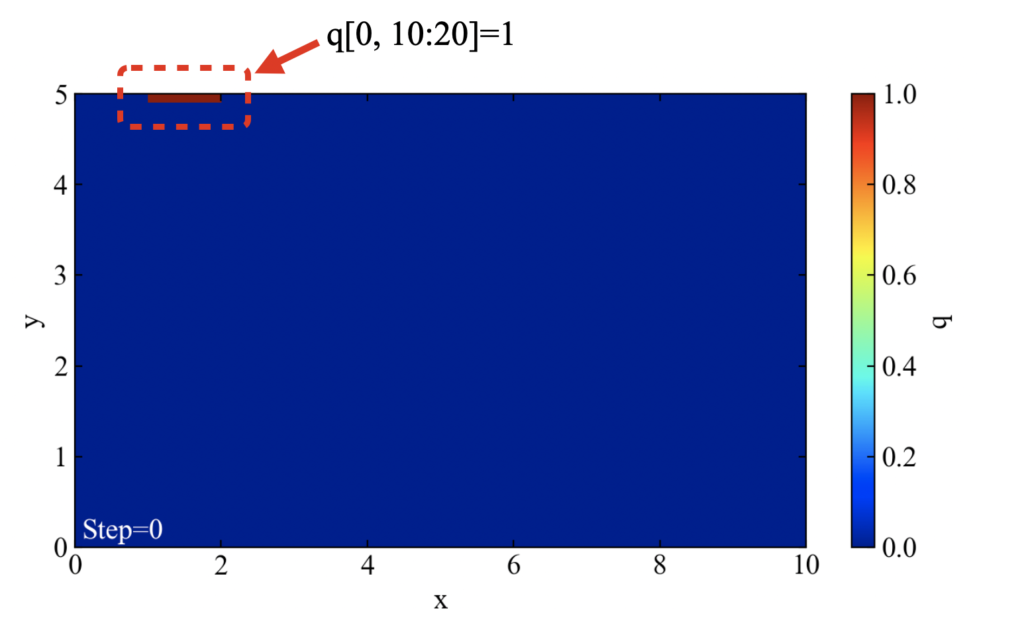
境界条件は移流現象と拡散現象をよく確認できるよう、上辺に一区間のみ1を、それ以外の辺には0というディリクレ条件を与えます。
これはある流れ場に上辺からインクを垂らし続けたような状況を想定しました。
|
1 2 3 4 5 6 7 8 9 10 |
def boundary_condition(z): ''' 分布に境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, 10:20] = 1 z[-1, :] = 0 return z |
ソルバー(基礎方程式と離散化)
移流拡散方程式の基礎方程式を式(1)に示します。この方程式は左辺第1項が時間項、左辺第2項が移流項、そして右辺が拡散項です。
2次元空間における方程式は式(1)のナブラ\(\nabla\)を展開して式(2)と表現します。この式(2)が2次元の移流拡散方程式です。
そして式(3)が離散式です。過去の記事の離散化手法をそのまま使っていますので、詳細な式展開は先ほど紹介した記事をご確認ください。
ソルバー部分はsol_2d_advection_diffusion関数で行います。やたらとfor文を書いているところはNumPyをうまく使えば改善可能と思います…が今回はこのまま。
実行すると初期場のプロット、境界条件のプロットが表示されます。×マークで閉じたら計算ループが開始されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
def sol_2d_advection_diffusion(x, y, q, dt, dx, dy, c, d, k, step, dir, result_interval): ''' 輸送速度が正の2次元移流拡散方程式を数値計算する ''' # 漸化式を反復計算 q = q.T for i in range(step): q0 = q.copy() for j in range(1, len(q) - 1): for k in range(1, len(q.T) - 1): a = c * (dt / dx) b = d * (dt / dy) r = a * (dt / dx ** 2) s = a * (dt / dy ** 2) q[j, k] = q0[j, k] - a * (q0[j, k] - q0[j-1, k]) - b * (q0[j, k] - q0[j, k-1]) \ + r * (q0[j+1, k] - 2 * q0[j, k] + q0[j-1, k]) \ + s * (q0[j, k+1] - 2 * q0[j, k] + q0[j, k-1]) # 境界条件を設定 q = q.T q = boundary_condition(q) q = q.T # 指定した間隔で画像保存 if i % result_interval == 0: print('Iteration=', i) q = q.T plot(x, y, q, i, dir, 1) q = q.T return |
全コード
コピペ動作する全コードを以下に紹介します。是非初期場や境界条件を変えてシミュレーションしてみてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 |
import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場(x方向をj, y方向をkとする行列を作成→2D画像のデータ構造を模擬) x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(y), len(x))) return x, y, z def boundary_condition(z): ''' 分布に境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, 10:20] = 1 z[-1, :] = 0 return z def sol_2d_advection_diffusion(x, y, q, dt, dx, dy, c, d, k, step, dir, result_interval): ''' 輸送速度が正の2次元移流拡散方程式を数値計算する ''' # 漸化式を反復計算 q = q.T for i in range(step): q0 = q.copy() for j in range(1, len(q) - 1): for n in range(1, len(q.T) - 1): a = c * (dt / dx) b = d * (dt / dy) r = k * (dt / dx ** 2) s = k * (dt / dy ** 2) q[j, n] = q0[j, n] - a * (q0[j, n] - q0[j - 1, n]) - b * (q0[j, n] - q0[j, n - 1]) \ + r * (q0[j + 1, n] - 2 * q0[j, n] + q0[j - 1, n]) \ + s * (q0[j, n + 1] - 2 * q0[j, n] + q0[j, n - 1]) # 境界条件を設定 q = q.T q = boundary_condition(q) q = q.T # 指定した間隔で画像保存 if i % result_interval == 0: print('Iteration=', i) q = q.T plot(x, y, q, i, dir, 1) q = q.T return def plot(x, y, z, i, dir, save_flag): ''' 関数をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意して上下左右に目盛線を付ける。 x_size = 8 y_size = int(1 * x_size * (np.max(y) / np.max(x))) fig = plt.figure(figsize=(x_size, y_size)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 im = ax1.imshow(z, vmin=0, vmax=1, extent=[np.min(x), np.max(x), np.min(y), np.max(y)], aspect='auto', cmap='jet') ax1.text(0.1, 0.1, 'Step='+str(i), color="white") # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('q') # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) if save_flag == 1: # 画像を保存する plt.savefig(path) else: # グラフを表示する。 plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) imgs = [] # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=50, loop=0) return if __name__ == '__main__': ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する ''' # 画像保存フォルダと動画ファイル名 dir = 'img_2d_advection-diffusion' filename = '2d-advection-diffusion.gif' # 時間項の条件 dt = 0.01 # 空間項の条件 dx = 0.1 dy = 0.1 x_max = 10 y_max = 5 # 初期場を用意する x, y, q = initial_field(x_max, y_max, dx, dy) plot(x, y, q, 0, dir, 0) # 輸送速度c, d c = 1 d = 0 # 拡散係数k k = 0.1 # 移流項の安定性確認 advection_x = c * dt / dx advection_y = d * dt / dy print('Advection:x, y=', advection_x, advection_y) # 安定性の確認 diffusion_x = k * dt / dx ** 2 diffusion_y = k * dt / dy ** 2 print('Diffusion:x, y=', diffusion_x, diffusion_y) # 境界条件を設定 q = boundary_condition(q) plot(x, y, q, 0, dir, 0) # 計算を実行 sol_2d_advection_diffusion(x, y, q, dt, dx, dy, c, d, k, 500, dir, 5) # GIF動画を作成 create_gif(dir, filename) |
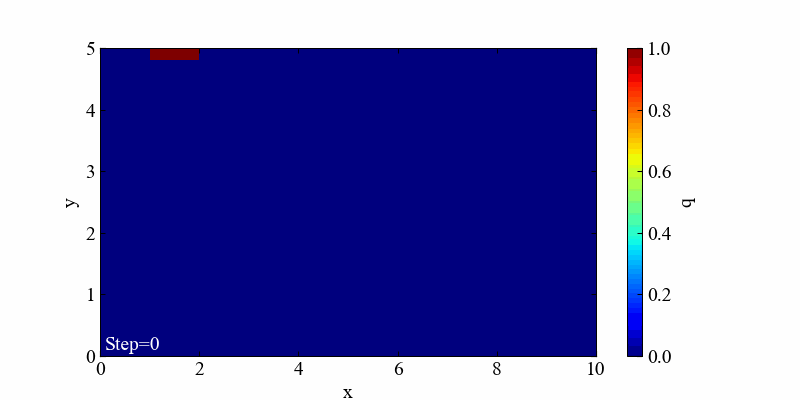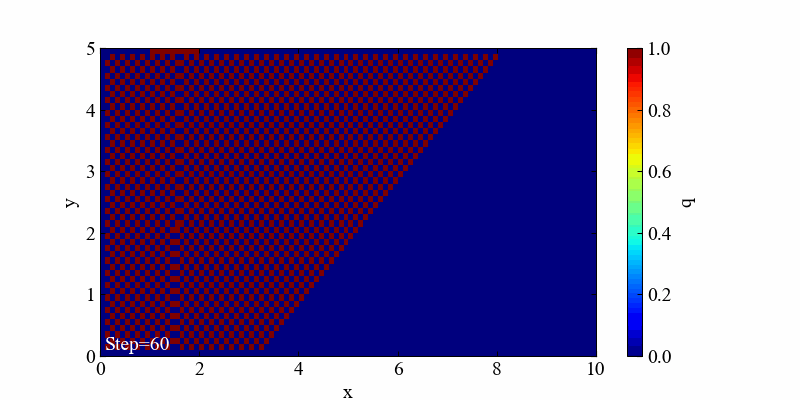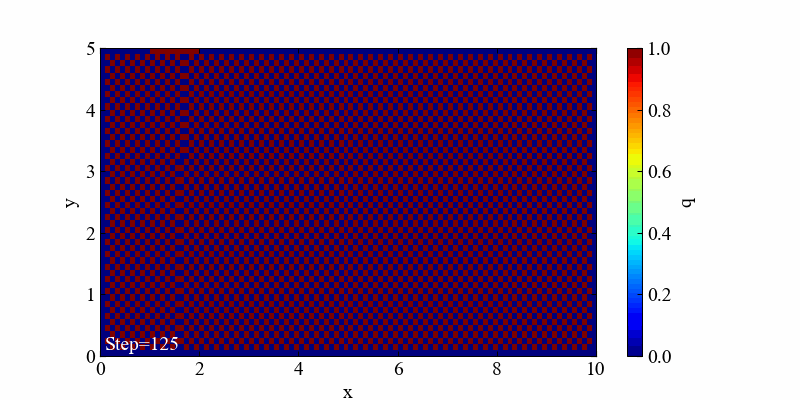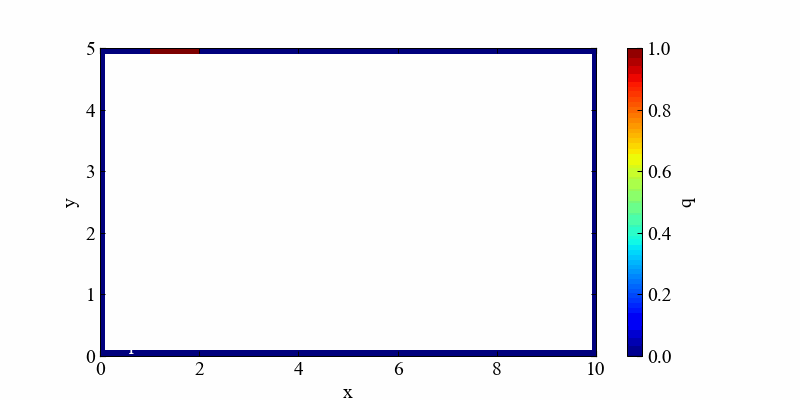
実行結果
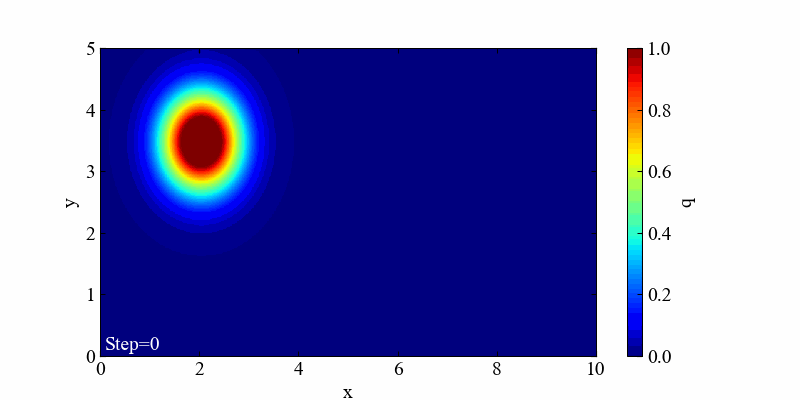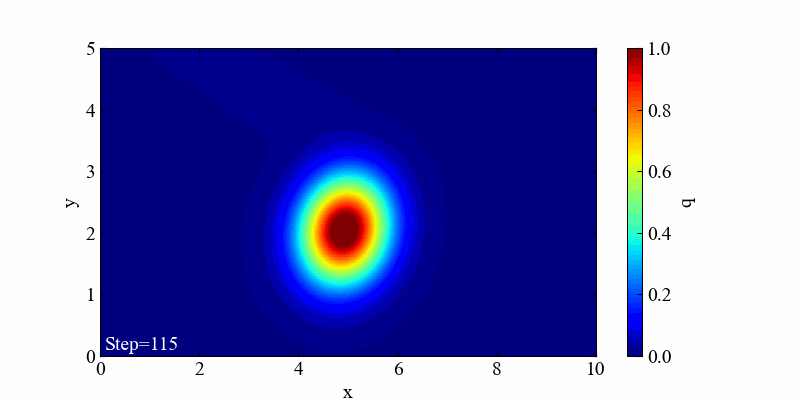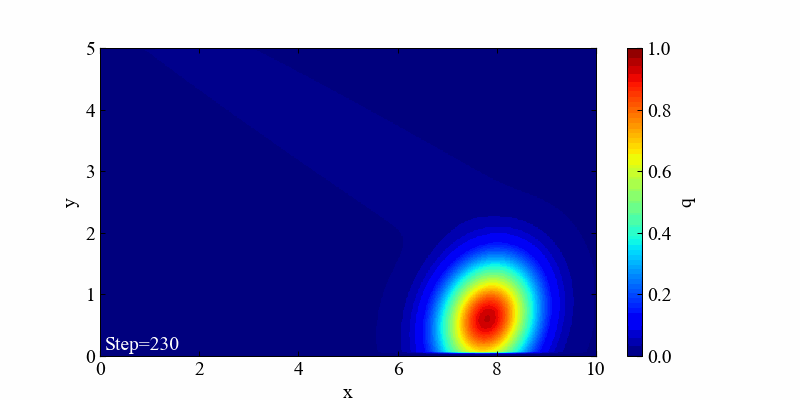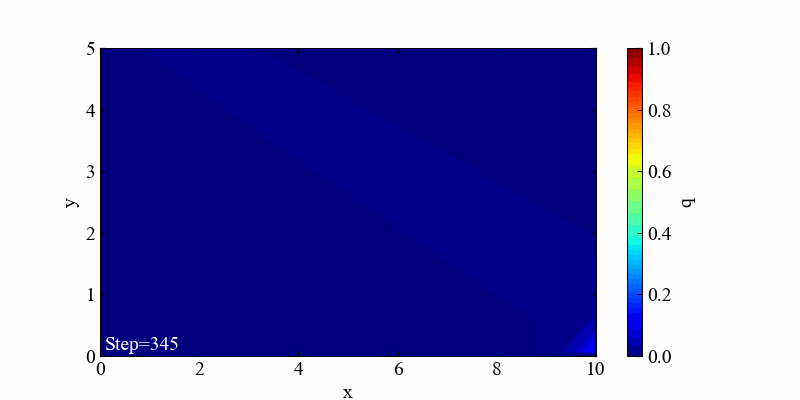
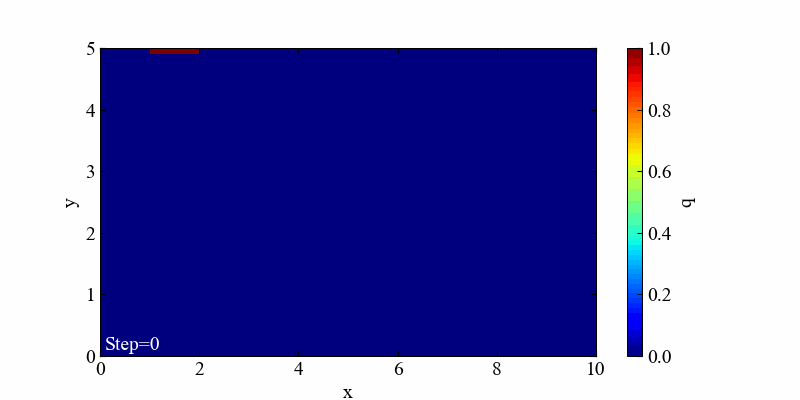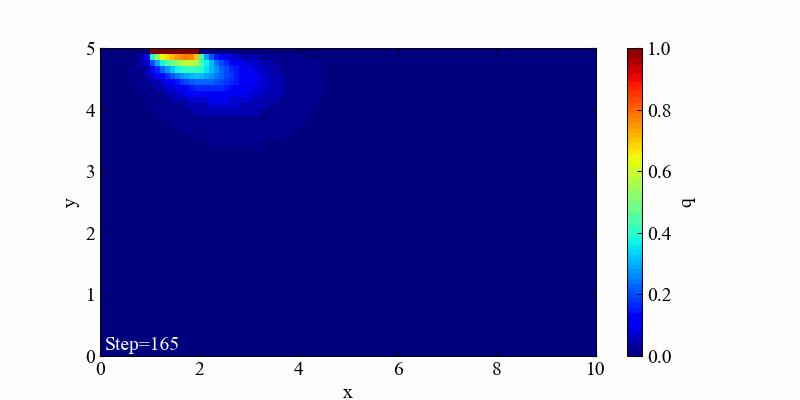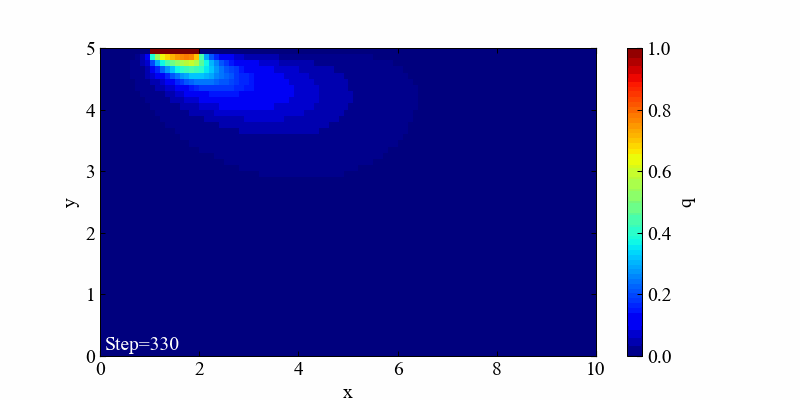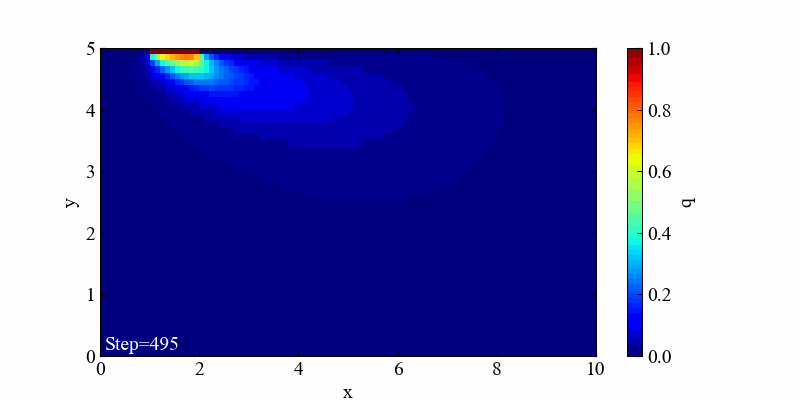
この境界条件における結果は「移流」と「拡散」の両方の特徴を良く表現した流れとなっていると思います。
実行結果(発散例)
最後はオチとしていつも通りの発散動画を紹介します。以下の結果はdt=1.0と大きくした場合。「RuntimeWarning: overflow encountered in double_scalars」というエラーが出るほどの結果となりました。ちょっとやりすぎました。
まとめ
本記事ではこれまで学んだ「移流」と「拡散」現象を組み合わせた「移流拡散方程式」を学びました。
基礎方程式と離散化式を紹介し、Pythonでコーディングを行いましたが、内容はこれまで学んだことの組み合わせというものでした。
移流拡散の両方の現象を含んだ例題として、格子の一部境界にディリクレ条件を付加する条件で数値計算を行いました。
流れの中に落としたインクが広がりながら移動するような結果が得られ、目的の流れを再現するコーディングができたと思います。
境界条件はもう少し真面目に考えないといけないかも知れませんし、まだまだ詳細な流体現象を記述したナビエ・ストークス方程式を数値計算したわけではありません。しかし回を重ねる毎にだんだんと流れのシミュレーションっぽくなってきた感じがします。
移動しながら拡散する現象までシミュレートすることができました!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
はじめまして。一連の解説+スクリプトを参考にさせて頂いています。ありがとうございます。
勘違いでしたら申し訳ないですが、今回のコードのsol_2d_advection_diffusionの中で、r
とsが
r = a * (dt / dx ** 2)
s = a * (dt / dy ** 2)
となっていますが、解説の基礎方程式を参照すると、これはaではなく、拡散係数のk を掛けるのが正しくないでしょうか?
また、for loop にk を使われているため、肝心の拡散係数が使われていない形になっていないでしょうか?
私の勘違いでしたら恐縮ですが、ご確認よろしくお願いします
ご訪問ありがとうございます。
コードを見直したところ、関数の引数kが参照されていない、かつkが使われていないことをこちらも確認しました。
ご指摘ありがとうございました。