2019.06.10

Pythonで1自由度減衰系の自由振動シミュレーション

前回はばねと質点のみのモデルを扱いましたが、今回は減衰を考慮したモデルのシミュレーションをPythonで学びます。

こんにちは。wat(@watlablog)です。
単一の質点をベースとした系からは様々な本質的なことが学べます。今回はばね質点系にダンパーという減衰を追加したモデルのシミュレーションをPythonで学びます。

目次（項目クリックでジャンプできます）

1自由度減衰系とは？

前回の記事「Pythonで1自由度非減衰系の自由振動シミュレーション」では非減衰系を扱いましたが、今回は減衰系を扱います。

以下の図が1自由度減衰系のモデルです。1つの質点にばねとダンパー（ダッシュポットとも言う）が並列に接続されたモデルです。

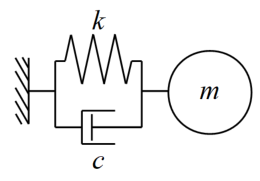
このダンパーというのは、現実の構造物には必ず含まれている要素で、減衰効果を発生させます。

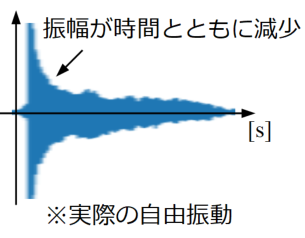
実際の自由振動の例を以下の図に示します。

この図はピアノのA音を打鍵した時の音圧信号を示していますが、時間とともに振幅がどんどん小さくなっています。打鍵したら永遠に音が鳴り続けるピアノがあり得ないことは、誰しも感覚的によくわかることと思いますが、振動現象としてしっかり説明するためには減衰の理解が必要です。

以下の式が今回対象とする1自由度減衰系の自由振動を説明するための運動方程式です。

$$m\ddot{x}+c\dot{x}+kx= 0 (1)$$

前回の非減衰系と比べると、減衰係数$c$[N・s/m]が入っているのが違いとなります。今回はこの方程式をPythonでシミュレーションしてみます！

Pythonによる振動シミュレーションのコード

全コード

コードの内容は前回の記事である「Pythonで1自由度非減衰系の自由振動シミュレーション」とほとんど同じです。

ここでは変化点のみを記載します。

まず変数変換を式(2)で行う所は一緒です。

\[ \begin{cases}
x_{1}= x \\
x_{2}= \dot{x}
\end{cases}　(2)
\]

これを$\dot{x_{2}}$について整理することで以下の式(3)を得ます。

$$\dot{x_{2}}= -\frac{c}{m}x_{2}-\frac{k}{m}x_{1}　(3)$$

今回のシミュレーションの全コードを以下に示します。

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# mk system
def func(state,t, m, k, c):
    x1, x2 = state
    dx2dt = - (c/m) * x2 - (k/m) * x1
    return [x2, dx2dt]

m = 0.5                         # 質量[kg]
k = 1000                        # 剛性[N/m]
c = 5
state0 = [0.1, 0.0]             # 初期値[x0, v0]

t0 = 0                          # 初期時間[s]
tf = 1                          # 終了時間[s]
dt = 0.005                      # 時間刻み[s]
t = np.arange(t0, tf+dt, dt)    # 時間軸配列

# odeintを使った解法
# x1, x2の解を求めているので、sol[0]が変位x1, sol[1]が速度x2となる
sol = odeint(func, state0, t, args=(m, k, c))

# ここから理論値計算
cc = 2 * np.sqrt(m * k)
zeta = c / cc
omega = np.sqrt(k / m)
omega_d = omega * np.sqrt(1 - np.power(zeta, 2))
sigma = omega_d * zeta
X = np.sqrt(np.power(state0[0], 2) + np.power((state0[1] + sigma * state0[0])/omega_d, 2))
phi = np.arctan((state0[1] + (sigma * state0[0]))/(state0[0] * omega_d))

theory = np.exp(- sigma * t) * X * np.cos(omega_d * t - phi)
# ここまで理論値計算

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Displacement [m]')

# データプロット
ax1.plot(t, sol[:,0], label='Python odeint [x0=0.1, v0=0.0]', c='b', marker='o', linestyle='None')
ax1.plot(t, theory, label='Theory', c='r')

fig.tight_layout()
plt.legend(loc='upper right')

# グラフを表示する。
plt.show()
plt.close()

import numpy as np

from scipy.integrate import odeint

import matplotlib.pyplot as plt

# mk system

def func(state,t, m, k, c):

x1, x2 = state

dx2dt = - (c/m) * x2 - (k/m) * x1

return [x2, dx2dt]

m = 0.5 # 質量[kg]

k = 1000 # 剛性[N/m]

c = 5

state0 = [0.1, 0.0] # 初期値[x0, v0]

t0 = 0 # 初期時間[s]

tf = 1 # 終了時間[s]

dt = 0.005 # 時間刻み[s]

t = np.arange(t0, tf+dt, dt) # 時間軸配列

# odeintを使った解法

# x1, x2の解を求めているので、sol[0]が変位x1, sol[1]が速度x2となる

sol = odeint(func, state0, t, args=(m, k, c))

# ここから理論値計算

cc = 2 * np.sqrt(m * k)

zeta = c / cc

omega = np.sqrt(k / m)

omega_d = omega * np.sqrt(1 - np.power(zeta, 2))

sigma = omega_d * zeta

X = np.sqrt(np.power(state0[0], 2) + np.power((state0[1] + sigma * state0[0])/omega_d, 2))

phi = np.arctan((state0[1] + (sigma * state0[0]))/(state0[0] * omega_d))

theory = np.exp(- sigma * t) * X * np.cos(omega_d * t - phi)

# ここまで理論値計算

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('Displacement [m]')

# データプロット

ax1.plot(t, sol[:,0], label='Python odeint [x0=0.1, v0=0.0]', c='b', marker='o', linestyle='None')

ax1.plot(t, theory, label='Theory', c='r')

fig.tight_layout()

plt.legend(loc='upper right')

# グラフを表示する。

plt.show()

plt.close()

理論値の計算（減衰振動($0<\zeta<1$)の場合）

先ほどの全コードには既に理論値の式が入っていますが、ここではシミュレーションと比較するための理論値の計算を説明します。

減衰を含む系では臨界減衰係数$c_{c}$という重要なパラメータが存在します。この臨界減衰係数は質量$m$と剛性$k$によって式(4)により一意に決まります。

$$c_{c}= 2\sqrt{mk}　(4)$$

臨界減衰係数$c_{c}$は式(5)の減衰比$\zeta$を計算する時に使います。後で説明しますが、この減衰比$\zeta$は系の振動の仕方を判断する重要な因子です。

$$\zeta= \frac{c}{c_{c}}　(5)$$

固有角振動数$\omega$は前回の非減衰系では式(6)で決まりましたが、減衰を含む自由振動の固有振動数は式(7)になります。

$$\omega= \sqrt{{\frac{k}{m}}}　(6)$$

$$\omega _{d}= \omega \sqrt{1-\zeta ^{2}}　(7)$$

理論値は式の見た目を簡単にするために式(8)と式(9)、そして式(10)を導入して式(11)を使って算出します。

$$\sigma = \omega \zeta　(8) $$

$$X= \sqrt{x_{0}^{2}+\left ( \frac{v_{0}+\sigma x_{0}}{\omega _{d}} \right )^{2}}　(9)$$

$$\phi = tan^{-1}\left ( \frac{v_{0}+\sigma x_{0}}{x_{0}\omega _{d}} \right )　(10)$$

$$x= e^{-\sigma t}Xcos\left ( \omega _{d}t-\phi \right )　(11)$$

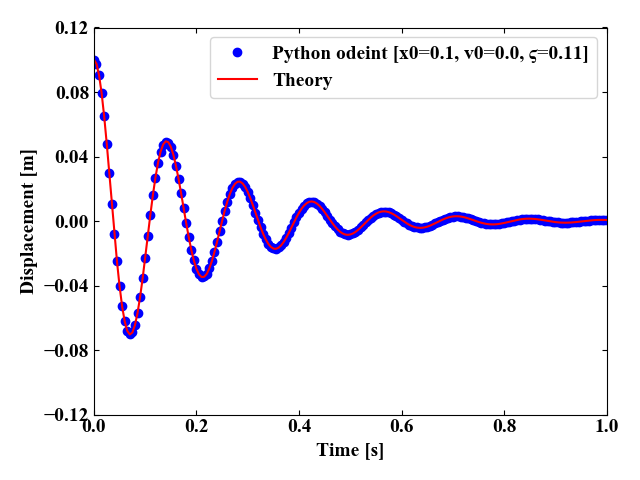
実行結果（理論値との比較）

以下が今回のPythonプログラムの実行結果です。$\zeta=0.11$の場合、初めは振動していた質点も次第に減衰し止まっていく様子がわかります。

odeintによる数値計算結果は理論値ともよく一致していることがわかります。

実行結果（$\zeta$の違いによる振る舞いを観察）

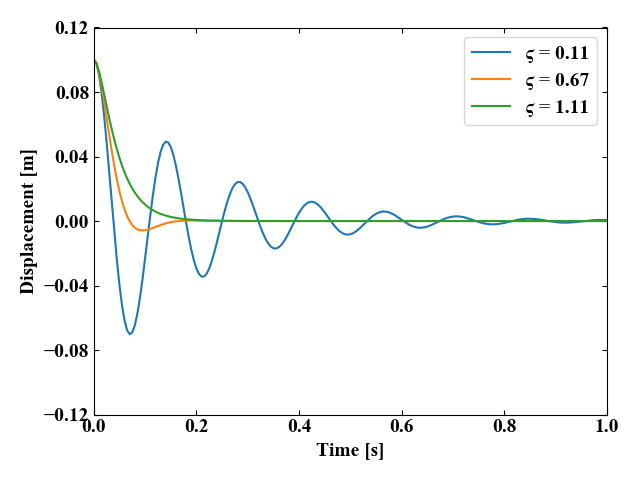
以下の図は減衰比$\zeta$を3パターンに振って振動の振る舞いを観察してみた結果です。

減衰比$\zeta$が1より小さい場合は振動はしますが、時間により振幅が減衰する減衰振動の状態になります。

一方、$\zeta$が1を超えると、振動現象は一切起こらない過減衰の状態になります。

ちなみに$\zeta=1$の場合を臨界減衰と呼びます。

追記：理論値の場合分け

$\zeta$による式の変化

上の理論式は減衰振動にのみ対応していました。汎用性が無いので、減衰比による場合分けに対応させてみます。

しかし…式の導出は少々長いので、Wikipediaの減衰振動のページをカンニングしました！

まず、無次元初期速度を式(12)とおくと、

\[
\sigma_{v0} = \frac{v_{0}}{x_{0} \omega} \tag{12}
\]

$\zeta = 1$ の臨界減衰の場合の変位$x$は式(13)となります。

\[ x=x_{0}e^{- \omega t} \left \{ (\sigma_{v0} + 1) \omega t + 1 \right \}\tag{13} \]

また、$\zeta>1$の過減衰の場合の変位$x$は式(14)になります。

\[ x=x_{0}e^{-\zeta \omega t}\left \{\cosh \left ( \omega t \sqrt{\zeta^{2}-1}\right ) + \frac{\sigma_{v0}+\zeta}{\sqrt{\zeta^{2}-1}}\sinh \left ( \omega t \sqrt{\zeta^2-1}\right ) \right \}\tag{14} \]

Pythonコード

上のPythonコードで、理論値計算部分を以下に置き換えることで、理論値の条件分岐を表現します。

# ここから理論値計算---------------------------------------------------------------------------
cc = 2 * np.sqrt(m * k)
zeta = c / cc
omega = np.sqrt(k / m)
omega_d = omega * np.sqrt(1 - np.power(zeta, 2))
sigma = omega_d * zeta

n_order_v = state0[1] / (state0[0] * omega)

# 減衰振動の場合
if zeta < 1:
    X = np.sqrt(np.power(state0[0], 2) + np.power((state0[1] + sigma * state0[0])/omega_d, 2))
    phi = np.arctan((state0[1] + (sigma * state0[0]))/(state0[0] * omega_d))
    theory = np.exp(- sigma * t) * X * np.cos(omega_d * t - phi)
# 臨界減衰の場合
elif zeta == 1:
    theory = state0[0] * np.exp(- omega * t) * ((n_order_v + 1) * omega * t + 1)
# 過減衰の場合
else:
    theory = state0[0] * np.exp(- zeta * omega * t) * (\
        np.cosh(omega * t * np.sqrt(zeta ** 2 - 1))\
        + (n_order_v + zeta) / (np.sqrt(zeta ** 2 + 1))\
        * np.sinh(omega * t * np.sqrt(zeta ** 2 - 1)))
# ここまで理論値計算---------------------------------------------------------------------------

# ここから理論値計算---------------------------------------------------------------------------

cc = 2 * np.sqrt(m * k)

zeta = c / cc

omega = np.sqrt(k / m)

omega_d = omega * np.sqrt(1 - np.power(zeta, 2))

sigma = omega_d * zeta

n_order_v = state0[1] / (state0[0] * omega)

# 減衰振動の場合

if zeta < 1:

X = np.sqrt(np.power(state0[0], 2) + np.power((state0[1] + sigma * state0[0])/omega_d, 2))

phi = np.arctan((state0[1] + (sigma * state0[0]))/(state0[0] * omega_d))

theory = np.exp(- sigma * t) * X * np.cos(omega_d * t - phi)

# 臨界減衰の場合

elif zeta == 1:

theory = state0[0] * np.exp(- omega * t) * ((n_order_v + 1) * omega * t + 1)

# 過減衰の場合

else:

theory = state0[0] * np.exp(- zeta * omega * t) * (\

np.cosh(omega * t * np.sqrt(zeta ** 2 - 1))\

+ (n_order_v + zeta) / (np.sqrt(zeta ** 2 + 1))\

* np.sinh(omega * t * np.sqrt(zeta ** 2 - 1)))

# ここまで理論値計算---------------------------------------------------------------------------

$\zeta$による理論値と解析値の比較

まずは減衰振動（$0 < \zeta < 1$）の場合です。コード内でわかりやすく減衰係数の値を「c = 2 * np.sqrt(m * k) * 0.1」と$\zeta=0.1$となるようにして実行すると、以下の図を得ます。

続いて臨界減衰振動（$\zeta=1$）となるように、「c = 2 * np.sqrt(m * k) * 1.0」と変更して実行すると以下の図を得ます。

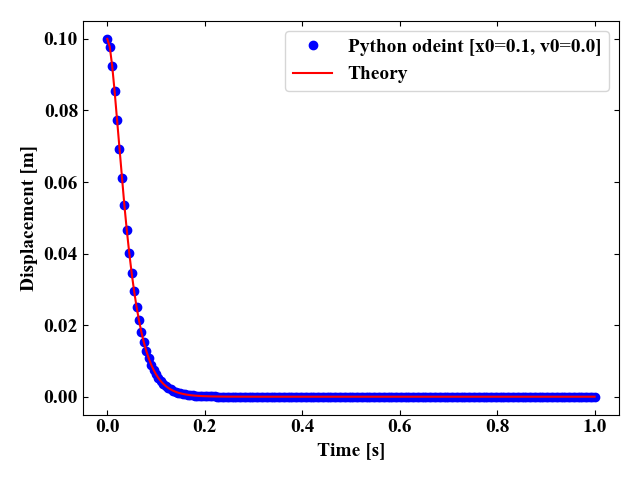
最後に、過減衰($\zeta>1$)となるよう「c = 2 * np.sqrt(m * k) * 2.0」と変更して実行すると以下の図を得ます。

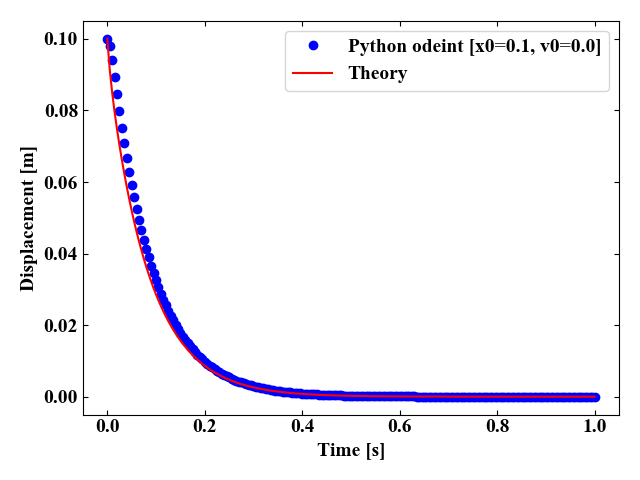
概ね近しい結果を得ました。
ただ、$\zeta=0.9$や$\zeta=1.1$付近になると理論値と解析値の乖離が大きくなるようです。

（コード内の式のトレースを間違っている可能性もありますが…、解析誤差？ここらへんはまだ検証をしていません）

まとめ

本ページでは1自由度の減衰系の運動方程式を紹介し、Pythonによるシミュレーションのコーディングを紹介しました。

基本は前回の非減衰系と同じで、odeintによる数値計算結果は、理論値と比較しても問題無いレベルであると確認しました。

これで1自由度非減衰と減衰系の振動シミュレーションができるようになりました！振動は強制振動、多自由度とこの後進みますが、全ての基本はここにあります！

Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

wat

機械工学を専攻し大学院を修了後、技術系の職に就き日々実験やシミュレーションを使う仕事をしています。このブログでは初心者が科学技術プログラムを作れるようになることを目標に、学習結果を記録していきます。著書「いきなりプログラミングPython（翔泳社）」 ※資格・計算力学技術者 1級 2級 (振動) ・計算力学技術者 2級 (熱流体) ・基本情報技術者・G検定・AI実装検定 S級 A級 ※Information ・Amazonのアソシエイトとして、当メディアは適格販売により収入を得ています。・当メディアはGoogleによるユーザーに合わせた自動広告が表示されます。

鈴木　高登より:

2020年5月26日 4:41 PM

はじめまして、ただいま大学院生ものです。
Pythonを使って、1自由度減衰系の解析プログラミングを構築したいと思っていますが、なかなか実行できません。
内容としては、減衰比の場合分けに関してのグラフを作りたいです。
コードを教えていただけたら幸いです。よろしくお願い致します。

返信
1. wat より:
  
  2020年5月26日 10:16 PM
  
  コメントありがとうございます！
  Pythonのodeintは減衰比の値によって場合分けする必要もなく解析をしてくれます。
  ここで言う「減衰比の場合分け」とは、本ページに載せている「理論値」が過減衰や臨界減衰に対応していないため、それらに対応させて解析と理論を比較したいということでしょうか？
  そういう事であれば、本ページの「追記：理論値の場合分け」を追記しましたのでご覧頂きたいと思います（違ったらすみません…！）。
  
  返信
Masa より:

2022年12月14日 1:57 AM

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def func(state,t,m,k,c):
x1,x2 = state
dx2dt = -(c/m) * x2 -(k/m) * x1
return[x2,dx2dt]
m = 0.5
k = 800
c = 4
state0 = [0.0,0.0]
t0 = 0
tf = 0.5
dt = 0.05
t = np.arange(t0, tf+dt, dt)
plt.rcParams[‘font.size’] = 12
plt.rcParams[‘font.family’] = ‘DejaVu Serif’
plt.rcParams[‘xtick.direction’] = ‘in’
plt.rcParams[‘ytick.direction’] = ‘in’
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position(‘both’)
ax1.xaxis.set_ticks_position(‘both’)
ax1.set_xlabel(‘Time [s]’)
ax1.set_ylabel(‘Displacement [m]’)
plt.title(‘graph’)
ax1.plot(t, sol[:,0], label=’Python odeint [x0=1.0, v0=0.0]’, c=’b’, marker=’o’, linestyle=’None’)

fig.tight_layout()
plt.legend(loc=’upper right’)
plt.show()
plt.close()

このようにwatさんのをまねて理論値の部分は除いてプログラミングを作ってみたのですが、実際に実行するとグラフの外枠や目盛りは書かれるのですが、肝心のグラフが描かれません。どのように改善するべきかお教え願いたいです。。。

返信
1. wat より:
  
  2022年12月15日 10:08 PM
  
  ご訪問ありがとうございます。
  そのコードをコピペしてこちらで実行してみました。
  以下のコードが抜けているようですが、Masa様のコードにはありますでしょうか？
  sol = odeint(func, state0, t, args=(m, k, c))
  
  また、state0（初期変位、初速度）が共に0になっています。
  この状態だと解析結果は全て0（振動しない）になります。
  こちらでは以下のように条件を変更することで減衰自由振動の波形が描かれました（初期変位を1にする＋時間分解能を少し細かくする）。
  state0 = [1.0, 0.0]
  t0 = 0
  tf = 0.5
  dt = 0.005
  
  以上ご確認いただければと思います。
  よろしくお願い致します。
  
  返信

Pythonで1自由度減衰系の自由振動シミュレーション

1自由度減衰系とは？

Pythonによる振動シミュレーションのコード

全コード