
Pythonとかよくわからないけど、今すぐ逆フーリエ変換をしなくてはいけない人向けの記事です。過去記事のフーリエ変換した結果を使って、振幅と位相情報から時間波形を再生する方法を解説します。入力と出力は全てcsvファイルで統一しました。
こんにちは。wat(@watlablog)です。ここではただcsvファイルから逆フーリエ変換する方法を紹介します!
この記事の対象者
とにかく逆フーリエ変換したい人
この記事は、「細かい事は良い!とにかく爆速で逆フーリエ変換がしたいんだ!」という方を対象としています。
自分で逆変換のコード書いてみたけどなぜか元波形を復元できない…。
気軽に逆フーリエ変換して時間波形を取得したいけど適当なツールがない!
…という人々の助け舟になればという思いで記事にしています。もちろんあわよくばPythonユーザを増やしたいという気持ちも半分ほどあります!
「Python、何それ?」な人
この記事ではPythonというプログラミング言語を使って逆フーリエ変換を行います。とにかく逆フーリエ変換したい人にとって言語はどうでもよいと思いますが、ここでは誰が何と言おうとPythonで行います。
でも安心して下さい。このページでは当ブログでこれまで扱ったPythonインストール方法の記事リンクから説明しますので、WindowsかMacのPCさえ持っていれば、Pythonに関して全く知識がない人も最後まで読み進める事が出来ます。
さらに、プロキシ設定に阻まれてライブラリインストール出来ない人も対象にしています。インターネットに接続できて、PyPIにアクセスできれば問題ありません。
もちろん全て無料です。
フーリエ変換についてもう少し知りたい方は「PythonでFFT実装!SciPyのフーリエ変換まとめ」をご覧下さい。
また、逆フーリエ変換は「PythonでFFTとIFFT!逆フーリエ変換で時間波形を作る」や「Pythonでヒルベルト変換!時間波形の包絡線を求める方法」でも説明しています。参考までに。
但し、上の記事を参考にしても実データを逆フーリエ変換した時にうまくいかない人が多く出ると想定されます。本記事では最低限その部分の説明もしてみたいと思います。
より詳しく知りたい方は
フーリエ変換や逆変換を式ベースで理解したい人は、まずはこちらの参考書をオススメします。信号処理の基本から学べ、図が豊富にあるので初学者にやさしいです。
この記事の目標
csvファイルに記録した振幅と位相から時間波形をつくる
ここでは下図の周波数波形が記録されたcsvファイルを逆離散フーリエ変換(IDFT)します。csvファイルは振幅と位相の情報に分けて信号順で並んでいます。信号数はいくつでも構いません。振幅N個→位相N個の順で並べておいて下さい。
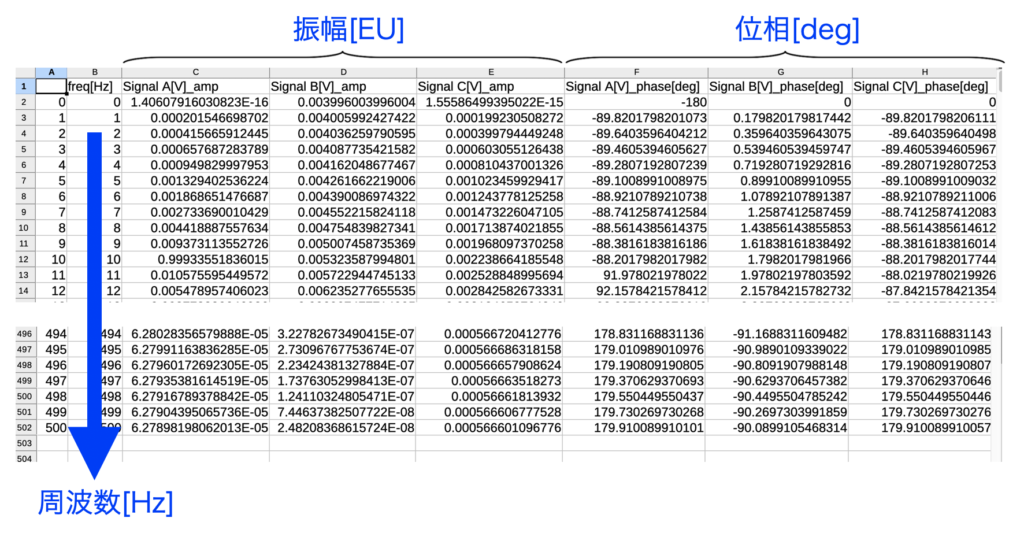
A列にインデックス欄がある事に注意して下さい。このcsvファイルのフォーマットは「ただPythonでcsvから離散フーリエ変換をするだけのコード」で紹介したコードによって出力されるフォーマットになっています。
検証済の動作環境
PC
僕は以下のWindows環境、Mac環境で本記事のコードを動作検証しています。Linuxやその他OSは対象としていません。
| Windows | OS | Windows10 64bit |
|---|---|---|
| CPU | 2.4[GHz] | |
| メモリ | 4[GB] |
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
(そろそろメモリが乏しくなってきたので新しいの欲しい)
Python環境
この後説明するPython環境に関するバージョン情報は以下表に示す通りです。おそらく最新バージョンでも動くと思いますが、検証したのは下の環境のみ。とにかくはやく逆フーリエ変換したい場合は揃えておくのが無難かと思います。
PythonはPython本体、PyCharmはプログラムを記述して実行したりデバッグしたりする統合開発環境(IDE)、Numpy・Scipy・Pandas・matplotlibはPythonにインポートして使う便利な外部ライブラリです。
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| Scipy | 1.7.1 |
| Pandas | 1.3.1 |
| matplotlib | 3.4.3 |
以上の前置きを確認したら、早速環境構築をしていきましょう!環境が既に構築されている人はコード部分までスクロールして下さい。
環境構築
Pythonのインストール
はじめにプログラミング言語であるPythonをインストールしましょう。
PythonのインストールにはAnacondaを推奨する書籍やサイトが沢山ありますが、2021年現在Anacondaは商用利用に制限がかかっているようです。それ以外にも色々面倒な管理となりそうであるため、筆者はAnacondaを使っていません(いちいちライブラリをインストールするのは面倒ですが)。
インストールの方法はWindowsとMacで以下の記事をご確認下さい。
Windows版:「Pythonのインストール方法とAnacondaを使わない3つの理由」
Mac版:「macOSにPython3をインストールする方法をまとめてみた」
そのうちもっと良い環境構築方法も試してみたいと思います(Dockerとか?)
統合開発環境(IDE)のインストール
コードを打ち込んでプログラムを実行するだけならテキストエディタを使ってコマンドプロンプトやターミナルで実行する方法でも十分ですが、デバッグやコード記述補助機能を利用するためには統合開発環境(IDE)を使うのが良いです。
こちらも以下のWindowsとMacで記事を用意していますので、参照しながらインストールしてみて下さい。
Windows版:「Pythonの統合開発環境(IDE)はPyCharmで良い?」
Mac版:「macOSにPython統合開発環境PyCharmをインストール」
外部ライブラリのpipインストール
pip概要と外部ライブラリのインストール方法
先ほど紹介したNumpyやScipyといった外部ライブラリはpipインストールするのが一般的です。
pipについての概要は「Pythonのパッケージ管理ツール pip の使い方とコマンド集」、Windows版とMac版のコマンドの違いは「独断!Pythonでpipインストールしたい外部ライブラリまとめ」をご確認下さい。
プロキシエラーになる場合
環境によってはもしかするとpipインストール時にプロキシエラーが発生するかも知れません。
PyPIにアクセスできるインターネット環境をお持ちであれば、「pip installでプロキシエラーになる問題を解決する方法」に記載の方法で解決可能です。
こんな事で諦めるのはもったいないです。
csvを逆離散フーリエ変換するPythonコード
準備するcsvファイル【ダウンロード可】
ここからはいよいよコードを使って逆フーリエ変換をしてみます。
まずはサンプルのcsvファイルとして以下の「fft.csv」をダウンロードしてみて下さい。
ただ、書き換える時はエンコードを「SHIFT-JIS」にする事を忘れずに。もし「UTF-8」で作ってもコードの方を変更すれば大丈夫ですが。
ちなみに、上記のcsvファイルは以下のsignals.csvを離散フーリエ変換したものです。下の方に検証用でこちらのファイルを使って波形が重なっているかをみますので、同じく検証したい方はこちらのファイルもダウンロードしてみて下さい。
全コード【コピペ・2次利用可】
以下にcsvに記録した振幅と位相情報から逆フーリエ変換するだけの全コードを示します。このコードを実行するとifft.csvというファイルが生成されます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
import numpy as np from scipy import fftpack import pandas as pd import matplotlib.pyplot as plt # csvから列方向に順次逆フーリエ変換を行い保存する関数 def csv_ifft(in_file, out_file): df = pd.read_csv(in_file, encoding='SHIFT-JIS') # ファイル読み込み(0列にインデックスがある事に注意) n = int((len(df.T) - 2) / 2) # 信号数=(振幅数と位相数)/2 f0 = df.T.iloc[1, 1] # 周波数刻み # データフレームを初期化 df_time = pd.DataFrame() df_ifft = pd.DataFrame() # 列方向に順次逆フーリエ変換(IDFT)をするコード ifft_time_list = [] for i in range(n): # 振幅と位相を抽出 amp = df.T.iloc[i + 2] amp *= len(amp) phase = np.radians(df.T.iloc[i + 2 + n]) # 実部と虚部を計算 Re = amp * np.cos(phase) Im = amp * np.sin(phase) # 鏡像部分を作成 Re_inv = Re[1:][::-1] Im_inv = Im[1:][::-1] # 複素数を構成(0Hzで実部は線対称、虚部は点対称なので符号に注意) comp_add = np.concatenate([(Re + (1j * Im)), (Re_inv + (-1j * Im_inv))]) # 逆フーリエ変換 ifft_amp = fftpack.ifft(comp_add).real ifft_time_list.append(ifft_amp) df_time[df.columns[i + 2] + '_ifft'] = pd.Series(ifft_amp) # 列名と共にデータフレームに時間波形計算結果を追加 # 周期T、時間刻みdt、時間軸を生成 T = 1 / f0 dt = T / len(ifft_amp) time_axis = np.arange(0, T, dt) # csvファイルに保存 df_ifft['freq[Hz]'] = pd.Series(time_axis) df_ifft = df_ifft.join(df_time) df_ifft.to_csv(out_file) return df, ifft_time_list, time_axis # 関数を実行してcsvファイルを逆フーリエ変換するだけの関数を実行 df, ifft_time_list, time_axis = csv_ifft(in_file='fft.csv', out_file='ifft.csv') |
signals.csv(元の時間波形)を用意し、以下のコードを追加することで、元の波形と逆フーリエ変換した後の時間波形を重ねて表示する事ができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# ここから先は検証用(信号の数だけ元波形と比較して重なるかチェック) # signals.csvを用意する必要がある。 for i in range(len(ifft_time_list)): # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude[EU]') # スケールの設定をする。 #ax3.set_yscale('log') #ax3.set_xscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 df_time = pd.read_csv('signals.csv', encoding='SHIFT-JIS') data = df_time.T.iloc[i+1] # フーリエ変換するデータ列を抽出 ax1.plot(time_axis, data, label='Original_' + df.columns[i + 2], lw=4) ax1.plot(time_axis, ifft_time_list[i], label='IDFT_' + df.columns[i + 2], lw=1) ax1.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
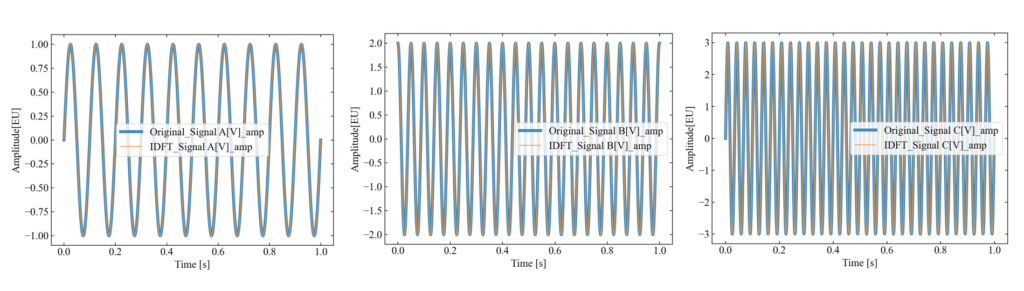
プロットは1波形毎に表示されます。以下が結果の例です。
本コードで計算した結果が元の時間波形と重なる様子が確認できます。
補足
振幅と位相を複素数にする時のポイント
振幅と位相・実部と虚部の関係
おそらく多くの分析に関する実務(実験結果の周波数分析等)において、フーリエ変換を行った後、そのまま複素スペクトルで評価する事はせず振幅\(A\)と位相\(\theta\)情報に分離する事でしょう。
これは振幅と位相が実際の振動現象を分析するのに複素数のスペクトルよりも便利な事が要因ですが、逆フーリエ変換を行うためには再び複素数に戻す必要があります。
下図の関係から振幅と位相・実部と虚部は相互に変換が可能です。
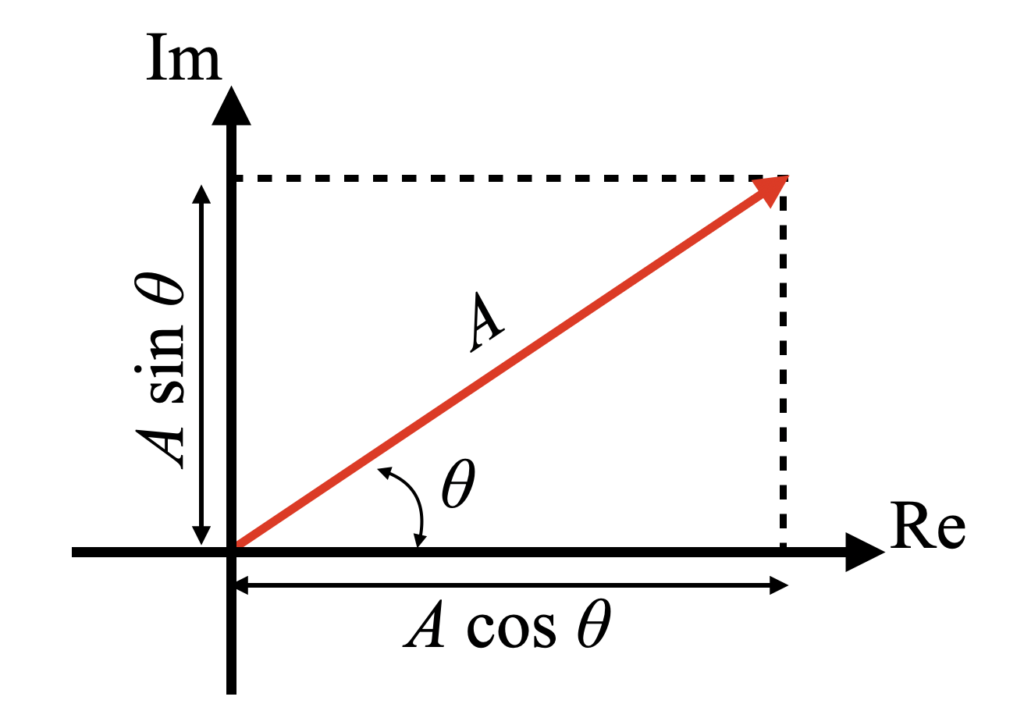
特にこれで問題はないように思いますが、以下の注意点があります。
実部と虚部のミラーリングをコーディングする必要がある
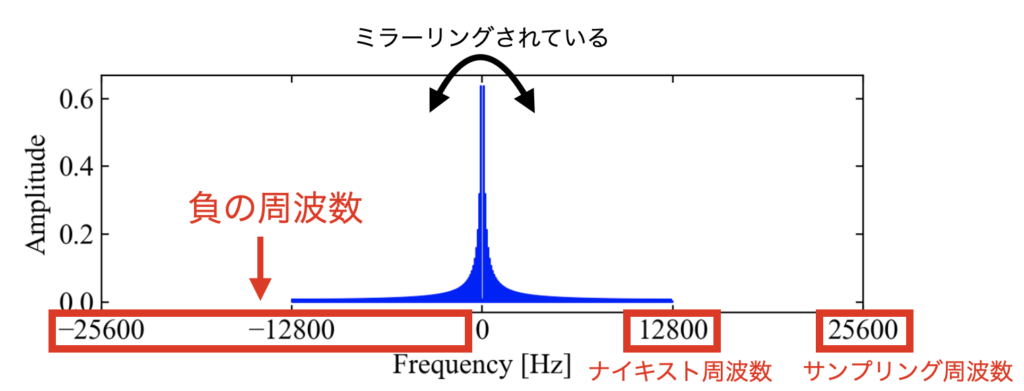
実際に時間波形をフーリエ変換して振幅成分を確認すると、負のナイキスト周波数から正のナイキスト周波数までデータが計算されます(下図)。
振幅情報は図のように反転された様相を示し、これを鏡像やミラーリングと呼んだりします。
(細かい定義では、分析する信号が実数の場合…といった条件が付くのですが、工学分野でフーリエ変換する場合、扱う信号は実数がほとんどだと思いますので、ここでは全ての場合で議論しません。)
Pythonのscipy.fftpack.fftで計算するとデータの並びとしては下図のようになります。
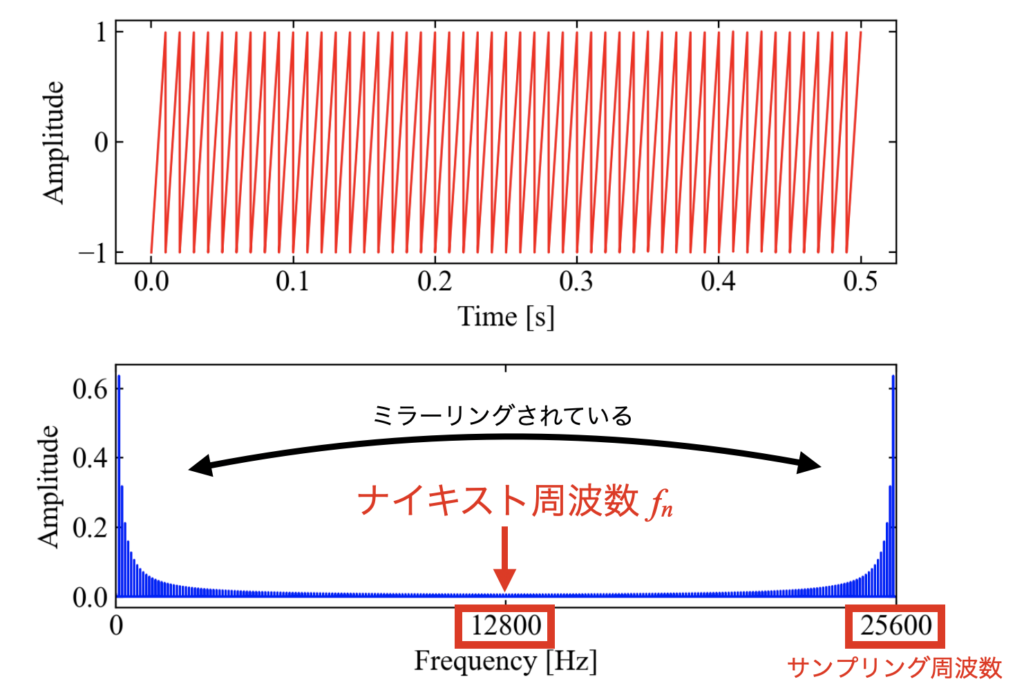
scipy.fftpack.fftfreqで周波数軸を計算すると、データの後半に負の周波数が入っている事がわかりますが、scipy.fftpack.ifftで逆フーリエ変換を行う場合はこのデータの並びを揃えておく必要があります。
以下は正弦波のフーリエ変換結果を、実部と虚部でプロットした結果です。このように、実部は0[Hz]部分で線対称に折り返されますが、虚部は0[Hz]で点対称に折り返される事に注意が必要です。
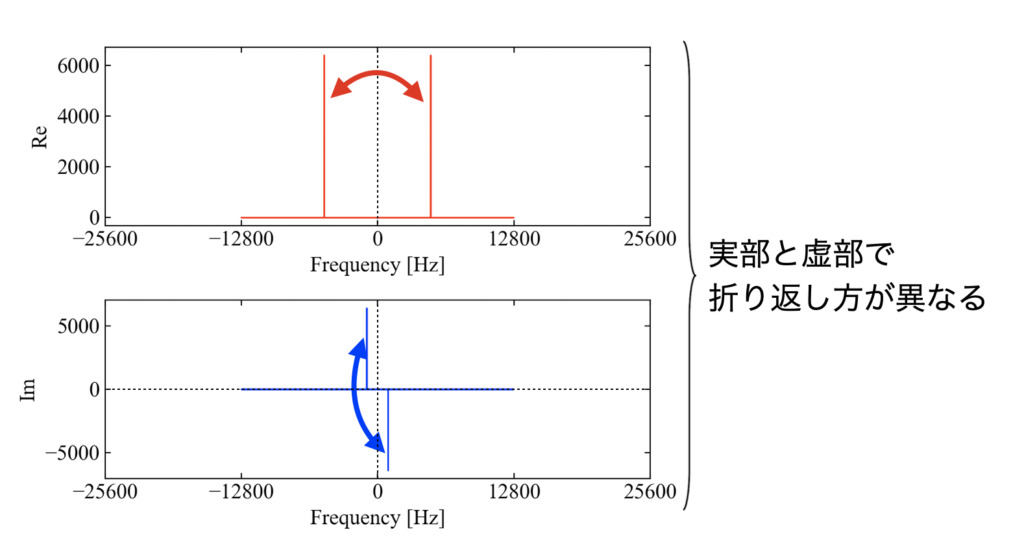
この事と、scipyのフーリエ変換の並び順に注意して複素データを構成している部分が以下のコードになります。
|
1 2 3 4 5 6 7 8 9 10 |
# 実部と虚部を計算 Re = amp * np.cos(phase) Im = amp * np.sin(phase) # 鏡像部分を作成 Re_inv = Re[1:][::-1] Im_inv = Im[1:][::-1] # 複素数を構成(0Hzで実部は線対称、虚部は点対称なので符号に注意) comp_add = np.concatenate([(Re + (1j * Im)), (Re_inv + (-1j * Im_inv))]) |
多くの商用計測ソフトはデータがナイキスト周波数までしかエクスポートできないと思いますので、これらの特性を知らないと任意のデータで逆フーリエ変換する事ができません。
※ちなみに上記データの並び順を変えたり、虚部も線対称にしたりすると復元される時間波形が特徴的な変化をするので、興味のある方は是非お試し下さい。
まとめ
ここではcsvファイルで記録された振幅と位相情報を持つ周波数波形の逆フーリエ変換を行い、時間波形を復元するコードを紹介しました。
逆フーリエ変換の場合は実部と虚部の扱いに特に注意が必要だという事も理解する事ができました。
csvでフーリエ変換・逆変換・デジタルフィルタ処理をする方法
時間波形をフーリエ変換する方法、時間波形にデジタルフィルタをかける方法、周波数波形を逆フーリエ変換する方法が全てcsv間でできるようになりました。以下にリンクをメモしますので、是非分析業務にお役立て下さい。
時間波形をフーリエ変換する方法
ただPythonでcsvから離散フーリエ変換をするだけのコード
時間波形にデジタルフィルタをかける方法
ただPythonでcsvからデジタルフィルタをかけるだけのコード
周波数波形を逆フーリエ変換する方法
※本記事。
Pythonによる逆フーリエ変換をcsvで実施できるようになりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
