工業製品で扱う振動というのはとにかく抑えたいものです。ここでは制振技術の一つであるパッシブ型のダイナミックダンパーについて解説し、Pythonによるシミュレーションでパラメータスタディを行う方法を紹介します。
こんにちは。wat(@watlablog)です。今回は制振技術であるダイナミックダンパーについてまとめ、Pythonでシミュレートする方法を紹介します!
ダイナミックダンパーの概要
振動が問題になるという事
制振技術について紹介する前に、振動が問題になるという事の意味をおさらいしておきましょう。
楽器等音を出すための機器、製品にとって振動はより大きくしたり、効率をよくしたり、音色を調整したりといった事が付加価値を高めるために行われる設計行為です。
しかしその他のモータ等の回転機、高層ビル、橋といった工業製品にとって振動は製品の信頼性を損なう方向に作用し、大抵の技術者に嫌われる存在となっています。
機械力学を学んだ方であれば、タコマ橋の崩壊の話が有名でしょうか?ご存知で無い方は以下のYoutube動画をご覧下さい。
風が橋の上下にカルマン渦を発生させ、その周波数が橋の固有振動数と一致し共振してしまった事が原因と言われています(共振怖い…)。
共振によって発生するエネルギーは莫大で、堅牢な構造物でさえも疲労破壊してしまう事があります。
固有値解析による共振設計
このような振動による問題を起こさないために、通常は共振を避ける固有値の設計を行います。その際は固有値解析という手法を用いて設計検討がされます。
固有値解析について当ブログでは「Pythonで多自由度系の固有値解析!固有振動数とモードを計算」でPythonコードを紹介していますので、ご興味のある方は是非参考にして下さい。
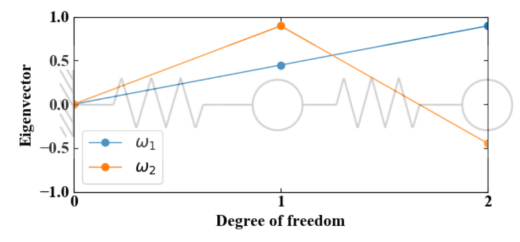
固有値解析をする事で、固有振動数はもちろんの事、以下の図のように固有ベクトル(振動モード)を知る事ができ、どこの強度を高めれば良いかのヒントを得る事が出来ます。
発生した振動を抑える制振技術
固有値解析を行って共振させない設計を行う事は基本なのですが、実際の機械は様々な周波数に固有振動数を持っています。
そのため、固有値があっても振動を抑える事ができる制振技術というのが、古くから研究されてきました。これから制振技術について理解を深める前に、周波数応答関数(FRF)の計算をおさらいしましょう。
当ブログでは「Pythonで伝達関数!2つの信号の周波数応答関数を計算する方法」で振動モデルにおけるFRFを計算してみました。
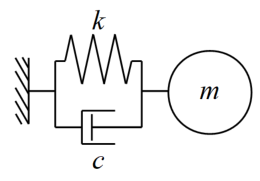
例えば以下の1自由度モデルについて、質点に外力が加わった時のFRFを計算してみます。
パラメータは適当ですが、結果は下図になります。右下のプロットがFRFです。
この右下のFRFは各周波数で1[N]の加振(Excitation)が発生したら、何[m]振動するかを意味しており、振動感度とも呼ばれます。
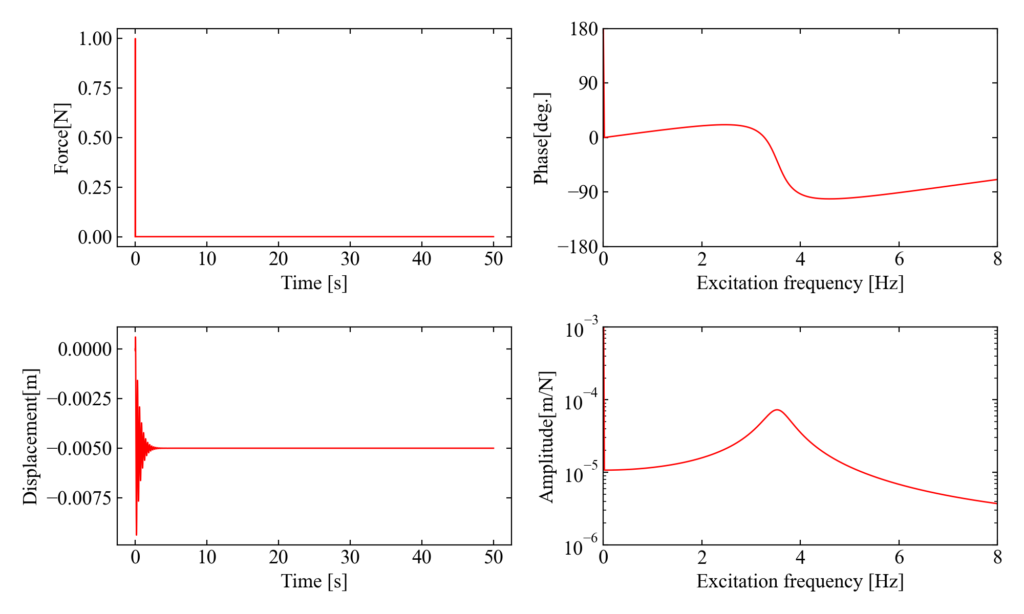
自由度が1つだけのモデルだと共振ピークが一つ発生している事がわかります。
しかし、実際の構造物のFRFイメージを下図に示します。このように実際の物は製品の動作周波数帯域全域で様々な固有振動モードを持つ事がざらです。これらを全て無くそうとすると、オリハルコンとかアダマンタイトとかで物を作らないといけなくなり、それはちょっとハードルが高くなります。
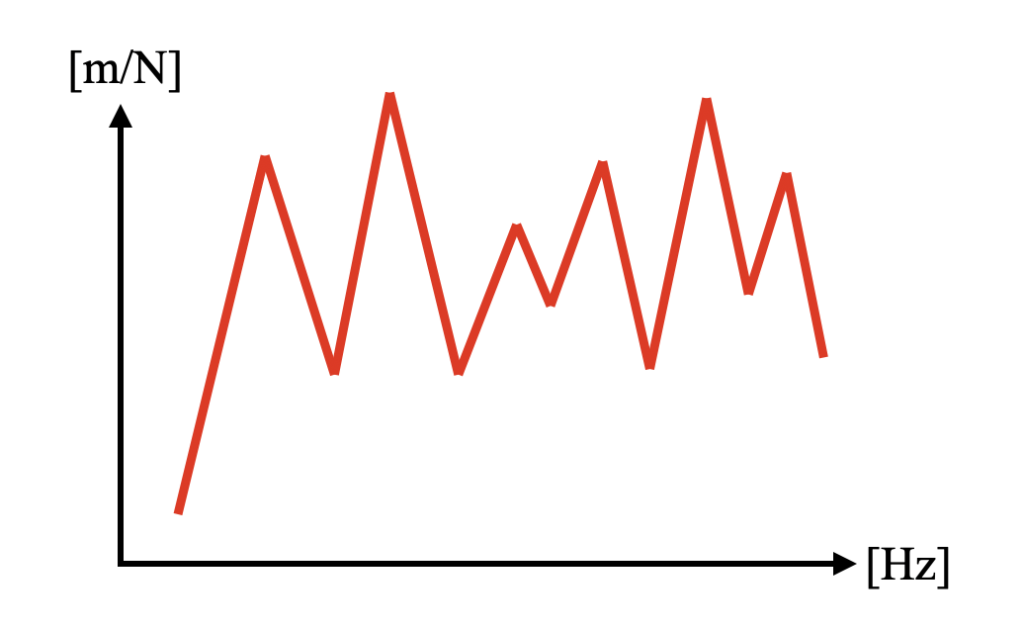
固有値が存在するのは仕方無いのですが、できれば下図の青波形のように山を潰して、例え共振したとしても悪影響をできるだけ小さくしたいというのが理想です。
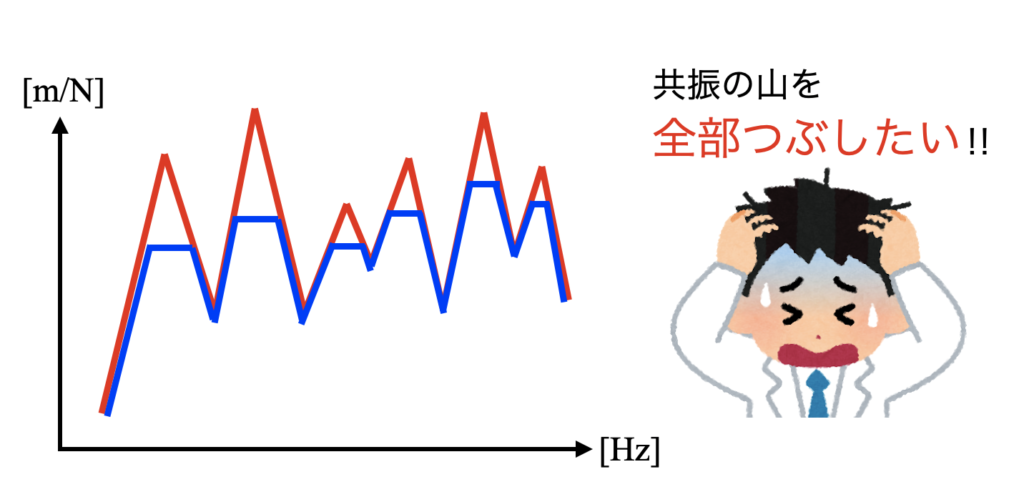
そんな都合の良い事…を研究している分野が制振技術の分野なのです。
ダイナミックダンパーとは?
ダイナミックダンパー(Dynamic damper)とは、日本語で動吸振器と呼び、先ほどまで説明していた振動を抑えるための機器、つまり制振器の一つです。
まずは以下の1自由度の振動モデルで考えてみましょう。
このモデルの質点にハンマで叩いたようにインパルス外力を加えると、質点は減衰自由振動します。これを主振動系と呼びます。
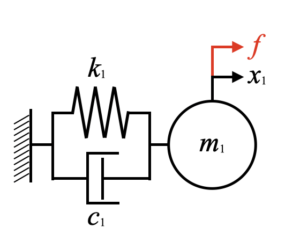
ダイナミックダンパーの付け方は実は様々あるのですが、最も有名なのが下図です。
この図は主振動系にもう一つばねマスダンパーを取り付け、2自由度にしたモデルです。この後付けした振動系は主振動系によって振動させられるため、従振動系と呼び、パラメータをうまく調整してあげる事でダイナミックダンパーとして作用するようになります。
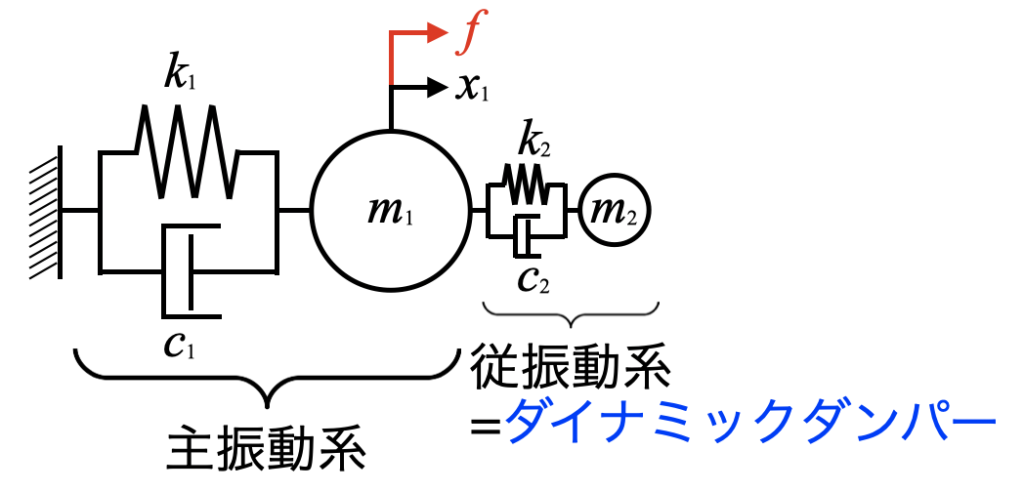
本記事ではPythonを使ってこの従振動系のシミュレーションを行い、どのような振る舞いをしていくかを観察する事を行います。
このような主振動系に従振動系を取り付けてダイナミックダンパーとする物はパッシブ型(受動型)に分類されます。
ダイナミックダンパーには固定面利用型、質量慣性力利用型(上の図)、相互反力利用型と色々なタイプがあり、パッシブ型以外にも制御を入れたアクティブ型、セミアクティブ型、組み合わせによるハイブリッド型と多岐に渡る種類があります。
この記事では上の図で示すパッシブ型、質量慣性力利用型に相当するモデルで検討していきますが、面白いのでご興味ある方は是非調べてみて下さい。
参考文献
詳細の理論はこのようなブログではなく、専門書を読んだ方が良いと思うため、ここではオススメの書籍を紹介するだけに留めます。

僕はダイナミックダンパーを勉強するためにこの本を購入しました。この本はタイトルからわかるように丸々1冊が動吸振器について書かれており、パッシブ系やアクティブ系の理論、その応用方法も書いてあります。
ダイナミックダンパーを設計する人必携…と思いますが、残念ながらこの記事を書いている現在Amazonにも楽天にも取り扱いがなく、リンクを紹介する事ができませんでした。
書店で見かけたら是非お手にとってみて下さい。
長々と書いてしまいましたが、これからいよいよPythonでダイナミックダンパーの振る舞いを遊びながら観察、コーディングしていきます!
Pythonでダイナミックダンパーをシミュレーションするコード
事前準備
4次のRunge-Kutta法コードを別ファイルで用意する
まずは過渡解析(時間波形上で応答を計算する解析)部分が長いので、別ファイルにします。
以下のコードは「Pythonで伝達関数!2つの信号の周波数応答関数を計算する方法」や「Pythonの4次ルンゲ・クッタ法で多自由度連成振動を解く方法」で紹介したコードとほぼ同じですが、そちらのコードが2自由度専用であったのに対し、1自由度でも2自由度でも(おそらくN自由度でも)対応できるようにちょっと改善しました。
このコードを丸々「transient.py」という.pyファイルにしておきます。sim()にはメインファイルで作る質量、剛性、減衰マトリクスを渡す仕様にしました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import numpy as np # 運動方程式を関数として定義 def f(x, v, f, M, C, K): M_inv = np.linalg.inv(M) # 質量マトリクスの逆行列 F = np.zeros(len(M)) # 外力ベクトルの初期化 F[0] = f # 1自由度目に外力を設定 # 減衰強制振動モデル y = np.dot(M_inv, F) - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y # シミュレーションを4次のRunge-Kutta法で実行する関数 def sim(M, C, K): # 解析条件 t0 = 0.0 # 開始時間 t1 = 40.0 # 終了時間 dt = 1e-3 # 時間刻み # 初期条件 x0 = np.zeros(len(M)) # 初期変位[m] v0 = np.zeros(len(M)) # 初期速度[m/s] x, v = x0, v0 # 初期値に設定 t_axis = np.arange(t0, t1, dt) # 時間軸 x_sol = [] # 初期化x(変位)配列 v_sol = [] # 初期化v(速度)配列 # インパルス波形を加振力に設定 force = np.zeros(len(t_axis)) force[1:2:1] = 1 # 4次のRunge-Kutta法による数値解析(外力成分を離散1D波形から抽出するバージョン) iteration = 0 for t in t_axis: # 1自由度目の変位と速度をappend x_sol.append(x[0]) v_sol.append(v[0]) # イタレーションをモニタ print('iteration=', iteration,'time=', t, force[iteration]) # Runge-Kuttaのメイン k11 = f(x, v, force[iteration], M, C, K) * dt k12 = v * dt k21 = f(x + dt / 2, v + k11 / 2, force[iteration], M, C, K) * dt k22 = (v + k11 / 2) * dt k31 = f(x + dt / 2, v + k21 / 2, force[iteration], M, C, K) * dt k32 = (v + k21 / 2) * dt k41 = f(x + dt, v + k31, force[iteration], M, C, K) * dt k42 = (v + k31) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 iteration += 1 return force, x_sol, dt, t_axis |
メインコード:1自由度モデルでコードの確認
まずは1自由度でコードの確認をしていきます。モデル図は以下。今回は各パラメータも重要なので、数値を書いておきます。
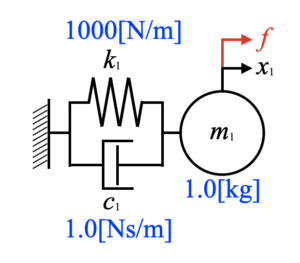
以下がメインのコード全文です。関数としてモデル生成、固有値解析、周波数応答関数計算を含ませています。import transientで先ほど別ファイルにしたコードを使います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt import transient def model_1dof(): # 質量m・減衰c・剛性kの集中定数を設定する m1 = 1 c1 = 1 k1 = 1000.0 # マトリクス化 M = np.array([[m1]]) C = np.array([[c1]]) K = np.array([[k1]]) return M, C, K # 固有値解析を計算する関数 def eigen(M, K): # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort # 周波数応答関数(FRF)を計算する関数 def frf(input, output, samplerate): fft_i = fftpack.fft(input) # 入力信号のフーリエ変換 fft_o = fftpack.fft(output) # 出力信号のフーリエ変換 # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) # FRFの振幅成分 amp = amp / (len(input) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(h_io.imag, h_io.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(input)) # 周波数軸を作成 return h_io, amp, phase, freq # サンプル信号を準備する(別ファイルで作成したsimulation.pyのsim()関数で計算) # ①:1自由度振動系の過渡応答解析 M, C, K = model_1dof() eigen_value1, eigen_vector1 = eigen(M, K) input, output, dt, t_axis = transient.sim(M, C, K) print(eigen_value1) # FRFを関数を実行して計算 h_io, amp, phase, freq = frf(input, output, 1 / dt) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 6)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(222) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(224) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') # スケールの設定をする。 ax3.set_xlim(0.1, 100) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax3.set_xscale('log') ax4.set_xlim(0.1, 100) ax4.set_ylim(1e-8, 1e-3) ax4.loglog() # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='1dof', lw=1, color='red') ax2.plot(t_axis, output, label='1dof', lw=1, color='red') ax3.plot(freq, phase,label='1dof', lw=1, color='red') ax4.plot(freq, amp, label='1dof', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
メインコードを実行すると、以下の結果を得ます。今回減衰は低く設定し、鋭いピークが出るようにしてみました。固有値解析の結果は約5[Hz]を示しています。

ダイナミックダンパーの振る舞い観察
何も考えないで2自由度化してみると…
ダイナミックダンパーを実装していきますが、まずは何も考えないで、下図のように主振動系と同じパラメータをそのまま従振動系にも割り当ててみましょう。普通はこんな設定はしませんが…。
モデルの加振はあくまで\(m_{1}\)に与えています。\(m_{2}\)は受動振動するだけ。
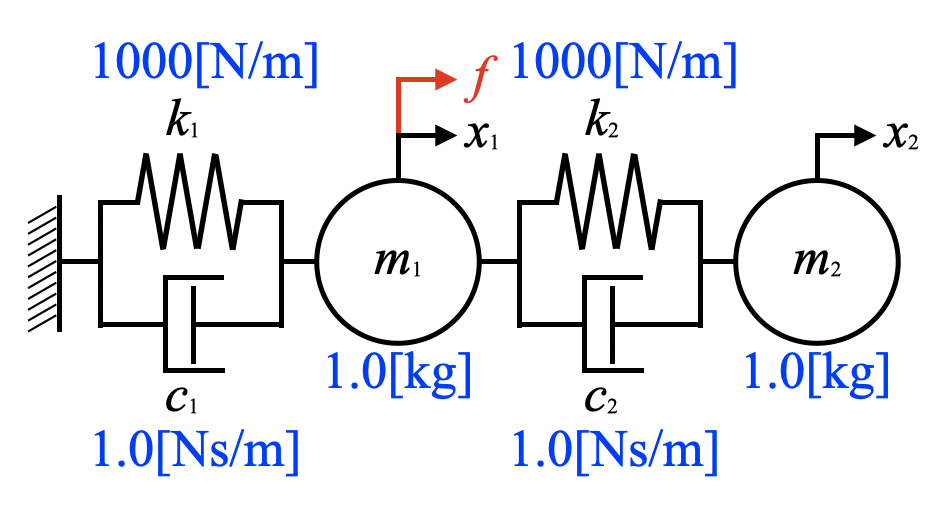
メインコードを編集します。関数としてmodel_dynamic_damper()を追加し、固有値解析、周波数応答関数計算を2回やってグラフで比較するというコードです。1自由度でも2自由度でも同じsim()を使えるように今回変えたのでした。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt import transient def model_1dof(): # 質量m・減衰c・剛性kの集中定数を設定する m1 = 1 c1 = 1 k1 = 1000.0 # マトリクス化 M = np.array([[m1]]) C = np.array([[c1]]) K = np.array([[k1]]) return M, C, K def model_dynamic_damper(): # 質量・減衰・剛性の集中定数を設定する m1 = 1 m2 = 1 c1 = 1 c2 = 1 k1 = 1000.0 k2 = 1000.0 # 振動評価指標を計算 mu = m2 / m1 # 質量比 cc = 2 * np.sqrt(m2 * k2) # 臨界減衰係数 zeta = c2 / cc # 減衰比 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) return M, C, K, mu, zeta # 固有値解析を計算する関数 def eigen(M, K): # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort # 周波数応答関数(FRF)を計算する関数 def frf(input, output, samplerate): fft_i = fftpack.fft(input) # 入力信号のフーリエ変換 fft_o = fftpack.fft(output) # 出力信号のフーリエ変換 # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) # FRFの振幅成分 amp = amp / (len(input) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(h_io.imag, h_io.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(input)) # 周波数軸を作成 return h_io, amp, phase, freq # サンプル信号を準備する(別ファイルで作成したtransient.pyのsim()関数で計算) # ①:1自由度振動系の過渡応答解析 M, C, K = model_1dof() eigen_value1, eigen_vector1 = eigen(M, K) input, output, dt, t_axis = transient.sim(M, C, K) print(eigen_value1) # ②:①の結果にダイナミックダンパーを付けたモデルで過渡応答解析 M, C, K, mu, zeta = model_dynamic_damper() eigen_value2, eigen_vector2 = eigen(M, K) input2, output2, dt, t_axis = transient.sim(M, C, K) print(eigen_value2) # FRFを関数を実行して計算 h_io, amp, phase, freq = frf(input, output, 1 / dt) h_io2, amp2, phase2, freq2 = frf(input2, output2, 1 / dt) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 6)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(222) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(224) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') # スケールの設定をする。 ax3.set_xlim(0.1, 100) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax3.set_xscale('log') ax4.set_xlim(0.1, 100) ax4.set_ylim(1e-8, 1e-3) ax4.loglog() # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='1dof', lw=1, color='red') ax1.plot(t_axis, input2, label='2dof', lw=1, color='blue') ax2.plot(t_axis, output, label='1dof', lw=1, color='red') ax2.plot(t_axis, output2, label='2dof', lw=1, color='blue') ax3.plot(freq, phase, label='1dof', lw=1, color='red') ax3.plot(freq, phase2, label='2dof', lw=1, color='blue') ax4.plot(freq, amp, label='1dof', lw=1, color='red') ax4.plot(freq, amp2, label='2dof', lw=1, color='blue') ax4.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=10) ax4.text(0.11, 1e-4, '$\ \omega=$' + str(round(eigen_value2[0], 2)) + ', ' + str(round(eigen_value2[1], 2)), fontsize=10) ax4.text(0.11, 5e-5, '$\ \mu=$' + str(round(mu, 2)), fontsize=10) ax4.text(0.11, 2e-5, '$\ \zeta=$' + str(round(zeta, 2)), fontsize=10) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
下図が結果です。単純に同じパラメータで2自由度化すると、ピークが二つに割れました。個々の振動系だけでみれば同じ固有振動数になるわけですが、このように2モードが近接するとピークが割れます。まさに連成振動、って感じですね。
この図は全然制振したとは言えず、むしろピークがより大きくなってしまったという結果を意味しています。適当はダメ、という事ですね。
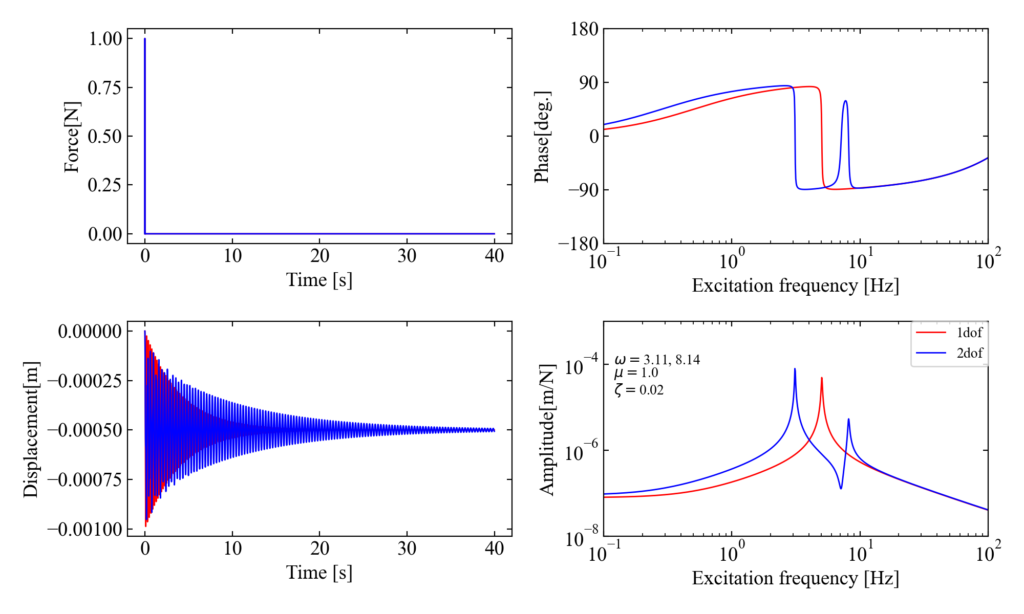
ちなみにFRFプロットの中に従振動系の固有振動数\(\omega\)、従振動系と主振動系の質量比\(\mu\)、従振動系の減衰比を記載しています。ダイナミックダンパーのパラメータ設計としてはこの辺が重要になってきます。
減衰比を振ってみると…
先ほどは主振動系と同じモデルをさらに追加してしまいましたが、制振したい対象と同じ質量を使った対策は中々とられません(コストもかかるので)。
次は以下のように従振動系の質量を主系の\(\frac{1}{10}\)にしてみます。さらに、ダイナミックダンパーは主系と連成させて作用するため、剛性\(k_{2}\)は主系の固有振動数を目掛けて調整します(この調整方法が良いわけではありません)。
この状態で減衰係数\(c_{2}\)を決めますが、今回は減衰比\(\zeta\)を振ってみます。
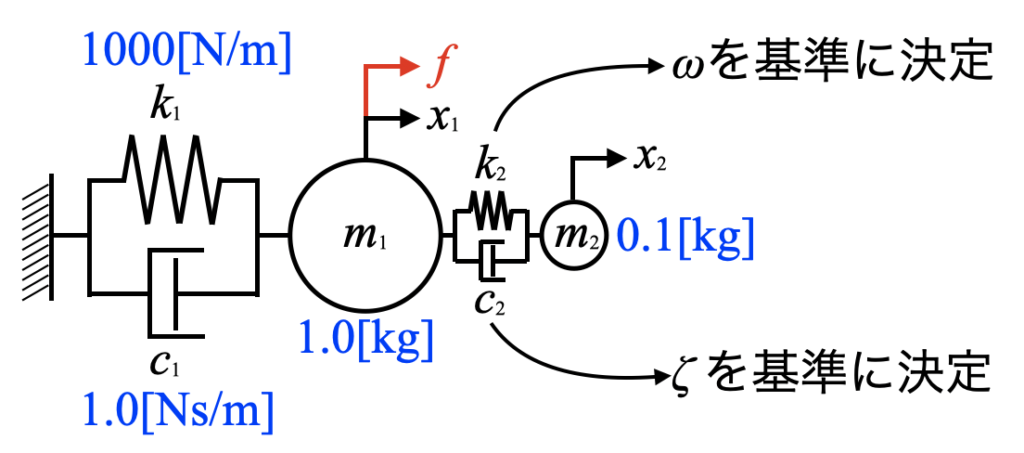
固有振動数を基準にした剛性は以下の式で求めました(ここは単なるトライです)。
また減衰係数は以下の式で算出しました。
減衰比を複数振って応答を比較するコードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt import transient def model_1dof(): # 質量m・減衰c・剛性kの集中定数を設定する m1 = 1 c1 = 1 k1 = 1000.0 # マトリクス化 M = np.array([[m1]]) C = np.array([[c1]]) K = np.array([[k1]]) return M, C, K def model_dynamic_damper(zeta): # 質量・減衰・剛性の集中定数を設定する m1 = 1 c1 = 1 k1 = 1000.0 m2 = 0.1 mu = m2 / m1 # 質量比 # 主振動系単体の固有振動数に合わせてk2を決定(減衰はここでは無視) omega = np.sqrt(k1 / m1) k2 = m2 * omega ** 2 cc = 2 * np.sqrt(m2 * k2) # 臨界減衰係数 # 減衰比を使って減衰係数を計算 c2 = zeta * cc M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) return M, C, K, mu # 固有値解析を計算する関数 def eigen(M, K): # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort # 周波数応答関数(FRF)を計算する関数 def frf(input, output, samplerate): fft_i = fftpack.fft(input) # 入力信号のフーリエ変換 fft_o = fftpack.fft(output) # 出力信号のフーリエ変換 # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) # FRFの振幅成分 amp = amp / (len(input) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(h_io.imag, h_io.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(input)) # 周波数軸を作成 return h_io, amp, phase, freq # サンプル信号を準備する(別ファイルで作成したtransient.pyのsim()関数で計算) # ①:1自由度振動系の過渡応答解析 M, C, K = model_1dof() eigen_value1, eigen_vector1 = eigen(M, K) input, output, dt, t_axis = transient.sim(M, C, K) print(eigen_value1) # ①のFRFを関数を実行して計算 h_io, amp, phase, freq = frf(input, output, 1 / dt) # ②:①の結果にダイナミックダンパーを付けたモデルで過渡応答解析(zeta違い) zeta_list = [0.01, 0.05, 0.1, 0.12, 0.4, 1.0] amps = [] for i in range(len(zeta_list)): M, C, K, mu = model_dynamic_damper(zeta_list[i]) input2, output2, dt, t_axis = transient.sim(M, C, K) h_io2, amp2, phase2, freq2 = frf(input2, output2, 1 / dt) amps.append(amp2) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax4 = fig.add_subplot(111) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') # スケールの設定をする。 ax4.set_xlim(0, 10) ax4.set_ylim(1e-7, 1e-4) ax4.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax4.plot(freq, amp, label='1dof', lw=1, color='black') for j in range(len(zeta_list)): ax4.plot(freq, amps[j], label='$\ \zeta=$' + str(zeta_list[j]), lw=1) ax4.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=16) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
上記コードを実行すると以下の結果を得ます。
減衰比の値によってピークの振幅成分が変化し、1自由度のみの場合と比べて低い振幅になっているものもあります。
但し、「あちらをへこませればこちらが立つ…」のような状況で、減衰比を思いっきりあげないと中々良い制振状態は得られそうもありません。
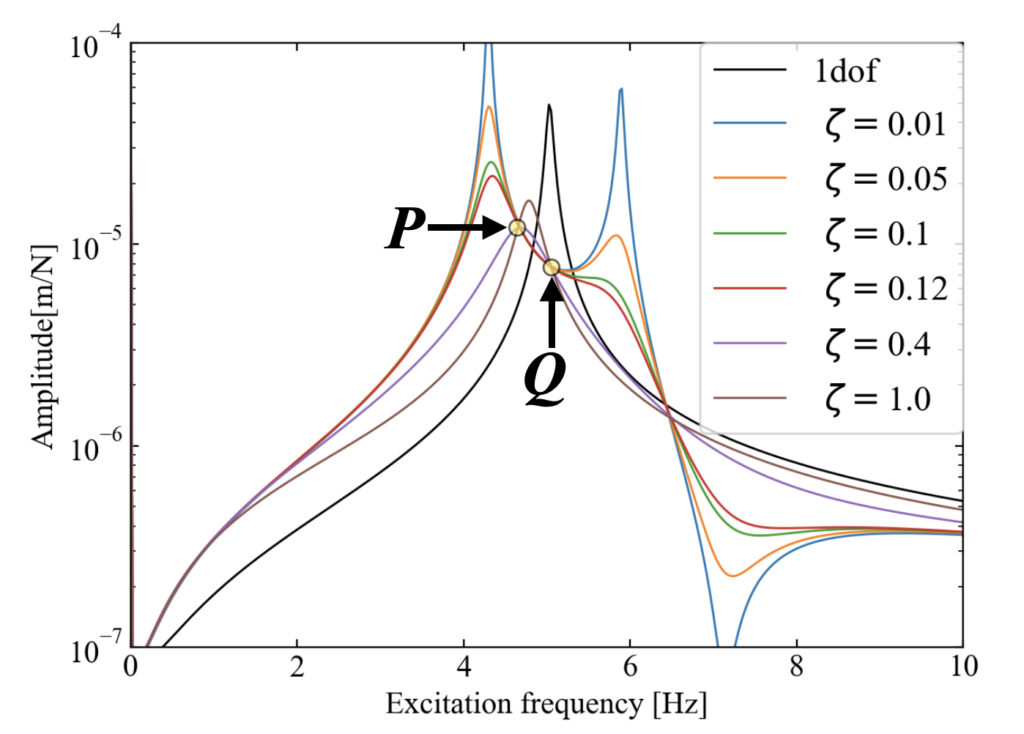
但し、臨界減衰係数が系の質量、剛性の影響も受けている事から、これらの複数パラメータを上手く調整する事ができれば、最適な制振機能を得る事が出来そうです。
実はプロットを眺めていると減衰比を振った波形全てが通る定点が2点あります。このPとQの2点の高さを揃えるように調整する定点理論というものがダイナミックダンパーにはあり、主の振動系に対して最適に同調し、最適な減衰比を求める事が主な制振設計となります。
主系に減衰が無い場合の最適条件コード
先ほどまでは素人の浅知恵で、あまり制振効果が得られないパラメータを選定してしまいました。今度はちょっと考えてみます。
教科書レベルだと以下の図のような主系に減衰の無い振動系にダイナミックダンパーとしてばねマスダンパー系を追加するのが第一歩のようです。
そしてダイナミックダンパーでは定点理論から導かれる最適同調条件(主系のエネルギーを同調振動して吸収する条件)と最適減衰条件(最も振動を抑えるダイナミックダンパーの減衰比)があります。
最適同調条件
主系に減衰が無い場合のダイナミックダンパーの最適同調条件は、質量比\(\mu\)と主系と従系の固有角振動数\(\omega_{1}\)、\(\omega_{2}\)が以下の式の関係になる条件を指します。
質量比\(\mu\)を任意の値に設計すると、次式で\(m_{2}\)が決定されます。
さらに求めた\(m_{2}\)を使う事で関係式から\(k_{2}\)を求める事が出来ます。
最適減衰条件
最適減衰条件はダイナミックダンパー\(\zeta_{opt}\)の減衰比が次式の関係になる条件です。質量比\(\mu\)は既にわかっているのでこれはそのまま演算で求める事ができます。
\(m_{2}\)と\(k_{2}\)がわかると、臨界減衰係数\(c_{c}\)との関係から\(c_{2}\)も求める事が可能です。
これで主系に減衰を含まない場合のダイナミックダンパーの最適条件が決まりました。
効果の確認
最適条件計算コード
メインコードの中で、model_dynamic_damper()を以下のコードのように変更して効果確認をしてみます。先ほどは手入力していたダイナミックダンパーのパラメータ\(m_{2}, c_{2}, k_{2}\)を上記関係式から自動決定しています(質量比のみ決めます)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def model_dynamic_damper(): # 質量・減衰・剛性の集中定数を設定する m1 = 1 c1 = 1 k1 = 1000.0 mu = 0.4 # 質量比を設計 m2 = mu * m1 # 従系の質量 omega = np.sqrt(k1 / m1) # 主系の固有振動数 omega2 = omega / (mu + 1) # 従系の固有角振動数 k2 = m2 * (omega / (mu + 1)) ** 2 # 従系のばね定数 zeta = (3 * mu) / np.sqrt(8 * (1 + mu) ** 3) # 最適減衰比 cc = 2 * np.sqrt(m2 * k2) # 従系の臨界減衰係数 c2 = zeta * cc # 従系の減衰係数 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) return M, C, K, m2, c2, k2 |
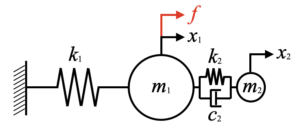
\(\mu=0.4\)
質量比\(\mu=0.4\)だとものすごい制振効果です(ここでは主系の減衰を小さくする事で元波形が「ほぼ」ずっと振動するようにしています)。
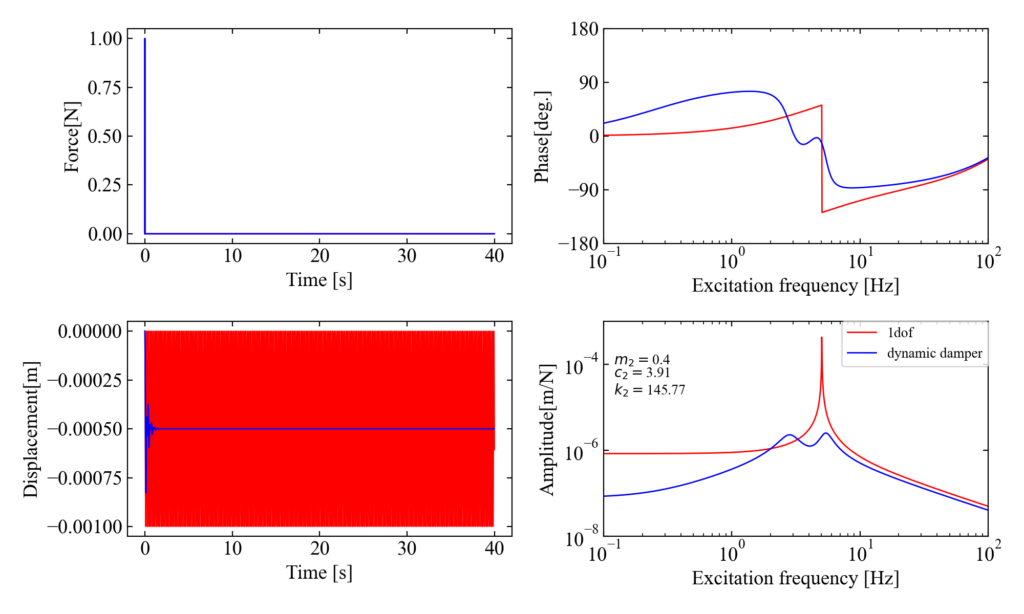
\(\mu=0.05\)
質量比\(\mu=0.05\)でも効果があるようです。小さい質量でも効果があれば、低コストで振動対策が出来てお得です。しかし初期振動が大きいのはなぜだろう?シミュレーションのせい?慣性?
おまけ:主系に減衰を入れる
主系に減衰を含まない系で構築された最適条件を、主系に減衰を入れた状態で使ってみた結果が以下。
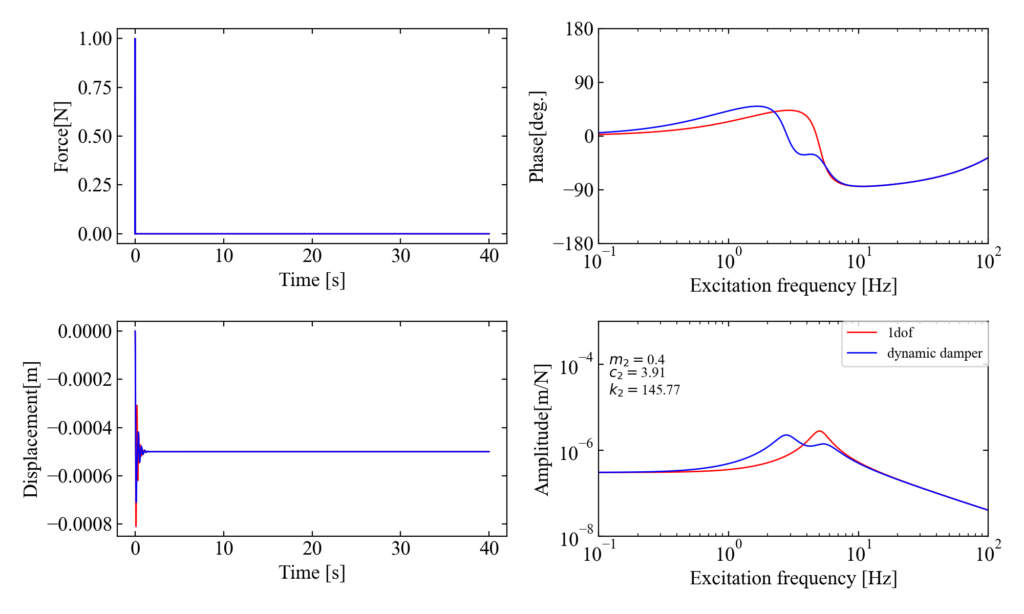
主系に減衰を含む場合の最適条件
主系に減衰を含む場合、つまり以下のモデルの場合の最適条件は少々やっかいです。
最適同調条件
しかし実用的な式を「池田 健, 五百井 俊宏, 減衰を有する振動系の最適調整法, 機論(第1部), Vol.43, No.369, pp.1707-1715(1977)」で研究され、主系の減衰比\(\zeta_{1}\)を使って以下の式のように最適同調が決まります(数値解析式のようです)。
\(k_{2}\)の求め方は先ほどと同様です。
最適減衰条件
最適減衰条件は次式です。こちらも実用のための数値解析式。\(c_{2}\)の求め方は先ほどと同様です。
効果の確認
最適条件計算コード
model_dynamic_damper()内の式を上記の物に変更したコードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
def model_dynamic_damper(): # 質量・減衰・剛性の集中定数を設定する m1 = 1 c1 = 1 k1 = 1000.0 zeta1 = c1 / (2 * np.sqrt(m1 * k1)) mu = 0.4 # 質量比を設計 m2 = mu * m1 # 従系の質量 omega = np.sqrt(k1 / m1) # 主系の固有振動数 # 最適同調のためのr r = 1 / ((mu + 1) - (0.241 + 1.74 * mu - 2.6 * mu ** 2) * zeta1 - (1.0 - 1.9 * mu + mu ** 2) * zeta1 ** 2) k2 = m2 * (omega * r) ** 2 # 従系のばね定数 # 最適減衰式 zeta2 = (3 * mu) / np.sqrt(8 * (1 + mu))\ + (0.13 + 0.12 * mu + 0.4 * mu ** 2) * zeta1\ - (0.01 + 0.9 * mu + 3 * mu) * zeta1 ** 2 cc = 2 * np.sqrt(m2 * k2) # 従系の臨界減衰係数 c2 = zeta2 * cc # 従系の減衰係数 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) return M, C, K, m2, c2, k2 |
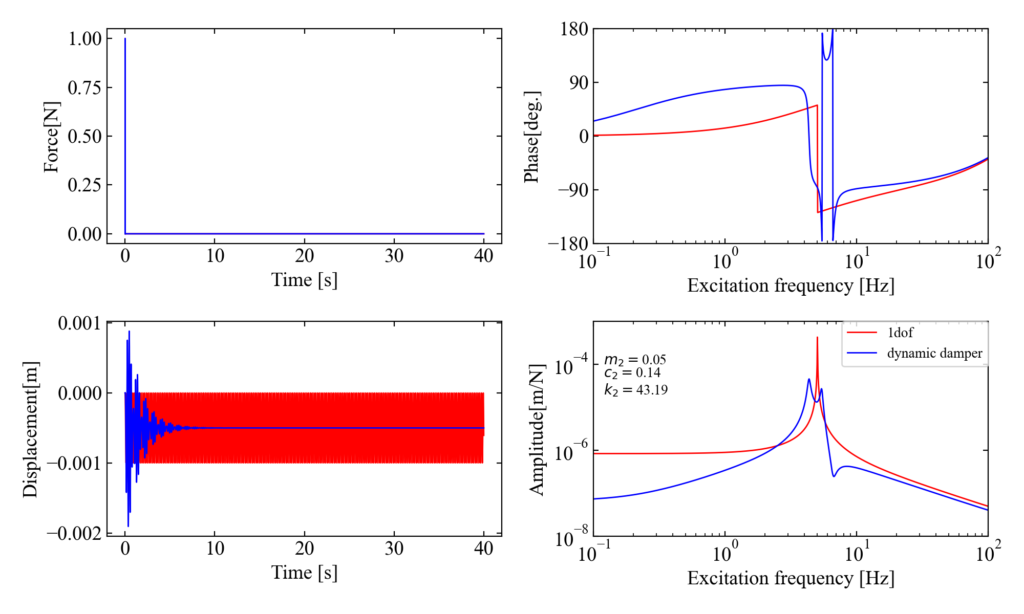
\(\mu=0.4, c_{1}=1\)
質量比\(\mu=0.4\)、減衰係数\(c_{1}=1\)として最適条件を計算したダイナミックダンパーの効果が以下です。先ほどまでよりもピークが滑らかになったみたいです。
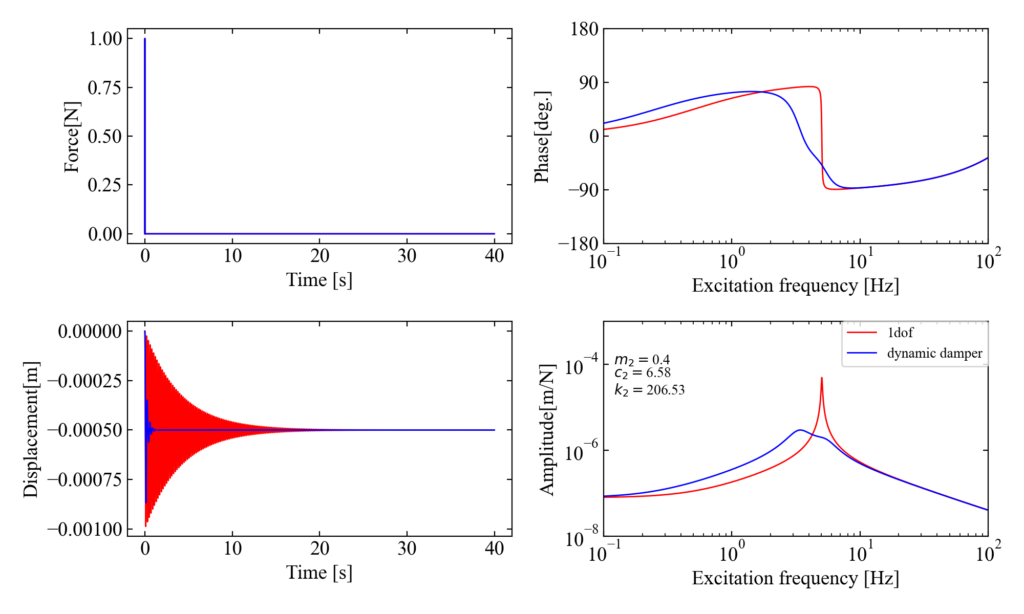
\(\mu=0.4, c_{1}=3\)
質量比\(\mu=0.4\)、減衰係数\(c_{1}=3\)として最適条件を計算したダイナミックダンパーの効果が以下です。
減衰後は\(c_{1}=1\)の時とほぼ変わっていませんね。
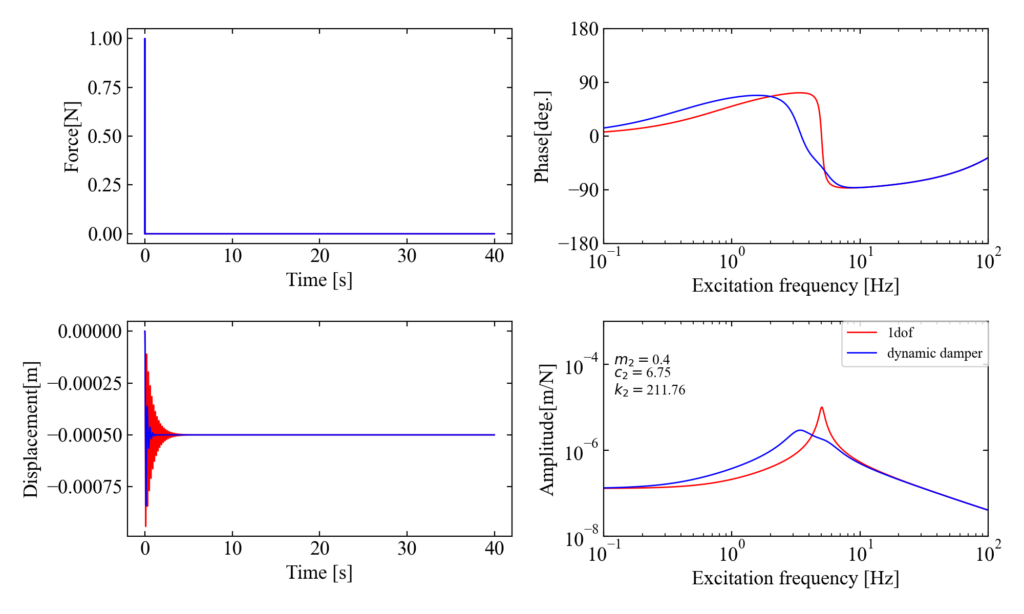
まとめ
本記事では前半に振動の問題について解説し、制振技術であるダイナミックダンパーを紹介しました。
ダイナミックダンパーには数多くのタイプがありますが、今回はパッシブ型かつ質量慣性利用型について説明しました。
Pythonで振動系のシミュレーションを行いながら、ダイナミックダンパーの振る舞いを観察しました。
素人考えでパラメータを調整しようとするとほぼ効果は出ませんでしたが(出たとしても、減衰比を思いっきり上げる等が必要=コスト大)、最適同調条件、最適減衰条件を考慮する事で劇的に制振する事が出来ました。
しかし、実際に設計を行う場合は「求めたパラメータをどう実製品に応用するか」が最も大変です。
ゴムを使う?減衰係数3.0[N s/m]ってどう作る??ちゃんと機能する???…といった感じ。ものづくりの難しい所です。
難しい所はありますが、基本の原理をしっかり把握して要件出しができるようになる事は重要です。僕も継続的に学習していこうと思います。
本日は振動工学の学習を行いました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
はじめまして。こちらのブログを参考にPythonによる振動系シミュレーションに取り組んでいるものです。まだPythonも振動工学についても知識が乏しいですが、wat様のブログのように丁寧に解説がなされている記事を確認しながら勉強に励んでいます。特にこのダイナミックダンパー×Pythonでの記述はこちらの記事が最も丁寧に書かれていると感じております。参考図書としてあげている動吸振器関連の書籍については現在入手困難となっておりまだ拝読できていないのですが、今後なんとしても入手できればと思っております。
要望にはなってしまうのですが、アクティブマスダンパ制御に関して今後ご解説いただくことはできないでしょうか?
ご訪問ありがとうございます。
ブログ記事を参考にして頂いてありがとうございます。
励みになります。
アクティブ系の制振についてはそのうちやりたいとは思っていますが、理論がまだ難しく、申し訳ないのですが、僕の力量ではまだ記事を書くレベルに至っていないのが正直なところです。
「動吸振器とその応用」をお読み頂くのと、制御系とPythonですと「Pythonによる制御工学入門」も参考になると思います。
アクティブ制振は実際に使えると非常に役に立つと思います。
このブログでもそのうち扱うと思いますが、時間がかかると思いますので、先行で着手して頂いた方が良いと考えます!