Pythonで基礎から学ぶ1次元梁モデルの有限要素法

有限要素法は一般的に商用ソフトやオープンソースのライブラリを活用して「使う」ことが多いものですが、理解するためには自分でプログラミングするのが一番です。ここでは手計算でもできるレベルの問題をPythonによる有限要素法コードで解くことで、計算の流れを把握することを目指します。

こんにちは。wat（@watlablog）です。ここではあえて簡単な問題をPythonによる有限要素法で解くことで基礎を学びます！

目次（項目クリックでジャンプできます）

この記事の目標と注意点

有限要素法の計算フローを学ぶ

有限要素法（FEM）とは？

有限要素法（FEM：Finite Element Method）は数値解析手法の一種で、解析的に解くことが難しい連続体を有限の小領域（要素）に分割して計算する手法です。
1956年ごろから導入されたとされており、研究が重ねられた現代では製品開発や構造検討には欠かせないツールとなっています。

基本の原理は簡単ですが、高速かつ高精度の計算を実現するためには数学的に高度なアルゴリズムが多数使われているのが事実です。そのため素人がチョット勉強して実用に耐える計算コードをつくるのは到底無理なことでしょう。

学習目的でどんなことをやっているかを知る

真面目に実用的なコードを書くのは専門のソフトウェア開発者に任せて、ここでは簡単な問題を有限要素法の手順に沿って解くことで、計算フローを学びます。どんなことをやっているか…を知ることを目標としているため、真面目にコードを書きたい方は回れ右です。

コードレベルで有限要素法を扱っているOSSのライブラリにGetFEM（https://getfem.readthedocs.io/ja/latest/）があります。以下の記事でも取り扱っていますが、本格的に勉強したい人はこれらのライブラリのソースコードやドキュメントを熟読することをおすすめします。
・WindowsのWSL2でPython3/GetFEMを使ってみた

正式な計算手順ではない（かもしれない）

上記のような理由のため、この記事に記載のコードはかなりラフに書いています。実際はもっと疎行列を適切に扱ったり数値計算アルゴリズムの工夫を行ったりすると思いますが、ここではそれらを無視して最低限の手順を追っただけという内容です。初心者が書いているので正確な手順でない可能性があることをご了承ください。

とはいえ筆者は以下の2冊を元に有限要素法のフローを勉強しています。詳細な式展開は書籍に任せますが、この2冊はPython本ではないですが、有限要素法の基礎を学ぶのに初心者にわかりやすく書いてあるのでおすすめします。

大学生が書いた有限要素法（FEM）のきょうか書

有限要素法を図解で解説した入門書です。土木に限らず様々な分野で活用されているにも関わらず、理論が複雑で理解しにくいものとなっています。大学生、高校生、高専生、学生時代に挫折したすべての人のために役立ちます。

Amazon

楽天

解析塾秘伝>有限要素法のつくり方! -FEMプログラミングの手順とノウハウ-

有限要素法(FEM)の基礎を習得した方を対象に10年間以上続いている、NPO法人CAE懇話会で行われている、FEMプログラムを作成する講義および実習「解析塾 FEMプログラミング」を1冊の本で紹介。FEMプログラミングの手順やノウハウを知ることで、自分でFEMプログラムを作ることを学ぶ本。

Amazon

楽天

動作環境

本記事のプログラムは以下のPython環境で動作確認を行いました。多分WindowsとMacの両方で動くと思います。

Python	Python 3.9.6
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.23.0
matplotlib	3.7.1

引張荷重が働く1次元3節点片持ち梁モデルの計算コード

問題定義

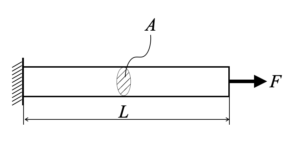
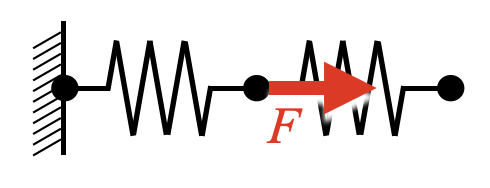
今回Pythonで計算する問題として、断面積\(A\)が一定、長さ\(L\)の梁モデルを長手方向に荷重\(F\)で引っ張るという状況を設定します（下図）。

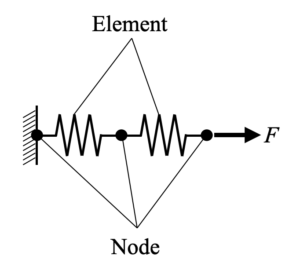
この梁を任意個数のばね要素で離散化すると最も簡単にFEMで計算できる力学モデルとなります（下図）。ここで、各ばねを繋ぐ点を節点（Node）とよび、ばね要素を単に要素（Element）と呼んでも良いです。下図は3節点2要素のモデルとなります。

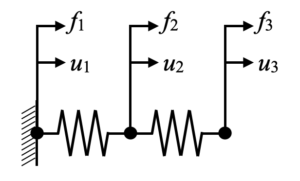
このモデルに荷重を与えて変位の計算を行います。数値計算をするためには変位や荷重の正負の方向を考える必要があります。変位を各節点で出力し、荷重も各節点で与えられるようにするには、下図のイメージを持っていれば問題ありません。上図のように右端に荷重を右方向に与える場合、\(f_{3}\)の正方向に荷重を設定し、\(f_{1}\)と\(f_{2}\)には0を設定するという意味になります。

ここで、梁は断面形状と材料が持つ物性で全体の強さが決まりますが、細かいことはプログラムの中で設定しながら解説していきましょう。

モデルの作成

まずは以下のコードでモデルを作成します。model関数ではまずnodes（節点）を定義し、節点の数によってelements（要素）が自動生成されるようにしてみました。今回は簡単なモデルが例ですが、この部分は複雑なモデルの場合ではメッシュ作成（メッシング、メッシュを切る…とも言う）の工程です。複雑な形状の場合は別途メッシングライブラリを使って節点や要素の情報を別ファイルで持つ方が便利でしょう。

def model():
    """ 1次元ばねモデル """

    # 節点と要素を定義
    nodes = np.array([0.0, 0.5, 1.0])
    elements = []
    for i in range(len(nodes) - 1):
        element = [nodes[i], nodes[i + 1]]
        elements.append(element)

    return nodes, elements

def model():

""" 1次元ばねモデル """

# 節点と要素を定義

nodes = np.array([0.0, 0.5, 1.0])

elements = []

for i in range(len(nodes) - 1):

element = [nodes[i], nodes[i + 1]]

elements.append(element)

return nodes, elements

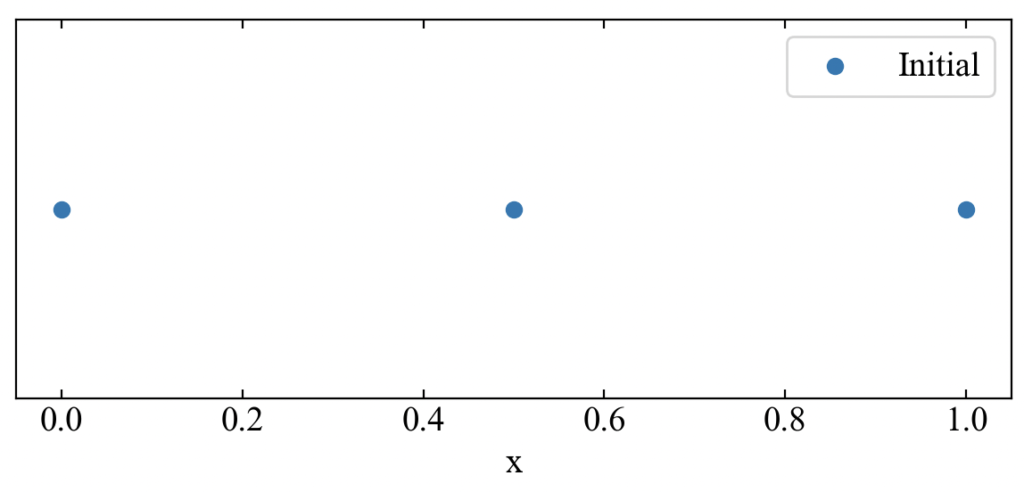
節点をmatplotlibで可視化するとこんな感じ。今回は全長\(L\)が1の3節点2要素モデルとしています。

Dマトリクスの作成

有限要素法では材質を表すDマトリクスと呼ばれる行列を作成します。詳しい説明は上記で紹介した書籍に委ねますが、通常3次元や2次元では材料が伸びるとその直交方向は細くなるという特性があり、これはポアソン比で表現します。今回のような1次元の問題ではその影響は無視できるため、以下のコードのようにDマトリクスはヤング率と等しくなります。

# 定数
E = 70e9
A = 3.14e-4

# Dマトリクス(1次元はヤング率と同じ）
D = E

# 定数

E = 70e9

A = 3.14e-4

# Dマトリクス(1次元はヤング率と同じ）

D = E

なぜ"D"なのか、というコラムは「解析塾秘伝有限要素法のつくり方!」に記載されています！

形状関数の作成

有限要素法では要素内における物理量の分布を表す関数として形状関数を用います。形状関数とは、ある節点の値が1で、それ以外の節点の値が0となる関数です。そして節点間の値を補間して繋ぐ役割を持ちます。1次元棒要素の場合は始点と終点の2点で1要素になりますが、式（1）で形状関数が与えられます。

\[ \begin{eqnarray} N_{1} &=& 1 - \frac{x}{L}\\ N_{2} &=& \frac{x}{L} \end{eqnarray} \tag{1} \]

全体のコードを最後に示しますが、3節点2要素の場合、形状関数は以下のアウトプットになります。2節点要素は1節点目が[1.0, 0.0], 2節点目が[0.0, 1.0]となっていることがわかります。このような処理を有限要素法計算の中に取り入れることで、グローバル座標系で複雑な変形をしても、要素内で正規化された座標系で物理量の計算ができるようになります。

Shape functions= [[array([1., 0.]), array([0., 1.])], [array([1., 0.]), array([0., 1.])]]

1	Shape functions= [[array([1., 0.]), array([0., 1.])], [array([1., 0.]), array([0., 1.])]]

Bマトリクスの作成

Bマトリクスとは形状関数の微分形式を成分に持つマトリクスです。Dマトリクスが材料の物性から応力とひずみを結びつけるものとすると、Bマトリクスは変位とひずみを結びつける作用があります。今回の1次元棒要素のBマトリクスは式（1）を微分した式（2）で与えられます。

\[ \begin{eqnarray} \frac{dN_{1}}{dx} &=& - \frac{1}{L}\\ \frac{dN_{2}}{dx} &=& \frac{1}{L} \end{eqnarray} \tag{2} \]

B_matrix関数を以下のように作ってみました。ここはSympyを使ったりすると自動で微分を考慮できるかも知れませんね。

def B_matrix(element):
    """ 2節点棒要素のBマトリクス（形状関数の微分） """

    L = element[1] - element[0]
    b = np.array([-1 / L, 1 / L])

    return b

def B_matrix(element):

""" 2節点棒要素のBマトリクス（形状関数の微分） """

L = element[1] - element[0]

b = np.array([-1 / L, 1 / L])

return b

要素剛性マトリクスの作成

Bマトリクスが得られたら、要素剛性マトリクス\(K_{e}\)を作成します。1次元棒要素の要素剛性マトリクスの定義式は式（3）です。

\[ [K_{e}] = A\int_{0}^{L} [B]^{\mathrm{T}}[D][B] dx \tag{3} \]

複雑な要素の場合はガウス積分等を使いますが、ここでは最も簡単な1次元2節点の要素を扱っているため、以下の特性を使って式（4）と簡略化します。

1次元2節点要素におけるBマトリクスの成分は要素の長さLにのみ依存する。
Bマトリクスは要素全体で一定の値となる。
関数が一定の値をとるという特性を利用すると、その一定値と区間長さの積となる。

\[ [K_{e}] = A L [B]^{\mathrm{T}}[D][B] \tag{4} \]

形状関数、Bマトリクスを作りながら要素剛性マトリクスを作成するコードを以下に示します。

def elements_stiffness_matrix(elements, D, A):
    """ 要素剛性マトリクスを作る関数 """

    # 2節点棒要素の形状関数
    N = []
    for i in range(len(elements)):
        # 起点を0にする
        element_normalized = elements[i] - elements[i][0]

        # 要素毎の形状関数のappend
        N.append(shape_function_beam(element_normalized, element_normalized[1]))
    print('Shape functions=', N)

    # 2節点棒要素のBマトリクス
    B = []
    for i in range(len(elements)):
        print(elements[i])
        B.append(B_matrix(elements[i]))
    print('B matrix=', B)

    # 要素剛性マトリクス
    Ke_list = []
    for i in range(len(elements)):
        L = elements[i][1] - elements[i][0]
        Ke = A * np.outer(B[i].T, B[i] * D) * L
        Ke_list.append(Ke)
    print('Ke=', Ke_list)

    return Ke_list

def elements_stiffness_matrix(elements, D, A):

""" 要素剛性マトリクスを作る関数 """

# 2節点棒要素の形状関数

N = []

for i in range(len(elements)):

# 起点を0にする

element_normalized = elements[i] - elements[i][0]

# 要素毎の形状関数のappend

N.append(shape_function_beam(element_normalized, element_normalized[1]))

print('Shape functions=', N)

# 2節点棒要素のBマトリクス

B = []

for i in range(len(elements)):

print(elements[i])

B.append(B_matrix(elements[i]))

print('B matrix=', B)

# 要素剛性マトリクス

Ke_list = []

for i in range(len(elements)):

L = elements[i][1] - elements[i][0]

Ke = A * np.outer(B[i].T, B[i] * D) * L

Ke_list.append(Ke)

print('Ke=', Ke_list)

return Ke_list

全体剛性マトリクスの作成

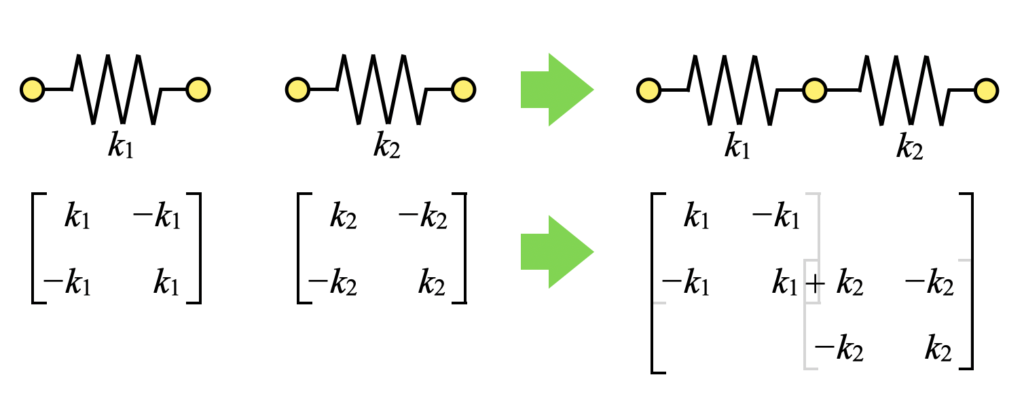
要素剛性マトリクスを対応する節点位置で重ね合わせることで全体剛性マトリクスができあがります。剛性マトリクスの重ね合わせは過去に以下の記事で扱いました。詳細は記事を確認していただければと思いますが、概念図もこのページに記載しておきます。
・csvの値から直列ばねマスモデルを自動生成するPythonコード

拘束条件の設定

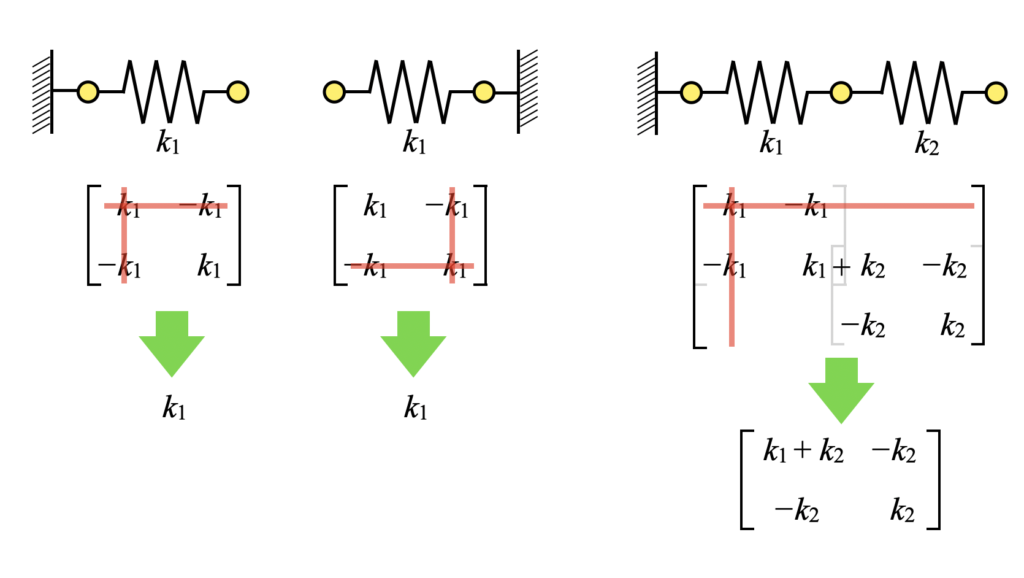
全体剛性マトリクスが組み上がったら拘束条件の設定を行います。ここでは拘束条件は完全拘束を設定しますが、これは全体剛性マトリクスの対応節点部分の行列を削除することで表現します（0＝0で連立方程式からその行の方程式が削除されるという意味）。

1次元2節点棒要素の全体剛性マトリクスを作成する関数を以下に示します。

def global_stiffness_matrix(Ke_list, nodes):
    """ 全体剛性行列の作成 """

    # 要素行列の重ね合わせ
    K = np.zeros((len(nodes), len(nodes)))
    for i in range(len(Ke_list)):
        K[i:i+2, i:i+2] += Ke_list[i]

    # 第1行、第1列を削除（左端節点の完全拘束）
    K = np.delete(K, 0, axis=0)
    K = np.delete(K, 0, axis=1)

    return K

def global_stiffness_matrix(Ke_list, nodes):

""" 全体剛性行列の作成 """

# 要素行列の重ね合わせ

K = np.zeros((len(nodes), len(nodes)))

for i in range(len(Ke_list)):

K[i:i+2, i:i+2] += Ke_list[i]

# 第1行、第1列を削除（左端節点の完全拘束）

K = np.delete(K, 0, axis=0)

K = np.delete(K, 0, axis=1)

return K

剛性方程式の解法（ソルバー）

ここまで完成すれば後は方程式を解くだけです。解くべき式は全体剛性マトリクス\([K]\)と変位ベクトル\(\{u\}\)、荷重ベクトル\(\{F\}\)で構成される剛性方程式（5）です。

\[ \{F\} = [K]\{u\} \tag{5} \]

これを変位ベクトル\(\{u\}\)について解く場合は式（6）となります。

\[ \{u\} = [K]^{-1}\{F\} \tag{6} \]

プログラム的に連立方程式を解く方法は、当ブログでも扱ったヤコビ法、ガウス・ザイデル法、SOR法等の反復法がありますが、ここではせっかくPythonを使うのでnumpyのsolveを使ってみます（多分こっちの方が高速）。

def solve(K, F):
    """ ソルバー """

    U = np.linalg.solve(K, F)

    return U

def solve(K, F):

""" ソルバー """

U = np.linalg.solve(K, F)

return U

結果の可視化を含む全コード

ここでは以下の条件で計算をしています。
半径10mmのアルミの長い棒をイメージしています。荷重はこんなにかけたら壊れると思いますが、グラフにプロットした時に伸びがわかりやすくなるよう大げさにしています。

ヤング率\(E\)=70[GPa]
半径\(r\)=10[mm]=0.01[m]
長さ\(L\)=1.0[m]（model関数内のnodesで定義）
荷重\(F\)=1000[kN]

注意点として、有限要素法の計算では一般的に単位系はユーザーで整合性がとれるように設定します。入力する数値の単位には気をつけましょう。

例えば某衝突計算が得意な商用ソフトでは「N-s-mm-ton」がよく使われますが、そこで計算された応力は「N/mm\(^{2}\)」になるので「MPa」になります。

以下に結果のプロットを含む全体のコードを示します。

import numpy as np
from matplotlib import pyplot as plt

def model():
    """ 1次元ばねモデル """

    # 節点と要素を定義
    nodes = np.array([0.0, 0.5, 1.0])
    elements = []
    for i in range(len(nodes) - 1):
        element = [nodes[i], nodes[i + 1]]
        elements.append(element)

    return nodes, elements


def shape_function_beam(x, L):
    """ 2節点棒要素の形状関数 """

    N1 = 1 - x/L
    N2 = x/L

    return [N1, N2]

def B_matrix(element):
    """ 2節点棒要素のBマトリクス（形状関数の微分） """

    L = element[1] - element[0]
    b = np.array([-1 / L, 1 / L])

    return b


def elements_stiffness_matrix(elements, D, A):
    """ 要素剛性マトリクスを作る関数 """

    # 2節点棒要素の形状関数
    N = []
    for i in range(len(elements)):
        # 起点を0にする
        element_normalized = elements[i] - elements[i][0]

        # 要素毎の形状関数のappend
        N.append(shape_function_beam(element_normalized, element_normalized[1]))
    print('Shape functions=', N)

    # 2節点棒要素のBマトリクス
    B = []
    for i in range(len(elements)):
        print(elements[i])
        B.append(B_matrix(elements[i]))
    print('B matrix=', B)

    # 要素剛性マトリクス
    Ke_list = []
    for i in range(len(elements)):
        L = elements[i][1] - elements[i][0]
        Ke = A * np.outer(B[i].T, B[i] * D) * L
        Ke_list.append(Ke)
    print('Ke=', Ke_list)

    return Ke_list


def global_stiffness_matrix(Ke_list, nodes):
    """ 全体剛性行列の作成 """

    # 要素行列の重ね合わせ
    K = np.zeros((len(nodes), len(nodes)))
    for i in range(len(Ke_list)):
        K[i:i+2, i:i+2] += Ke_list[i]

    # 第1行、第1列を削除（左端節点の完全拘束）
    K = np.delete(K, 0, axis=0)
    K = np.delete(K, 0, axis=1)

    return K

def solve(K, F):
    """ ソルバー """

    U = np.linalg.solve(K, F)

    return U


def plot(U0, U):
    """ グラフ描画する関数 """

    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure(figsize=(6, 3))
    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')

    # 軸のラベルを設定する。
    ax1.set_xlabel('x')
    ax1.set_ylabel('y')

    # データをプロットする。
    ax1.scatter(U0, np.zeros_like(U0), label='Initial')
    ax1.scatter(U0 + U, np.zeros_like(U), label='Deform')
    ax1.legend()
    ax1.tick_params(labelleft=False, labelright=False)
    ax1.tick_params(left=False, right=False)

    # グラフを表示する。
    fig.tight_layout()
    plt.show()
    plt.close()

    return


if __name__ == '__main__':
    """ Main """

    # モデル
    nodes, elements = model()
    print('Nodes=', nodes)
    print('Elements=', elements)

    # 定数（ヤング率E=70GPa, 半径r=0.01[m]）
    E = 70e9
    A = 3.14e-4

    # Dマトリクス(1次元はヤング率と同じ）
    D = E

    # 要素剛性マトリクス
    Ke = elements_stiffness_matrix(elements, D, A)

    # 全体剛性マトリクス
    K = global_stiffness_matrix(Ke, nodes)
    print('K_global =\n', K)

    # 荷重ベクトル
    F = np.zeros(len(nodes) - 1)
    F[-1] = 1000000.0
    print('F=', F)

    # 解析実行（ソルバー）
    U = solve(K, F)
    U = np.insert(U, 0, 0)
    print('U=', U)

    # 結果の可視化
    plot(nodes, U

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

import numpy as np

from matplotlib import pyplot as plt

def model():

""" 1次元ばねモデル """

# 節点と要素を定義

nodes = np.array([0.0, 0.5, 1.0])

elements = []

for i in range(len(nodes) - 1):

element = [nodes[i], nodes[i + 1]]

elements.append(element)

return nodes, elements

def shape_function_beam(x, L):

""" 2節点棒要素の形状関数 """

N1 = 1 - x/L

N2 = x/L

return [N1, N2]

def B_matrix(element):

""" 2節点棒要素のBマトリクス（形状関数の微分） """

L = element[1] - element[0]

b = np.array([-1 / L, 1 / L])

return b

def elements_stiffness_matrix(elements, D, A):

""" 要素剛性マトリクスを作る関数 """

# 2節点棒要素の形状関数

N = []

for i in range(len(elements)):

# 起点を0にする

element_normalized = elements[i] - elements[i][0]

# 要素毎の形状関数のappend

N.append(shape_function_beam(element_normalized, element_normalized[1]))

print('Shape functions=', N)

# 2節点棒要素のBマトリクス

B = []

for i in range(len(elements)):

print(elements[i])

B.append(B_matrix(elements[i]))

print('B matrix=', B)

# 要素剛性マトリクス

Ke_list = []

for i in range(len(elements)):

L = elements[i][1] - elements[i][0]

Ke = A * np.outer(B[i].T, B[i] * D) * L

Ke_list.append(Ke)

print('Ke=', Ke_list)

return Ke_list

def global_stiffness_matrix(Ke_list, nodes):

""" 全体剛性行列の作成 """

# 要素行列の重ね合わせ

K = np.zeros((len(nodes), len(nodes)))

for i in range(len(Ke_list)):

K[i:i+2, i:i+2] += Ke_list[i]

# 第1行、第1列を削除（左端節点の完全拘束）

K = np.delete(K, 0, axis=0)

K = np.delete(K, 0, axis=1)

return K

def solve(K, F):

""" ソルバー """

U = np.linalg.solve(K, F)

return U

def plot(U0, U):

""" グラフ描画する関数 """

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure(figsize=(6, 3))

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('x')

ax1.set_ylabel('y')

# データをプロットする。

ax1.scatter(U0, np.zeros_like(U0), label='Initial')

ax1.scatter(U0 + U, np.zeros_like(U), label='Deform')

ax1.legend()

ax1.tick_params(labelleft=False, labelright=False)

ax1.tick_params(left=False, right=False)

# グラフを表示する。

fig.tight_layout()

plt.show()

plt.close()

return

if __name__ == '__main__':

""" Main """

# モデル

nodes, elements = model()

print('Nodes=', nodes)

print('Elements=', elements)

# 定数（ヤング率E=70GPa, 半径r=0.01[m]）

E = 70e9

A = 3.14e-4

# Dマトリクス(1次元はヤング率と同じ）

D = E

# 要素剛性マトリクス

Ke = elements_stiffness_matrix(elements, D, A)

# 全体剛性マトリクス

K = global_stiffness_matrix(Ke, nodes)

print('K_global =\n', K)

# 荷重ベクトル

F = np.zeros(len(nodes) - 1)

F[-1] = 1000000.0

print('F=', F)

# 解析実行（ソルバー）

U = solve(K, F)

U = np.insert(U, 0, 0)

print('U=', U)

# 結果の可視化

plot(nodes, U

このコードを実行すると、以下のプロットが表示されます。Initialの点が初期の節点座標、Deformは変位を反映させた節点座標です。意図した通り左端は固定され、右端が伸びている結果を得ることができました。

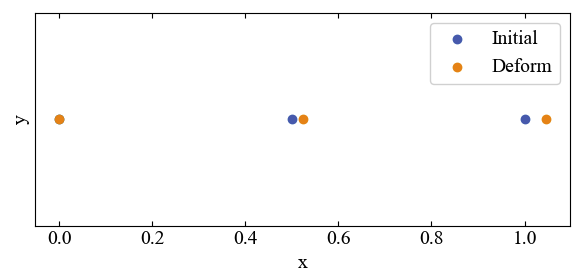
出力ウィンドウには色々出てきていると思いますが、変位ベクトル\(U\)の値は以下のようになりました。これは各節点の変位を意味しています。

U= [0.         0.02274795 0.04549591]

1	U= [0. 0.02274795 0.04549591]

0.0455[m]…アルミ棒が45[mm]も伸びました（破断必至）。
さて、これが本当に正しいのか…検証してみましょう！

結果の検証

新しく計算コードを作った時や人のコードを使う時は、理論的にわかっているモデルで結果の検証をすると設定やコードの間違いに気付くため有用です。是非仕事でFEMを使っている人も簡単な問題で理論値と比較してみましょう。

今回は棒材の伸びという材料力学の中でも最も簡単な問題です。以下の手順で荷重に対する変位を求めることができます。

応力は荷重\(F\)と断面積\(A\)を使って式（7）の関係を持ち、さらにヤング率\(E\)とひずみ\(\epsilon\)の間には式（8）の関係があります。

\[ \sigma = \frac{F}{A} \tag{7} \]

\[ \sigma = E \epsilon \tag{8} \]

ひずみ\(\epsilon\)は伸び\(\delta\)と長さ\(L\)の間に式（9）の関係が成り立つため、これら3つの関係式を整理すると式（10）を得ます。

\[ \epsilon = \frac{\delta}{L} \tag{9} \]

\[ \delta = \frac{LF}{EA} \tag{10} \]

式（10）に値を代入して伸び\(\delta\)を計算すると以下の結果を得ます。

\[ \begin{eqnarray} \delta = \frac{LF}{EA}　&=& \frac{1.0 \times 1e6}{70e9 \times 3.14e-4}\\ &=& 0.0455... \end{eqnarray} \]

先ほど自分で書いたコードの計算結果とばっちり一致しましたね！

モデルを変更して動作確認をする

節点数（要素数）を増やしてみる

model関数のnodesをnp.linspace()で10節点にしてみましょう。

def model():
    """ 1次元ばねモデル """

    # 節点と要素を定義
    #nodes = np.array([0.0, 0.5, 1.0])
    nodes = np.linspace(0.0, 1, 10)
    elements = []
    for i in range(len(nodes) - 1):
        element = [nodes[i], nodes[i + 1]]
        elements.append(element)

    return nodes, elements

def model():

""" 1次元ばねモデル """

# 節点と要素を定義

#nodes = np.array([0.0, 0.5, 1.0])

nodes = np.linspace(0.0, 1, 10)

elements = []

for i in range(len(nodes) - 1):

element = [nodes[i], nodes[i + 1]]

elements.append(element)

return nodes, elements

実行結果がこちら。

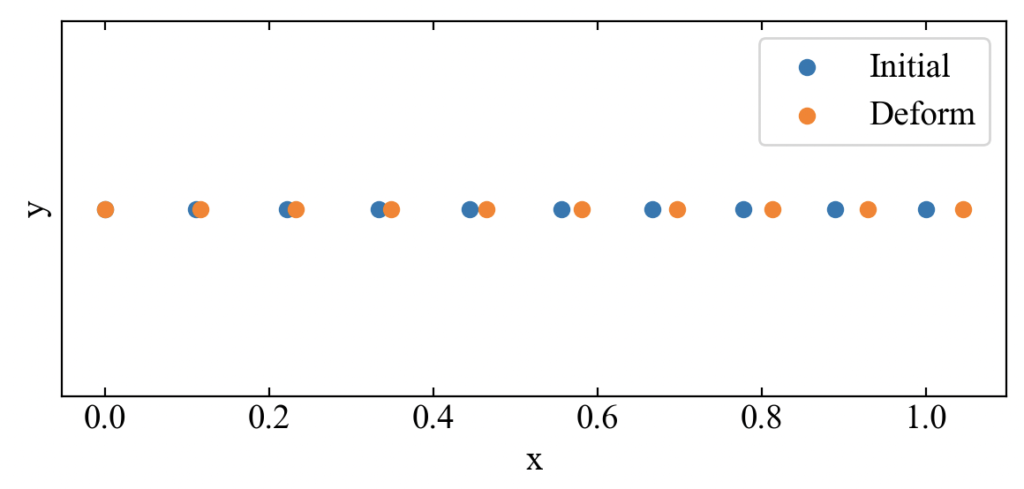
全長が変わることなく分割数が増えただけなので、右端の節点変位は先ほどと変わらず理論値と一致しています。

U= [0.         0.0050551  0.0101102  0.0151653  0.0202204  0.0252755
 0.0303306  0.0353857  0.0404408  0.04549591]

1 2	U= [0. 0.0050551 0.0101102 0.0151653 0.0202204 0.0252755 0.0303306 0.0353857 0.0404408 0.04549591]

全長を変更してみる

棒の長さ\(L\)を2倍にしてみましょう。

def model():
    """ 1次元ばねモデル """

    # 節点と要素を定義
    nodes = np.array([0.0, 1.0, 2.0])
    #nodes = np.linspace(0.0, 1, 10)
    elements = []
    for i in range(len(nodes) - 1):
        element = [nodes[i], nodes[i + 1]]
        elements.append(element)

    return nodes, elements

def model():

""" 1次元ばねモデル """

# 節点と要素を定義

nodes = np.array([0.0, 1.0, 2.0])

#nodes = np.linspace(0.0, 1, 10)

elements = []

for i in range(len(nodes) - 1):

element = [nodes[i], nodes[i + 1]]

elements.append(element)

return nodes, elements

2.0[m]のアルミ棒に1.0MNかけることは滅多に無いことかも知れませんが、結果はこちら。

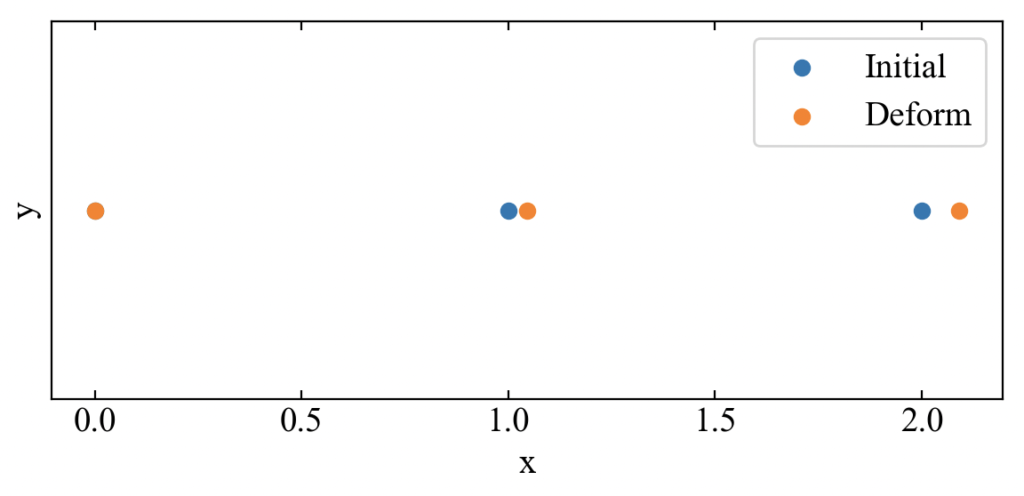
変位結果はこちら。式（10）のLに2を代入すると0.0909[m]と計算されるので、これも理論値と同じですね！

U= [0.         0.04549591 0.09099181]

1	U= [0. 0.04549591 0.09099181]

途中の節点に荷重をかけてみる

次は2.0[m]のアルミ棒に対して、1.0[m]の位置に引張荷重をかけてみます。理屈的には\(L\)=1.0[m]の棒を引っ張った時と同じ伸び量になるはずです。

コードは以下の部分を変更しました。F[-2]とすることで最後から2番目の節点に荷重をかけられます。

def model():
    """ 1次元ばねモデル """

    # 節点と要素を定義
    nodes = np.array([0.0, 1.0, 2.0])
    #nodes = np.linspace(0.0, 1, 10)
    elements = []
    for i in range(len(nodes) - 1):
        element = [nodes[i], nodes[i + 1]]
        elements.append(element)

    return nodes, elements

# 荷重ベクトル
F = np.zeros(len(nodes) - 1)
F[-2] = 1000000.0
print('F=', F)

def model():

""" 1次元ばねモデル """

# 節点と要素を定義

nodes = np.array([0.0, 1.0, 2.0])

#nodes = np.linspace(0.0, 1, 10)

elements = []

for i in range(len(nodes) - 1):

element = [nodes[i], nodes[i + 1]]

elements.append(element)

return nodes, elements

# 荷重ベクトル

F = np.zeros(len(nodes) - 1)

F[-2] = 1000000.0

print('F=', F)

節点変位図がこちら。2番目と3番目の節点変位が同程度になっています。

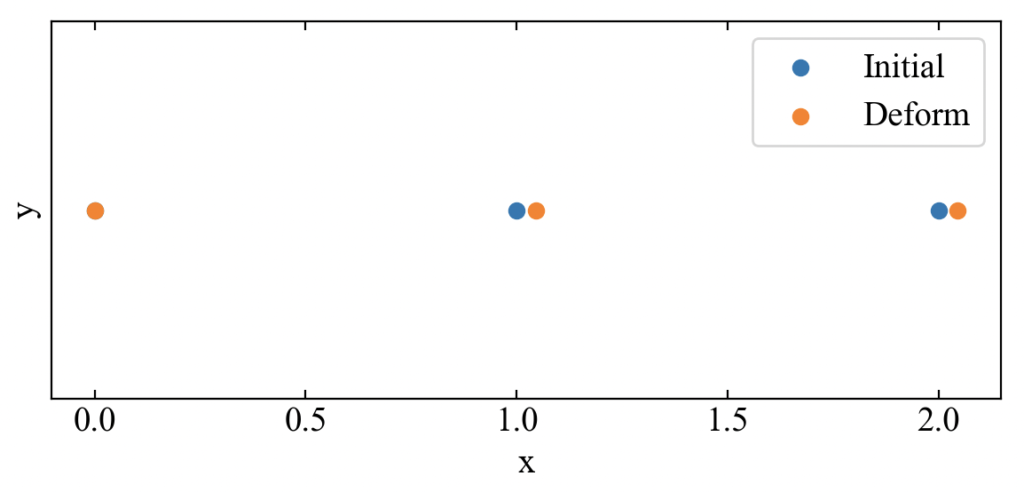
本当に同程度なのかUの値を確認してみると、確かに2番目と3番目の節点は全く同じ変位量でした。そして1.0[m]の棒を伸ばした時と同じ値になっているので理論値とも一致していますね。

U= [0.         0.04549591 0.04549591]

1	U= [0. 0.04549591 0.04549591]

荷重ベクトルの作り方について

今回、荷重ベクトルは全体剛性マトリクスに対応するように最後に作成しましたが、正しくは要素剛性マトリクスを作る時に一緒に作るのがよかったのかも知れません。

標準問題集の第4章26問目とその解説\(^{[2]}\)を読むと「荷重ベクトル（等価節点力ベクトル）は, 要素における値を重ね合わせてばね系全体の荷重ベクトルとするため…」の文があります。汎用のFEMコードではそうなっているのでしょうか。一応念頭に置いておきましょう。

まとめ

この記事では有限要素法（FEM）の基礎を学ぶためにPythonでゼロから解析コードを書いてみました。
まだバグがあるかも知れませんが、まずは1次元の棒要素に引張荷重をかける解析は理論値と一致することを確認しました。

とはいえ、定式化の部分は2節点棒要素ならではの簡略化が入っていることから、汎用的に使うにはまだまだ改良が必要でしょう。

しかし自分でコードを書いてみると形状関数の意味や計算の手順をほんの少し理解することができました。計算力学技術者試験の勉強としては良い経験になったと思います。
余裕があれば違う固体力学の問題も解いていきたいと思います。プログラミングばかりしていると楽しいですが試験には落ちそうなのでほどほどに…（固体2級の合格率は30％前後らしい？？）。

参考文献

[1]:Clough, R. W., Martin, H. C., Topp, L. J., & Turner, M. J. (1956). Stiffness and deflection analysis of complex structures. Journal of the Aeronautical Sciences, 23(9).

[2]:標準問題集計算力学技術者2級（固体力学分野の有限要素法解析技術者）, 日本機械学会, 第10版, (2020), pp53 pp207

FEMのコーディングに入門しました！
Xでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

Pythonで基礎から学ぶ1次元梁モデルの有限要素法

この記事の目標と注意点

有限要素法の計算フローを学ぶ

有限要素法（FEM）とは？

学習目的でどんなことをやっているかを知る

正式な計算手順ではない（かもしれない）

動作環境

引張荷重が働く1次元3節点片持ち梁モデルの計算コード

問題定義

モデルの作成

Dマトリクスの作成

形状関数の作成

Bマトリクスの作成

要素剛性マトリクスの作成

全体剛性マトリクスの作成

拘束条件の設定

剛性方程式の解法（ソルバー）

結果の可視化を含む全コード

結果の検証

モデルを変更して動作確認をする

節点数（要素数）を増やしてみる

全長を変更してみる

途中の節点に荷重をかけてみる

荷重ベクトルの作り方について

まとめ

参考文献

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

この記事の目標と注意点

有限要素法の計算フローを学ぶ

有限要素法（FEM）とは？

学習目的でどんなことをやっているかを知る

正式な計算手順ではない（かもしれない）

動作環境

引張荷重が働く1次元3節点片持ち梁モデルの計算コード

問題定義

モデルの作成

Dマトリクスの作成

形状関数の作成

Bマトリクスの作成

要素剛性マトリクスの作成

全体剛性マトリクスの作成

拘束条件の設定

剛性方程式の解法（ソルバー）

結果の可視化を含む全コード

結果の検証

モデルを変更して動作確認をする

節点数（要素数）を増やしてみる

全長を変更してみる

途中の節点に荷重をかけてみる

荷重ベクトルの作り方について

まとめ

参考文献

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル