Pythonで連立方程式をヤコビ法（反復法）で解く方法

連立方程式の解法は直接法がわかりやすいですが、巨大な方程式の場合は計算時間が問題となります。ここでは直接法に比べ高速に連立方程式を解くことができる反復法の中で、比較的ポピュラーなヤコビ法を注意点と共に説明しPythonで実装してみます。

こんにちは。wat(@watlablog)です。
ここでは反復法による連立方程式の解法として、ヤコビ法をPython実装と共に紹介します！

目次（項目クリックでジャンプできます）

反復法とヤコビ法の概要

直接法と反復法

連立方程式は中学校で習いますが、連立方程式を解く手法が数多くあることは大学に入るまで触れないかも知れません。

当WATLABブログでは「Numpyだけで書いたガウスの消去法で連立1次方程式を解いてみた」でガウスの消去法を学びました。

ガウスの消去法は前進消去と後退代入という行基本操作を有限回数行うことで機械的に連立方程式を解く方法でした。プログラミングで実装するためにはピボット選択が必要でしたが、人が解く場合は中学校で習う方法と同じです。

この方法で導いた方程式の解は計算過程に誤差が含まれない限り厳密であり、このような方法を直接法（Direct Method）と呼びます。

反復法（Iterative Method）とは、有限な計算プロセスでは厳密な解が得られない代わりに、計算に使うメモリを大きく削減したり少ない計算で良い結果が得られる手法です。

反復法の使い所

反復法は厳密解を得る保証がどこにもない手法ですが、大規模な連立方程式を解く必要がある場合に威力を発揮します。

連立方程式は行列形式で計算可能なことは明らかですが、有限要素法の剛性行列や数値流体力学で現れる楕円型偏微分方程式を解く時にできるような大規模な行列は時に数億行といった大きなサイズになります。

このような行列を有する連立方程式を直接法で解こうとすると、現代のコンピュータをもってしてもメモリ不足や計算時間がかかりすぎるという問題に直面します。

反復法はこれら大規模連立方程式を現実的な時間で近似したり、並列計算ができたりといったメリットが期待される時に使用します。

反復法の注意点：収束性

反復法も万能ではありません。今回のヤコビ法を含む反復法の多くは優対角行列（Diagonally dominant matrix）でないと収束しにくいという注意点があります。

優対角行列かどうかは式（1）で定義されます。この式は対角成分の絶対値が、その他残り要素の絶対値の和に等しいか、それよりも大きいかどうかを調べる目的で使います。

\[ |a_{ii}| \geq \left ( \sum^{i-1}_{j=1} + \sum^{n}_{j=i+1} |a_{ij}| \right ) \tag{1} \]

幸い先ほど紹介した大規模な行列は対角成分にほとんどの成分が集まる疎行列（Sparse matrix）になりやすいためこの優対角行列の判定はそれほど問題になりません。

しかし、コードを書いて使う時に「収束しない理由」を知っておくことは重要でしょう。

ヤコビ法の漸化式

ここで扱う連立方程式は式（2）で表す形式を対象とします。

ここで\(\mathbf{A}\)は係数行列、\(\mathbf{x}\)は解ベクトル、\(\mathbf{b}\)は定数ベクトルです（行列やベクトルなので斜体ではない太字で書いています）。

この記法に慣れていない方は「Pythonで線形代数！連立1次方程式を解く」に基礎的な内容を書いていますので、是非記事を確認してみてください。

\[ \mathbf{A}\mathbf{x}=\mathbf{b} \tag{2} \]

ここで\(\mathbf{A}=(\mathbf{D}+\mathbf{R})\)と置くと、式（2）は式（3）となります（\(\mathbf{D}\)は対角行列、\(\mathbf{R}\)は残りを意味する剰余行列）。

\[ (\mathbf{D}+\mathbf{R})\mathbf{x}=\mathbf{b} \tag{3} \]

式（3）を変形していくと式（4）の形になり、右辺の解ベクトルを\(n\)ステップ目、左辺の解ベクトルを\(n+1\)回目の解とすると式（5）の漸化式の形にできます。これがヤコビ法（Jacobi Method）の式となります。

\[ \begin{eqnarray} (\mathbf{D}+\mathbf{R})\mathbf{x}&=&\mathbf{b}\\ \mathbf{D}\mathbf{x}+\mathbf{R}\mathbf{x}&=&\mathbf{b}\\ \mathbf{D}\mathbf{x}&=&\mathbf{b}-\mathbf{R}\mathbf{x}\\ \mathbf{x}&=&\mathbf{D}^{-1}(\mathbf{b}-\mathbf{R}\mathbf{x})\tag{4} \end{eqnarray} \]

\[ \mathbf{x}_{n+1}=\mathbf{D}^{-1}(\mathbf{b}-\mathbf{R}\mathbf{x}_{n}) \tag{5} \]

式（5）は対角行列\(\mathbf{D}\)が逆行列形式で書いてありますが、対角行列の逆行列は単純に逆数にすれば良いため、逆行列の計算失敗等を懸念する必要はありません。

この計算を繰り返して収束判定を入れることで反復法が成立します。

なぜ係数行列を対角行列と剰余行列に分けるのか、なぜ\(x_{n+1}\)と\(x_{n}\)に分けることができるのかは、以下の連立方程式の変形と係数行列の関係に理由があります。

なぜ対角行列と剰余行列に分けるのか？

式（5）は対角行列と剰余行列を使っていますが、なぜこのような行列を使うのかは、やはり次の行列形式でない連立方程式を書いてみるのがわかりやすいと思います。

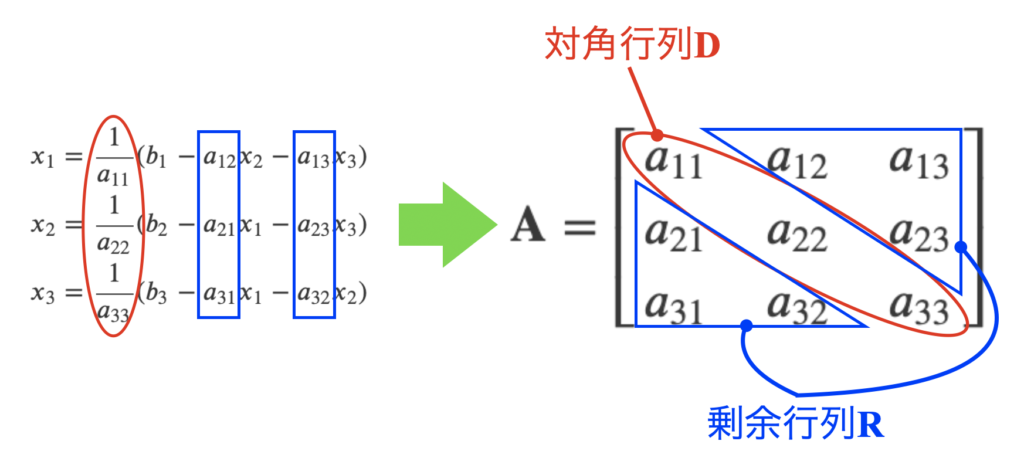
式（6）に3元連立方程式を示します。

\[ \begin{eqnarray} a_{11}x_{1} + a_{12}x_{2} + a_{13}x_{3} = b_{1}\\ a_{21}x_{1} + a_{22}x_{2} + a_{23}x_{3} = b_{2}\\ a_{31}x_{1} + a_{32}x_{2} + a_{33}x_{3} = b_{3} \end{eqnarray} \tag{6} \]

この式を式（7）と変形することで、それぞれ解を求める式になります。

\[ \begin{eqnarray} x_{1} &=& \frac{1}{a_{11}} (b_{1} - a_{12}x_{2} - a_{13}x_{3}) \\ x_{2} &=& \frac{1}{a_{22}} (b_{2} - a_{21}x_{1} - a_{23}x_{3}) \\ x_{3} &=& \frac{1}{a_{33}} (b_{3} - a_{31}x_{1} - a_{32}x_{2}) \end{eqnarray} \tag{7} \]

ここで、右辺は最初に係数\(a_{ii}\)と対角成分の逆数がかかっていることがわかると思います。

また、右辺\(x\)は左辺以外の\(x\)です（\(x_{1}\)を求めるためには、それ以外（剰余）の\(x_{2}, x_{3}\)を使う）。

係数に着目して図解すると下図になります。このように、式（5）の意味は連立方程式を変形した後の係数行列の関係から導かれているとわかりました。

収束判定

収束判定は今回式（8）で行います。この式の左辺は残差（Residual）と呼ばれることもあります。

このResidualが指定したトレランス以下になった時に計算を打ち切るようにプログラミングします。

\[ \frac{||\mathbf{x}_{n+1}-\mathbf{x}_{n}||}{||\mathbf{x}_{n+1}||} \leq tolerance \tag{8} \]

連立方程式をヤコビ法で反復的に解くPythonコード

動作環境

このページでは以下の環境で動作確認を行ったコードを掲載しています。

Python環境

Python	Python 3.9.6
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.21.1

PC環境

Mac	OS	macOS Catalina 10.15.7
	CPU	1.4[GHz]
	メモリ	8[GB]

サンプルコード

以下にサンプルコードを示します。コードの最後には答え合わせとしてnumpy.linalg.solveで求めた解を比較しています。そして、求めた係数行列と解ベクトルとの内積を計算して定数ベクトルとなるかどうかで検算もしています。

※Numpyの公式ページからnumpy.linalg.solveのソースコードを見ると、コレスキー分解とか下三角といった計算がされているのでこちらはLU分解法で計算しているものと考えられます（よく読んでないけど）。

import numpy as np

def jacobi(A, b, tolerance):
    ''' 連立方程式をヤコビ法（反復法）で解く '''

    # 初期化（適当な解と残差）
    x0 = np.random.random(len(b))
    residual = 1e20

    # A = D + R
    D = np.diag(A)
    R = A - np.diag(D)

    # 反復計算=>残差がトレランスより小さくなったら終了
    i = 0
    print('----------Start iteration----------')
    while residual > tolerance:
        # 解と残差を計算
        x = (b - (R @ x0)) / D
        residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2))

        if i % 100 == 0:
            print('Iteration=', i)
            print('Residual=', residual)
            print('x=', x)
        i += 1
        x0 = x

    print('----------End iteration----------')
    print('Iteration=', i)
    print('Residual=', residual)
    print('x=', x, '\n')

    return x

if __name__ == '__main__':
    # 係数行列と定数ベクトル
    A = np.array([[2, 1, 1],
                  [2, 3, 1],
                  [1, 1, 3]])
    b = np.array([2, 4, -1])

    # ヤコビ法で解を反復計算
    x_jacobi = jacobi(A, b, 1e-6)
    print('Jacobi method x=', x_jacobi, 'Validated b=', A @ x_jacobi)

    # numpyの線形代数ライブラリで検証
    x_linalg = np.linalg.solve(A, b)
    print('np.linalg.solve x=', x_linalg, 'Validated b=', A @ x_linalg)

import numpy as np

def jacobi(A, b, tolerance):

''' 連立方程式をヤコビ法（反復法）で解く '''

# 初期化（適当な解と残差）

x0 = np.random.random(len(b))

residual = 1e20

# A = D + R

D = np.diag(A)

R = A - np.diag(D)

# 反復計算=>残差がトレランスより小さくなったら終了

i = 0

print('----------Start iteration----------')

while residual > tolerance:

# 解と残差を計算

x = (b - (R @ x0)) / D

residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2))

if i % 100 == 0:

print('Iteration=', i)

print('Residual=', residual)

print('x=', x)

i += 1

x0 = x

print('----------End iteration----------')

print('Iteration=', i)

print('Residual=', residual)

print('x=', x, '\n')

return x

if __name__ == '__main__':

# 係数行列と定数ベクトル

A = np.array([[2, 1, 1],

[2, 3, 1],

[1, 1, 3]])

b = np.array([2, 4, -1])

# ヤコビ法で解を反復計算

x_jacobi = jacobi(A, b, 1e-6)

print('Jacobi method x=', x_jacobi, 'Validated b=', A @ x_jacobi)

# numpyの線形代数ライブラリで検証

x_linalg = np.linalg.solve(A, b)

print('np.linalg.solve x=', x_linalg, 'Validated b=', A @ x_linalg)

Python3.9を使っているので内積の計算は@を使えています（古いバージョンはnp.dot()を使っていました）。

実行結果

上記コードを実行すると以下の結果を得ます。まずはループ100回毎に反復計算の情報を出力し、最後に何回計算したか、その残差値と得られた解を示しています。

今回は87回計算が回り、解＝[1.0000005 1.00000051 -0.99999962] を得ました。

np.linalg.solveの値（こちらも近似ですが）は[1. 1. -1.] なので、ヤコビ法も近い値を得ていることがわかります。

トレランスの値をもっと小さくとれば解の精度が上がりますが、必要な精度はどれくらいかということはいつも考えた方が良さそうです。

----------Start iteration----------
Iteration= 0
Residual= 1.2875962501274114
x= [ 0.46513241  1.04529143 -0.42239858]
----------End iteration----------
Iteration= 87
Residual= 9.800795882161607e-07
x= [ 1.0000005   1.00000051 -0.99999962] 

Jacobi method x= [ 1.0000005   1.00000051 -0.99999962] Validated b= [ 2.00000188  4.00000291 -0.99999786]
np.linalg.solve x= [ 1.  1. -1.] Validated b= [ 2.  4. -1.]

----------Start iteration----------

Iteration= 0

Residual= 1.2875962501274114

x= [ 0.46513241 1.04529143 -0.42239858]

----------End iteration----------

Iteration= 87

Residual= 9.800795882161607e-07

x= [ 1.0000005 1.00000051 -0.99999962]

Jacobi method x= [ 1.0000005 1.00000051 -0.99999962] Validated b= [ 2.00000188 4.00000291 -0.99999786]

np.linalg.solve x= [ 1. 1. -1.] Validated b= [ 2. 4. -1.]

残差の計算ももしかしたら複数回に1回という頻度でも良いかも知れません（重い計算の場合はノルム計算にかかるコストもバカにならなそう）。

まとめ

この記事では連立方程式を解く手段として、直接法と反復法の概要を説明し、反復法の一種であるヤコビ法を説明しました。

ヤコビ法の式や収束判定式とともにPythonによる実装を紹介し、最後に検証としてNumpyの線形代数ライブラリによる演算と比較をしてみました。結果は近似解として良好な解だと思います。

今回は学習とプログラムの確認が主目的だったので簡単な連立方程式を扱いましたが、そのうち大規模な計算を行う予定なので、具体的な計算コストの評価はこの後行う予定です。

ヤコビ法による反復計算は式も実装も思ったより簡単でした！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

Pythonで連立方程式をヤコビ法（反復法）で解く方法

反復法とヤコビ法の概要

直接法と反復法

反復法の使い所

反復法の注意点：収束性

ヤコビ法の漸化式

なぜ対角行列と剰余行列に分けるのか？

収束判定

連立方程式をヤコビ法で反復的に解くPythonコード

動作環境

Python環境

PC環境

サンプルコード

実行結果

まとめ

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

反復法とヤコビ法の概要

直接法と反復法

反復法の使い所

反復法の注意点：収束性

ヤコビ法の漸化式

なぜ対角行列と剰余行列に分けるのか？

収束判定

連立方程式をヤコビ法で反復的に解くPythonコード

動作環境

Python環境

PC環境

サンプルコード

実行結果

まとめ

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル