数値流体力学を学習して普段のCAEへの理解を深めたいと思います。ここでは入門レベルとして1次元移流方程式の紹介、偏微分方程式の離散化からPythonによる実装までを行います。さらにシミュレーション結果は動画で確認できるようにして理解を深めます。
こんにちは。wat(@watlablog)です。ここでは移流方程式に初期条件を与えてPythonでシミュレーションする基礎的な内容を扱います!
この記事を書いた理由
計算力学技術者試験学習のため
2022年は熱流体分野の計算力学技術者試験を受けようと思っています。
2021年12月に振動分野を1級と2級受験し幸い両方とも合格しましたが、同時受験が結構厳しかったので今年は余裕をもって2級のみを受ける予定です。
筆者は現在とある企業でCAEシミュレーションを活用した製品開発を行っています。
CAEシミュレーションというのは体系的に勉強したことがないと、手法の選定やメッシュをどう切ったら良いか、エラーの対処法や解の検証といった作業がおろそかになります(そもそも異変に気づかないレベル)。
筆者は振動分野についての実験を多くやっていましたが、熱流体分野は商用ソフトをポチポチしているレベルで実験も数えるほどしかしていません。
こりゃまずいということで、振動分野と同様にこのような記事でアウトプットを意識した学習をしていくために記事化しました。
計算力学技術者試験の概要や試験勉強、モチベーションについての感想は「計算力学技術者試験1級と2級(振動)を同時に受験して合格した感想」の記事に記載しましたので、興味のある方は是非ご覧ください。
数値計算の学習にPythonを使う理由
数値計算といえばFortranやC、C++といったコンパイラ言語が高速で動作するためよく使われます。
実際の問題に数値計算を適用する場合はこれらの言語を習得する必要があると考えます。
Pythonはインタラクティブに動作するスクリプト言語のため、高速性といった面では先に紹介した言語に引けを取ってしまいます。
しかし、記述の簡便さやNumpyの存在、外部ライブラリやユーザーの豊富さで大きなメリットがあり、科学技術計算の基本アルゴリズム学習には最適な言語だと個人的に思っています。
動画の作成も簡単にできてしまうため、計算結果の視覚的理解にも役立ちます。
是非この記事をご覧の皆様もPythonで実際に手を動かしながら数値流体力学を学んでみてください。
移流方程式の概要
移流とは?
移流(Advection)とは、流体中に存在する物質や物理量(温度等)の分布がそのままの形で移動する現象を指します。
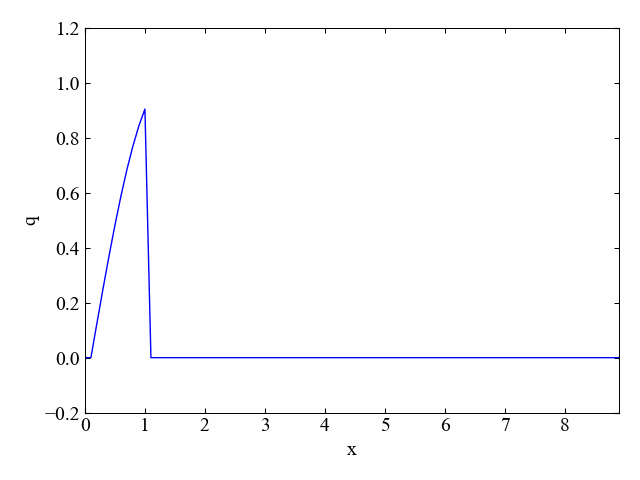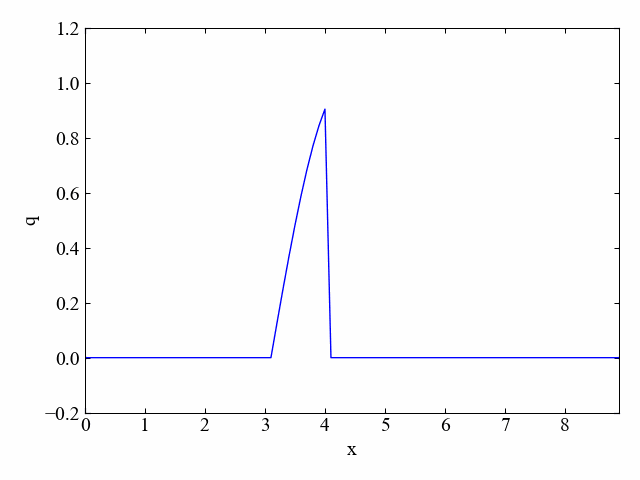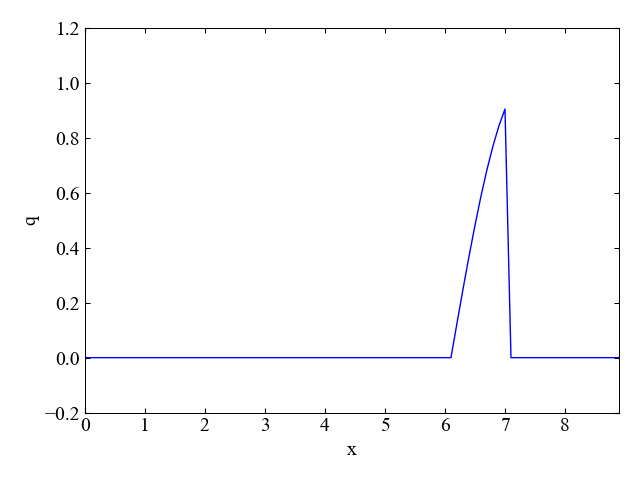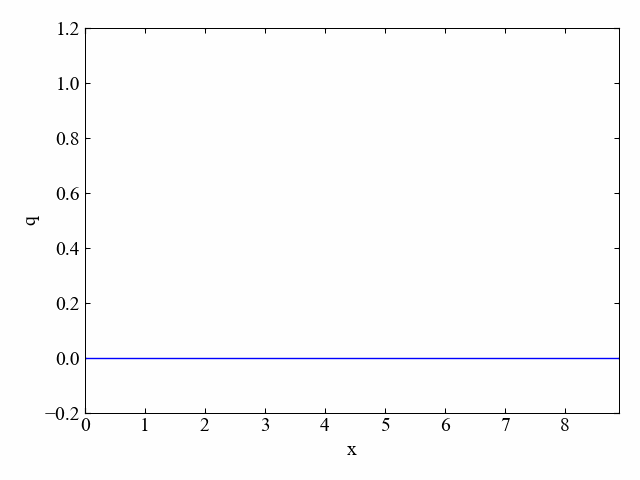
下図は横軸に空間(位置)、縦軸に物理量(任意のスカラー量)をとった時の時間進展イメージです。移流のみを扱った場合はこのように波形の形が変わらない状態で移動していく現象を扱います。
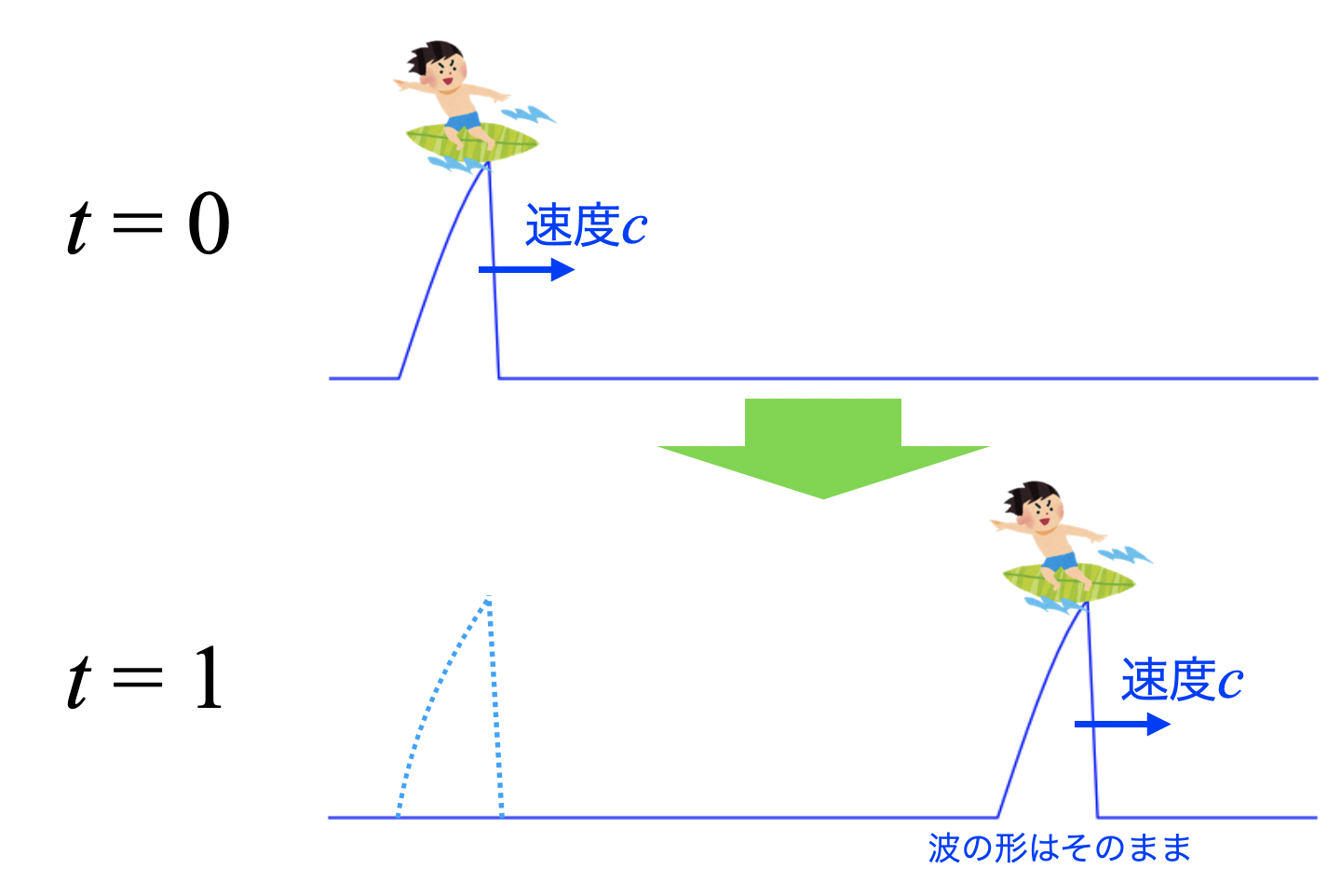
流体には色々な現象がありますが、移流は数値流体力学を学ぶ上で入門として最適です。
この記事では移流現象を記述する方程式を使って、数値流体力学の基礎となる離散化手法もいくつかまとめてみます。
Pythonを使って方程式を数値的に計算し、以下のような動画を自由に作れるようになることを目標とします。
基礎方程式
式(1)に移流方程式(Advection Equation)を示します。
ナビエ・ストークス方程式の拡散項を省略したオイラー方程式であり、移流項のみからなる偏微分方程式です。
任意の物理量\(q\)(\(u\)と書く場合も多い)、速度\(c\)、時間\(t\)、位置\(x\)から成ります。
この式(1)は速度\(c\)が一定の場合を想定して記述しているため線形で、位置は\(x\)のみであることから1次元となります。
左辺左項が時間項、左辺右項が空間項です。
厳密解
式(1)には式(2)の厳密解が存在します。
式(2)は「任意の時間\(t\)と位置\(x\)における\(q\)の分布は、\(t=0\)における分布を保ち\(ct\)だけ平行移動した形となる」という意味です。
離散化の必要性
これからPythonを使って式(1)を計算しますが、コンピュータは連続した偏微分方程式を扱うことができないため、離散化をしなければなりません。
離散化(Discretization)は式(1)の時間項と空間項それぞれに対して行う必要があります。
時間項には陽解法や陰解法、空間項には有限差分法(単に差分法とも呼ばれる)や有限体積法、有限要素法といった離散化手法があります。
今回は時間項を陽解法(前進差分)、空間項を差分法で離散化しますが、空間項の差分化スキームには様々な種類があるので次節でいくつか紹介したいと思います。
移流方程式の離散化入門とPythonコード
動作環境
このページでは以下の環境で動作確認を行ったコードを掲載しています。
動画作成の都合から画像処理ライブラリ等も使っています。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
| pillow | 7.1.2 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
時間項の離散化(共通※前進差分)
時間項に対しては前進差分を行います。
式(3)は微分形式を前進差分により離散化した結果です。
物理量\(q\)に対しては未来の値(上添字\(n+1\)が1ステップ後という意味。下添字\(j\)は\(j\)番目の格子点という意味)と現在の値(\(q^{n}_{j}\):\(j\)番目格子点の\(n\)ステップ目)で物理量の差を表現しています。
また、\(\partial t\) は\(\Delta t\)と時間の差で表現します。
後で空間の離散化と合わせて左辺に未来の値\(q^{n+1}_{j}\)のみを残し、現在の値で構成された残りを右辺に移項して方程式としますが、このように現在時刻の値を使って未来の値を予測する解法を陽解法と呼びます。
これから空間項はいくつかのバリエーション違いで結果を確認しますが、この記事における時間項に対する差分は式(3)を共通して使います。
空間差分①:1次精度風上法
離散化式
続いて空間項に対する差分の第一の例として、1次精度風上法(1st order Upwind scheme)を紹介します。風上差分、つまり後退差分を使う手法となります。
風上とは流れの上流のことを意味しています。移流現象を数値的に解く場合、主の情報は上流側からやってくるので、情報のない方向である前進差分を用いてしまうと途端に計算異常を示してしまいます。
式(4)に式(1)の空間項を風上差分で離散化した形を示します。
これで準備が整ったので、式(1)全体の離散化ができるようになりました。
式(5)に移流方程式の時間項を前進差分、空間項を1次精度風上法で離散化し、式変形した結果を示します。
式の最後で\(c \frac{\Delta t}{\Delta x}\)という形を作っていますが、この部分は無次元数でクーラン数(Courant number)と呼び、解の安定性に関わる非常に重要なファクターとなります。
注意:クーラン数が1を超えてはならない
陽解法は現在の値を使って未来の値を予測しますが、式(5)は時間だけでなく空間の情報も使って差分方程式を作っています。
この場合、クーラン数が1を超えてしまうと時間間隔\(\Delta t\)の間に情報の波が1メッシュ分(\(\Delta x\))以上伝わってしまうという因果律の破綻(式で想定した範囲外からの情報の流入)を意味してしまいます。
このようなことを避けるために式(6)とクーラン数\(\nu\)が1を超えてはならないという条件を満たす必要があります。これをCFL条件(Courant-Friedrichs-Lewy condition)と呼びます。
Pythonコード
1次精度風上法による移流方程式のシミュレーション部分を関数としてコンパクトに書いたコードを以下に示します。
この関数は1次元の格子点リストx、分布量q、時間刻みdt、格子点間距離dx、移流速度cに加え、任意の計算ステップ数stepを引数として実行します。
|
1 2 3 4 5 6 7 8 9 10 |
def sol_1d_advection(x, q, dt, dx, c, step): ''' 輸送速度が正の1次元移流方程式を数値計算する ''' for i in range(step): if i % 10 == 0: print('Iteration=', i) q0 = q.copy() for j in range(1, len(x)-1): # 時間項:前進差分/空間項:風上差分 q[j] = q0[j] - c * (dt / dx) * (q0[j] - q0[j-1]) return |
動画作成まで含めた全コードを以下に示します。
このコードを実行すると、imgフォルダに各ステップのプロット結果が画像として保存され、最後にアニメーションであるGIF動画が出力されます。
動画等要らず、最終結果だけが欲しい場合は余分な関数の実行部分をコメントアウトし、sol_1d_advectionのreturn値にqを設定してプロットすれば可能です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def sol_1d_advection(x, q, dt, dx, c, step): ''' 輸送速度が正の1次元移流方程式を数値計算する ''' dir = 'img_kaze' for i in range(step): if i % 10 == 0: print('Iteration=', i) q0 = q.copy() for j in range(1, len(x)-1): # 時間項:前進差分/空間項:風上差分 q[j] = q0[j] - c * (dt / dx) * (q0[j] - q0[j-1]) plot(x, q, i, dir) create_gif(dir, '1d_advection_kaze.gif') return def plot(x, q, i, dir): ''' シミュレーション結果をプロットし画像を保存する ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('q') # スケールの設定をする。 ax1.set_xlim(np.min(x), np.max(x)-1) ax1.set_ylim(-0.2, 1.2) # プロットを行う。 ax1.plot(x, q, label='Result', lw=1, color='blue') # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() return def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=20, loop=0) return if __name__ == '__main__': ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する ''' # 時間項の条件 dt = 0.1 # 空間項の条件 dx = 0.1 x_min = 0 x_max = 10 x = np.arange(x_min, x_max, dx) # 1次元計算格子 # 初期分布qと輸送速度c q = np.zeros_like(x) q[:int(len(x)/5)] = 1 c = 1 # クーラン数の確認 nu = c * dt / dx print('Courant number=', nu) # シミュレーションの実行 sol_1d_advection(x=x, q=q, dt=dt, dx=dx, c=c, step=100) |
実行結果:\(\nu=1.0\)
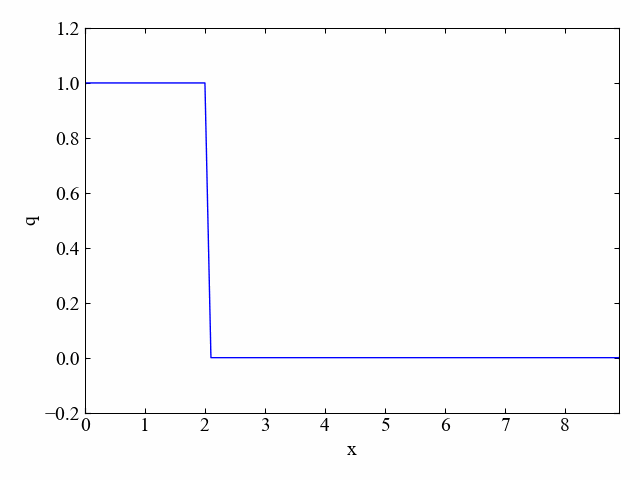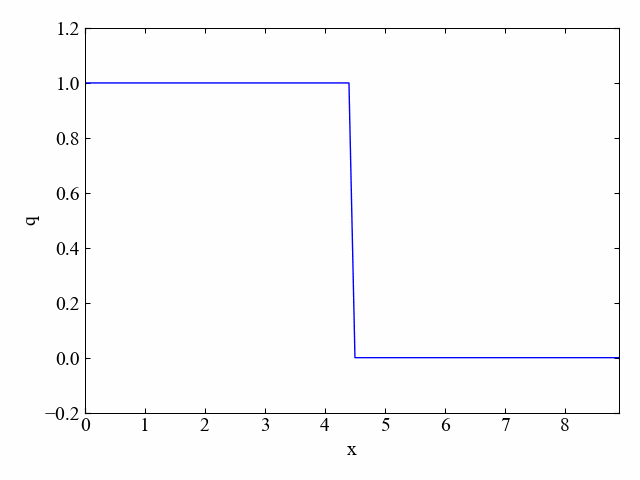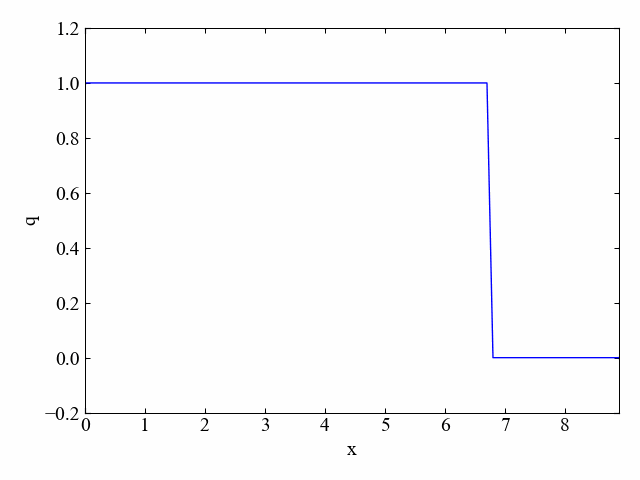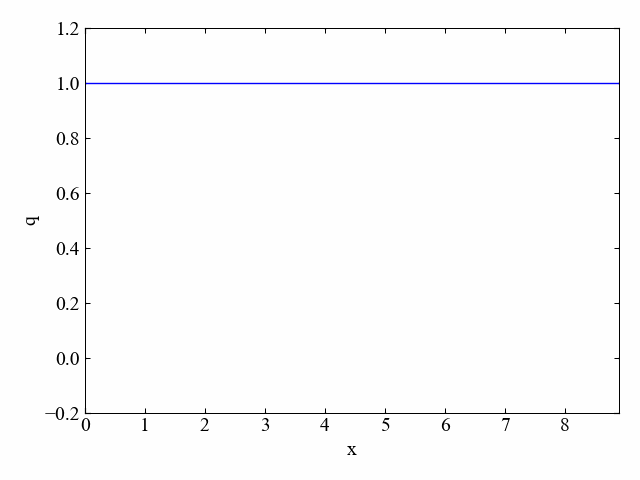
クーラン数\(\nu\)が1.0の場合(上記コードをそのまま実行した場合)は以下のシミュレーション結果が得られます。
初期の分布がそのまま平行移動するという結果は、厳密解と同じです。
実行結果:\(\nu=0. 5\)
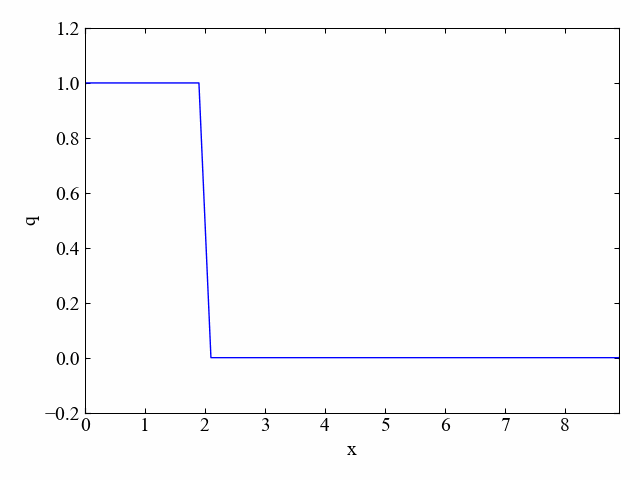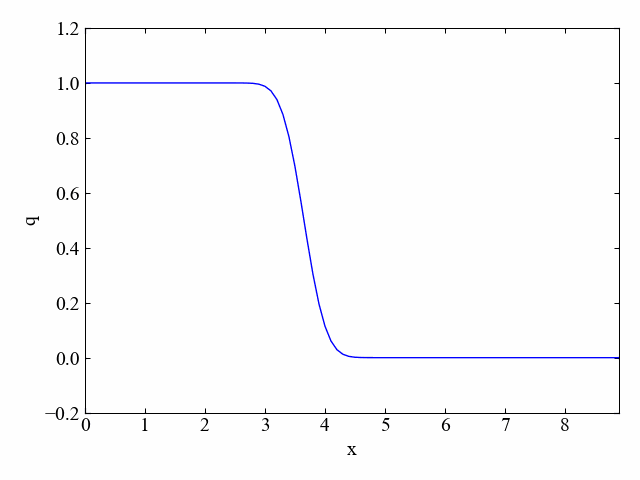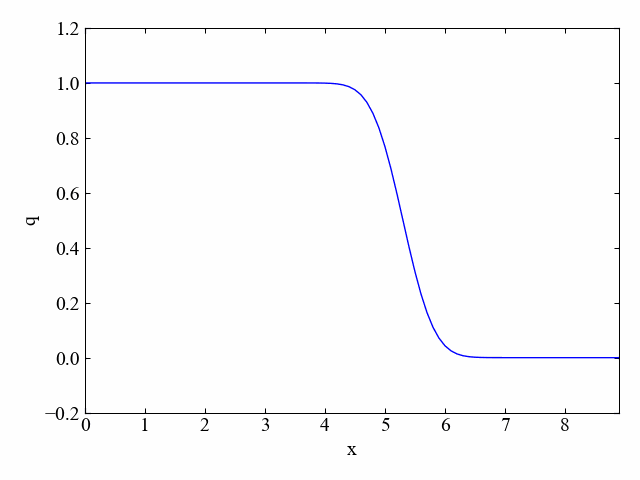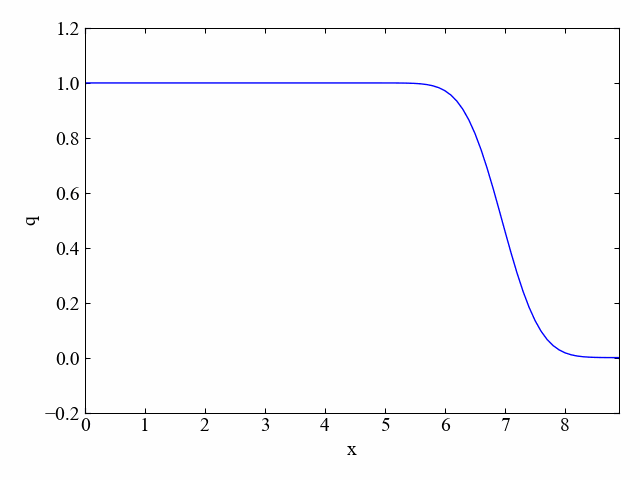
dt=0.05に変更することでクーラン数を0.5にしました。その結果がこちら。
どうやらクーラン数が1未満になると数値拡散、というか減衰が発生してだんだんと角が鈍ってくるようです。
実行結果:\(\nu=1. 5\)
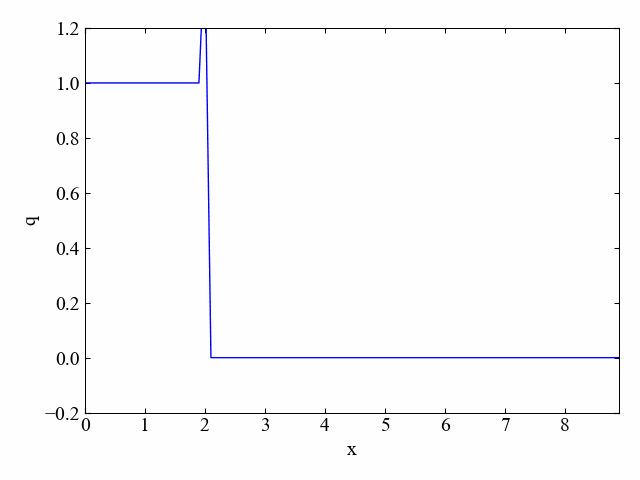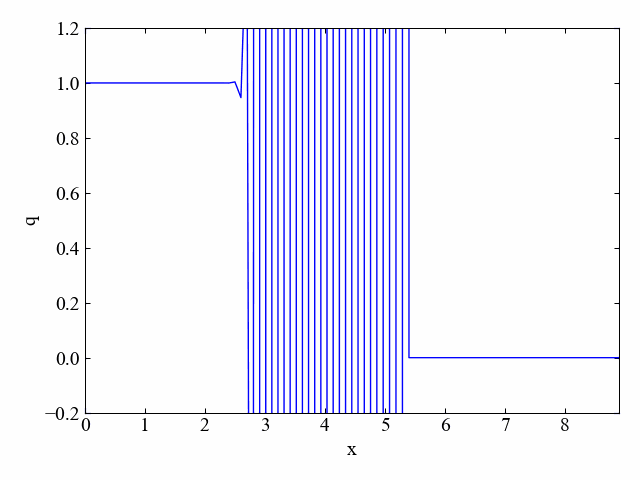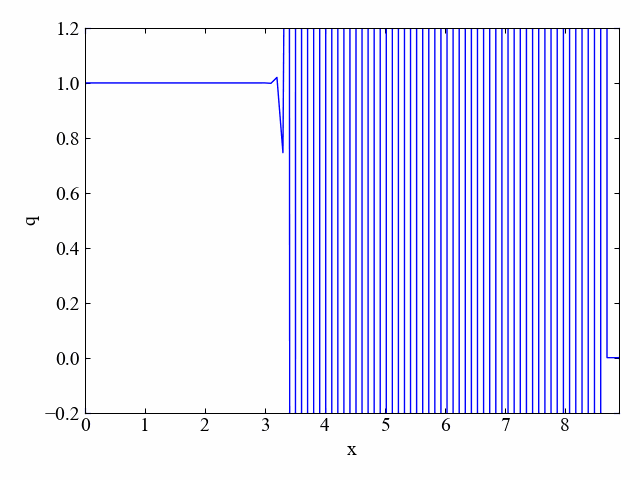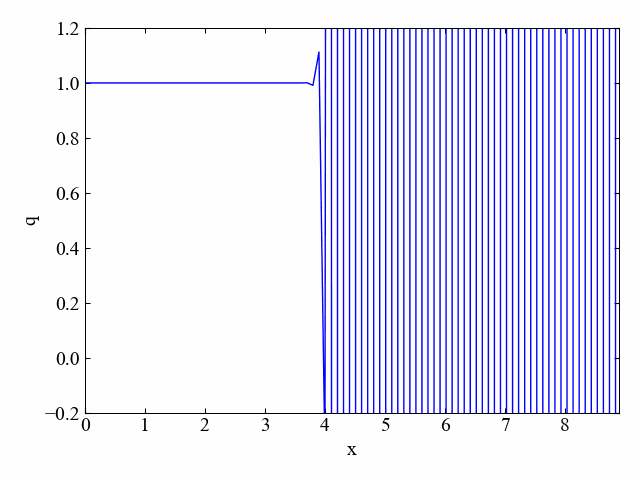
dt=0.15に変更するとクーラン数が1.5になりますが、そうするとこちら。
激しく振動しております!実際にやってみるとCFL条件を満たさないといけない理由がはっきりわかりますね。
空間差分②:FTCS法(一見良さそうだが不安定な手法例として)
離散化式
空間項の離散化について、移流であることを念頭におかなければ通常はまず初めに中心差分による離散化を考えると思います(精度良さそうという理由で)。
時間項を前進差分、空間項を中心差分で離散化して解く手法をFTCS法(Forward in Time and Centered in Space scheme)と呼びます。
空間項を中心差分法で離散化した移流方程式を式(7)に示します。
Pythonコード
Pythonコードを以下に示します。ここでは風上法の場合と比較可能とするため、q_kazeを並行計算しています。やや見にくい感は否めませんが、コピペ動作するコードということを優先します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 |
import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def sol_1d_advection(x, q, dt, dx, c, step): ''' 輸送速度が正の1次元移流方程式を数値計算する ''' dir = 'img-FTCS' # 1次精度風上法との比較用 q_kaze = q.copy() for i in range(step): if i % 10 == 0: print('Iteration=', i) q0 = q.copy() # 1次精度風上法との比較用 q0_kaze = q_kaze.copy() for j in range(1, len(x)-1): # FTCS法 q[j] = q0[j] - dt * c * (q0[j+1] - q0[j-1]) / (2 * dx) # 1次精度風上法(比較用) q_kaze[j] = q0_kaze[j] - c * (dt / dx) * (q0_kaze[j] - q0_kaze[j-1]) plot(x, q_kaze, q, i, dir) create_gif(dir, '1d_advection_FTCS.gif') return def plot(x, q1, q2, i, dir): ''' シミュレーション結果をプロットし画像を保存する ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('q') # スケールの設定をする。 ax1.set_xlim(np.min(x), np.max(x)) ax1.set_ylim(-1, 2) # プロットを行う。 ax1.plot(x, q1, label='Upwind', lw=1, color='black', linestyle='-') ax1.plot(x, q2, label='FTCS', lw=1, color='blue') ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0) # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() return def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=20, loop=0) return if __name__ == '__main__': ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する ''' # 時間項の条件 dt = 0.1 # 空間項の条件 dx = 0.1 x_min = 0 x_max = 10 x = np.arange(x_min, x_max, dx) # 1次元計算格子 # 初期分布qと輸送速度c q = np.zeros_like(x) q[:int(len(x)/5)] = 1 c = 1 # クーラン数の確認 nu = c * dt / dx print('Courant number=', nu) # シミュレーションの実行 sol_1d_advection(x=x, q=q, dt=dt, dx=dx, c=c, step=100) |
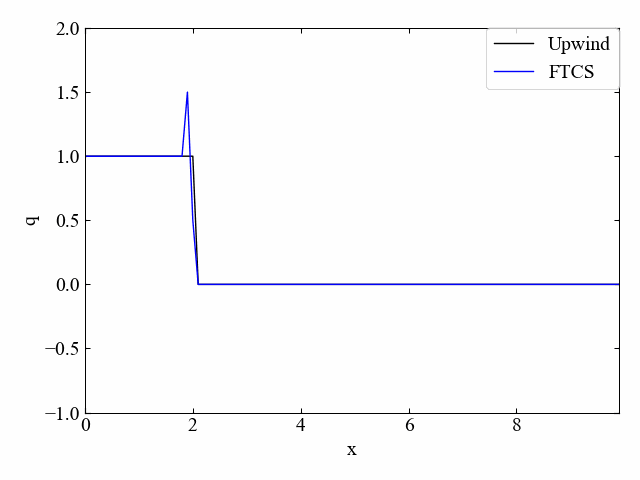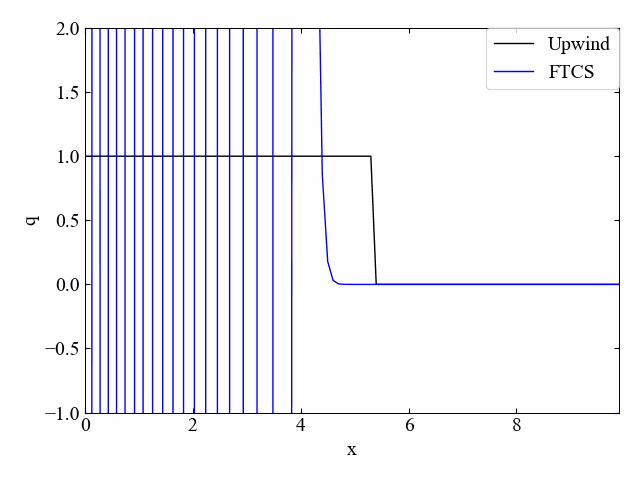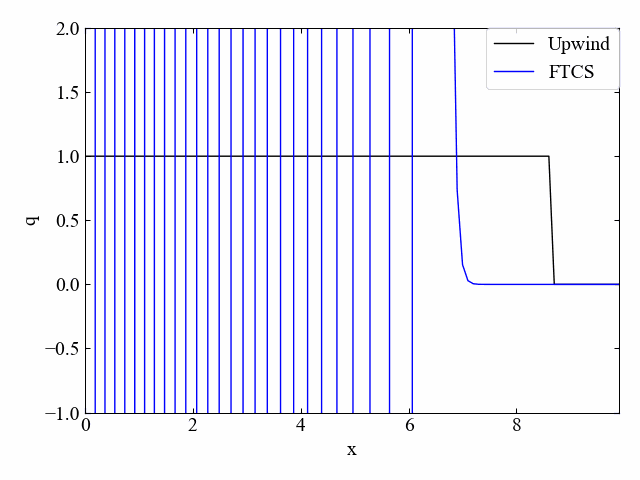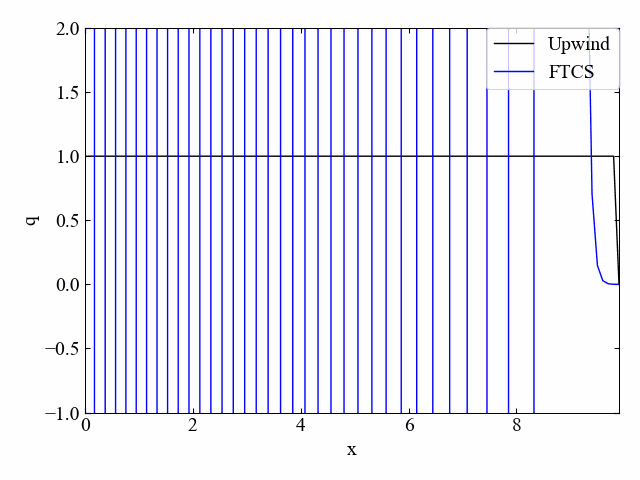
実行結果:\(\nu=1.0\)
こちらがクーラン数\(\nu=1.0\)の結果です。FTCS法はCFL条件を満たしていたとしても発散してしまいます。
実行結果:\(\nu=0.5\)
続いてこちらはクーラン数\(\nu=0.5\)の結果です。風上法は減衰していますが、FTCS法はこの条件でも発散傾向であることに変わりはありませんでした。このようにFTCS法は不安定な手法例として様々な文献\(^{[1][2]}\)で紹介されていました。
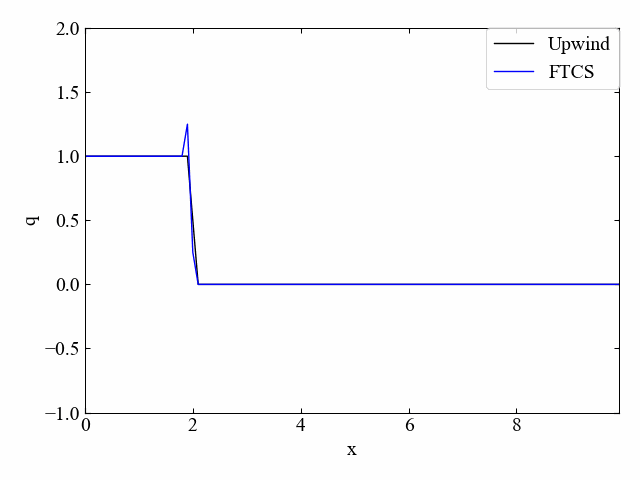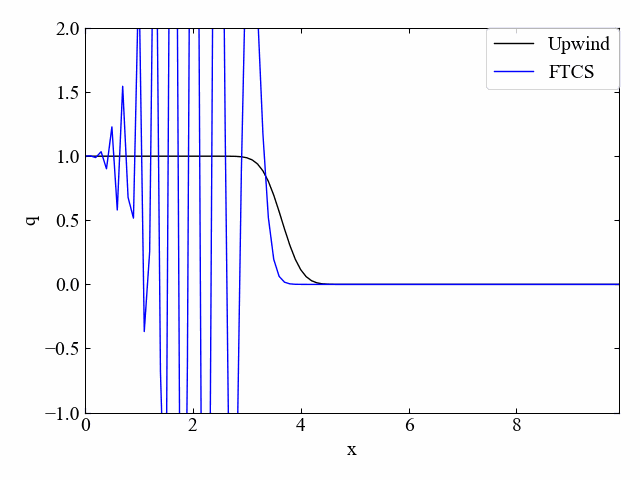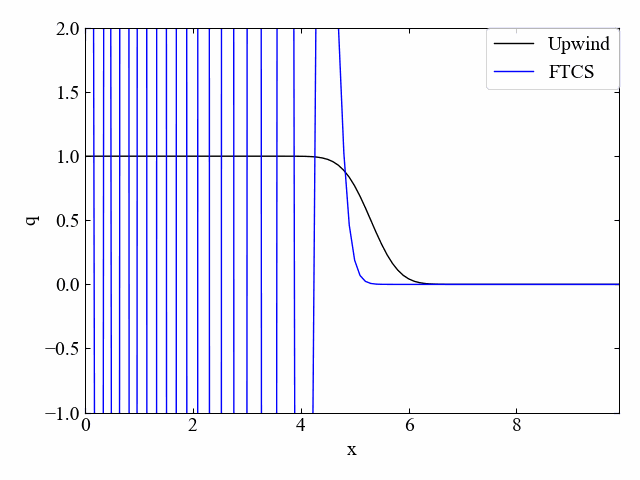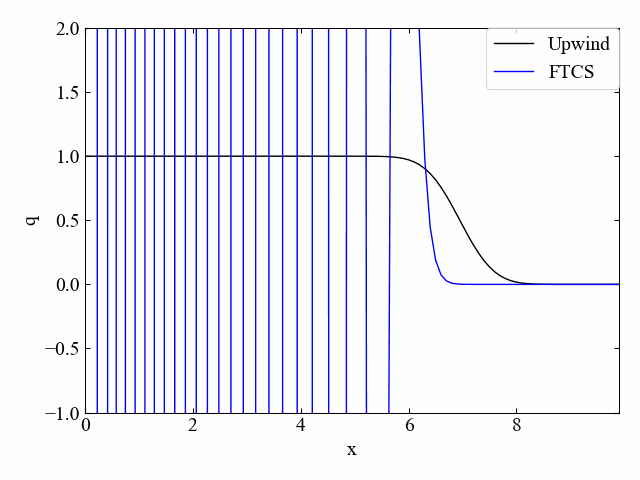
空間差分③:Lax法
離散化式
FTCS法は不安定な手法ですが、空間を後退差分より高精度な中心差分で離散化するメリットは残したい…ということで工夫されたLax法を紹介します。
Lax法(Lax-Friedrich scheme)は式(7)のFTCS法右辺左項のみを変更した式(8)で表します。
Pythonコード
Pythonコードを以下に示します。ここではLax法の特徴をよく理解するため、matplotlibのプロット軸設定と解析条件を変更、ウェーブフロントを拡大し20ステップの計算のみに限定しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 |
import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def sol_1d_advection(x, q, dt, dx, c, step): ''' 輸送速度が正の1次元移流方程式を数値計算する ''' dir = 'img-Lax' # 1次精度風上法との比較用 q_kaze = q.copy() for i in range(step): if i % 10 == 0: print('Iteration=', i) q0 = q.copy() # 1次精度風上法との比較用 q0_kaze = q_kaze.copy() for j in range(1, len(x)-1): # Lax法 q[j] = (1 / 2) * (q0[j+1] + q0[j-1]) - (c / 2) * (dt / dx) * (q0[j+1] - q0[j-1]) # 1次精度風上法(比較用) q_kaze[j] = q0_kaze[j] - c * (dt / dx) * (q0_kaze[j] - q0_kaze[j-1]) plot(x, q_kaze, q, i, dir) create_gif(dir, '1d_advection_Lax.gif') return def plot(x, q1, q2, i, dir): ''' シミュレーション結果をプロットし画像を保存する ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('q') # スケールの設定をする。 #ax1.set_xlim(np.min(x), np.max(x)) ax1.set_xlim(1.5, 3) ax1.set_ylim(-0.2, 1.2) # プロットを行う。 ax1.plot(x, q1, label='Upwind', lw=1, color='black', linestyle='-') ax1.plot(x, q2, label='Lax', lw=1, color='blue') ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0) # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() return def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0) return if __name__ == '__main__': ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する ''' # 時間項の条件 dt = 0.05 # 空間項の条件 dx = 0.1 x_min = 0 x_max = 10 x = np.arange(x_min, x_max, dx) # 1次元計算格子 # 初期分布qと輸送速度c q = np.zeros_like(x) q[:int(len(x)/5)] = 1 c = 1 # クーラン数の確認 nu = c * dt / dx print('Courant number=', nu) # シミュレーションの実行 sol_1d_advection(x=x, q=q, dt=dt, dx=dx, c=c, step=20) |
実行結果:\(\nu=1.0\)
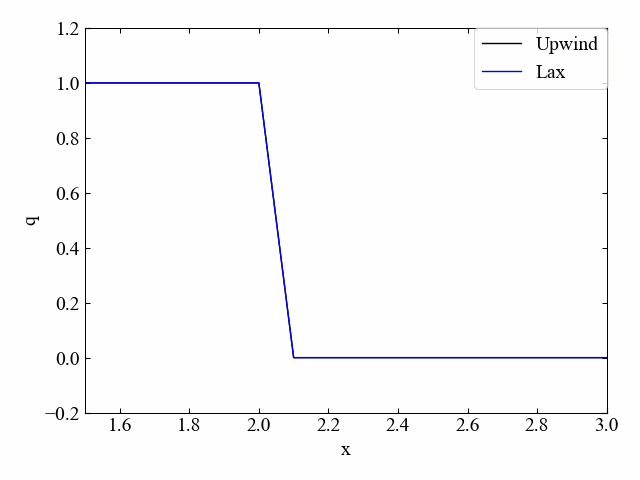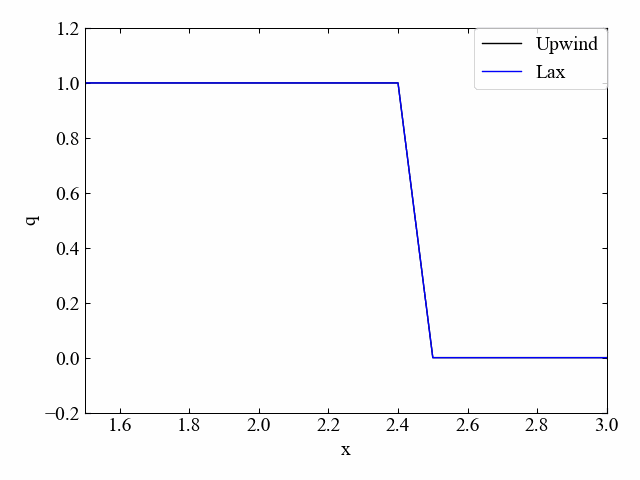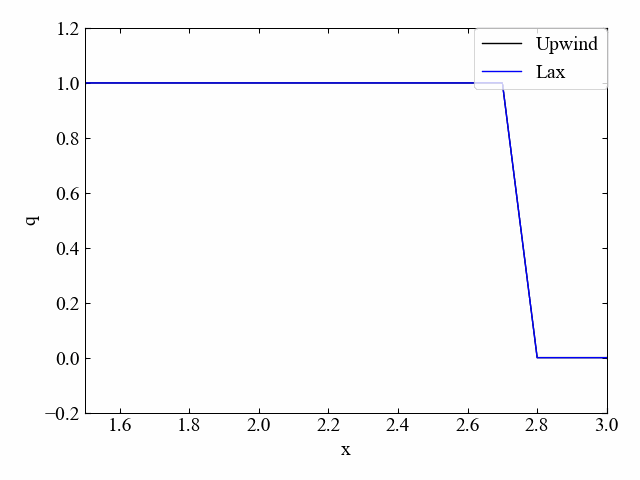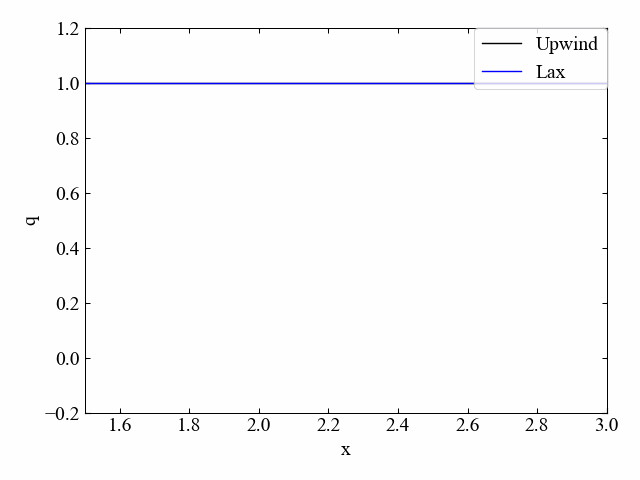
以下はクーラン数\(\nu=1.0\)の結果です。\(\nu=1.0\)であれば空間項を中心差分で離散化しつつ風上法と結果が一致しました。
実行結果:\(\nu=0.5\)
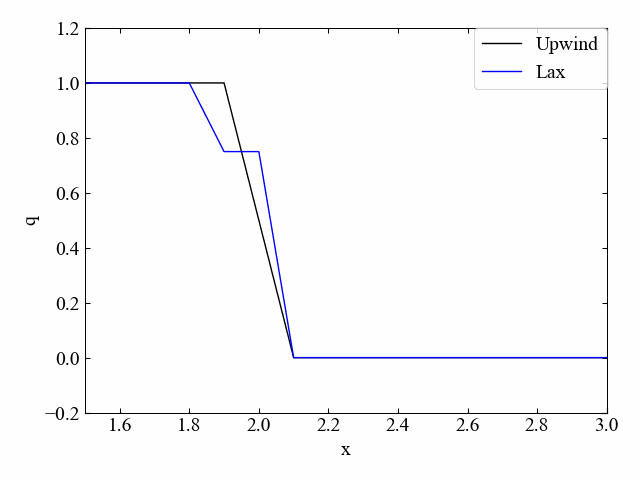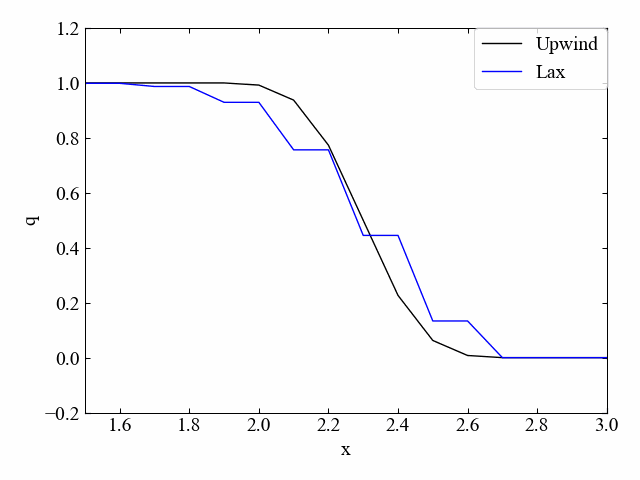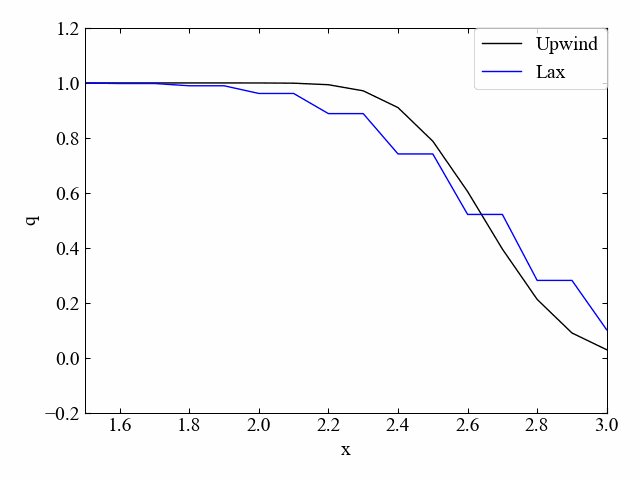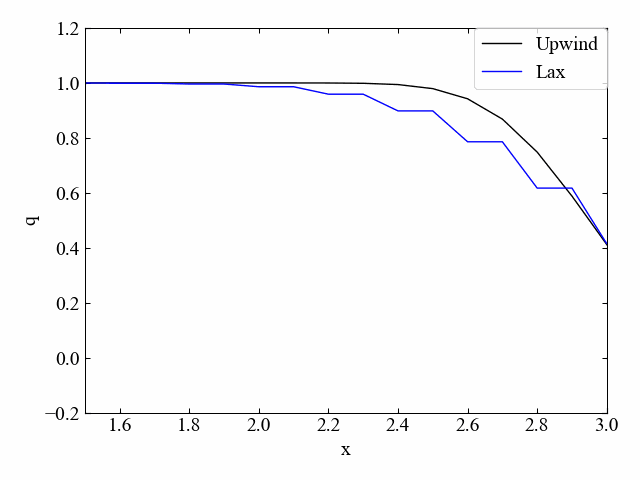
以下はクーラン数\(\nu=0.5\)の結果です。
Lax法は風上法よりも数値拡散が大きく、階段状の分布となっている結果を得ました。
式をちょっと変更するだけでこれだけ安定性が高まるのは非常に面白いですね!
空間差分④:Lax-Wendroff法
離散化式
テイラー展開に基づき、時間項と空間項を共に2次精度まで高めたLax-Wendroff法の離散化式を式(9)に示します。
Pythonコード
Pythonコードは先ほどのLax法のコード内で、sol_1d_advection()関数のみを変更するだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
def sol_1d_advection(x, q, dt, dx, c, step): ''' 輸送速度が正の1次元移流方程式を数値計算する ''' dir = 'img-Lax-Wendroff' # 1次精度風上法との比較用 q_kaze = q.copy() for i in range(step): if i % 10 == 0: print('Iteration=', i) q0 = q.copy() # 1次精度風上法との比較用 q0_kaze = q_kaze.copy() for j in range(1, len(x)-1): # Lax-Wendroff法 q[j] = q0[j] - (c / 2) * (dt / dx) * (q0[j+1] - q0[j-1]) \ + (c ** 2 / 2) * ((dt / dx) ** 2) * (q0[j+1] - 2 * q0[j] + q0[j-1]) # 1次精度風上法(比較用) q_kaze[j] = q0_kaze[j] - c * (dt / dx) * (q0_kaze[j] - q0_kaze[j-1]) plot(x, q_kaze, q, i, dir) create_gif(dir, '1d_advection_Lax-Wendroff.gif') return |
実行結果:\(\nu=1.0\)
以下動画が実行結果です。クーラン数\(\nu=1.0\)の場合は風上法と一致しています。
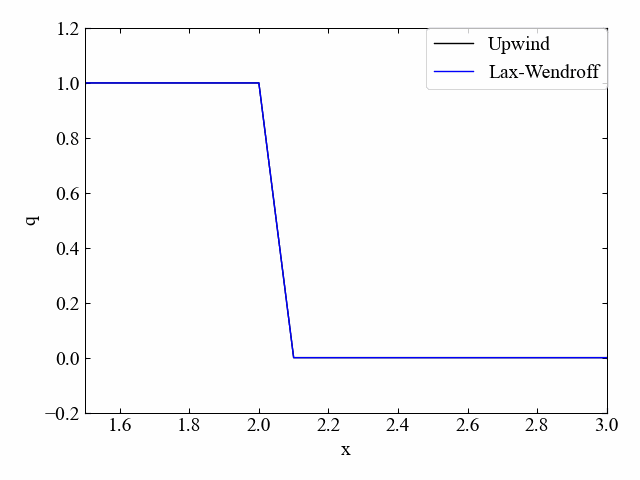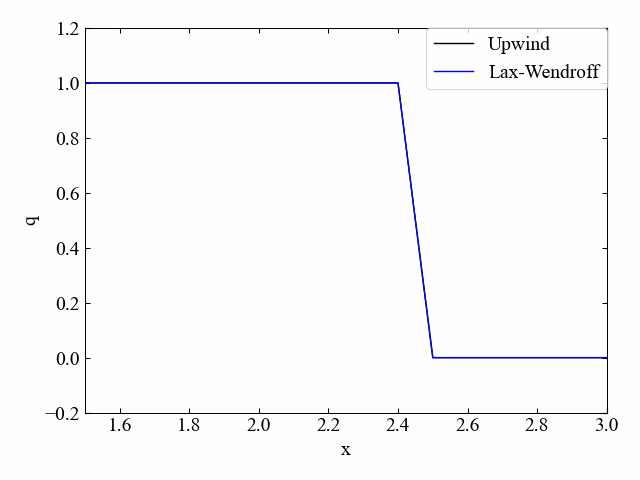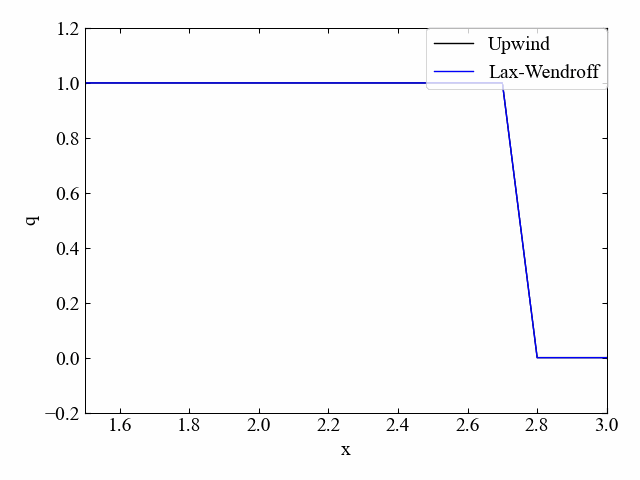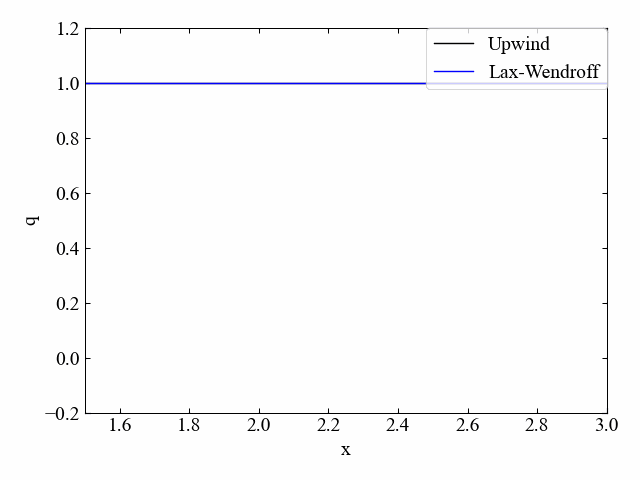
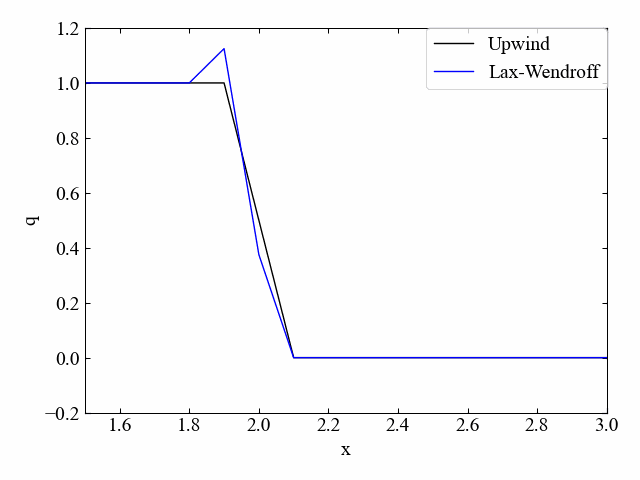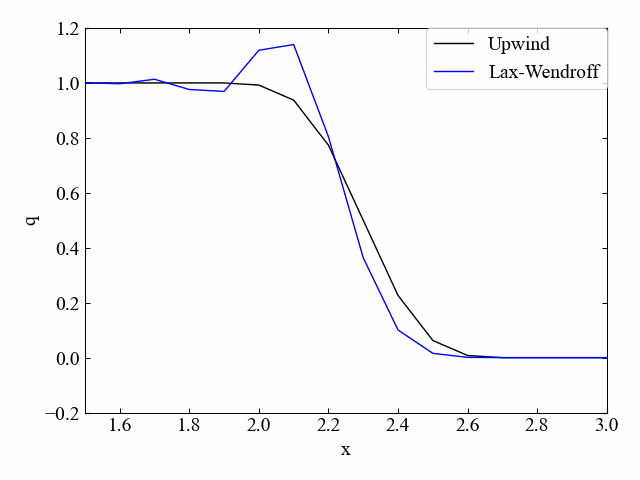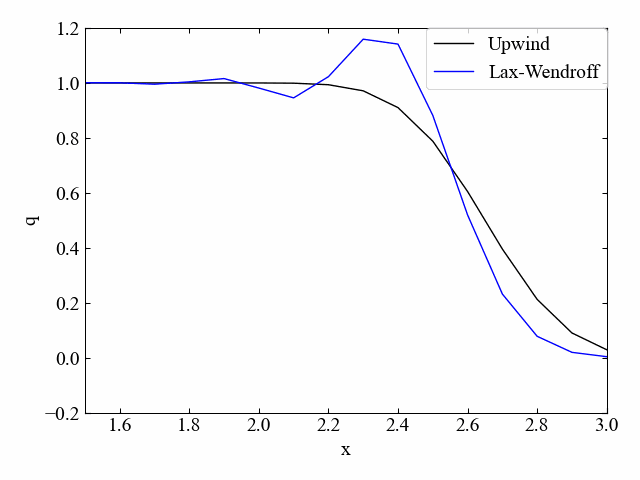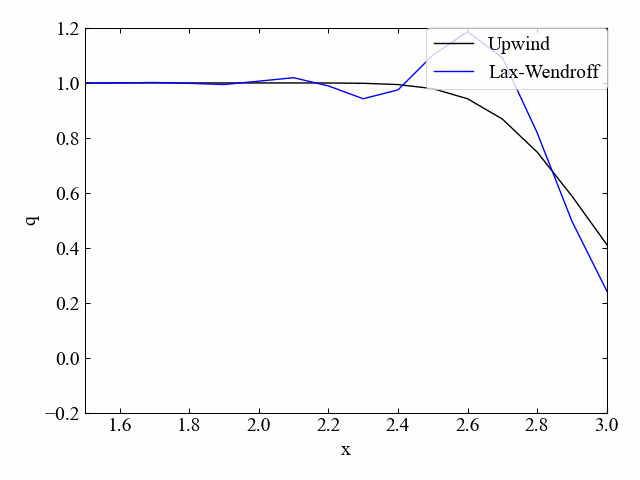
実行結果:\(\nu=0.5\)
クーラン数\(\nu=0.5\)の場合、Lax法よりも数値拡散はしなくなっています。しかし、凸部分が出てしまうという特徴も確認できました。
おまけ:速度\(c\)の向きが逆の場合
風上法は速度の向きを指定する必要がある
先ほどまではc>0の条件で統一していました。既にお気づきの方も多いと思いますが、風上法は離散化の段階で速度の向きを指定しています。そのため流れが逆になった場合はFTCS法のようにすぐに発散してしまいます。
Lax法とLax-Wendoroff法は空間項の離散化に中心差分を使っているので速度の符号がどうであれ問題はありません。
百聞は一見にしかずということで、まずは初期分布\(q\)と速度\(c\)を以下のように変更します。波形を逆順に並べ替えて、速度の符号を逆にしてみました。
|
1 2 3 4 5 |
# 初期分布qと輸送速度c q = np.zeros_like(x) q[:int(len(x)/5)] = 1 q = q[::-1] c = -1 |
ついでに凡例の位置が邪魔になるので変えておきます。
|
1 2 |
# レジェンドの位置変更 ax1.legend(bbox_to_anchor=(0, 1), loc='upper left', borderaxespad=0) |
最初はLax法と風上法(この場合は風下法と呼ぶべき?)の比較(\(\nu=0.5\))です。Lax法は先ほどの流れ方向と同じ特徴を得ましたが、風上法は予想通り発散しています。
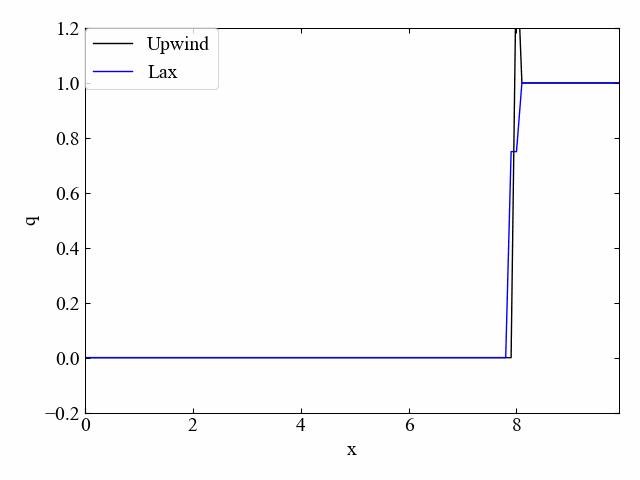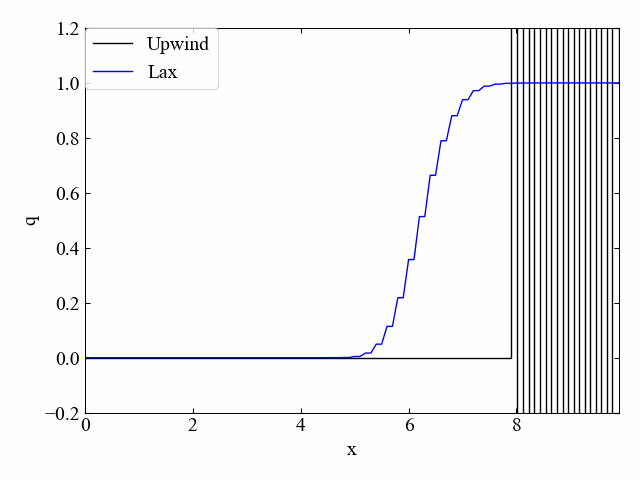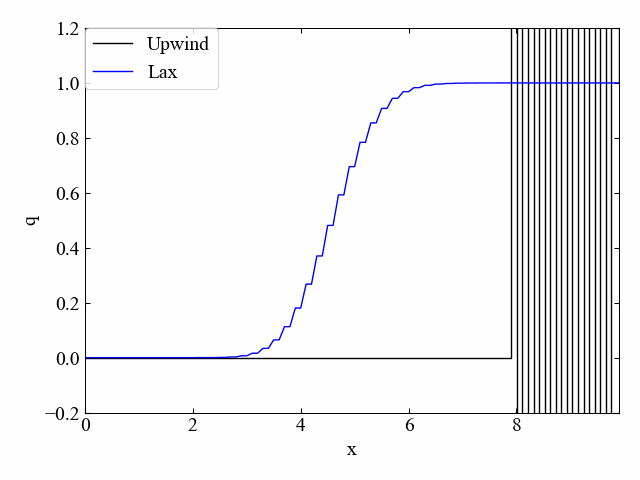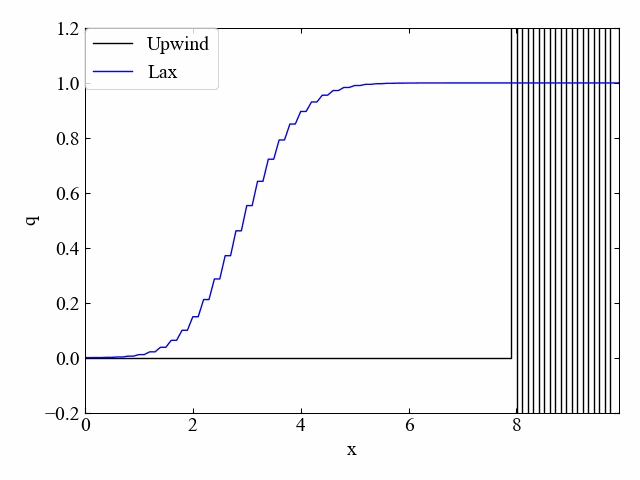
次にLax-Wendroff法と風上法の比較(\(\nu=0.5\))です。こちらも同様。
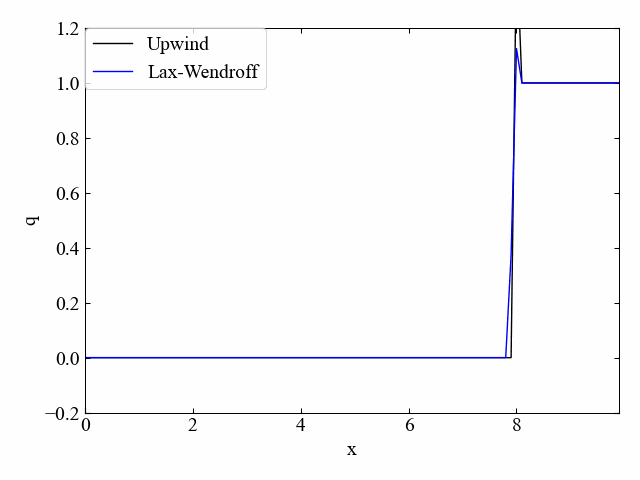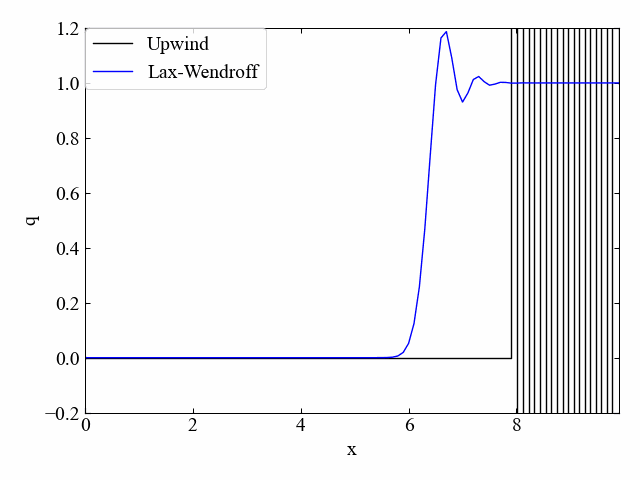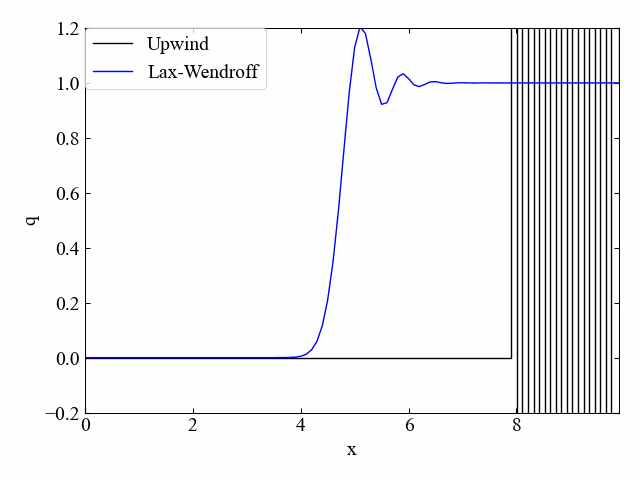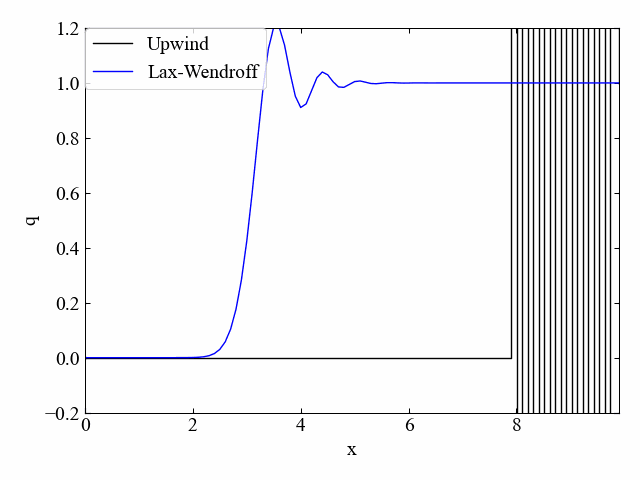
1次精度風上法を速度符号で分岐させる方法
離散化式
風上法を速度符号によらないよう修正した式を式(10)に示します。符号付きの\(c\)と絶対値の\(|c|\)を足したり引いたりして波括弧内の左右項どちらかが0になるようにすることで解決します。
0にならなかった方の速度は2倍の大きさになってしまうため、\(\frac{1}{2}\)をかけることで整合性を担保します。
Pythonコード
Lax法との比較コード内「q_kaze[j] =」の式を更新しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 |
import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob def sol_1d_advection(x, q, dt, dx, c, step): ''' 輸送速度が正の1次元移流方程式を数値計算する ''' dir = 'img-Lax' # 1次精度風上法との比較用 q_kaze = q.copy() for i in range(step): if i % 10 == 0: print('Iteration=', i) q0 = q.copy() # 1次精度風上法との比較用 q0_kaze = q_kaze.copy() for j in range(1, len(x)-1): # Lax法 q[j] = (1 / 2) * (q0[j+1] + q0[j-1]) - (c / 2) * (dt / dx) * (q0[j+1] - q0[j-1]) # 1次精度風上法(比較用) q_kaze[j] = q0_kaze[j] - (1 / 2) * (dt / dx) \ * (((c + np.abs(c)) * (q0_kaze[j] - q0_kaze[j-1])) \ + ((c - np.abs(c)) * (q0_kaze[j+1] - q0_kaze[j]))) plot(x, q_kaze, q, i, dir) create_gif(dir, '1d_advection_Lax-inverse.gif') return def plot(x, q1, q2, i, dir): ''' シミュレーション結果をプロットし画像を保存する ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('q') # スケールの設定をする。 ax1.set_xlim(np.min(x), np.max(x)) #ax1.set_xlim(1.5, 3) #ax1.set_xlim(7, 8.5) ax1.set_ylim(-0.2, 1.2) # プロットを行う。 ax1.plot(x, q1, label='Upwind', lw=1, color='black', linestyle='-') ax1.plot(x, q2, label='Lax', lw=1, color='blue') ax1.legend(bbox_to_anchor=(0, 1), loc='upper left', borderaxespad=0) # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = dir if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() return def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0) return if __name__ == '__main__': ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する ''' # 時間項の条件 dt = 0.05 # 空間項の条件 dx = 0.1 x_min = 0 x_max = 10 x = np.arange(x_min, x_max, dx) # 1次元計算格子 # 初期分布qと輸送速度c q = np.zeros_like(x) q[:int(len(x)/5)] = 1 q = q[::-1] c = -1 # クーラン数の確認 nu = c * dt / dx print('Courant number=', nu) # シミュレーションの実行 sol_1d_advection(x=x, q=q, dt=dt, dx=dx, c=c, step=100) |
修正した風上法による逆流れのシミュレーション結果がこちら。逆流れでも安定性を取り戻しました…!
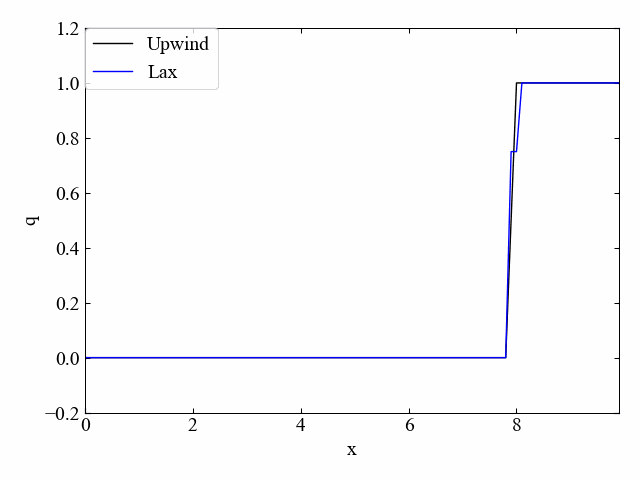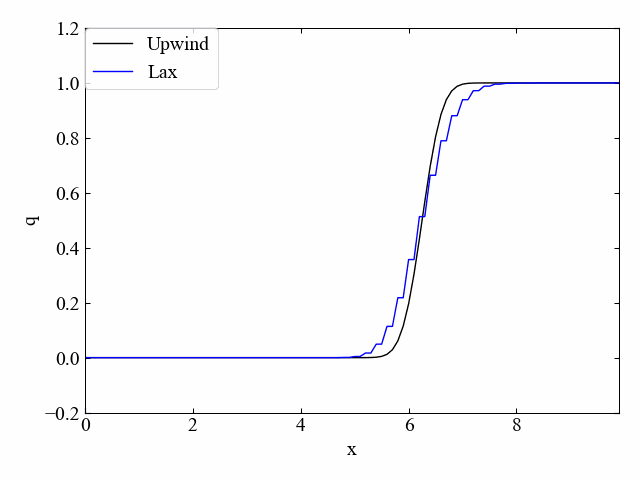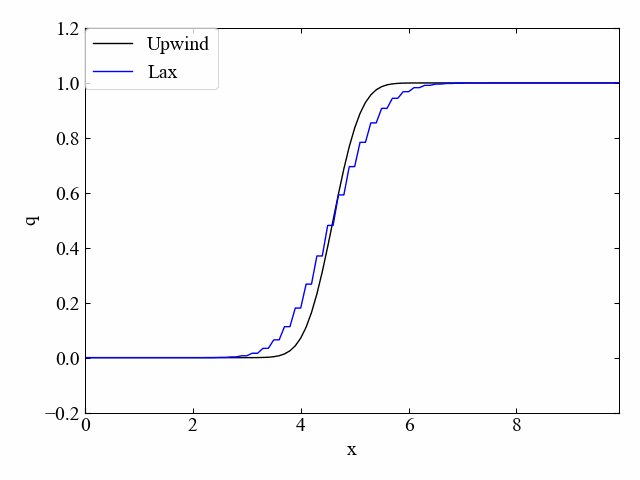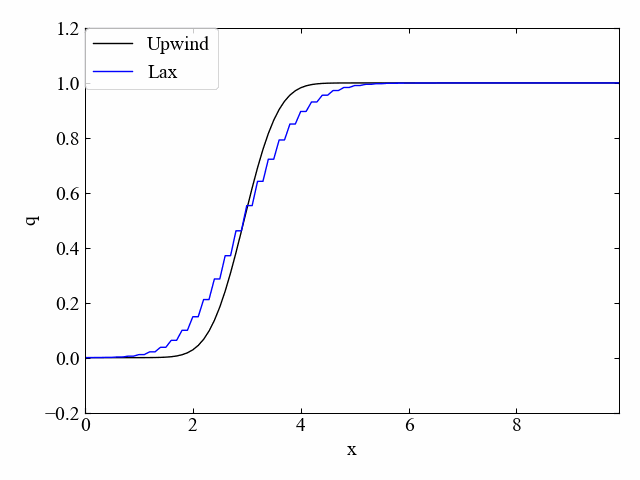
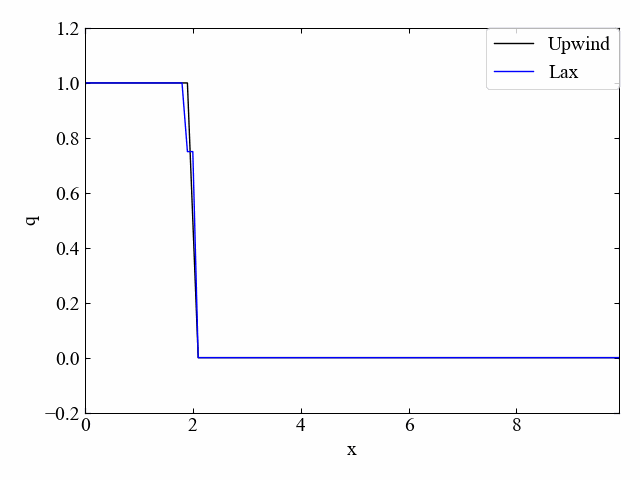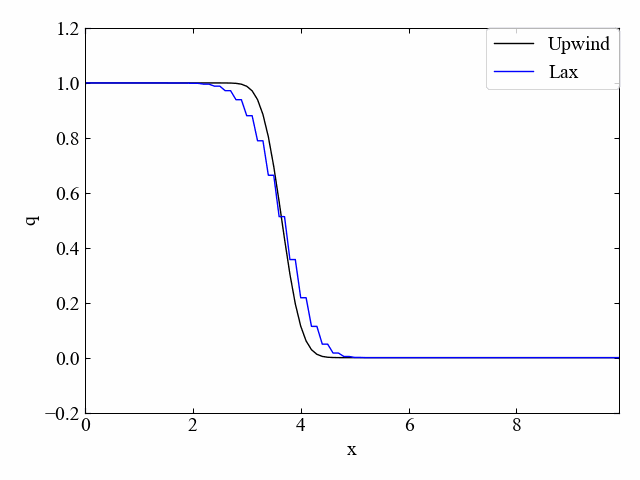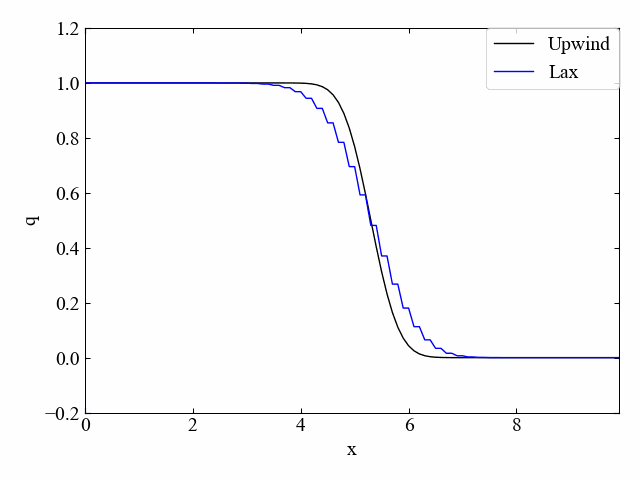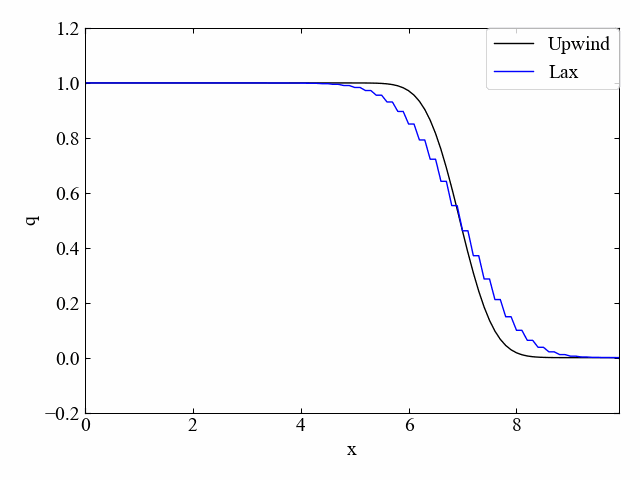
もちろん、同じコードで順方向流れにも対応しています。
まとめ
この記事では数値流体力学への入門として、移流方程式の数値計算について学んだ結果をまとめました。
移流は見た感じが簡単そうな現象ですが、差分化手法によって様々な形となることがわかりました。
差分化の方法以外にも陽解法の場合はクーラン条件を満たす必要もあることがわかりました。
今回は一連の計算を全てPythonによる動画確認で行いましたが、Pythonであれば数式をほぼそのままの形で記述することができわかりやすいと思いました。
各種差分法として「風上法」「FTCS法」「Lax法」「Lax-Wendroff法」を紹介し、風上法の場合は速度の向きによる分岐式もコードで表現してみました。
Pythonコードのシミュレーション部分は関数としていますが、メッシュ(格子座標)や初期値、解析条件を与えて実行すれば動くように意識して書いてみました(通常の商用シミュレーションソフトのような)。
計算力学技術者試験対策として書いた記事ですが、今後も熱流体分野のシミュレーションをそれほど大きく間違うことなく使えるようになるためにも継続して学習していこうと思います。
参考文献
本記事のPythonコードは筆者が色々カスタマイズしていますが、数式の展開や意味は以下の参考文献、ネット情報で学びました。
このブログではネットに載っているような基礎的な部分しか書きませんが、以下の書籍や情報は当然より詳細、多岐に渡る手法や安定性評価方法の紹介がされています。体系的に学習したい方は是非参考にしてください。
[1]藤井孝藏, 立川智章, Pythonで学ぶ流体力学の数値計算, オーム社(2020 第1版)
[2]松元亮治(千葉大学), 差分法の基礎
http://www.astro.phys.s.chiba-u.ac.jp/cans/doc/sabun.html
http://www.astro.phys.s.chiba-u.ac.jp/netlab/summer-school_2004/TEXTBOOK/text1-1.pdf
移流方程式を差分化させて解くことができるようになりました\((v \cdot \nabla)v\)
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!