
Pythonのsympyでintegrateを使うと積分式も文字式のまま処理する事が可能です。ここでは例題としてとあるホテルのWi-Fiパスワードをsympyで解きながら使い方を確認していきます。
こんにちは。wat(@watlablog)です。今回はPython/sympyの力で有名な積分問題を解いてフリーWi-Fiを使えるようにします!
sympyのおさらい
sympyについては、以下のテイラー展開やニュートン・ラフソン法を実装した記事でインストール方法から書いていますので、是非こちらもご覧ください。
Python/sympyでテイラー展開した結果をグラフ化する方法
Python/sympyとnumpyで書くニュートン-ラフソン法
積分で解くWi-Fiパスワードとは?
問題
この記事を書いた理由はTwitterのTLでとある画像が流れてきたからです。
どうやらこの画像は実在のホテル(ロンドン?)に書いてある数式のようです。
上記リンクはいつかなくなるかも知れませんので、以下LaTeX形式で書き下しておきます。
…一見すると難しそうなこの式、さてどうやって解きますか?
数式アレルギーの人は見た瞬間思考停止しそうな問題。でもこれを解けないとホテルのWi-Fiを使えない、かつWi-Fiがないのでググれない状況を設定しましょう。
但し、自分のPCにPythonとsympyはインストールされているものとする。
…という状況にしておきます(体裁)。
sympyで積分するコード
不定積分
百聞は一見にしかず。まずは比較的暗算できそうな不定積分をsympyを使って解くPythonコードを見てみましょう。
|
1 2 3 4 5 6 7 8 9 10 |
from sympy import* # 変数を定義 x = Symbol('x') # 積分形を表示 print('x:', integrate(x, x)) print('x^2:', integrate(x ** 2, x)) print('sin(x):', integrate(sin(x), x)) print('sin(2x):', integrate(sin(2 * x), x)) |
上記のように、integrate(式, 積分する変数)と書く事で、以下の結果を得ます。
|
1 2 3 4 |
x: x**2/2 x^2: x**3/3 sin(x): -cos(x) sin(2x): -cos(2*x)/2 |
合っていますね。積分定数は出してくれませんが、特に問題ないでしょう。
何度使っても、文字のまま計算してくれるsympyは数学弱者にとってありがたいです。
定積分
冒頭の問題は範囲を指定した定積分です。次は定積分を求める方法を確認します。
定積分はintegrate(式, (積分する変数, 開始値, 終了値))と、先ほど変数で指定していた部分に区間を設定する事で計算します。
以下手計算が容易な式で例題を解いてみます。
|
1 2 3 4 5 6 7 8 9 |
from sympy import* # 変数を定義 x = Symbol('x') # 積分形を表示 print('x:', integrate(x, (x, 0, 2))) print('sin(x):', integrate(sin(x), (x, 0, pi))) print('cos(x):', integrate(cos(x), (x, 0, pi))) |
こちらが結果。具体的な数値が求まりました。
|
1 2 3 |
x: 2 sin(x): 2 cos(x): 0 |
定積分結果が文字式になる場合
sympyの定積分結果が文字式になる場合、それは無理数等になっている可能性があります。その場合は以下のように近似値を出す事も一つの手段です。
|
1 2 3 4 5 6 7 8 9 10 |
from sympy import* # 変数を定義 x = Symbol('x') # 積分形を表示 print('sqrt(x):', integrate(sqrt(x), (x, 0, 2))) # 積分形から値を求める print('sqrt(x):', float(integrate(sqrt(x), (x, 0, 2)))) |
以下が結果です。
|
1 2 |
sqrt(x): 4*sqrt(2)/3 sqrt(x): 1.8856180831641267 |
Wi-Fiパスワードを求めてみる
それではいよいよホテルのWi-Fiパスワードを計算してみましょう。
コードは以下です。めちゃくちゃシンプルです。
|
1 2 3 4 5 6 7 |
from sympy import* # 変数を定義 x = Symbol('x') # 積分して値を求める print(float(integrate((x ** 3 * cos(x / 2) + (1 / 2)) * sqrt(4 - x ** 2), (x, -2, 2)))) |
結果はこちら。「The Wi-Fi password is the first 10 digits of the answer.」とあるので、「3141592653」が答えのようですね。この問題は「\(\pi\)」を求める式だったんですね。
|
1 |
3.141592653589793 |
これでこのホテルでWi-Fiが使えるようになりました。
Pythonで関数を作図して確かめてみる
せっかくなので、この問題をもう少し考察してみます。
積分は面積を求めるものなので、まずは関数の形を見てみましょう。
プロットはnumpyとmatplotlibで行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np from matplotlib import pyplot as plt x = np.arange(-2., 2., 0.01) y = (x ** 3 * np.cos(x / 2) + (1 / 2)) * np.sqrt(4 - x ** 2) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xticks(np.arange(-10, 10, 0.5)) ax1.set_xlim(-2, 2) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, y, lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
以下の関数でxが-2から2までの区間の面積を求めるというのが問題の本質です。
パッと見はよくわかりませんね。
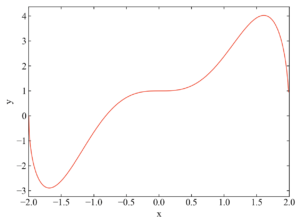
問題式は以下のように展開する事が可能です。
以下のコードで第1項\((x^{3} \cos \frac{x}{2})\sqrt{4-x^{2}}\)を可視化してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np from matplotlib import pyplot as plt x = np.arange(-2., 2., 0.01) y = x ** 3 * np.cos(x / 2) * np.sqrt(4 - x ** 2) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xticks(np.arange(-10, 10, 0.5)) ax1.set_xlim(-2, 2) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, y, lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
第1項\((x^{3} \cos \frac{x}{2})\sqrt{4-x^{2}}\)は以下の関数形となります。先ほどのフル関数と異なり、(0, 0)を中心として点対称になっています。これは奇関数といって絶対値の等しい開始値と終了値で面積を求めると0になります。
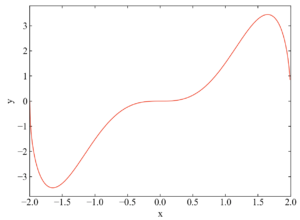
続いて以下のコードで第2項\(\frac{1}{2} \sqrt{4-x^{2}}\)をプロットしてみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np from matplotlib import pyplot as plt x = np.arange(-2., 2., 0.01) y = (1 / 2) * np.sqrt(4 - x ** 2) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xticks(np.arange(-10, 10, 0.5)) ax1.set_xlim(-2, 2) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, y, lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
下図が結果です。どうやらこの第2項\(\frac{1}{2} \sqrt{4-x^{2}}\)の関数はy=0より上で曲線(円を潰したような形)を描くようです。この面積を求める事が問題の答えとなるようですね。
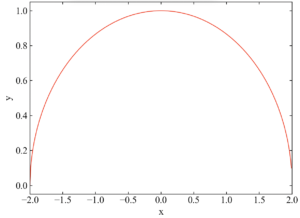
問題をおさらいすると、次式のように展開でき、第1項は0になります。
第2項の平方根部分のみをyとすると、次式のように円の方程式が出てきます。
つまり、この問題は半径2の半円の面積を求めてから1/2するという問題に落とし込む事ができるというワケですね。
まとめ
今回はネタ記事でした。sympyで積分をする記事を書きたくて、何番煎じかわからないネタを取り上げて無理やり解説してみたというものです(すみません)。
sympyは数式を記号のまま処理できる貴重なライブラリです。正しく使う事で数値誤差を極力少なくした解析もできそうなため、これからも使っていきたいと思います。
sympyによる積分の方法がわかりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!