
時間波形から微分積分演算を行う方法は有名ですが、信号処理の分野では頻繁に周波数領域を扱います。ここでは周波数軸でダイレクトに微積分する方法を紹介し、実際にPythonコードを書いて検証してみました。
こんにちは。wat(@watlablog)です。ここでは周波数軸を直接微積分する方法をPythonでコーディングします!
周波数軸で微積分するメリット
微分積分は高校数学で定義や公式を習い、式ベースで様々な関数を微積分した経験がある方が多いでしょう。
しかし、信号処理の分野では実験や解析で計測された波形を扱う事が多く、理論式が未知な場合でも微積分したい時があります。
計測された離散波形が時間波形の場合、高校数学の知識(微積分の定義)でも問題無く微積分演算を行う事ができると思います。
しかし、信号処理の分野では周波数領域の離散波形をこれまた頻繁に扱います。周波数軸で並べられたデータを微積分するのに、一回IFFT(逆高速フーリエ変換)して時間波形を求め、それから微積分する…というのは少し面倒です。
また、計測データは波形全体がオフセットしていたりドリフトしていたりしているので、低周波側の振動が結果に悪影響を与えてしまう場合が多々あります。そのため、特に積分する場合にはハイパスフィルタを使って前処理したりといった事も必要になる場合があります。
周波数軸で直接微積分演算をすることが出来れば、そのような逆フーリエ変換やフィルタ処理といった前処理をすることが無いというメリットがあります。
ここではその方法を説明し、実際にPythonコードを書いて確認をしていきます。
参考にしたページ
周波数軸微積分についてググってみると、小野測器さんのページが検索上位に来ます。今回はここに記載されている式を参考にしました(すごく簡単ですが)。
小野測器:「加速度センサからの加速度値を速度や変位に変換する方法は?」
小野測器:「周波数軸微積分」
周波数軸で微分するPythonコード
式
ある時間信号\(x(t)\)のフーリエ変換\(X(\omega)\)を周波数軸で\(n\)階微分した\(D^{(n)}(\omega)\)を式(1)で示します。
※\(\omega=2\pi f\)[Hz], \(j\)は虚数
\[
D^{(n)}(\omega)=X(\omega) (j \omega)^{n}
\tag{1}
\]
ここで、式(1)の\(X(\omega)\)はフーリエ変換後のフーリエスペクトルなので複素数です。式は乗算だけなので簡単そうですが、いくつか注意点があります。
また、パワースペクトルのような既に振幅が二乗されているスペクトルを微分する時はnの値が変わります(一階微分であればn=2, 2階微分であればn=4)ので注意が必要です。
以下に複素数の場合や周波数軸の扱い方の注意点を示しながらPythonコードを説明していきます。
Pythonコード
import文
今回の検証には以下のライブラリをimportします。
numpyはデータ準備、scipyはフーリエ変換、matplotlibはグラフプロットに使います。
|
1 2 3 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt |
サンプル波形の準備
以下の波形をサンプル波形として生成します。サンプルは\(\sin (2 \pi f t)\)で\(f=2\)です。ここでは周波数軸波形をscipyのfftpack.fftで生成し、周波数軸を同じくscipyのfftpack.fftfreqを使って生成しています。
|
1 2 3 4 5 6 7 |
# サンプル波形を作成 dt = 0.001 # 時間刻み[s] f = 2 # サンプル波形の周波数[Hz] t = np.arange(0, 1, dt) # 時間軸 original = np.sin(2 * np.pi * f * t) # 時間波形を生成 spec = fftpack.fft(original) # フーリエ変換を実行してスペクトルを得る freq = fftpack.fftfreq(len(spec), d=dt) # 周波数軸を作成(負の周波数まで必要) |
fftpack.fftfreqはフレームサイズ(時間波形のデータポイント数)と時間刻みを引数として周波数軸を生成します。当WATLABブログでは過去に「PythonでFFT!SciPyのFFTまとめ」で簡易的に周波数軸を作成していましたが、この関数を使って作るものが正式です。
以下にfreqで作られた周波数軸を示します。今回はフレームサイズが1000のデータをフーリエ変換していますが、このようにナイキスト周波数で折り返され、負の周波数軸が計算されていることが確認出来ます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. ・ ・ 468. 469. 470. 471. 472. 473. 474. 475. 476. 477. 478. 479. 480. 481. 482. 483. 484. 485. 486. 487. 488. 489. 490. 491. 492. 493. 494. 495. 496. 497. 498. 499. -500. -499. -498. -497. -496. -495. -494. -493. -492. -491. -490. -489. -488. -487. -486. -485. ・ ・ -28. -27. -26. -25. -24. -23. -22. -21. -20. -19. -18. -17. -16. -15. -14. -13. -12. -11. -10. -9. -8. -7. -6. -5. -4. -3. -2. -1.] |
式(1)には周波数情報が入っているので、この負の周波数まで考慮しないと正しく微積分演算をする事が出来ません。
ちなみに、この時点のoriginalで宣言した時間波形とそのフーリエスペクトルspecを以下の図に示します。プロットしてみると、0[Hz]で折り返された鏡像ピークが見えることがわかります。
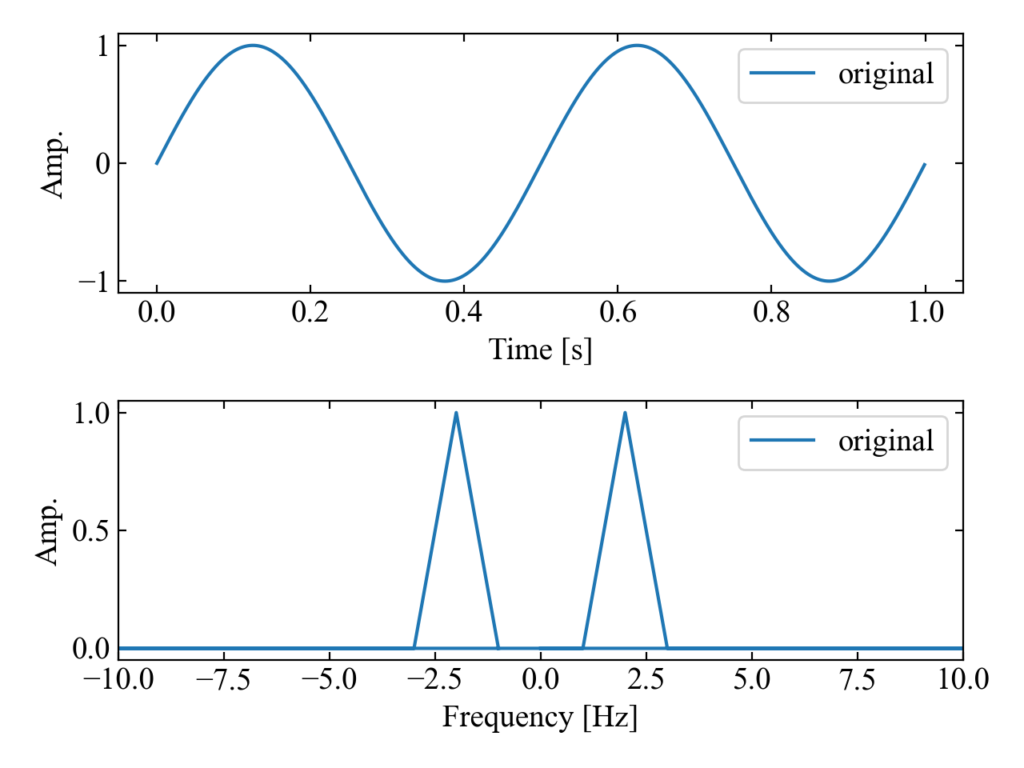
周波数軸で微分する関数
以下に周波数軸で微分する関数を示します。式(1)そのままですが、虚数は1jと与えている所に注意。
この関数はフーリエスペクトルfftと周波数軸freq、そして微分階数nを受け取り動作します。
|
1 2 3 4 5 |
# 周波数軸微分の関数(fft=フーリエ変換後のデータ(複素数), freq=周波数軸, n=階数) def differential(fft, freq, n): omega = 2 * np.pi * freq # ω=2πf diff = fft * (1j * omega) ** n # n階微分:X(f)*(jω)^n return diff |
全コード(理論値と比較)
グラフプロットまで含めた全コードを以下に示します。今回は\(n=1\)と一階微分をしてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt # 周波数軸微分の関数(fft=フーリエ変換後のデータ(複素数), freq=周波数軸, n=階数) def differential(fft, freq, n): omega = 2 * np.pi * freq # ω=2πf diff = fft * (1j * omega) ** n # n階微分:X(f)*(jω)^n return diff # サンプル波形を作成 dt = 0.001 # 時間刻み[s] f = 2 # サンプル波形の周波数[Hz] t = np.arange(0, 1, dt) # 時間軸 original = np.sin(2 * np.pi * f * t) # 時間波形を生成 spec = fftpack.fft(original) # フーリエ変換を実行してスペクトルを得る freq = fftpack.fftfreq(len(spec), d=dt) # 周波数軸を作成(負の周波数まで必要) # 周波数軸微分を実行 diff_spec = differential(spec, freq, 1) # 検証(周波数軸微分した結果のIFFTと理論波形を比較) ifft_diff_spec = fftpack.ifft(diff_spec).real theory = (2 * np.pi * f) * np.cos(2 * np.pi * f * t) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(8, 4)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amp.') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, theory, label='theory', lw=5) ax1.plot(t, ifft_diff_spec, label='differential from fft', color='red') ax1.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
以下のグラフがアウトプットです。\(\sin (\omega t)\)を微分しているので、理論波形は合成関数の微分により\(\omega\cos (\omega t)\)となり、周波数\(f\)が2なので振幅は\(2 \pi f)\)となります。
グラフは理論波形と、\(\sin (\omega t)\)を周波数軸で微分した結果をIFFTで時間波形に復元したものを重ねた結果です。
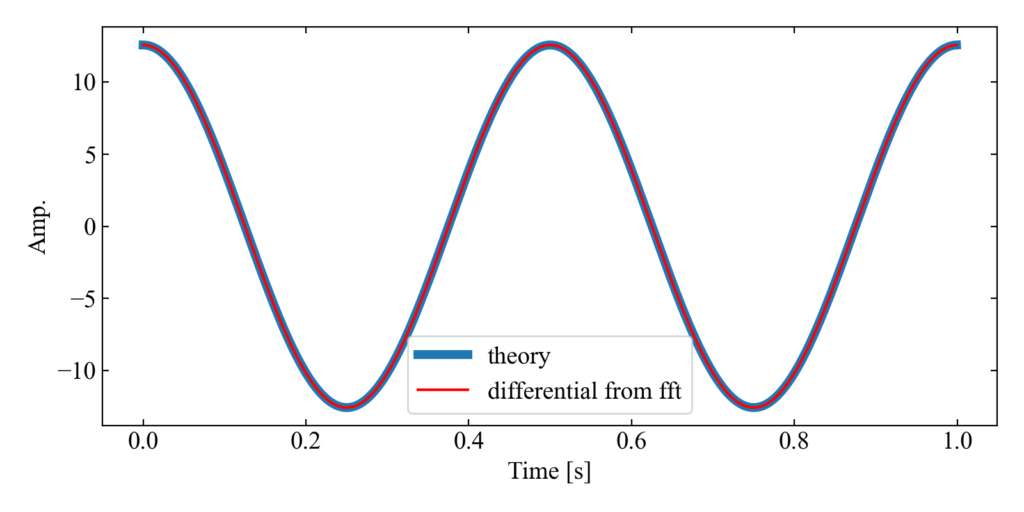
見事\(\omega\cos (\omega t)\)と重なっています(虚数の作用(位相をずらす)を考えて式を見れば当たり前なのですが、フーリエ変換に演算を加えて微分できた事に地味に感動)。
周波数軸を正しく算出していない等の場合は時間波形にした段階で理論波形と一致しません。
周波数軸で積分するPythonコード
式
ある時間信号\(x(t)\)のフーリエ変換\(X(\omega)\)を周波数軸で\(n\)重積分した\(I^{(n)}(\omega)\)を式(2)で示します。
※\(\omega=2\pi f\)[Hz], \(j\)は虚数
\[
I^{(n)}(\omega)=X(\omega) \frac{1}{(j \omega)^{n}}
\tag{2}
\]
注意点等は先ほどの微分の場合と同様なので省略します。
Pythonコード
周波数軸で積分する関数
Pythonコードは関数部分のみ変更します。以下が周波数軸で積分する関数です。最初の行にfreq[0]=1と入っていますが、これは周波数軸の最初の要素は必ず0であり、このまま式(2)で積分をかけると分母に0を含んでしまう事を回避したものです(もっとうまい回避あれば教えて下さい…)。
|
1 2 3 4 5 6 |
# 周波数軸積分の関数(fft=フーリエ変換後のデータ(複素数), freq=周波数軸, n=重数) def integral(fft, freq, n): freq[0] = 1 #0割り回避用の代入(もっとうまい回避あれば教えて) omega = 2 * np.pi * freq # ω=2πf integral = fft * (1 / (1j * omega) ** n) # n重積分:X(f)*(1/(jω)^n) return integral |
全コード(理論値と比較)
コピペ用、理論値比較用の全コードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt # 周波数軸積分の関数(fft=フーリエ変換後のデータ(複素数), freq=周波数軸, n=重数) def integral(fft, freq, n): freq[0] = 1 #0割り回避用の代入(もっとうまい回避あれば教えて) omega = 2 * np.pi * freq # ω=2πf integral = fft * (1 / (1j * omega) ** n) # n重積分:X(f)*(1/(jω)^n) return integral # サンプル波形を作成 dt = 0.001 # 時間刻み[s] f = 2 # サンプル波形の周波数[Hz] t = np.arange(0, 1, dt) # 時間軸 original = (2 * np.pi * f) * np.cos(2 * np.pi * f * t) # 時間波形を生成 spec = fftpack.fft(original) # フーリエ変換を実行してスペクトルを得る freq = fftpack.fftfreq(len(spec), d=dt) # 周波数軸を作成(負の周波数まで必要) # 周波数軸積分を実行 integral_spec = integral(spec, freq, 1) # 検証(周波数軸積分した結果のIFFTと理論波形を比較) ifft_integral_spec = fftpack.ifft(integral_spec).real theory = np.sin(2 * np.pi * f * t) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(8, 4)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amp.') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, theory, label='theory', lw=5) ax1.plot(t, ifft_integral_spec, label='integral from fft', color='red') ax1.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
以下が結果です。見事理論波形と周波数軸で積分した波形は重なりました。

今回は\(\omega\cos (\omega t)\)を積分して\(\sin (\omega t)\)と重なったことを確かめました。
まとめ
本記事では時間波形上の微積分ではなく、周波数波形(つまり複素数)上で虚数と振動数による微積分演算を紹介し、実際にPythonでコーディングしてみました。
簡単な三角関数を事例に、周波数軸で微積分した結果と手計算の結果が一致する所までを確認しました。
実際に使う時はまずはじめに変位や速度、加速度を個別に計測し、本プログラムで本当に想定通りの結果が得られるか…という検証が別途必要かと思います。
しかしながら、このような簡単な式で微積分ができるという事は普段のデータ分析の武器になるかなと思いました。複素数は色々できて便利ですね。
是非FFT結果は振幅成分だけでなく、実部と虚部といった複素数で残しておきましょう。
周波数軸微積分ができました!複雑な波形にはまだ適用していませんが、複素数って面白い!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
スペクトログラムからバンドごとに標準偏差を求める方法を紹介して欲しいです。
ご訪問ありがとうございます。
「バンドごとに標準偏差を求める」というのは、例えば100[Hz]-200[Hz]と、ある帯域を任意で決めて標準偏差を計算したいという事でしょうか?