Python機械学習！scikit-learnによる重回帰分析

Pythonで機械学習をする第一歩として、過去に単一の説明変数から目的変数を予測する単回帰分析を習得しました。今回は同じくscikit-learnを使って複数の説明変数を扱う重回帰分析を紹介します。

こんにちは。wat(@watlablog)です。
線形回帰問題の第2段、Pythonによる重回帰分析コードを習得しましょう！

目次（項目クリックでジャンプできます）

重回帰分析で複数変数のフィッティングができる

重回帰分析の概要

回帰分析（Regression）とは、変数間の関係を関数で表現することであることは前回の「Python機械学習！scikit-learnによる単回帰分析」で説明した通りです。

単回帰分析の場合はたった1つの説明変数で目的変数を予測する方法でした。
一方、重回帰分析は複数の説明変数で目的変数を予測する手法です。

以下の式(1)は目的変数\(y\)と\(n\)個の説明変数\(x_{n}\)の関係を示しています。説明変数にかかっている\(w_{1}\)～\(w_{n}\)は各説明変数の重みを意味する係数で、偏回帰係数と呼ばれます。\(w_{0}\)は定数項で切片を意味します。

\[y=w_{0}+w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n}　(1)\]

式(1)をもっとすっきり書くと式(2)となり、これが重回帰の一般式です。

\[y=w_{0}+\sum_{i=1}^{n}w_{i}x_{i}　(2)\]

\(n=1\)の場合は単回帰になり、直線の式になります！

重回帰分析はこの定数項\(w_{0}\)と偏回帰係数\(w_{n}\)を求めることを言いますが、その方法は当WATLABブログの「Pythonでカーブフィット！最小二乗法で直線近似する方法」で紹介した最小二乗法を使うことが一般的です。

変数の数が増えても、非線形になっても、基本的にはフィッティングさせる元となる式を用意し、データポイントとの二乗誤差が最小になるような微分の計算をすることに変わりはありません。

重回帰分析はExcelの「分析ツール」でも簡単に実行することができます。しかしここでは機械学習やその他アプリケーションへの応用を考え、Pythonによるコーディング習得を目標とします！

重回帰分析の活用例

重回帰分析はいったいどのような場面で活用されるのでしょうか？

単回帰分析は直線の式で近似するため、おそらく義務教育課程の学生からデータを扱う多くの方が日々利用していることでしょう。

しかし重回帰分析も活用方法は同じです。説明変数が1つであろうと複数であろうと何かを予測したい時に使うということには変わりはありません。

説明変数が3つ以上ある場合は図示することが困難になります。2つの説明変数からなる重回帰分析は平面にフィットさせることと同じなので、まずは2つの説明変数の重回帰分析の例をこれから説明します。

実験結果、シミュレーション結果を始めとした各種データは、色々な条件を振って結果を得ることをよくします。

以下の図は、ある説明変数\(x_{1}\)と\(x_{2}\)という二つの条件を変えた時の目的変数\(y\)を得た結果を示しています。

ここで、まだ試していない新しい条件（新しい\(x_{1}\)と\(x_{2}\)の組み合わせ）の\(y\)値を知りたい場合、その実験をもう一度やるしかないのでしょうか？

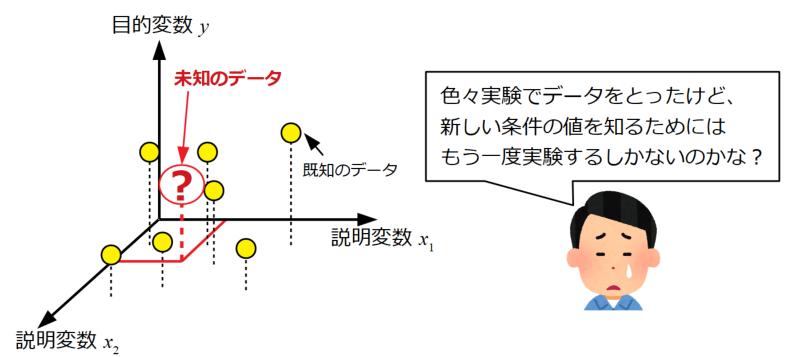
一般的に実験とは設備を用意したり、セットアップをしたり…適切な知識が必要だったりと人も物もお金もかかります。できれば実験をしないで値を予測できた方が良いと考えます。

上記のような2つの説明変数の場合に重回帰分析を用います。
仮に実験データが線形の変化をしていた場合は予測モデルを平面(\(y=w_{0}+w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n}\))で立てることが出来ます。

モデル（式）が出来れば、まだ測定したことのない変数の組み合わせを代入することで目的である未知のデータの値を予測することが可能になります。

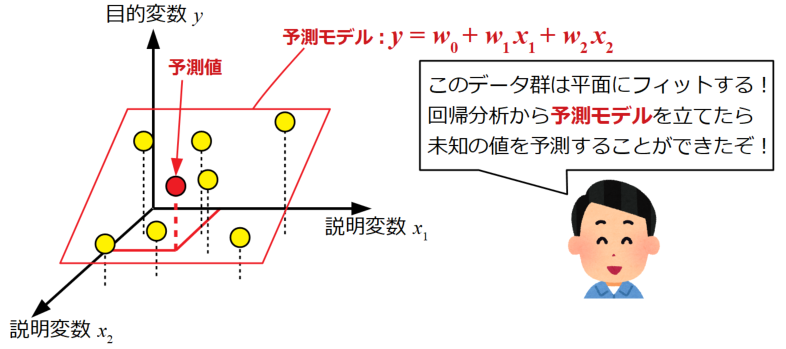
今回は2つの説明変数の例を示しましたが、説明変数がいくつになってもこの考え方は変わりません。

もちろん現象に非線形性が含まれていて平面ではどうやってもフィットできない場合も多々ありますが、このページで扱う線形重回帰分析の活用方法として一例を挙げました。

重回帰分析のノウハウ

重回帰分析の概要はわかってきたと思います。これだけでも重回帰分析をすることはできますが、この計算には他にもテクニックや注意しなければいけない点がありますので、その内容をメモしておきます。

標準偏回帰係数の利用で影響度分析ができる

式(2)において、偏回帰係数を使うと実際の物理量の単位とそのまま関係を持つので大変理解しやすくよく使われます。

しかし、データを取得した時の単位の違い（体重であれば[g]と[kg]）によって偏回帰係数は異なる値をとってしまいます。

さらに、重回帰分析は複数の変数を扱うため、変数間の影響度（目的変数に対する変化をどれだけ与えるかという指標）を分析することも重要です。

影響度の分析をする時には、予めデータセットを標準化しておきます。標準化については「Python/sklearnで学習データの前処理！標準化と正規化」で紹介しましたので、是非参照下さい。

標準化されたデータを使って得られた変数にかかる重みは標準偏回帰係数\(w_{std}\)と呼ばれ、通常の偏回帰係数\(w\)と説明変数の標準偏差\(\sigma_{x}\), 目的変数の標準偏差\(\sigma_{y}\)を用いて式(3)で表します。

\[w_{std}=w\frac{\sigma_{x}}{\sigma_{y}}　(3)\]

そしてこの標準偏回帰係数が説明変数の影響度を表現しているので、何が最も重要か、あるいは重要でないかといった分析にも使うことができます。

用意した説明変数の影響度分析は色々な場面で活用できそうですね！

多重共線性（マルチコ）への注意

多重共線性（Multicollinearity)とは、重回帰分析に使う説明変数同士で相関係数が高い（相関係数が1や-1に近い）と発生し、予測精度を著しく落とす現象です。

英語でマルチコリニアリティーと呼ぶので、単にマルチコと呼ぶ場合が多いです。

例えば、顧客満足度を目的変数にした重回帰分析をする場合で、以下の図に示すような説明変数を選択したと仮定します。

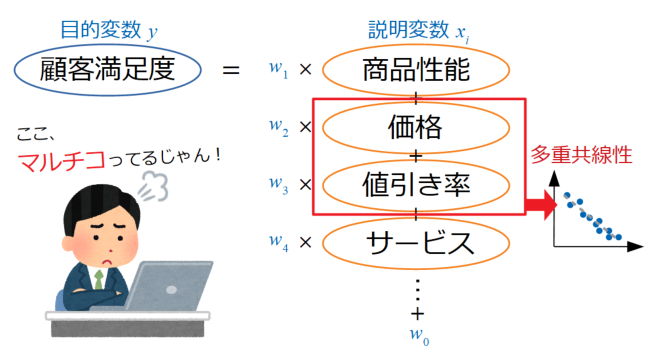
ここで価格と値引き率が選択されていますが、共に商品全体の価格に関する項目なので、もしこの二つの変数の相関が高かったらマルチコになっている可能性が高く、モデルの予測精度を下げてしまいます。

このマルチコこと多重共線性を避けるためには、説明変数間でそれぞれが独立しているかどうかを見極めなければなりません。

多重共線性を完全に排除するのはかなり難しいですが、ここでは2つの調査方法を簡単に紹介しておきます。

多重共線性を回避するためには？

まず、最も手軽に調べる方法として、それぞれの変数間の相関を確認するペアプロットという手法があります。

この方法では散布図を見ることによって（時には相関係数を算出することによって）おおまかに相関の有無を調べることができます。

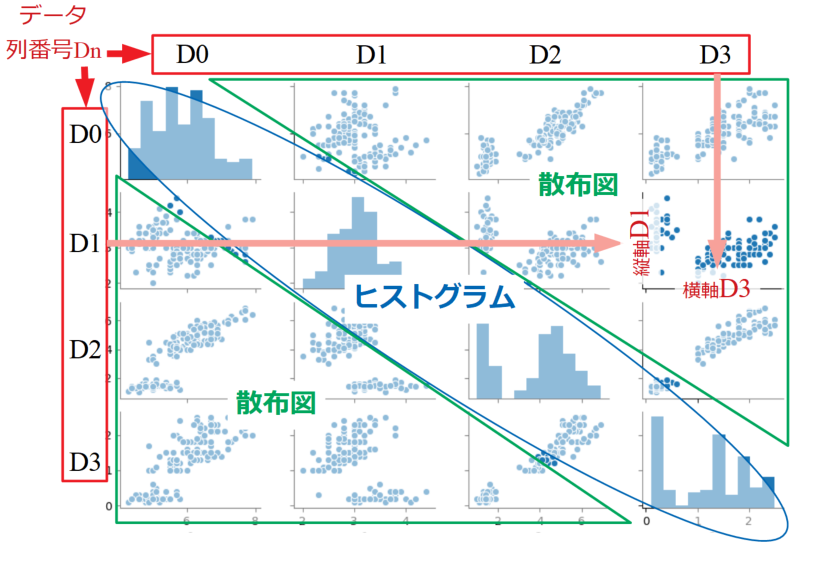
ペアプロットはPythonのseabornというライブラリを使えば簡単に作ることができます。詳しくは「Python/seabornで行列散布図!ペアプロット方法と設定」という記事をご覧ください。

しかしながら、ペアプロットによる見た目や2変数間の相関係数だけを確認していただけでは、多変数間にまたがって間接的に作用する共線性を調べることはできません。

その他の調査方法としてはVIF統計量（VIF：Variance Inflation Factor）が10以上あったら…というような方法もあるようですが、多重共線性の調査はかなり奥が深そうですので、ここでは名前だけをメモしておきます。

理解が深まったら記事にしてみたいですね！

カテゴリカル変数の取扱い：one-hot-encoding

重回帰分析は何も測定データやシミュレーションデータ等の連続性を持ったデータに使うとは限りません。

例えば男性や女性といった性別、国や地名といった出身地もデータとして利用することがあり、このような分類系データのことをカテゴリカル変数と呼びます。

カテゴリカル変数を数値化する場合、順番に0, 1, 2…とナンバリングしてしまうと、機械学習の時にコンピュータは大きい数値と小さい数値を量として認識してしまいます。

実際にはカテゴリカル変数に量的な意味合いはないので、1つの要素を0か1に変換するone-hot-encodingという方法をとります（出来上がった変数をダミー変数と呼ぶとのこと）。

百聞は一見にしかずということで、出身地データを例に説明します。
以下の図は出身地としてそれぞれ東京、大阪、名古屋といった3つのクラスに分類させて並べたものです。このデータをone-hot-encodingするとYというマトリクスを得ます。

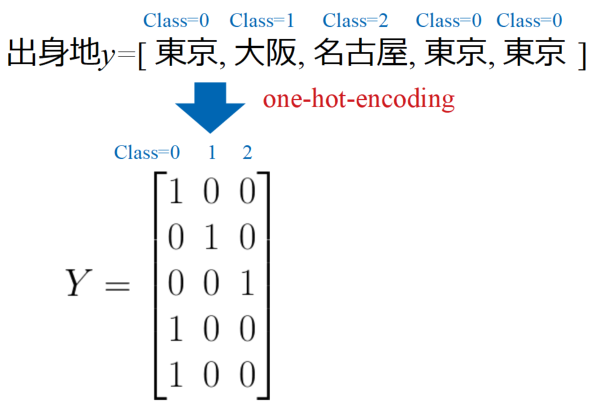
このような行列データとすることで、データの情報を失うことなくカテゴリーを表現することが可能です。

scikit-learnによる重回帰分析のコードの例

前置きは長くなってしまいましたが、これからscikit-learnを使った重回帰分析のサンプルプログラムをPythonで書いていきます。

全コード

以下に全コードを紹介しますが、ほとんど単回帰分析で書いたコードと同じです（エラー回避の.reshapeや回帰の部分はまったく同じ）。

from sklearn import linear_model
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# データを用意する
w0 = 1.0                              # 定数
w1 = -1.4                             # 係数1
w2 = -0.1                             # 係数2
x1 = np.random.uniform(0, 10, 300)    # ノイズを含んだx軸を作成
x2 = np.random.uniform(0, 10, 300)    # ノイズを含んだy軸を作成

# ノイズを含んだ平面点列データを作成
y = w0 + (w1 * x1) + (w2 * x2) + np.random.uniform(0, 5, 300)

# scikit-learnのmodel.fitではデータの次元を明示する必要がある
# reshapeを使って各データを1Dデータと明示する
x1 = x1.reshape(-1, 1)
x2 = x2.reshape(-1, 1)
y = y.reshape(-1, 1)

# 説明変数を1つに結合する
x = np.c_[x1, x2]

# 線形回帰をする
model = linear_model.LinearRegression()    # 線形回帰モデルを定義
model.fit(x, y)                            # 学習実行
reg_y = model.predict(x)                   # xに対する予測値を計算

# パラメータ算出
reg_wn = model.coef_                       # 偏回帰係数
reg_w0 = model.intercept_                  # 切片
r2 = model.score(x, y)                     # 決定係数
print(reg_wn)
print(reg_w0)
print(r2)

# パラメータからモデルを可視化するために3次元データを作成する
X1 = np.arange(0, 11, 2.0)                             # x軸を作成
X2 = np.arange(0, 11, 2.0)                             # y軸を作成
X, Y = np.meshgrid(X1, X2)                             # x軸とy軸からグリッドデータを作成
Z = reg_w0 + (reg_wn[0, 0] * X) + (reg_wn[0, 1] * Y)   # 回帰平面のz値を作成

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# グラフの入れ物を用意する。
fig = plt.figure()
ax1 = Axes3D(fig)

# 軸のラベルを設定する。
ax1.set_xlabel('x1')
ax1.set_ylabel('x2')
ax1.set_zlabel('y')

# データプロットする。
ax1.scatter3D(x1, x2, y, label='Dataset')
ax1.plot_wireframe(X, Y, Z, label='Regression plane')
plt.legend()

# グラフを表示する。
plt.show()
plt.close()

from sklearn import linear_model

import numpy as np

from matplotlib import pyplot as plt

from mpl_toolkits.mplot3d import Axes3D

# データを用意する

w0 = 1.0 # 定数

w1 = -1.4 # 係数1

w2 = -0.1 # 係数2

x1 = np.random.uniform(0, 10, 300) # ノイズを含んだx軸を作成

x2 = np.random.uniform(0, 10, 300) # ノイズを含んだy軸を作成

# ノイズを含んだ平面点列データを作成

y = w0 + (w1 * x1) + (w2 * x2) + np.random.uniform(0, 5, 300)

# scikit-learnのmodel.fitではデータの次元を明示する必要がある

# reshapeを使って各データを1Dデータと明示する

x1 = x1.reshape(-1, 1)

x2 = x2.reshape(-1, 1)

y = y.reshape(-1, 1)

# 説明変数を1つに結合する

x = np.c_[x1, x2]

# 線形回帰をする

model = linear_model.LinearRegression() # 線形回帰モデルを定義

model.fit(x, y) # 学習実行

reg_y = model.predict(x) # xに対する予測値を計算

# パラメータ算出

reg_wn = model.coef_ # 偏回帰係数

reg_w0 = model.intercept_ # 切片

r2 = model.score(x, y) # 決定係数

print(reg_wn)

print(reg_w0)

print(r2)

# パラメータからモデルを可視化するために3次元データを作成する

X1 = np.arange(0, 11, 2.0) # x軸を作成

X2 = np.arange(0, 11, 2.0) # y軸を作成

X, Y = np.meshgrid(X1, X2) # x軸とy軸からグリッドデータを作成

Z = reg_w0 + (reg_wn[0, 0] * X) + (reg_wn[0, 1] * Y) # 回帰平面のz値を作成

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# グラフの入れ物を用意する。

fig = plt.figure()

ax1 = Axes3D(fig)

# 軸のラベルを設定する。

ax1.set_xlabel('x1')

ax1.set_ylabel('x2')

ax1.set_zlabel('y')

# データプロットする。

ax1.scatter3D(x1, x2, y, label='Dataset')

ax1.plot_wireframe(X, Y, Z, label='Regression plane')

plt.legend()

# グラフを表示する。

plt.show()

plt.close()

単回帰分析の時との違いは、「#データを用意する」で係数が増えている所と、「#説明変数を1つにする」の部分で複数ある説明変数をNumpyの関数で結合している所です。

よく発生するエラーについての内容や、回帰部分のコードは「Python機械学習！scikit-learnによる単回帰分析」に詳細を記載しましたので、是非ご確認下さい。

また、重回帰分析から得られたパラメータを使って平面を描画するために、「#パラメータからモデルを可視化するために3次元データを作成する」で3Dデータを作り、3次元プロットしている所が追加されています。

3Dプロットに関しては「Python/matplotlib3Dプロット！面と散布図を作成」に詳細を記載しましたので、必要な方は参考にして下さい。

実はmatplotlibを使った3Dプロットの方法や先に紹介した標準化の記事も、この記事のために書いたものなのでよく内容がマッチしていると思います（たぶん…）。

実行結果

以下はコンソールに表示される実行結果です。
上記コードで設定した平面のパラメータと近い偏回帰係数が得られています。切片はかなり離れている印象を受けますがノイズの含ませ方かも知れません。どれだけフィットしているかを示す決定係数が0.8を超えているので十分フィットしていると言えそうです。

[[-1.38900846 -0.10199737]]    # 偏回帰係数
[3.57053973]                   # 切片
0.8618083359026354             # 決定係数

[[-1.38900846 -0.10199737]] # 偏回帰係数

[3.57053973] # 切片

0.8618083359026354 # 決定係数

サンプルとして作成したデータセットを散布図プロット、回帰平面をメッシュグリッドで面プロットしたものが以下の図です。

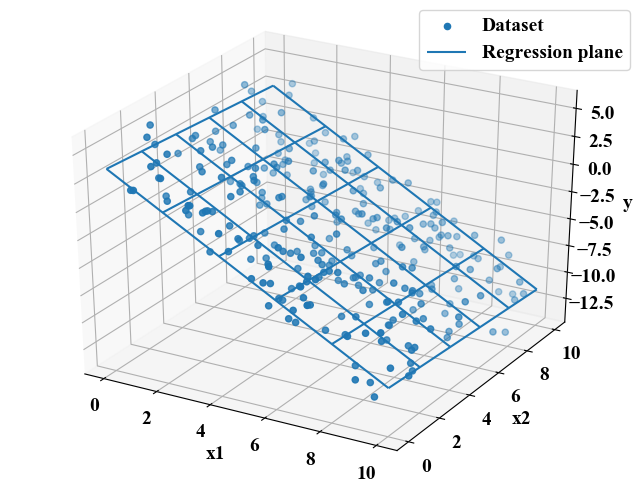
それっぽいことが出来てきたかな？Excelでも回帰分析はできるけど、Pythonでやると綺麗にグラフ化しやすいですね！グラフはぐりぐり回すこともできるので、是非お持ちの環境で体験してみて下さい！

まとめ

本記事では重回帰分析の概要と活用例を式と図付きで説明し、標準偏回帰係数・多重共線性（マルチコ）・カテゴリカル変数について紹介しました。

重回帰分析はデータをよく見なければ正確な分析をすることは難しそうという印象を受けましたが、まずは学習を始めるためのきっかけになる内容にはなったかなと思います。

単回帰・重回帰…1つずつ学習をしていくことでG検定対策にもなっていると思います！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！