PythonのSciPyでハイパスフィルタをかける!

信号の高周波成分のみを抽出したい時はハイパスフィルタを利用します。フィルタ処理は難しい理論がありますが、PythonのSciPyであれば使うだけなら簡単にできます。

こんにちは。wat(@watlablog)です。ローパスフィルタを学んだ後はハイパスフィルタです。ここではハイパスフィルタをPythonでコーディングする方法を習得します！

目次（項目クリックでジャンプできます）

ハイパスフィルタについて

ハイパスフィルタとは？

前回の記事（PythonのSciPyでローパスフィルタをかける！）ではローパスフィルタを学んで高周波帯域のノイズ除去を行いました。

フィルタには様々な種類があり、ハイパスフィルタ(High-pass filter)も使用頻度の高いフィルタです。

ハイパスフィルタとは、信号の高周波成分のみを通過（パス）させ、低周波帯域の成分は阻止（カット）するフィルタのことを指します。

ハイパスフィルタの有名な事例は画像処理におけるエッジ処理です。画像も2次元の信号であるため、波形の信号処理技術はそのまま応用可能です。

画像の輪郭というのは波形でいうと急激に値が変化する部分となり、高周波成分を多く含みます。ハイパスフィルタを使うことでエッジ部分を検出しやすくしたり、シャープネスを強くした画像に変換したりといった処理がよく行われています。

ハイパスフィルタで重要な因子と用語（図解）

ハイパスフィルタは高周波帯域の信号を通し、低周波帯域の信号を阻止するので、周波数軸で考えると下図のように3つの領域（「阻止域」「遷移域」「通過域」）に分けられます。

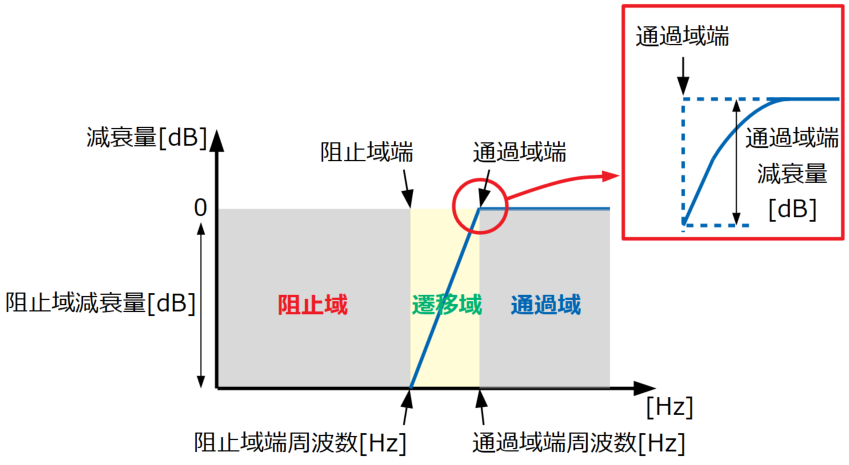
ほとんどローパスフィルタの時の図と同じですね。今回もバターワースフィルタにおける実装例を以下に示していきます。

PythonのSciPyハイパスフィルタ

ソースコード

メインファイル

ソースコードを以下に示します。フィルタ処理を実際に行う部分はdef文を使って関数化しました。関数の使い方については「Pythonの関数def文の使い方！引数や別ファイル式も解説」の記事に詳細を示しています。

まずはメイン(main_filter.py)のコードです。

サンプルとしてガウシアンノイズを生成していますが、こちらについては「Pythonでガウス分布を持つノイズの作り方と調整方法」の記事を参照下さい。

中身ですが、ローパスの時とパラメータは全く同じです。但し、通過域と阻止域の周波数の大小関係が逆になっている点だけに注意して下さい。減衰量の考え方は変更ありません。基本は上に添付した図のイメージを頭に入れておけば問題無いと思います。

import numpy as np
from matplotlib import pyplot as plt
 
samplerate = 25600                                   #波形のサンプリングレート
x = np.arange(0, 12800) / samplerate                 #波形生成のための時間軸の作成
data = np.random.normal(loc=0, scale=1, size=len(x)) #ガウシアンノイズを生成
 
fp = 3000       #通過域端周波数[Hz]
fs = 1500       #阻止域端周波数[Hz]
gpass = 3       #通過域端最大損失[dB]
gstop = 40      #阻止域端最小損失[dB]
 
data_filt = filter_function.highpass(data, samplerate, fp, fs, gpass, gstop)

import numpy as np

from matplotlib import pyplot as plt

samplerate = 25600 #波形のサンプリングレート

x = np.arange(0, 12800) / samplerate #波形生成のための時間軸の作成

data = np.random.normal(loc=0, scale=1, size=len(x)) #ガウシアンノイズを生成

fp = 3000 #通過域端周波数[Hz]

fs = 1500 #阻止域端周波数[Hz]

gpass = 3 #通過域端最大損失[dB]

gstop = 40 #阻止域端最小損失[dB]

data_filt = filter_function.highpass(data, samplerate, fp, fs, gpass, gstop)

関数ファイル

関数ファイル（filter_function.py)もローパスとほぼ同じです。signal.butterでhighを指定する所が変化点です。

正規化の考え方や根拠は「PythonのSciPyでローパスフィルタをかける！」の記事をご覧下さい。

import numpy as np
from scipy import signal
 
#バターワースフィルタ（ハイパス）
def highpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "high")           #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y                                      #フィルタ後の信号を返す

import numpy as np

from scipy import signal

#バターワースフィルタ（ハイパス）

def highpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "high") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y #フィルタ後の信号を返す

参考：フーリエ変換まで含めた全コード

先ほどまではフィルタ処理の部分のみを解説していましたが、ファイルを2つ作ったり面倒だと思いますので、コピペしてすぐ動かせる全コードを以下に示します。

このコードはサンプル波形を生成して、フーリエ変換とデシベル変換を行っており、フィルタ前後の波形を比較する事が可能です。是非動かして遊んでみて下さい。

import numpy as np
from scipy import signal
from scipy import fftpack
from matplotlib import pyplot as plt

#バターワースフィルタ（ハイパス）
def highpass(x, samplerate, fp, fs, gpass, gstop):
    fn = samplerate / 2                           #ナイキスト周波数
    wp = fp / fn                                  #ナイキスト周波数で通過域端周波数を正規化
    ws = fs / fn                                  #ナイキスト周波数で阻止域端周波数を正規化
    N, Wn = signal.buttord(wp, ws, gpass, gstop)  #オーダーとバターワースの正規化周波数を計算
    b, a = signal.butter(N, Wn, "high")           #フィルタ伝達関数の分子と分母を計算
    y = signal.filtfilt(b, a, x)                  #信号に対してフィルタをかける
    return y                                      #フィルタ後の信号を返す

# オーバーラップ処理
def ov(data, samplerate, Fs, overlap):
    Ts = len(data) / samplerate                                                # 全データ長
    Fc = Fs / samplerate                                                       # フレーム周期
    x_ol = Fs * (1 - (overlap / 100))                                          # オーバーラップ時のフレームずらし幅
    N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100))))  # 抽出するフレーム数（平均化に使うデータ個数）

    array = []                                                                 # 抽出したデータを入れる空配列の定義

    # forループでデータを抽出
    for i in range(N_ave):
        ps = int(x_ol * i)                                                     # 切り出し位置をループ毎に更新
        array.append(data[ps:ps + Fs:1])                                       # 切り出し位置psからフレームサイズ分抽出して配列に追加
    return array, N_ave                                                        # オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする

# 窓関数処理（ハニング窓）
def hanning(data_array, Fs, N_ave):
    han = signal.hann(Fs)                    # ハニング窓作成
    acf = 1 / (sum(han) / Fs)                # 振幅補正係数(Amplitude Correction Factor)

    # オーバーラップされた複数時間波形全てに窓関数をかける
    for i in range(N_ave):
        data_array[i] = data_array[i] * han  # 窓関数をかける

    return data_array, acf

# FFT処理
def fft_ave(data_array, samplerate, Fs, N_ave, acf):
    fft_array = []
    for i in range(N_ave):
        fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2)))  # FFTをして配列に追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。

    fft_axis = np.linspace(0, samplerate, Fs)                                  # 周波数軸を作成
    fft_array = np.array(fft_array)                                            # 型をndarrayに変換
    fft_mean = np.mean(fft_array, axis=0)                                      # 全てのFFT波形の平均を計算

    return fft_array, fft_mean, fft_axis

#リニア値からdBへ変換
def db(x, dBref):
    y = 20 * np.log10(x / dBref)     #変換式
    return y                         #dB値を返す

# ここからサンプル波形生成とフィルタ処理をする-------------------------------------------
samplerate = 25600
x = np.arange(0, 12800) / samplerate                    # 波形生成のための時間軸の作成
data = np.random.normal(loc=0, scale=1, size=len(x))    # ガウシアンノイズを生成

fp = 3000                                               # 通過域端周波数[Hz]
fs = 1500                                               # 阻止域端周波数[Hz]
gpass = 3                                               # 通過域端最大損失[dB]
gstop = 40                                              # 阻止域端最小損失[dB]

# ハイパスをかける関数を実行
data_filt = highpass(data, samplerate, fp, fs, gpass, gstop)
# ------------------------------------------------------------------------------

# ここから平均化フーリエ変換とデシベル変換を行う----------------------------------------------
Fs = 4096                                               # フレームサイズ
overlap = 90                                            # オーバーラップ率

# 作成した関数を実行：オーバーラップ抽出された時間波形配列
t_array_org, N_ave_org = ov(data, samplerate, Fs, overlap)
t_array_filt, N_ave_filt = ov(data_filt, samplerate, Fs, overlap)

# 作成した関数を実行：ハニング窓関数をかける
t_array_org, acf_org = hanning(t_array_org, Fs, N_ave_org)
t_array_filt, acf_filt = hanning(t_array_filt, Fs, N_ave_filt)

# 作成した関数を実行：FFTをかける
fft_array_org, fft_mean_org, fft_axis_org = fft_ave(t_array_org, samplerate, Fs, N_ave_org, acf_org)
fft_array_filt, fft_mean_filt, fft_axis_filt = fft_ave(t_array_filt, samplerate, Fs, N_ave_filt, acf_filt)

# dB変換する
fft_mean_org = db(fft_mean_org, 2e-5)
fft_mean_filt = db(fft_mean_filt, 2e-5)
# -----------------------------------------------------------------------------------

# ここからグラフ描画---------------------------------------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')
ax2 = fig.add_subplot(212)
ax2.yaxis.set_ticks_position('both')
ax2.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('SP[Pa]')
ax2.set_xlabel('Frequency [Hz]')
ax2.set_ylabel('SPL[dB]')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
ax1.plot(x, data, label='original', lw=1)
ax1.plot(x, data_filt, label='filtered', lw=1)
ax2.plot(fft_axis_org, fft_mean_org, label='original', lw=1)
ax2.plot(fft_axis_filt, fft_mean_filt, label='filtered', lw=1)
plt.legend()

# 軸のリミットを設定する。
ax2.set_xlim(0, max(fft_axis_org)/2)
ax2.set_ylim(-20, 100)

# レイアウト設定
fig.tight_layout()

# グラフを表示する。
plt.show()
plt.close()
# -----------------------------------------------------------------------------------

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

import numpy as np

from scipy import signal

from scipy import fftpack

from matplotlib import pyplot as plt

#バターワースフィルタ（ハイパス）

def highpass(x, samplerate, fp, fs, gpass, gstop):

fn = samplerate / 2 #ナイキスト周波数

wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化

ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化

N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算

b, a = signal.butter(N, Wn, "high") #フィルタ伝達関数の分子と分母を計算

y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける

return y #フィルタ後の信号を返す

# オーバーラップ処理

def ov(data, samplerate, Fs, overlap):

Ts = len(data) / samplerate # 全データ長

Fc = Fs / samplerate # フレーム周期

x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅

N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数（平均化に使うデータ個数）

array = [] # 抽出したデータを入れる空配列の定義

# forループでデータを抽出

for i in range(N_ave):

ps = int(x_ol * i) # 切り出し位置をループ毎に更新

array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加

return array, N_ave # オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする

# 窓関数処理（ハニング窓）

def hanning(data_array, Fs, N_ave):

han = signal.hann(Fs) # ハニング窓作成

acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor)

# オーバーラップされた複数時間波形全てに窓関数をかける

for i in range(N_ave):

data_array[i] = data_array[i] * han # 窓関数をかける

return data_array, acf

# FFT処理

def fft_ave(data_array, samplerate, Fs, N_ave, acf):

fft_array = []

for i in range(N_ave):

fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))) # FFTをして配列に追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。

fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成

fft_array = np.array(fft_array) # 型をndarrayに変換

fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算

return fft_array, fft_mean, fft_axis

#リニア値からdBへ変換

def db(x, dBref):

y = 20 * np.log10(x / dBref) #変換式

return y #dB値を返す

# ここからサンプル波形生成とフィルタ処理をする-------------------------------------------

samplerate = 25600

x = np.arange(0, 12800) / samplerate # 波形生成のための時間軸の作成

data = np.random.normal(loc=0, scale=1, size=len(x)) # ガウシアンノイズを生成

fp = 3000 # 通過域端周波数[Hz]

fs = 1500 # 阻止域端周波数[Hz]

gpass = 3 # 通過域端最大損失[dB]

gstop = 40 # 阻止域端最小損失[dB]

# ハイパスをかける関数を実行

data_filt = highpass(data, samplerate, fp, fs, gpass, gstop)

# ------------------------------------------------------------------------------

# ここから平均化フーリエ変換とデシベル変換を行う----------------------------------------------

Fs = 4096 # フレームサイズ

overlap = 90 # オーバーラップ率

# 作成した関数を実行：オーバーラップ抽出された時間波形配列

t_array_org, N_ave_org = ov(data, samplerate, Fs, overlap)

t_array_filt, N_ave_filt = ov(data_filt, samplerate, Fs, overlap)

# 作成した関数を実行：ハニング窓関数をかける

t_array_org, acf_org = hanning(t_array_org, Fs, N_ave_org)

t_array_filt, acf_filt = hanning(t_array_filt, Fs, N_ave_filt)

# 作成した関数を実行：FFTをかける

fft_array_org, fft_mean_org, fft_axis_org = fft_ave(t_array_org, samplerate, Fs, N_ave_org, acf_org)

fft_array_filt, fft_mean_filt, fft_axis_filt = fft_ave(t_array_filt, samplerate, Fs, N_ave_filt, acf_filt)

# dB変換する

fft_mean_org = db(fft_mean_org, 2e-5)

fft_mean_filt = db(fft_mean_filt, 2e-5)

# -----------------------------------------------------------------------------------

# ここからグラフ描画---------------------------------------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(211)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = fig.add_subplot(212)

ax2.yaxis.set_ticks_position('both')

ax2.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('SP[Pa]')

ax2.set_xlabel('Frequency [Hz]')

ax2.set_ylabel('SPL[dB]')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

ax1.plot(x, data, label='original', lw=1)

ax1.plot(x, data_filt, label='filtered', lw=1)

ax2.plot(fft_axis_org, fft_mean_org, label='original', lw=1)

ax2.plot(fft_axis_filt, fft_mean_filt, label='filtered', lw=1)

plt.legend()

# 軸のリミットを設定する。

ax2.set_xlim(0, max(fft_axis_org)/2)

ax2.set_ylim(-20, 100)

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

# -----------------------------------------------------------------------------------

実行結果

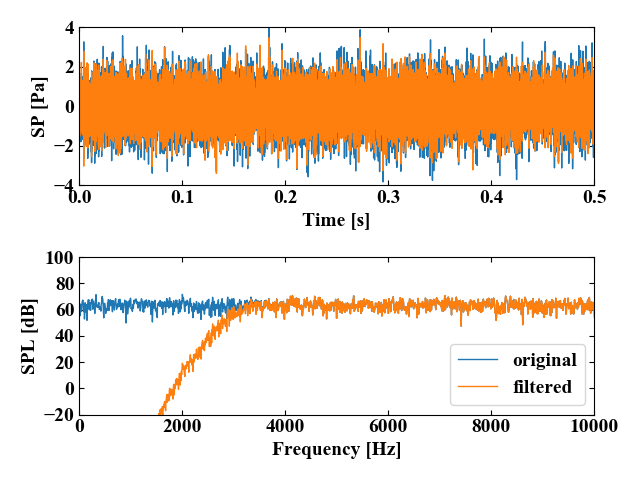
ハイパスフィルタをガウシアンノイズに対してかけた結果です。
下図上段が時間波形、下段が上段の波形をFFTした後の周波数波形です。それぞれフィルタ前（original）とフィルタ後（filtered）を比較しています。

ここではFFTやデシベル変換も使っていますが、それぞれの詳細は以下の記事にまとめていますので、是非ご覧ください。

PythonでFFT！SciPyのFFTまとめ
 Pythonで音圧のデシベル(dB)変換式と逆変換式

ローパスの時と同じように、ノイズ波形だけではつまらないので、サイン波を二つ合成させた波形を作って効果を確認していきます。

上のメインコード（main_filter.py）の波形生成部分とフィルタ周波数を以下のように変更してみます。

data = np.sin(2.0 * np.pi * 50 * x) + np.sin(2.0 * np.pi * 500 * x)  #サイン波を合成

fp = 400       #通過域端周波数[Hz]
fs = 200       #阻止域端周波数[Hz]
gpass = 3      #通過域端最大損失[dB]
gstop = 40     #阻止域端最小損失[dB]

data = np.sin(2.0 * np.pi * 50 * x) + np.sin(2.0 * np.pi * 500 * x) #サイン波を合成

fp = 400 #通過域端周波数[Hz]

fs = 200 #阻止域端周波数[Hz]

gpass = 3 #通過域端最大損失[dB]

gstop = 40 #阻止域端最小損失[dB]

元波形は500[Hz]のサイン波に50[Hz]のサイン波が重畳されているため、500[Hz]のサイン波全体がうねり成分を持っています。今回はハイパスフィルタを使うことでこのうねり成分を除去してみました。これも一種のノイズ除去ですね。

まとめ

フィルタ処理の一種であるハイパスフィルタをPythonで使えるようになりました。

ハイパスフィルタもローパスフィルタと同じように通過域、遷移域、阻止域を持ちますが、その位置関係に違いがありました。

SciPyを使えば簡単にこれらのフィルタ設計ができることを学びました。

ローパスを学んだ後だとハイパスは一瞬で理解できたぞ！フィルタを自由に使いこなすのは信号処理技術者としての基礎だと思うので、しっかり復習しよう！

Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

ハイパスフィルタについて

ハイパスフィルタとは？

ハイパスフィルタで重要な因子と用語（図解）

PythonのSciPyハイパスフィルタ

ソースコード

メインファイル

関数ファイル

参考：フーリエ変換まで含めた全コード

実行結果

まとめ

コメント

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

ハイパスフィルタについて

ハイパスフィルタとは？

ハイパスフィルタで重要な因子と用語（図解）

PythonのSciPyハイパスフィルタ

ソースコード

メインファイル

関数ファイル

参考：フーリエ変換まで含めた全コード

実行結果

まとめ

SNSでもご購読できます。

コメント

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル