2019.04.17

PythonでFFTをする前にオーバーラップ処理をしよう!

一定の長さで計測した時間波形をFFT（高速フーリエ変換）する時、周波数波形の「平均化」という処理を行う時があります。その際に前処理として必要になるオーバーラップ処理の方法を説明します。

こんにちは。wat(@watlablog)です。
信号処理の基本にFFTがありますが、より精度の良い分析のためには「平均化処理」をすることがあります。
ここではその際に必要となるオーバーラップ処理について説明します。

目次（項目クリックでジャンプできます）

オーバーラップ処理を使いこなそう！

FFT分析のフロー

FFT（高速フーリエ変換）は大変便利な波形分析手法ですが、データの周期性を仮定している等、いくつかの使用上の注意点があります。

実際の分析はある有限長のデータフレーム単位で行う必要があります。そしてデータの整形上、前回窓関数を自作した時説明したように、窓関数をかけてFFTのための前処理を行うことがあります。

最も一般的に行われているFFT分析のフローは以下の図に示す通りです。
※ここでは一定の振動データを長時間測定した場合についてのフローを説明しています。

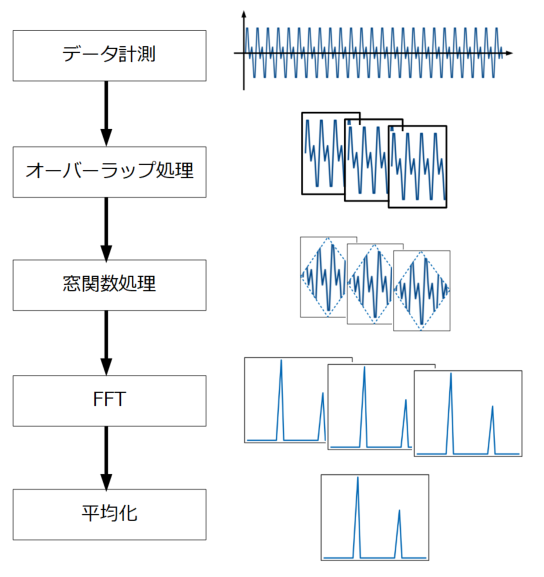
計測したデータはある程度の時間長を持ちますが、実際のデータは理想通り毎回同じ波形が繰り返し出てはくれません。

実際の現象は必ずばらつきを含むので、通常、定常振動のFFT分析は長時間データを任意フレームに多数分割し、その分割したそれぞれのフレームに窓関数をかけ、FFTを行い、最後に平均化処理をすることで統計的に周波数分析を行います。

ここで、多数のフレームに分割する部分に「オーバーラップ処理」と呼ばれる手法を用います。

オーバーラップ処理とは（図解）？

平均化したFFT分析をするために、計測したデータを多数のフレームに分割する作業が必要になります。

以下の図のように単純にフレームを横にずらしてデータフレームを作っていく作業が最も基本的な分割の方法です。

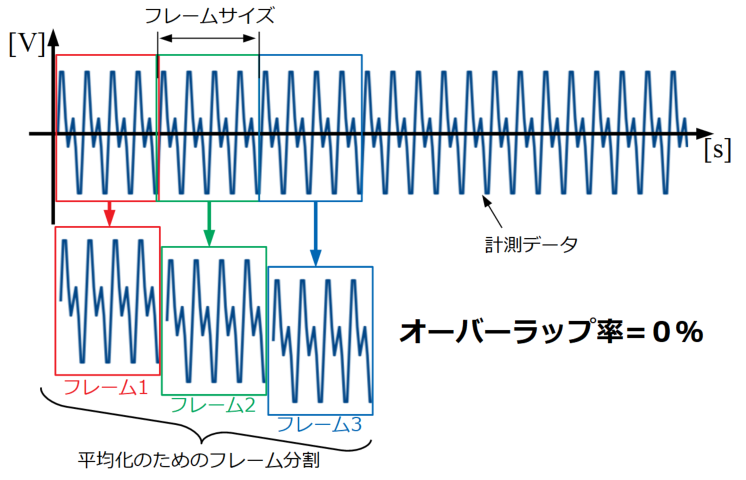
ここで、フレームはある一定の横幅（フレームサイズ）をもっています。上図のようにフレーム1、フレーム2...とそれぞれのフレームがラップしないようにデータを抽出する場合、オーバーラップ率は0%と表現します。

オーバーラップ率を上げていくとこのフレームが重なり合ってきます。

以下の図はオーバーラップ率50％の場合の例です。

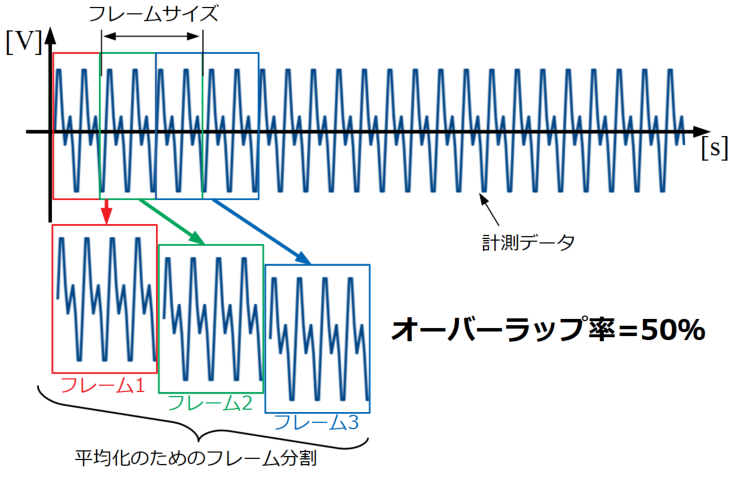
オーバーラップ率が50％の場合、各フレームは丁度フレームサイズの半分の位置で重なり合います。

これだけの説明だとなぜこんな処理が必要なのか疑問に思う方もいると思いますが、オーバーラップの使用には重要な理由があります。

オーバーラップを使う理由（図解）

オーバーラップを必要とする理由は、窓関数にあります。一定の振動を測定した場合はハニング窓やハミング窓等、フレームの両端をなめらかに0にする窓関数をかけます。

上で説明したオーバーラップ0％と50％を例にとって再度説明すると、以下の図のように比較することが可能です。

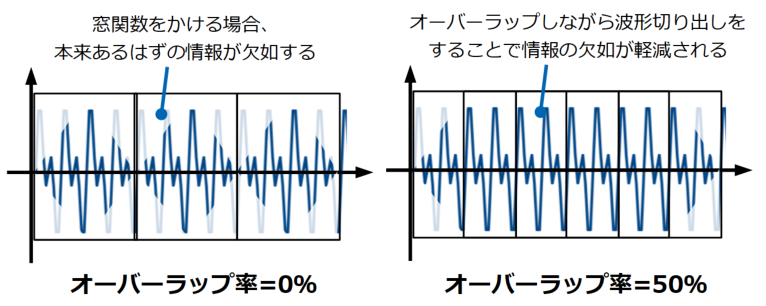
オーバーラップしてデータを抽出した波形に対して窓関数をかけるわけですが、オーバーラップ率が0％の場合は左の図のようにフレームの両端がなめらかに0になります。

ということはここに物理的に重要な振動が周期的に出ていた場合、窓関数によってその情報を欠損させてしまうことになります。

しかしながら、オーバーラップ率を大きくして右の図のようにデータを抽出すると、窓関数で減衰しない部分がずれていくので、全フレームで見れば情報の欠如は軽減されます。

精度の良いFFTのために窓関数を使いたいけど、情報は失いたくない、そんな理由でオーバーラップ手法は活用されます。

オーバーラップってよくばりな手法だね！

オーバーラップをコーディングしよう！

計算式

オーバーラップの実装に必要な計算はデータ数やフレームサイズ、どれくらいラップするかを決めれば一意に決まります。

以下の図が計算に使用する変数です。フレームサイズがデータポイント数なのに対し、フレーム周期はフレームサイズを時間にしたものです（フレームサイズに時間刻み幅をかければ良い）。

オーバーラップ位置$x_{ol}$は「最初のフレームから何ポイント目に次のフレームが来るか」を意味しています。

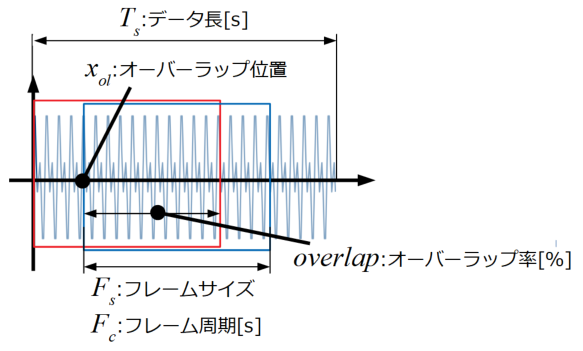
関係式は以下の通りです。

$$ x_{ol}= F_{s}\left ( 1-\frac{overlap}{100} \right ) $$

$$ N_{ave}= \frac{T_{s}-\left ( F_{c} \frac{overlap}{100}\right )}{F_{c}\left ( 1-\frac{overlap}{100} \right )} $$

コードと実行例

まずオーバーラップ部分を関数で作成したコードを紹介します。

オーバーラップして切り出したデータは空配列arrayにfor文で追加していきます。この関数は波形データdata、サンプリングレートsamplerate[Hz]、フレームサイズFs, オーバーラップ率overlap[%]を引数として、オーバーラップされた波形の配列データarray、平均化回数（＝分割数）N_aveを戻り値として返しています。

import numpy as np
from matplotlib import pyplot as plt

#オーバーラップの関数
def ov(data, samplerate, Fs, overlap):
    Ts = len(data) / samplerate
    Fc = Fs / samplerate
    x_ol = Fs * (1 - (overlap/100))
    N_ave = int((Ts - (Fc * (overlap/100))) / (Fc * (1-(overlap/100))))

    array = []

    for i in range(N_ave):
        ps = int(x_ol * i)
        array.append(data[ps:ps+Fs:1])
    return array, N_ave

import numpy as np

from matplotlib import pyplot as plt

#オーバーラップの関数

def ov(data, samplerate, Fs, overlap):

Ts = len(data) / samplerate

Fc = Fs / samplerate

x_ol = Fs * (1 - (overlap/100))

N_ave = int((Ts - (Fc * (overlap/100))) / (Fc * (1-(overlap/100))))

array = []

for i in range(N_ave):

ps = int(x_ol * i)

array.append(data[ps:ps+Fs:1])

return array, N_ave

続いて、こちらがメインの実行文です。今回は上の関数部分とメインの部分は同じファイルで書いていますので、続けて記述すれば動作するはずです。

サンプルデータは100Hzのサイン波にランダムノイズを重畳させたものを作成しています。

グラフ描画部分にもfor文を使ってオーバーラップされたデータを一つずつ抽出して重ね書きプロットしています。

#メイン
samplerate = 25600
x = np.arange(0, 12800)/samplerate
data = np.sin(2.0 * np.pi * 100 * x) + 0.2 * np.random.randn(len(x)) #サイン波にランダム成分を重畳

Fs = 4096
overlap = 50

data_ol, N_ave = ov(data, samplerate, Fs, overlap)
print(N_ave)
t = np.arange(0, Fs)/samplerate

# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
f = plt.figure()
ax = f.add_subplot(111)
ax.yaxis.set_ticks_position('both')
ax.xaxis.set_ticks_position('both')

#データの範囲と刻み目盛を明示する。
plt.xticks(np.arange(0, 1, 0.1))
plt.yticks(np.arange(-3, 3, 1))
plt.xlim(0,0.2)
plt.ylim(-2, 2)

# 軸のラベルを設定する。
plt.xlabel('Time [s]')
plt.ylabel('Signal [V]')

# データのラベルと線の太さ、凡例の設置を行う。
for j in range(N_ave):
    plt.plot(t, data_ol[j], label='Ch.1', lw=1)

# グラフを表示する。
plt.show()
plt.close()

#メイン

samplerate = 25600

x = np.arange(0, 12800)/samplerate

data = np.sin(2.0 * np.pi * 100 * x) + 0.2 * np.random.randn(len(x)) #サイン波にランダム成分を重畳

Fs = 4096

overlap = 50

data_ol, N_ave = ov(data, samplerate, Fs, overlap)

print(N_ave)

t = np.arange(0, Fs)/samplerate

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

f = plt.figure()

ax = f.add_subplot(111)

ax.yaxis.set_ticks_position('both')

ax.xaxis.set_ticks_position('both')

#データの範囲と刻み目盛を明示する。

plt.xticks(np.arange(0, 1, 0.1))

plt.yticks(np.arange(-3, 3, 1))

plt.xlim(0,0.2)

plt.ylim(-2, 2)

# 軸のラベルを設定する。

plt.xlabel('Time [s]')

plt.ylabel('Signal [V]')

# データのラベルと線の太さ、凡例の設置を行う。

for j in range(N_ave):

plt.plot(t, data_ol[j], label='Ch.1', lw=1)

# グラフを表示する。

plt.show()

plt.close()

ちなみに、元波形はこちら。この波形をオーバーラップをかけながら分割していきます。

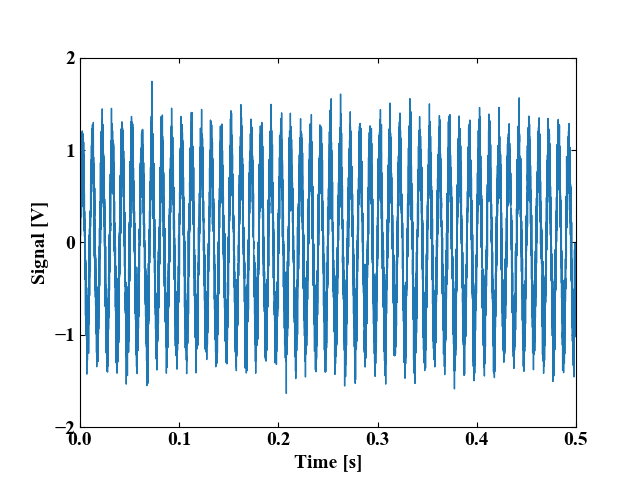
オーバーラップ率＝50％の場合

こちらがオーバーラップ率＝50%の実行結果です。このグラフ内に5個の波形が重ね書きされています。フレームサイズが4096、データ長12800と切りの良い数値なので、50％の場合は波形の位相ずれはありません。

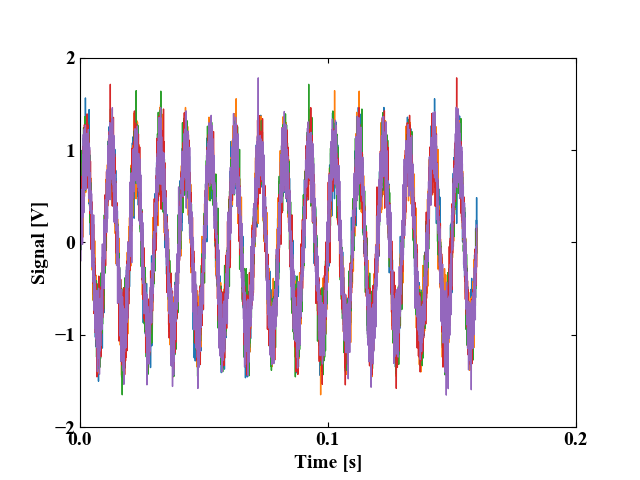
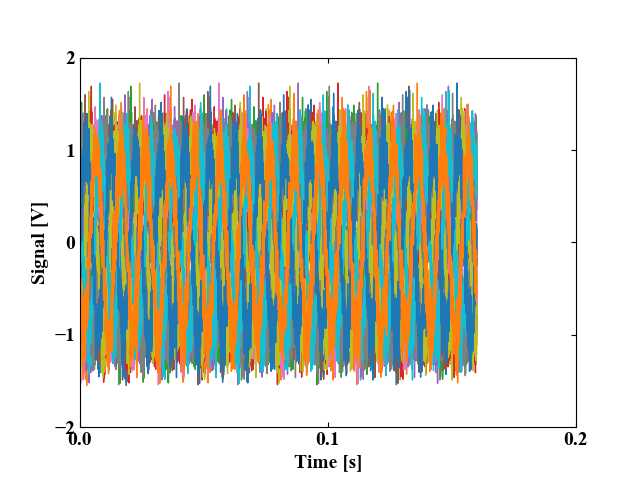
オーバーラップ率＝90％の場合

続いてこちらがオーバーラップ率90%の実行結果です。90％の場合はこのグラフ内に22個の波形が重ね書きされています。オーバーラップ率を増加させていくとデータの数が増えていきます。

この率だと、波形の位相ずれもはっきりとわかりますね。

まとめ

少しボリュームの大きい記事になりましたが、今回は時間波形の分割方法に使われる手法として、オーバーラップを学びました。

オーバーラップを使うと窓関数で欠如される情報を救うことができるため、非常に有用な信号処理方法であると言えます。

だいぶ信号処理に慣れてきたぞ！時間波形の取り扱いなら色々応用ができるようになってきた！

Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

wat

機械工学を専攻し大学院を修了後、技術系の職に就き日々実験やシミュレーションを使う仕事をしています。このブログでは初心者が科学技術プログラムを作れるようになることを目標に、学習結果を記録していきます。著書「いきなりプログラミングPython（翔泳社）」 ※資格・計算力学技術者 1級 2級 (振動) ・計算力学技術者 2級 (熱流体) ・基本情報技術者・G検定・AI実装検定 S級 A級 ※Information ・Amazonのアソシエイトとして、当メディアは適格販売により収入を得ています。・当メディアはGoogleによるユーザーに合わせた自動広告が表示されます。

珈琲より:

2020年1月15日 12:07 AM

はじめまして，珈琲と申します．
FFTの補正やオーバーラップについて学んでいるときにこのサイトに辿り着きました．
要点がまとめられていて大変勉強になります．

質問なのですが，もしオーバーラップ０％で処理を行う場合があったときはHann窓はかけないほうがいいのでしょうか？上記の記載だと０％でHann窓をかけた際は，データの欠損が発生すると思ったのですが，どうなのでしょうか？

よろしくおねがいします．

返信
1. wat より:
  
  2020年1月15日 6:52 PM
  
  ご訪問ありがとうございます！
  参考にして頂き恐縮です。ご質問に対して回答致します。
  
  一般的にはハニング窓は書けた方が良いと言われています。
  FFTは周期関数を前提としているので、複雑な波形を計算しようとするとフレームの最初と最後が不連続になってしまうことが多くあります（位相0の理想波形ではそれほど目立たないかも）。
  窓関数をかけないとFFT波形にこのことが原因で発生するリーケージエラーと呼ばれる誤差要因が入ってきます。
  （FFT波形が見た目にも汚くなる）
  
  オーバーラップをかけなくても、振動成分が安定していればハニングをかけて振幅補正すれば問題ありません。
  補正については「窓関数使用時の補正！FFTの時に忘れがちな計算とは？」を参考にしてみて下さい。
  
  実測波形のように複雑な波形を1フレームだけとってFFTする場合は、いくらかの振動成分が欠如してしまうことが避けられないと思いますので、その場合は通常長時間の測定を行い、オーバーラップをかけながら平均化を行うという処理をします。
  
  …僕自身も勉強中なので正確に伝えられるか不安ですが、もし記事の内容等でご不明点ございましたら、今後もコメントやTwitterでご連絡頂ければと思います！
  
  返信
フーリエ学習中より:

2020年10月12日 4:15 PM

N_aveについての質問です。
データ長÷（フレーム長×（1-オーバーラップ率））＋１ではダメなのでしょうか？

返信
1. wat より:
  
  2020年10月14日 9:13 PM
  
  ご訪問ありがとうございます。
  オーバーラップの計算はこちらの方で幾何学的に値を考えていったため、もしかしたらここに記載の方法ではあまり効率の良い式では無いかも知れません。
  
  pythonで書くと、
  N_ave = int(len(data) / ((Fs * (1 – (overlap / 100))) + 1))
  のような形でしょうか？
  
  もちろん各オーバーラップ率に対応してきっちり抜き出して来れればダメではありません。
  
  ただこちらのデータで、フレームサイズ4096、データ長220160、オーバーラップ率90%の条件で上記式を試した所、最終フレームが3892と端数になってしまいました。
  （もしかして記載した式にミスがあるかも…）
  そちらではオーバーラップを90％等にしても正常に抽出できますか？
  
  返信
  1. ゼロークより:
    
    2021年4月22日 4:25 PM
    
    1年以上前なのでコメントする必要は無さそうですが、自信無さそうな文章が気になったので補足させて頂きます。
    watさんの以下URLで合っています。
    https://watlab-blog.com/2019/04/17/python-overlap/
    
    最初の導入式が無くていきなり答えが来ているから分からない人がいるだけで、上記URLの図の説明に則ればαをオーパーラップ率(%に対して100を割った0.0-1.0の範囲とする)とすると
    Fc * ( 1 – α ) * ( Nave – 1 ) + Fc ≦ Ts
    を満たすMax(Nave)を求めれば良いので、上記URLで説明している式になります。
    
    簡単に以下の条件で考えます。
    　・サンプリング周波数：1Hz(つまり周期1秒)
    　・データ点数：16点
    　・FFTフレーム点数：8点
    　・オーバーラップ率75%(=3/4、つまり、8 * 3/4 = 6点は前フレームと被る)
    
    ナイキスト周波数0.5Hzの周波数分解能が0.125Hzの解析って何が分かるの？というのは置いておきます。
    手で絵を描けばすぐに分かりますが答えは5回となります。
    
    下式に前述した条件を当てはめると、8回になるので計算が合いません。
    データ長÷（フレーム長×（1-オーバーラップ率））
    
    返信
    1. wat より:
      
      2021年4月22日 11:56 PM
      
      ゼローク様、こちらにも補足説明ありがとうございます。
      自分で図を描きながら検証したのですが、うまい説明ができませんでした。
      コメント欄で補足いただくと他の方への説明にもなり、感謝します。
      
      返信

PythonでFFTをする前にオーバーラップ処理をしよう!