運動方程式を手計算で構築するのは大変です。自動的に式を導出することができれば、複雑なモデルでも手計算で間違う可能性が減ります。ここではsympy.physics.mechanicsでラグランジュ法を使った運動方程式の自動導出方法とシミュレーション方法を紹介します。
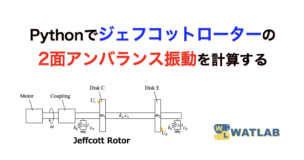
続きを読むPython/SymPy：ラグランジュ法による運動方程式の自動導出
数値解析
Pythonでジェフコットローターの2面アンバランス振動を計算する
回転機の振動問題はアンバランスの修正を目的に検討される場合が多いですが、振動を毎回実験で評価するのは時間がかかって大変です。ここでは実機がなくても簡単に回転機の振動検討ができるよう、Jeffcott Rotorの問題をPythonで解析してみます。アンバランスでよく検討される2面のモデルに対応しているので、是非参考にしてください。
続きを読むPythonでルジャンドル多項式を使ってガウス積分をする方法
数値解析の分野ではガウス積分という求積手法がよく用いられます。ガウス積分はルジャンドル多項式を使って積分点と重みを算出しますが、初学者はまずこれらの概念を理解するのが難しいです。この記事では簡単な関数を題材にガウス積分を計算する方法をPythonコードと共に紹介します。
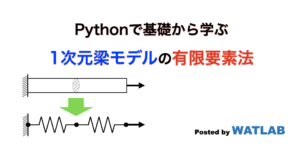
続きを読むPythonで基礎から学ぶ1次元梁モデルの有限要素法
有限要素法は一般的に商用ソフトやオープンソースのライブラリを活用して「使う」ことが多いものですが、理解するためには自分でプログラミングするのが一番です。ここでは手計算でもできるレベルの問題をPythonによる有限要素法コードで解くことで、計算の流れを把握することを目指します。
続きを読むWindowsのWSL2でPython3/GetFEMを使ってみた
計算力学技術者試験の勉強のため、Pythonで使える有限要素法ライブラリGetFEMを使ってみました。GetFEMは通常Linux環境が必要ですが、WindowsでもWSLを使えばLinux環境を手にいれることができます。ここではWindows機でGetFEMを使う時のメモを紹介します。
続きを読む回転機のアンバランス振動をシミュレートするPythonコード
工業製品である回転機はアンバランスを修正することで精密な回転を実現しています。しかし、アンバランスを真に0にすることは難しく、不釣り合い振動の影響をシミュレーションすることは重要です。ここではPythonのscipy.odeintを使ってアンバランス振動を解析する方法を紹介します。
続きを読むPythonで多自由度振動系の過渡応答計算をする時はSciPyを使おう
このブログではしばらく自前のルンゲ・クッタ法を使って振動解析を行ってきました。しかしPythonで常微分方程式の数値計算をする時はSciPyのodeintを使った方が良いです。ここでは巨人の肩に乗るつもりでSciPy/odeintで振動問題を解くための例題を紹介します。
続きを読むPythonで非線形ばねを持つ1自由度振動系の周波数応答関数を求める
振動系の運動方程式において復元力項が非線形になった時、その周波数応答関数は特徴的な形を示します。この記事では非線形ばねを有する1自由度の運動方程式を題材に、ハードニング特性やソフトニング特性の周波数応答関数をPythonで解析する方法を紹介します。
続きを読むPythonで2D移流拡散方程式を数値計算して拡散流れを表現する
これまで当ブログでは2Dの「移流方程式」と「拡散方程式」を扱いました。ここではこれら2つの流体現象を組み合わせた「移流拡散方程式」を学びます。いつも通りPythonでコーディングしながら解説を行い、流れを確認して理解を深めます。
続きを読むPythonで2次元拡散方程式を数値解析して定常解析と比較する
数値流体力学の学習は各要素毎に離散化手法と解析手法を学ぶことが重要です。ここでは2次元の拡散方程式の概要や離散化手法を説明し、Pythonで実装しながら学習します。結果は定常解析の結果と比較することでラプラス方程式にも触れてみます。
続きを読む12