2019.05.20

Pythonでピアノ音楽のスペクトログラムを作ってみた

時系列データのSTFT（短時間フーリエ変換）からスペクトログラム表示させる方法を学びました。ここでは活用例としてピアノ音楽のスペクトログラムを作り、画像保存する所までを紹介します。

こんにちは。wat(@watlablog)です。
本記事は作ったコードで色々遊んでみる回です。ピアノ音楽をスペクトログラムで画像的に眺めてみましょう！

目次（項目クリックでジャンプできます）

STFTとスペクトログラムのおさらい

計算の概要

色々な計算結果を眺めてみる前に、そもそもどんな計算をしているかをおさらいしておきましょう。

今回はピアノで録音した音声ファイル（.wav）をPythonで読み、時系列データをフレームでオーバーラップ分割しながら順次FFTをかけていきます。

この計算をSTFT（短時間フーリエ変換）と呼び、結果を時間×周波数×振幅レベルで表示させたものをスペクトログラム表示と呼びます。図解は以下です。

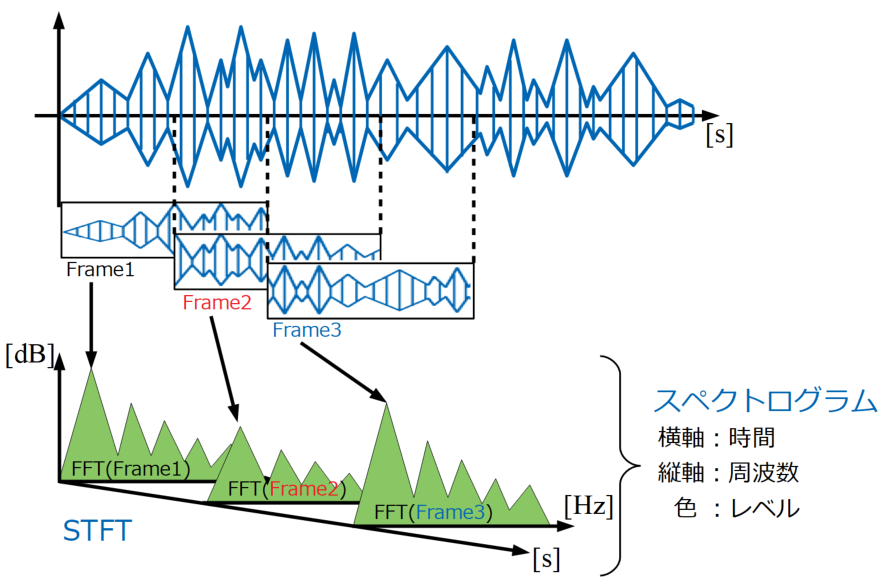
さらに詳しい説明と、段階を追ったコードの説明は「Pythonで音のSTFT計算を自作！スペクトログラム表示する方法」に全て書きましたので、そちらを参照下さい。

Pythonコード全文

wavファイルを読み込んでSTFT計算を行い、結果をスペクトログラム表示するPythonプログラムコードを以下に示します。

プログラムは可読性を考慮して関数ファイルとメインファイルに.pyを分けました。メインファイルでimport functionを宣言してから、メインファイルの方を実行することで同じ結果を得ることができると思います。

wav読み込み時のfilenameは実際に存在するwavファイルの名前を付けて下さい。

関数ファイル（function.py）

import numpy as np
from scipy import signal
from scipy import fftpack
import soundfile as sf

def wavload(path):
    data, samplerate = sf.read(path)
    return data, samplerate

# オーバーラップ処理
def ov(data, samplerate, Fs, overlap):
    Ts = len(data) / samplerate                     # 全データ長
    Fc = Fs / samplerate                            # フレーム周期
    x_ol = Fs * (1 - (overlap / 100))               # オーバーラップ時のフレームずらし幅
    N_ave = int((Ts - (Fc * (overlap / 100))) /\
                (Fc * (1 - (overlap / 100))))       # 抽出するフレーム数（平均化に使うデータ個数）

    array = []                                      # 抽出したデータを入れる空配列の定義

    # forループでデータを抽出
    for i in range(N_ave):
        ps = int(x_ol * i)                          # 切り出し位置をループ毎に更新
        array.append(data[ps:ps + Fs:1])            # 切り出し位置psからフレームサイズ分抽出して配列に追加
        final_time = (ps + Fs)/samplerate           #切り出したデータの最終時刻
    return array, N_ave, final_time                 # オーバーラップ抽出されたデータ配列とデータ個数、最終時間を戻り値にする


# 窓関数処理（ハニング窓）
def hanning(data_array, Fs, N_ave):
    han = signal.hann(Fs)                           # ハニング窓作成
    acf = 1 / (sum(han) / Fs)                       # 振幅補正係数(Amplitude Correction Factor)

    # オーバーラップされた複数時間波形全てに窓関数をかける
    for i in range(N_ave):
        data_array[i] = data_array[i] * han         # 窓関数をかける

    return data_array, acf


# FFT処理
def fft_ave(data_array, samplerate, Fs, N_ave, acf):
    fft_array = []
    fft_axis = np.linspace(0, samplerate, Fs)      # 周波数軸を作成
    a_scale = aweightings(fft_axis)                # 聴感補正曲線を計算

    # FFTをして配列にdBで追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。
    for i in range(N_ave):
        fft_array.append(db\
                        (acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))\
                        , 2e-5))

    fft_array = np.array(fft_array) + a_scale      # 型をndarrayに変換し、A特性をかける
    fft_mean = np.mean(fft_array, axis=0)          # 全てのFFT波形の平均を計算

    return fft_array, fft_mean, fft_axis

# リニア値からdBへ変換
def db(x, dBref):
    y = 20 * np.log10(x / dBref)                   # 変換式
    return y                                       # dB値を返す

# dB値からリニア値へ変換
def idb(x, dBref):
    y = dBref * np.power(10, x / 20)  # 変換式
    return y  # リニア値を返す

#聴感補正（A特性カーブ）
def aweightings(f):
    if f[0] == 0:
        f[0] = 1
    else:
        pass
    ra = (np.power(12194, 2) * np.power(f, 4)) / \
         ((np.power(f, 2) + np.power(20.6, 2)) * \
          np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * \
                  (np.power(f, 2) + np.power(737.9, 2))) * \
          (np.power(f, 2) + np.power(12194, 2)))
    a = 20 * np.log10(ra) + 2.00
    return a

import numpy as np

from scipy import signal

from scipy import fftpack

import soundfile as sf

def wavload(path):

data, samplerate = sf.read(path)

return data, samplerate

# オーバーラップ処理

def ov(data, samplerate, Fs, overlap):

Ts = len(data) / samplerate # 全データ長

Fc = Fs / samplerate # フレーム周期

x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅

N_ave = int((Ts - (Fc * (overlap / 100))) /\

(Fc * (1 - (overlap / 100)))) # 抽出するフレーム数（平均化に使うデータ個数）

array = [] # 抽出したデータを入れる空配列の定義

# forループでデータを抽出

for i in range(N_ave):

ps = int(x_ol * i) # 切り出し位置をループ毎に更新

array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加

final_time = (ps + Fs)/samplerate #切り出したデータの最終時刻

return array, N_ave, final_time # オーバーラップ抽出されたデータ配列とデータ個数、最終時間を戻り値にする

# 窓関数処理（ハニング窓）

def hanning(data_array, Fs, N_ave):

han = signal.hann(Fs) # ハニング窓作成

acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor)

# オーバーラップされた複数時間波形全てに窓関数をかける

for i in range(N_ave):

data_array[i] = data_array[i] * han # 窓関数をかける

return data_array, acf

# FFT処理

def fft_ave(data_array, samplerate, Fs, N_ave, acf):

fft_array = []

fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成

a_scale = aweightings(fft_axis) # 聴感補正曲線を計算

# FFTをして配列にdBで追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。

for i in range(N_ave):

fft_array.append(db\

(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))\

, 2e-5))

fft_array = np.array(fft_array) + a_scale # 型をndarrayに変換し、A特性をかける

fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算

return fft_array, fft_mean, fft_axis

# リニア値からdBへ変換

def db(x, dBref):

y = 20 * np.log10(x / dBref) # 変換式

return y # dB値を返す

# dB値からリニア値へ変換

def idb(x, dBref):

y = dBref * np.power(10, x / 20) # 変換式

return y # リニア値を返す

#聴感補正（A特性カーブ）

def aweightings(f):

if f[0] == 0:

f[0] = 1

else:

pass

ra = (np.power(12194, 2) * np.power(f, 4)) / \

((np.power(f, 2) + np.power(20.6, 2)) * \

np.sqrt((np.power(f, 2) + np.power(107.7, 2)) * \

(np.power(f, 2) + np.power(737.9, 2))) * \

(np.power(f, 2) + np.power(12194, 2)))

a = 20 * np.log10(ra) + 2.00

return a

メインファイル(main.py）

import function
import numpy as np
from matplotlib import pyplot as plt

path = 'filename.wav'                       #ファイルパスを指定
data, samplerate = function.wavload(path)   #wavファイルを読み込む
x = np.arange(0, len(data)) / samplerate    #波形生成のための時間軸の作成

# Fsとoverlapでスペクトログラムの分解能を調整する。
Fs = 4096                                   # フレームサイズ
overlap = 75                                # オーバーラップ率

# オーバーラップ抽出された時間波形配列
time_array, N_ave, final_time = function.ov(data, samplerate, Fs, overlap)

# ハニング窓関数をかける
time_array, acf = function.hanning(time_array, Fs, N_ave)

# FFTをかける
fft_array, fft_mean, fft_axis = function.fft_ave(time_array, samplerate, Fs, N_ave, acf)

# スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置
fft_array = fft_array.T

# ここからグラフ描画
# グラフをオブジェクト指向で作成する。
fig = plt.figure()
ax1 = fig.add_subplot(111)

# データをプロットする。
im = ax1.imshow(fft_array, \
                vmin = -10, vmax = 60,
                extent = [0, final_time, 0, samplerate], \
                aspect = 'auto',\
                cmap = 'jet')

# カラーバーを設定する。
cbar = fig.colorbar(im)
cbar.set_label('SPL [dBA]')

# 軸設定する。
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Frequency [Hz]')

# スケールの設定をする。
ax1.set_xticks(np.arange(0, 120, 2))
ax1.set_yticks(np.arange(0, 20000, 1000))
ax1.set_xlim(0, 14)
ax1.set_ylim(0, 4000)

# グラフを表示する。
plt.show()
plt.close()

import function

import numpy as np

from matplotlib import pyplot as plt

path = 'filename.wav' #ファイルパスを指定

data, samplerate = function.wavload(path) #wavファイルを読み込む

x = np.arange(0, len(data)) / samplerate #波形生成のための時間軸の作成

# Fsとoverlapでスペクトログラムの分解能を調整する。

Fs = 4096 # フレームサイズ

overlap = 75 # オーバーラップ率

# オーバーラップ抽出された時間波形配列

time_array, N_ave, final_time = function.ov(data, samplerate, Fs, overlap)

# ハニング窓関数をかける

time_array, acf = function.hanning(time_array, Fs, N_ave)

# FFTをかける

fft_array, fft_mean, fft_axis = function.fft_ave(time_array, samplerate, Fs, N_ave, acf)

# スペクトログラムで縦軸周波数、横軸時間にするためにデータを転置

fft_array = fft_array.T

# ここからグラフ描画

# グラフをオブジェクト指向で作成する。

fig = plt.figure()

ax1 = fig.add_subplot(111)

# データをプロットする。

im = ax1.imshow(fft_array, \

vmin = -10, vmax = 60,

extent = [0, final_time, 0, samplerate], \

aspect = 'auto',\

cmap = 'jet')

# カラーバーを設定する。

cbar = fig.colorbar(im)

cbar.set_label('SPL [dBA]')

# 軸設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('Frequency [Hz]')

# スケールの設定をする。

ax1.set_xticks(np.arange(0, 120, 2))

ax1.set_yticks(np.arange(0, 20000, 1000))

ax1.set_xlim(0, 14)

ax1.set_ylim(0, 4000)

# グラフを表示する。

plt.show()

plt.close()

ピアノ楽曲とスペクトログラム

スケール（音階）

スケールは日本語で音階を意味します。今回はCスケール、ハ長調で単にドレミファソラシドと昇って、その後ドシラソファミレドと降りてくるように弾きました。

音声はこちら。※メディアプレーヤークリックで音が出ます。

スペクトログラムはこちら。

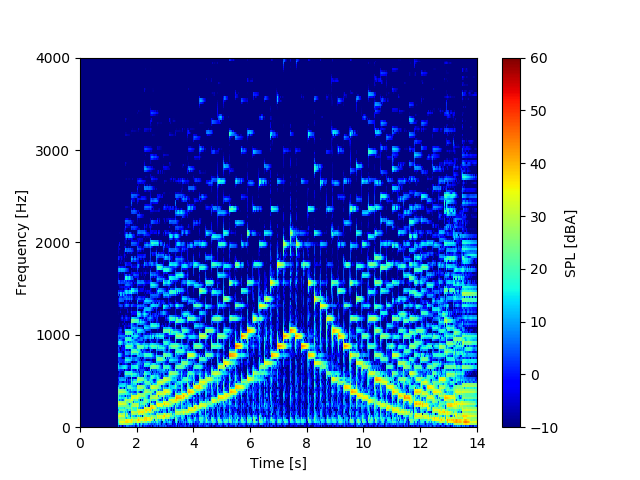
キレイに左右対称の図となっていますね。やはりピアノは1音1音がはっきりしているので、スペクトログラムにすると1つ1つがインパルス的な波形になっていることが読み取れます。

グリッサンド

グリッサンドとはスケールと同じようなものですが、指滑らせながら連続的に鍵盤を弾く奏法です。慣れないと痛いです。

音声はこちら。※メディアプレーヤークリックで音が出ます。

スペクトログラムはこちら。

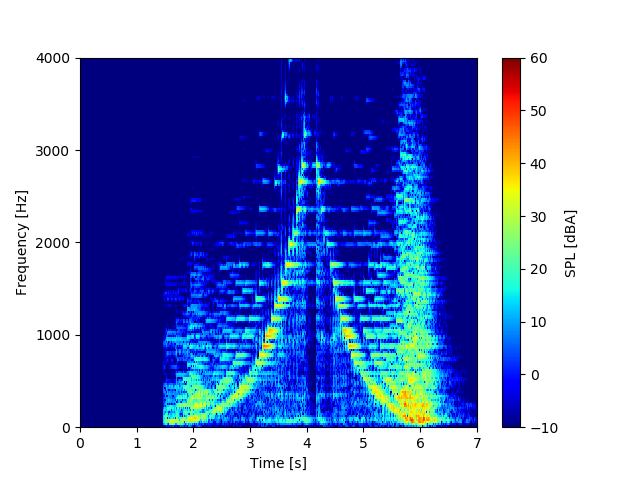
スケールに比べて、高調波成分があまり無いですね。1音1音垂直に指で打鍵していないのが原因？電子ピアノなのであまりその辺の再現度はなさそうですが。

猫ふんじゃった

「猫ふんじゃった」はみんななぜか弾ける超有名な曲です。

曲はこんな感じ。※メディアプレーヤークリックで音が出ます。

スペクトログラムはこちら。

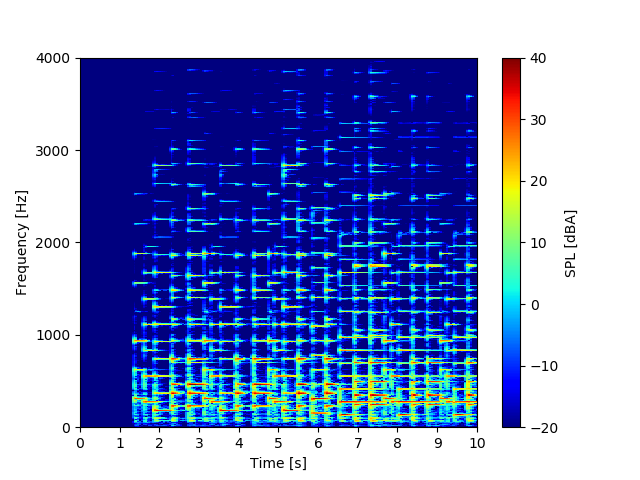
色々な音を弾くと、横を向いた十字架が至る所にあるという感じでもはやわけがわかりませんね…！

ショパン：幻想即興曲

ショパンの幻想即興曲も有名ですね。僕が弾いたものでも、多分聴けばわかるかと。

音声はこんな感じ。※メディアプレーヤークリックで音が出ます。

スペクトログラムはこちら。

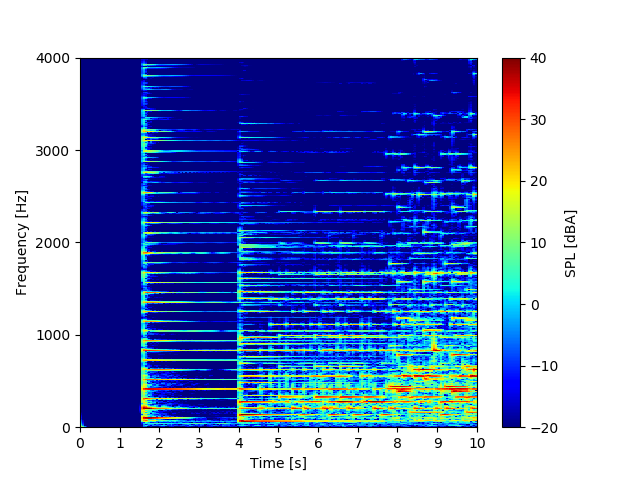
最初の「じゃーん」の部分はG#のオクターブなので500Hz弱の所が最も強く出ていることがわかりますね。左手だけのアルペジオ部分から右手の主旋律が加わる部分も何となく層がわかる感じ。

ショパン：スケルツォ第2番

ショパンのスケルツォ第2番はあまり知っている人がいないかも知れませんね。個人的に好きな曲なのでよく弾いています（雑ですが）。

音声はこんな感じ。※メディアプレーヤークリックで音が出ます。

スペクトログラムはこちら。

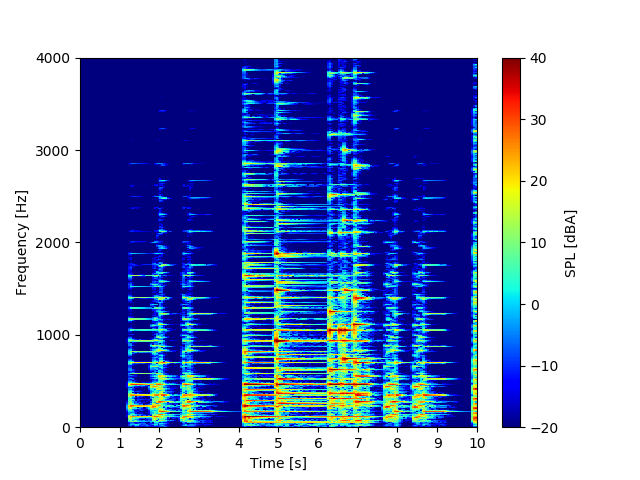
この曲、冒頭部分はピアノ弾きの間で「ところてん」と呼ばれています。音のリズムを「んートコロテン♪トコロテン♪…にっぽ↑ーん、文化国家！」と歌詞を付けると丁度良くはまるんです。今回はその部分を解析してみました。

スペクトログラムの画像を保存する方法

matplotlibでスペクトログラムを作成していますが、このカラーマップの図は特に画像ファイルとして保存したくなる時があります。

音声データの解析結果を画像ファイルとして保存してあれば、後に機械学習用のデータとしても使えます。

軸を消して画像として保存

機械学習を念頭に置くために、保存する画像からはカラーバー、目盛線を含む軸を全て消して保存します。

上のメインファイルからグラフ描画部分を以下のコードに変更するだけで完了です。

# ここからグラフ描画
# グラフをオブジェクト指向で作成する。
fig = plt.figure()
ax1 = fig.add_subplot(111)

# データをプロットする。
im = ax1.imshow(fft_array, \
                vmin = -10, vmax = 60,
                extent = [0, final_time, 0, samplerate], \
                aspect = 'auto',\
                cmap = 'jet')

# スケールの設定をする。
ax1.set_xticks(np.arange(0, 120, 2))
ax1.set_yticks(np.arange(0, 20000, 1000))
ax1.set_xlim(0, 14)
ax1.set_ylim(0, 4000)

# 軸を消す設定
ax1.tick_params(labelbottom = False, bottom = False)
ax1.tick_params(labelleft = False, left = False)

# 画像を保存する
plt.savefig('fig.png', bbox_inches = 'tight')

# グラフを表示する。
plt.show()
plt.close()

# ここからグラフ描画

# グラフをオブジェクト指向で作成する。

fig = plt.figure()

ax1 = fig.add_subplot(111)

# データをプロットする。

im = ax1.imshow(fft_array, \

vmin = -10, vmax = 60,

extent = [0, final_time, 0, samplerate], \

aspect = 'auto',\

cmap = 'jet')

# スケールの設定をする。

ax1.set_xticks(np.arange(0, 120, 2))

ax1.set_yticks(np.arange(0, 20000, 1000))

ax1.set_xlim(0, 14)

ax1.set_ylim(0, 4000)

# 軸を消す設定

ax1.tick_params(labelbottom = False, bottom = False)

ax1.tick_params(labelleft = False, left = False)

# 画像を保存する

plt.savefig('fig.png', bbox_inches = 'tight')

# グラフを表示する。

plt.show()

plt.close()

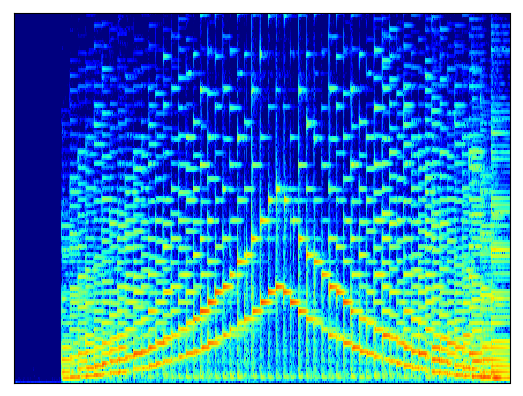
実行すると「fig.png」という画像が保存されます。ここまで覚えれば、後は色々な活用方法が考えられますね。

まとめ

本ページではSTFT計算とスペクトログラム表示のおさらいを行い、様々なピアノ音楽のスペクトログラムを観察しました。

また、スペクトログラムを画像として保存することで機械学習への使い道考えました。

今回は「やってみた」系の遊び記事ですが、作ったコードは使ってなんぼ！色々遊んで技術の幅を拡げよう！

Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

wat

機械工学を専攻し大学院を修了後、技術系の職に就き日々実験やシミュレーションを使う仕事をしています。このブログでは初心者が科学技術プログラムを作れるようになることを目標に、学習結果を記録していきます。著書「いきなりプログラミングPython（翔泳社）」 ※資格・計算力学技術者 1級 2級 (振動) ・計算力学技術者 2級 (熱流体) ・基本情報技術者・G検定・AI実装検定 S級 A級 ※Information ・Amazonのアソシエイトとして、当メディアは適格販売により収入を得ています。・当メディアはGoogleによるユーザーに合わせた自動広告が表示されます。

harrods227 より:

2020年1月8日 10:30 PM

とても参考になりました。
フォルダ内にあるwavファイルをスペクトログラム画像に一括変換するにはどうすれば良いのでしょうか？　ご教授いただけると嬉しいです。
よろしくお願い致します。

返信
1. wat より:
  
  2020年1月9日 6:44 AM
  
  ご訪問ありがとうございます！
  僕の方も丁度その内容のプログラムが欲しかったので、「Pythonでフォルダ内全wavをスペクトログラムに変換してみた」という記事に記載してみました。
  この内容で回答になりますでしょうか？
  もしご不明点やその他要望がございましたら、再度コメントで教えて頂けると助かります！
  
  返信
  1. harrods227 より:
    
    2020年1月9日 8:52 PM
    
    はい、とても適切な回答でした。まさにやりたかった内容です。
    ご対応ありがとうございました。
    よろしくお願い致します。
    
    返信
    1. wat より:
      
      2020年1月11日 7:31 AM
      
      ご返信ありがとうございます。
      解決できたようでよかったです！
      
      返信
harrods227 より:

2020年9月14日 12:59 PM

お久しぶりです。
お元気ですか？
またご教授頂きたい事があります。
スペクトログラムの最大音圧の時の周波数と音圧を数値で得るにはどうすればいいですか？
また、音圧の大きい順に5つまでの周波数と音圧を数値で知ることも可能ですか？
以上、よろしくお願い致します。

返信
1. wat より:
  
  2020年9月20日 5:42 PM
  
  お久しぶりです。回答遅れて申し訳ございません。
  スペクトログラムといっても、2Dの配列なので最大値と周波数を取得することは可能です。
  配列の最大値を得るにはnp.max(fft_array)、最大値の位置を得るにはnp.argmax(fft_array)とします。
  
  但し、2D配列に対してnp.argmax(fft_array)を使うと平坦化された指標が得られる（4096✖️2の配列だったらサイズが1Dで8192になる）ので、divmod（）等を使ってフレームサイズで割った余りに対して周波数分解能をかけると、周波数[Hz]の数値が得られると思います。
  
  「大きい順に5つまでの」を実現するためには、一度2D配列をソートしてから抽出するという手が考えられます。
  しかし、この方法だと分解能によっては最大値付近の点が複数抽出されるだけになりそうです。
  やりたいことが「大きい値が全体のどこに分布しているか」を調べることだとすると、もしかして想定通り動作しない可能性があります。
  
  FFT波形からピーク値をもってくるには、別途「ピーク検出アルゴリズム」を使うのが常套手段と思います。
  面白そうなので当ブログでもやってみようと思いますが、これには少し時間がかかりそうです。
  
  もし書きかけのコードがございましたらコメントやTwitterでもお気軽に相談下さい。
  よろしくお願い致します。
  
  返信
2. wat より:
  
  2020年9月30日 12:00 AM
  
  既に解決されているかも知れませんが、こちらでもご質問を頂いた後にスペクトログラムからのピーク検出アルゴリズムを検討してみました。
  「Pythonでスペクトログラムからピーク値を任意数抽出する方法」に説明を書いてみました。
  ただこちらで考えたものなので、もしかするともっと効率の良い一般的なアルゴリズムがどこかにあるかも知れません（もしそのようなリンクを探していたら教えて頂けると助かります…）。
  
  返信
kazunori より:

2021年7月5日 3:39 PM

初めてコメントさせていただきます。
現在、機械学習の勉強をしている大学生です。
音を学習して、エンジンの回転数を推定する回帰モデルを作りたいと思っております。
例えば、ドレミファソラシドを学習させて１オクターブ上げた音を聞かせたとき
１オクターブ上のドレミファソラシドを推定するといったイメージです。
難しいのは、一つの音でこちらのページのように複数の周波数の音圧が立っていることです。
単純に決定木などで回帰モデルを作ろうと思ったのですが、学習させたパラメータ以外の重みが０となってしまうので、分類しかできないです。（学習させた周波数のみが入力変数となってしまうという意味です。）
もしお勧めの手法等ご存じでしたらご教示いただけますと嬉しいです。

返信
1. wat より:
  
  2021年7月10日 5:09 AM
  
  ご訪問ありがとうございます。
  おそらく実機の音は様々な外乱を含むため、かなり難しい問題であると存じます。
  まだ当ブログでも画像や音の学習はやっていませんが、
  スペクトログラムのような画像データ、時間波形のような音声データをそのまま学習させると、測定された背景ノイズがちょっと異なるだけで汎化性能が落ちるのではと懸念されます。
  
  例えば、エンジンの回転数はピアノのドレミのような離散的な音階ではなく、連続的にスイープアップしたりスイープダウンしますが、
  回転次数は基本周波数(回転1次周波数)の等倍で発生するはずです。
  そこに実車であればその他の部品の次数が多数立つと思いますが、
  いきなり機械学習モデルにデータを投入するのではなく、まずは物理的に解釈可能な、分析したい回転次数という特徴量をいかに作り出すかが重要なのではと思いました。
  そうすれば決定木やサポートベクターマシンの分類器でもある程度の性能がでるのでは…と思います。
  （回転次数毎の振幅というベクトルを学習させる？…あくまで感想ですみません）
  
  ノイズを削ぐところで分類型の機械学習を使って、回転数予測事に回帰するのも面白いかも知れません。
  
  面白そうなテーマでしたので長文になってしまいました。
  こちらであまり経験がないので、思いついた事の感想となり、明確な手法のご提案はできなく申し訳ございません。
  
  もしかしたら当ブログの信号処理カテゴリのフィルタ処理、ピーク検出処理、ケプストラム分析（周波数波形のノイズフロアと変動成分の分離）…あたりがノイズ分離等の参考になるかも知れません。
  
  返信
yuusuke より:

2021年12月4日 1:58 PM

初めまして　コメント失礼いたします。
音響信号処理の勉強をしている大学生です。
ピアノの音色について勉強しており、音色解析のために
貴殿の音源データをお借りしたいのですがよろしいでしょうか。
何卒よろしくお願いします。

返信
1. wat より:
  
  2021年12月4日 2:31 PM
  
  ご訪問ありがとうございます。
  このブログの素材は特に自由に使って頂いて構いません。
  是非ご活用ください。
  
  返信
  1. yuusuke より:
    
    2021年12月4日 2:34 PM
    
    ご返信ありがとうございます。
    それでは音源ファイルを活用させていただきます。
    
    返信

Pythonでピアノ音楽のスペクトログラムを作ってみた

STFTとスペクトログラムのおさらい

計算の概要

Pythonコード全文

関数ファイル（function.py）

メインファイル(main.py）

ピアノ楽曲とスペクトログラム

スケール（音階）

グリッサンド

猫ふんじゃった

ショパン：幻想即興曲

ショパン：スケルツォ第2番

スペクトログラムの画像を保存する方法

軸を消して画像として保存

まとめ

コメント

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

STFTとスペクトログラムのおさらい

計算の概要

Pythonコード全文

関数ファイル（function.py）

メインファイル(main.py）

ピアノ楽曲とスペクトログラム

スケール（音階）

グリッサンド

猫ふんじゃった

ショパン：幻想即興曲

ショパン：スケルツォ第2番

スペクトログラムの画像を保存する方法

軸を消して画像として保存

まとめ

SNSでもご購読できます。

コメント

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル