
フーリエ変換は様々な分野で使われている分析手法です。しかし計測時の制約から周波数分解能が足りずに正確な振幅を得られない場合もあります。この記事では、少ない情報でもフーリエ変換時の周波数分解能を高める方法を考察します。
こんにちは。wat(@watlablog)です。ここでは、フーリエ変換時の周波数分解能をなんとか高められないか悪あがきをしてみます!
フーリエ変換時の周波数分解能について
フーリエ変換についておさらい(Pythonコード)
フーリエ変換について、まだ使った事が無い方は、是非当WATLABブログの「PythonでFFT実装!SciPyのフーリエ変換まとめ」という記事をご覧下さい。
この記事ではフーリエ変換の特徴や簡単なFFTコード、窓関数やオーバーラップを使ったPythonコード、様々な関数の周波数分析結果、周波数軸での鏡像現象や応用までまとめていますので、多分これからフーリエ変換を学ぶ人にとって参考になると思います。
周波数分解能\(df\)はフレーム周期で決まる
まずフーリエ変換を行った時の周波数分解能について見てみましょう。
以下のコードで3つの正弦波信号のフーリエ変換を計算してみます。ここでそれぞれの信号は振幅と振動数は全て同じですが、波形の全時間長(秒数)のみが異なります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt # フーリエ変換をする関数 def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成 return spectrum, amp, phase, freq # 様々な時間長の時間波形を生成 samplerate = 25600 x1 = np.arange(0, 128000)/samplerate data1 = np.sin(2 * np.pi * 1 * x1) x2 = np.arange(0, 51200)/samplerate data2 = np.sin(2 * np.pi * 1 * x2) x3 = np.arange(0, 25600)/samplerate data3 = np.sin(2 * np.pi * 1 * x3) # フーリエ変換をそれぞれ実行 spectrum1, amp1, phase1, freq1 = calc_fft(data1, samplerate) spectrum2, amp2, phase2, freq2 = calc_fft(data2, samplerate) spectrum3, amp3, phase3, freq3 = calc_fft(data3, samplerate) # 各信号で情報をプリント print('df1=',np.round(freq1[1], 2), '[Hz]', 'T1=', len(data1) * (1/samplerate), '[s]', '1/T=', 1/(len(data1) * (1/samplerate)), '[Hz]') print('df2=',np.round(freq2[1], 2), '[Hz]', 'T2=', len(data2) * (1/samplerate), '[s]', '1/T=', 1/(len(data2) * (1/samplerate)), '[Hz]') print('df3=',np.round(freq3[1], 2), '[Hz]', 'T3=', len(data3) * (1/samplerate), '[s]', '1/T=', 1/(len(data3) * (1/samplerate)), '[Hz]') # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Amplitude') # スケールの設定をする。 ax2.set_xticks(np.arange(0, 5, 0.5)) ax2.set_xlim(0, 3) ax2.set_yticks(np.arange(0, 10, 0.2)) ax2.set_ylim(0, 1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x1, data1, label='data1', lw=1) ax1.plot(x2, data2, label='data2', lw=1) ax1.plot(x3, data3, label='data3', lw=1) ax2.plot(freq1, amp1, label='data1', lw=1, marker='o') ax2.plot(freq2, amp2, label='data2', lw=1, marker='o') ax2.plot(freq3, amp3, label='data3', lw=1, marker='o') # レイアウト設定 fig.tight_layout() plt.legend() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
上記コードを実行すると以下の結果を得ます。
まずはprintで出力している文章ですが、それぞれの信号の実際の周波数分解能\(df\)、実際のフレーム周期\(T\)、フレーム周期の逆数から計算した周波数\(1/T\)を示しています。
|
1 2 3 |
df1= 0.2 [Hz] T1= 5.0 [s] 1/T= 0.2 [Hz] df2= 0.5 [Hz] T2= 2.0 [s] 1/T= 0.5 [Hz] df3= 1.0 [Hz] T3= 1.0 [s] 1/T= 1.0 [Hz] |
図を用いて説明すると以下のグラフになります。つまり、周波数分解能はフーリエ変換した時のフレーム周期の逆数で求める事が出来るという事を言っています。
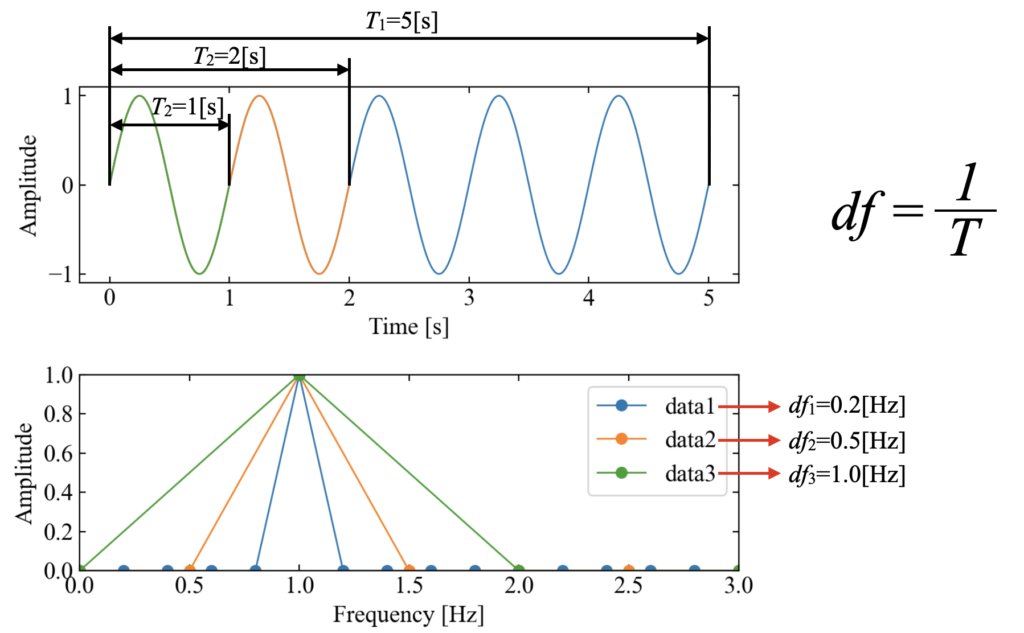
フレーム周期はサンプリング周波数、データ点数で決まります。どういった条件で計測したかどうかがわかれば、FFTしなくても周波数分解能は計算可能です。
周波数分析する時には\(df\)を常に気にすべき
以下の図は先ほどのPythonコードで0.5[Hz]の正弦波をフーリエ変換した結果ですが、十分な時間長を持ったenough dataと、enough dataに比べ時間長が乏しいpoor dataを比較した結果です。
フーリエ変換した振幅成分を見てみると、poor dataは周波数分解能\(df\)=0.2[Hz]であるため0.5[Hz]にピークを持つ真の信号の特徴を正確に見積もれていない事がわかります。
enough dataはフレーム周期が100[s]であるため、\(df\)=0.01[Hz]と0.5[Hz]のピークを十分解像出来ています。
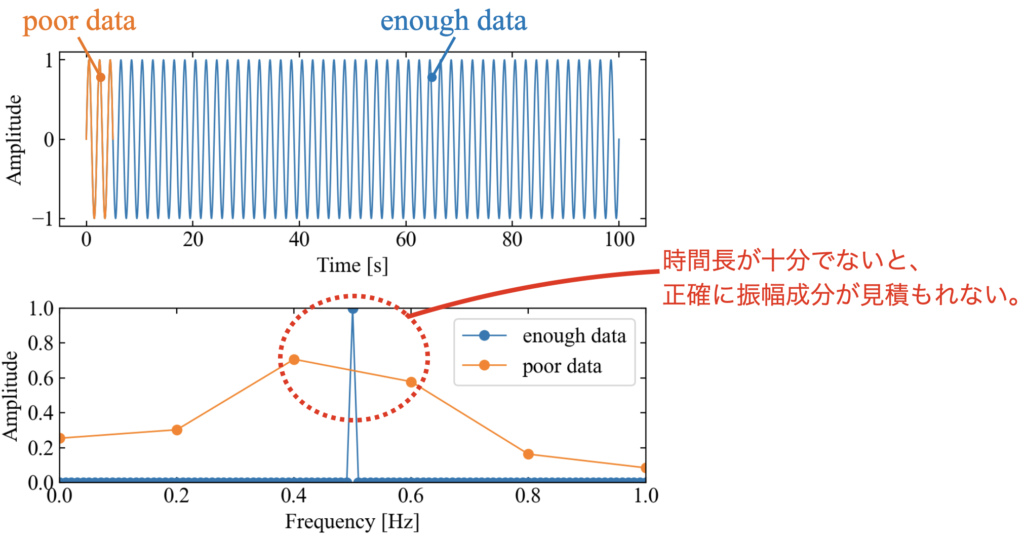
このように、着目しているピークが周波数分解能から漏れている場合は振幅成分が予想よりも小さくなってしまうので、周波数分析をする人は常に周波数分解能を気にする必要があると言えます。
止むを得ず周波数分解能が十分取れない場合
とりあえずフレーム周期を長くとっておけば良いんでしょ?簡単じゃん!
…と考えがちですが、止むを得ず周波数分解能を十分取れない場合はあります。
その一つが過渡現象です。例えば、ある制御されたモータがあって、分析したい回転数が一瞬で通り過ぎてしまう動かし方しか出来ない場合があるとしましょう。
このような実際の現象の振動等を計測する場合、得てして何秒も長い時間定常の現象を計測し続ける事は出来ません。
というわけで、十分な時間長のデータがいつも必ず揃うという事は無いと言えます。
無理やり周波数分解能を高める方法
ゼロパディングを使う
周波数分解能を高めるには、先ほどまでの検討の結果からフレーム周期を長くとれば良いとわかりました。
定常振動で長時間計測できないデータでも、無理やりパディングする事で時間は長くする事が出来ます。
パディングとは?
パディング(Padding)とは、プディングではありません。以前機械学習の学習をしていた時に学んだものでしたが、もとは画像処理の分野で使われていた技術です。データの周りにさらに配列を追加する事を言います。
下図は画像(青部分)に対してパディング(赤部分を追加)した結果です。
今回フーリエ変換するためのデータは波形ですので、以下のような1Dデータになります。この1Dデータにゼロパディングを施すという事は、dataの前後にゼロをあてがう事になります。
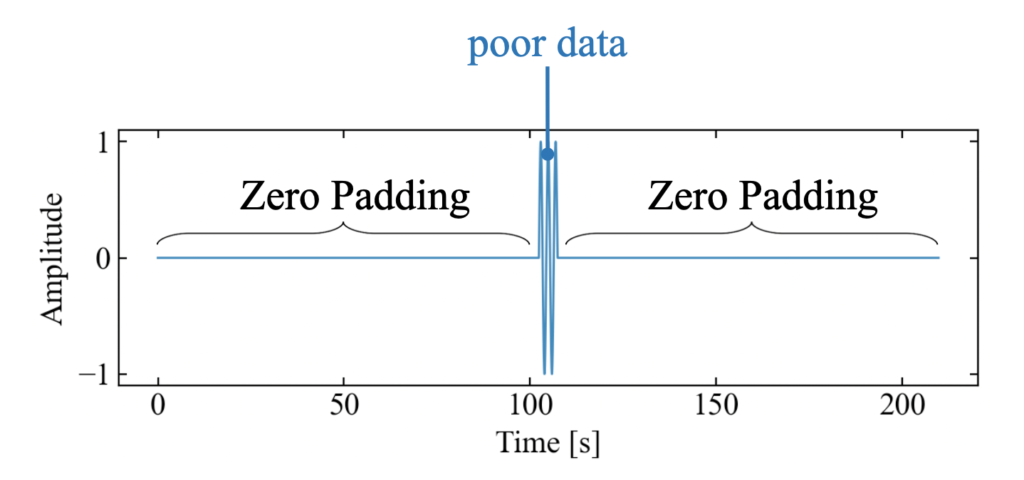
無理やりですが、これで見かけ上フレーム周期は長くなりました。
単純にゼロパディングすると振幅が変わる
以下はpoor dataにパディングのみを施した結果です。
ご覧の通り、緑色のpadding from poor dataはデータ点数は多くなっていますが、振幅は真値の1からずっと小さい値となってしまいました。
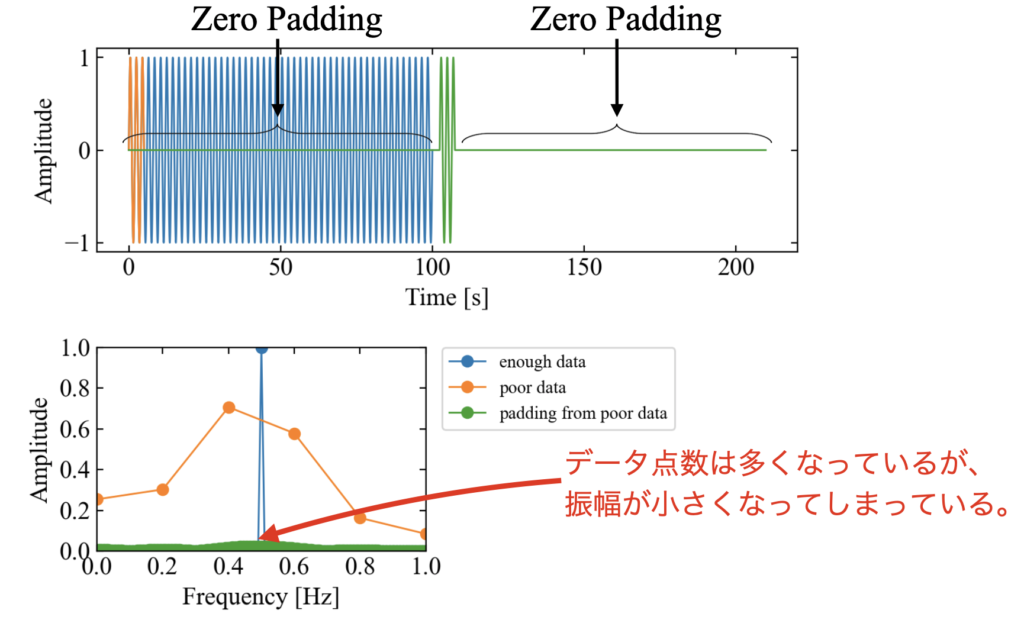
ずっと振動を繰り返す定常振動enough dataと比べ、パディング後のデータは一瞬しか振動していないので、当然ですね。エネルギー不足です。
振幅補正係数を使って改善する
振幅が小さくなってしまうのは、ゼロ配列を大量に追加したのに何も辻褄を合わせていないからです。
似たような現象に、FFTの時に使う窓関数の振幅補正係数があります。窓関数も元の信号を加工し、後で辻褄を合わせるように振幅を補正する処理を行います。詳しくは「窓関数使用時の補正!FFTの時に忘れがちな計算とは?」をご覧下さい。
今回は窓関数の時と異なり、時間長方向にデータを加工します。そのため振幅補正係数は以下のdef関数のacfで計算しました。この関数はパディングも一緒にやっています。
|
1 2 3 4 5 |
def zero_padding(data, len_pad): pad = np.zeros(len_pad) data_pad = np.hstack((np.insert(data, 0, pad), pad)) acf = (sum(np.abs(data)) / len(data)) / (sum(np.abs(data_pad)) / len(data_pad)) return data_pad * acf |
以下がゼロパディングと振幅補正係数の処理を共に行った結果です。
時間波形で見て振幅が小さくなった分を元に戻す処理をしています。
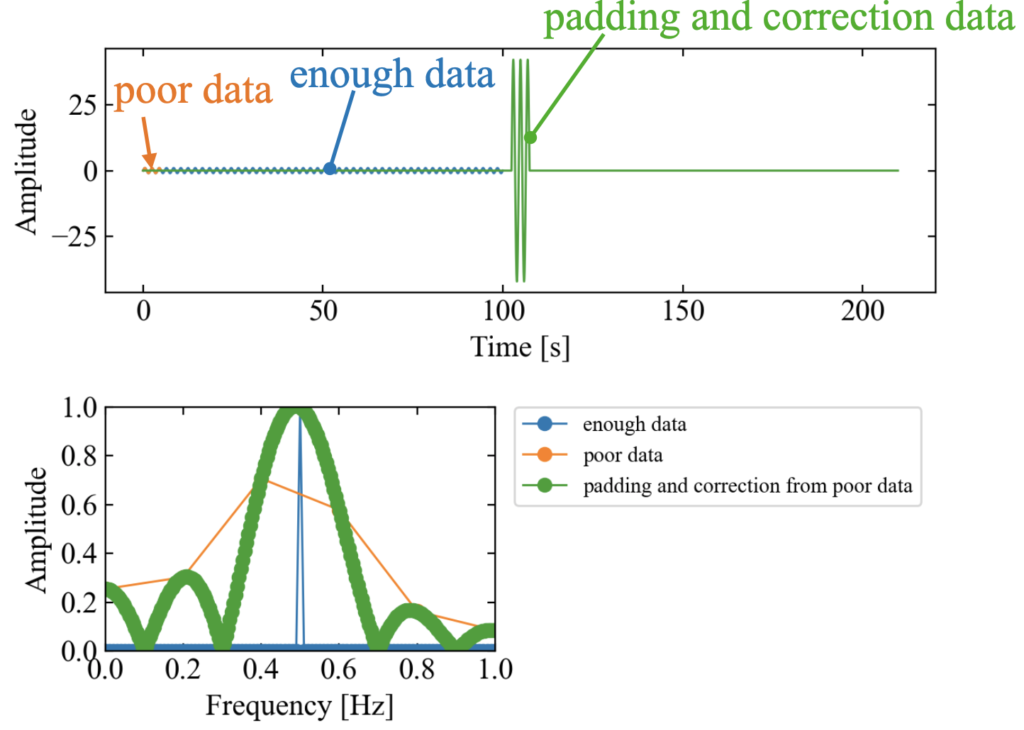
この結果はデータ点数が増え、さらに振幅も真値に近い結果を示しています。但し、信号自体の真の分解能が向上したわけではないという事に注意が必要です。
enough dataは周波数波形上で非常に鋭いピークとなっていますが、padding and correctionの方は幅の広いピークです。これは信号自体の情報はpoor dataと同じという事を意味しています。
FFTすると周波数分解能の増分値毎に一種の「ビン」にデータが入っているようなものです。そのためビンが真の周波数成分に合致していないと正しく振幅成分を表現する事ができません。
上記注意点はありますが、ちょっと分解能をいじる程度であればゼロパディングと振幅補正係数を使った加工は有効かも知れません。
ゼロパディングと振幅補正をするPythonコード
最後に今回のゼロパディングと振幅補正を使ってFFTを行う全コードを紹介します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt # フーリエ変換をする関数 def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成 return spectrum, amp, phase, freq def zero_padding(data, len_pad): pad = np.zeros(len_pad) data_pad = np.hstack((np.insert(data, 0, pad), pad)) acf = (sum(np.abs(data)) / len(data)) / (sum(np.abs(data_pad)) / len(data_pad)) return data_pad * acf samplerate = 2560 # サンプリング周波数 x = np.arange(0, 12800)/samplerate # 波形生成のための間軸の作成 data = np.sin(2 * np.pi * 0.5 * x) # 0.5Hzの正弦波を生成 # ゼロパディングした時間波形を生成 data1 = zero_padding(data, 2 ** 18) x1 = np.arange(0, len(data1)) / samplerate # 十分な長さを持った時間波形 x_theory = np.arange(0, 256000)/samplerate data_theory = np.sin(2 * np.pi * 0.5 * x_theory) # フーリエ変換を実行 spectrum, amp, phase, freq = calc_fft(data, samplerate) spectrum1, amp1, phase1, freq1 = calc_fft(data1, samplerate) spectrum_theory, amp_theory, phase_theory, freq_theory = calc_fft(data_theory, samplerate) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Amplitude') # スケールの設定をする。 ax2.set_xticks(np.arange(0, 2, 0.2)) ax2.set_xlim(0, 1) ax2.set_yticks(np.arange(0, 10, 0.2)) ax2.set_ylim(0, 1) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x_theory, data_theory, label='enough data', lw=1) ax1.plot(x, data, label='poor data', lw=1) ax1.plot(x1, data1, label='padding and correction from poor data', lw=1) ax2.plot(freq_theory, amp_theory, label='enough data', lw=1, marker='o') ax2.plot(freq, amp, label='poor data', lw=1, marker='o') ax2.plot(freq1, amp1, label='padding and correction from poor data', lw=1, marker='o') # レイアウト設定 fig.tight_layout() plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=10) # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
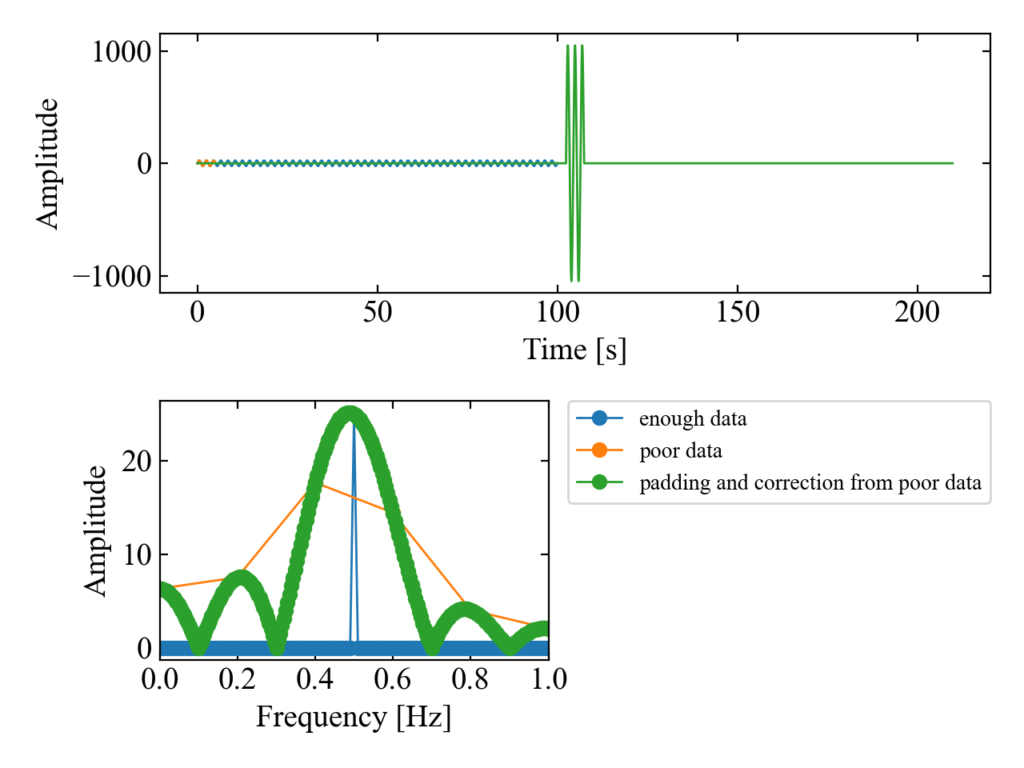
振幅を変化させても対応可能
おまけですが、先ほどは振幅1の信号でしたが、振幅を変更してもpoor dataからenough dataの振幅を再現するピークを得ることが出来ます。
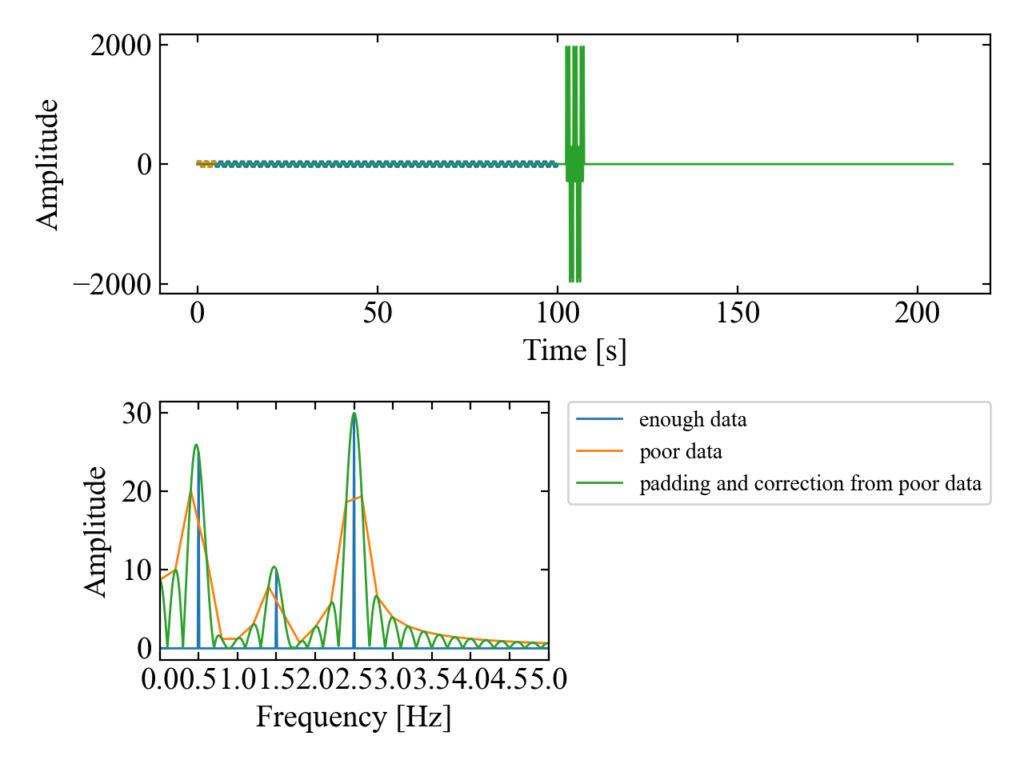
振動数を増やしても対応可能
複数振動数あってもpoor dataにゼロパディングと振幅補正を施した結果はenough dataの次数を再現しています(何度も言いますが、信号の分解能が上がったわけではなく、あくまでも周波数のビンを増やした程度の事しかしていません)。
まとめ
本記事ではちょっとしたデータ処理テクニックとして、計測データにゼロパディングを行う事で周波数分解能を向上させる方法を紹介しました。
しかしながら、ゼロパディングを行うだけだとFFT後の信号は振幅成分が小さくなってしまいます。
信号処理上これは不便なので、FFTで窓関数を使った時の振幅補正係数(Amplitude Correction Factor)と同様な考え方を使って振幅を補正する事を考えました。
これは周波数のビンの数を増やす事で、仮想的に周波数分解能を向上させているだけで、決して信号自体の分解能を向上させる魔法のコードでは無い事に注意して下さい。
本ページのコードは「MIT license(原文リンク)」に準拠しています。是非自由に使って下さい。
本日はいつもと違い、一風変わった処理として1Dの波形にゼロパディングを行う事で周波数分解能を向上させる方法をコーディングしてみました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!